中国、美国、德国初中数学教材中“勾股定理”比较研究

陈书才 (邮编:241000)

安徽师范大学附属萃文中学

董建功 (邮编:241000)

安徽师范大学数学与统计学院

2021年7月在中国上海举行的第14届国际数学教育大会(ICME-14)有一项小组专题研究,第41组(TSG41)主题是:数学学习和数学教材的资源研究与开发(www.icme14.net)．国际数学教材研究与发展会议(ICMT)已经举办三届,分别在英国南安普顿大学、巴西里约热内卢联邦大学、德国帕德博恩大学召开,2022年11月14日至17日第四届国际数学教材研究与发展会议(ICMT-4)在北京师范大学举行．

由Springer出版的《ZDM—Mathematics Education》(简称ZDM)是数学教育研究领域最权威的SSCI学术期刊之一,2013年9月第5期特刊包含11文章,主题是:Textbook research in mathematics education(数学教育中的教科书研究),2018年7月第5期特刊包含15篇文章,主题是:Recent advances in mathematics textbook and development(数学教科书的最新进展与发展),2021年10月第6期特刊包含17篇文章,主题是:Mathematics Textbooks as Instruments for Change(数学教材作为变革的工具).可见,数学教科书研究已成为国际数学教育研究的热点问题．范良火等(2013)列举了教科书分析比较研究中的五个最常见的主题:数学内容和主题;认知和教学法;性别、种族、公平、文化和价值问题;不同教科书的国际比较;概念和方法问题[1]．王建磐等(2018)研究了不同国家高中教科书中选择的内容和呈现方式[2]．王祎,范良火(2021)报道了一项实证研究,旨在通过比较的角度调查学生在上海和英国使用数学教科书的情况[3]．Sebastian Rezat,范良火和Birgit Pepin(2021)调查和分析了有关数学教材和课程资源作为变革数学内容[4]．王建磐、鲍建生(2014)做了五个国家高中数学教材中例题的综合难度的国际比较[5]．曹一鸣、吴立宝(2015)做了十个国家初中数学教材难易程度的国际比较研究[6]．吴立宝(2016)对初中数学教材的代数内容进行了国际比较研究[7]．付钰、张景斌(2018)进行了中美数学教材三角函数习题的比较研究[8]．覃淋(2019)进行了“中国大陆”“日本”和“中国台湾”高中数学教材统计习题难度比较研究[9]．胡典顺、王春静、王静(2020)进行了基于概念图的中外高中数学教材比较研究[10]．

上述研究拓展了视野,指出了教材研究的主题、研究方法等,为数学教材的比较研究提供了一般的方法和技巧,对教材研究提供了一个范式．在文献综述的基础上,发现大多数关于教材的研究立足于教材内容,从教科书的介绍,到分析知识点的安排、例题、习题设置、习题难度等．勾股定理(又称毕达哥拉斯定理)作为平面几何中最基础的定理,它是联系数学中数与形的第一定理,导致不可公度量的发现,揭示了无理数与有理数的区别,引发了第一次数学危机,勾股定理开始把数学由计算与测量的技术转变为论证与推理的科学[11]．鉴于勾股定理在平面几何中的重要的地位,所以有必要对最新的国际数学教材中“勾股定理”进行比较研究．希望本研究能对中国数学课程改革、数学教材编写、数学教育教学得到启发．

1 研究设计

1.1 研究文本的确定

中国选取人民教育出版社的数学教科书,人民教育出版社所出的数学教材在中国具有广泛的影响,用途较广．美国选取霍顿·米夫林出版社(Houghton Mifflin Harcourt Publishing)2020年出版的一套数学教材,霍顿·米夫林出版社是美国最具影响力的教育出版商之一,所出版的教材受众面较广．德国没有统一的教材,本研究选取的是由德国Klett出版社2021年出版的数学教材,该教材在巴伐利亚州广泛使用,巴伐利亚州位于德国南部,面积70550平方公里,约占德国国土面积的五分之一,是德国幅员最大的联邦州．三本样本教材详细信息见表1．

表1 样本教材基本信息

1.2 研究框架

结合“勾股定理”的具体内容,分别从单元整体结构、单元引入、例题分析、习题分析四个维度进行研究,具体研究框架见表2．

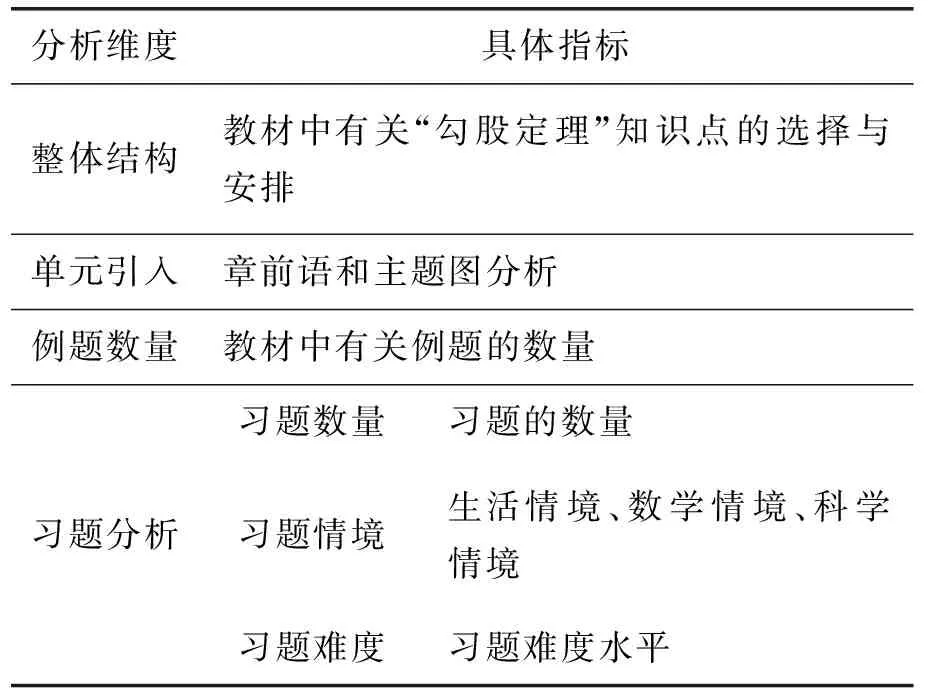
表2 研究框架

1.3 研究方法

本研究主要对中国、美国、德国三个版本初中数学教材中“勾股定理”进行比较研究,主要采用内容分析法和比较法等研究方法．习题难度测量模型参考了已有的研究[5-9],应用范围较广,并根据几何题目的特点主要从背景、推理、运算、知识含量4个难度因素进行比较,并对每个因素划分为3个水平,并分别赋值1、2、3．见表3.

表3 习题难度测量模型

各习题难度计算方法采用以下公式计算,其中:di表示第i个习题难度因素的加权平均值;i表示第i个习题难度因素;j表示某一个难度因素所处的水平;dij表示第i个难度因素的第j个水平上的权重;nij表示这组题目中属于第i个难度因素的第j个水平的题目的个数,其总和等于该组题目的总数n．

2 研究结果与分析

2.1 三个版本数学教材中“勾股定理”整体比较

整理分析三个版本数学教材中有关“勾股定理”章节的分布年级,单元页数和具体内容,详细信息见表4．

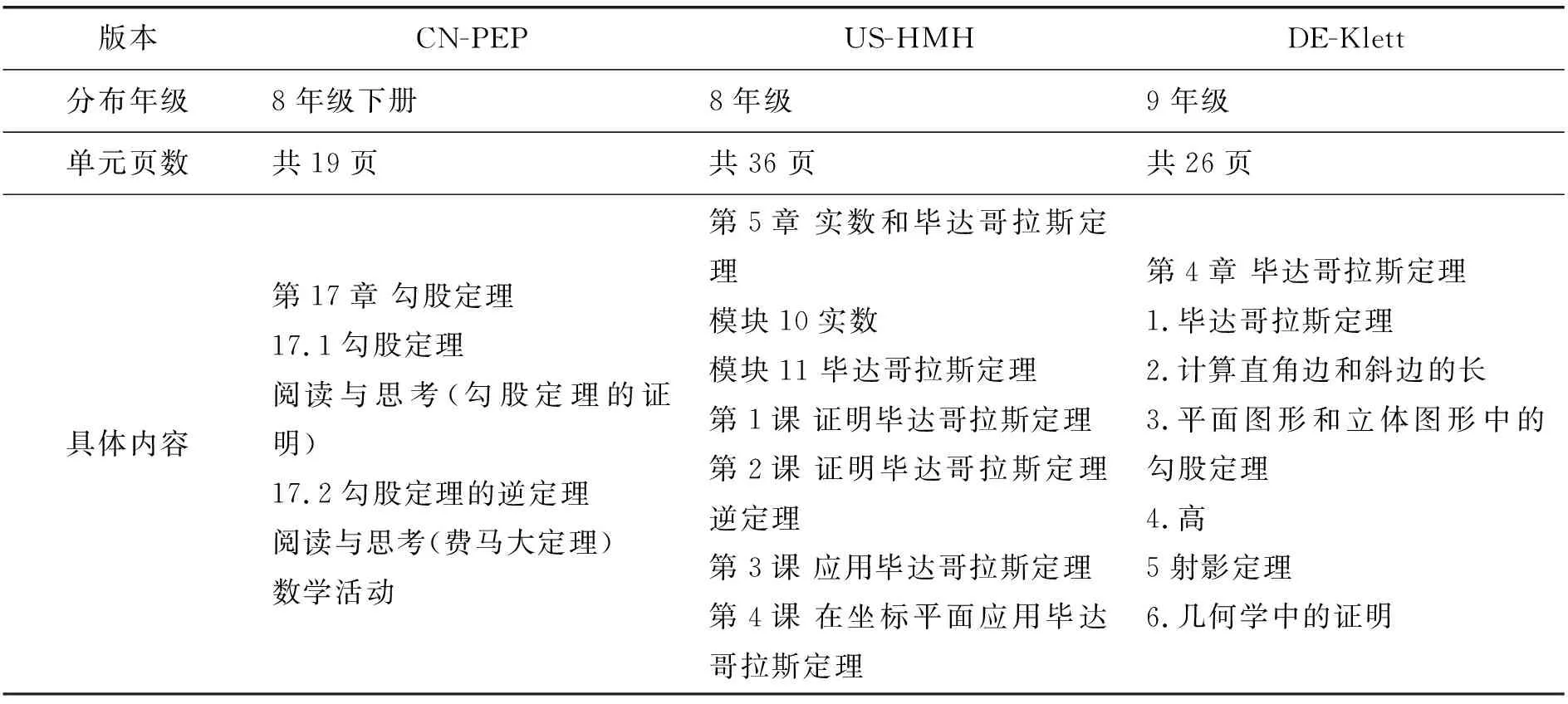
表4 “勾股定理”章节内容整体比较

对比分析表4可以看出,三个版本教材知识的编排顺序都体现了知识螺旋式的编排方式,都注重数学内容的整体性、关联性．但是三个版本教材在年级安排、内容选择等方面均有差异．CN-PEP版8年级下册安排了“勾股定理”,US-HMH版在8年级第5章安排了“毕达哥拉斯定理”,DE-Klett版在9年级第4章安排了“毕达哥拉斯定理”,通过比较发现,CN-PEP版安排了数学史知识和数学活动,说明CN-PEP教材不仅重视知识技能的培养,也重视人文科学的培养．

US-HMH版单独安排了一节在平面直角坐标系应用勾股定理,把“勾股定理”放在平面直角坐标系中去研究,并给出了距离公式．设两个点A、B的坐标分别为A(x1,y1)、B(x2,y2),则A和B两点之间的距离为:

两点之间的距离公式实际上是勾股定理的一个特殊形式,即当一个直角顶点坐标为(0,0)时,勾股定理的平方项可以简化为坐标差的平方和.说明US-HMH版教材注重几何和代数的联系,突出了勾股定理的距离意义,其内容广度更广．DE-Klett版安排了平面图形和立体图形中的勾股定理和射影定理.在解决平面图形中距离问题时,利用计算、平移、对称等方法,运用平面上两点之间线段最短的道理,构造直角三角形,进而利用勾股定理求解,在解决有关立体图形中路线最短的问题,把立体图形中的路线问题转化为平面上的路线问题,在平面图形中将路程转化为两点间的距离,然后借助直角三角形利用勾股定理求出最短距离．说明DE-Klett版注重知识之间前后的关联,注重几何思维和逻辑推理能力的培养,深化了勾股定理的距离意义,其内容广度更广,内容深度更深．

2.2 三个版本数学教材章首语和主题图

章首语即章节引入语,主要作用是激发学生学习探究新知识的兴趣．CN-PEP版(图1)介绍了中国古代数学书《周脾算经》一书上记载,在约公元前11世纪,人们就已经知道,如果勾是三、股是四,那么弦是五．后来人们进一步发现并证明了关于直角三角形三边之间的关系——两条直角边的平方和等于斜边的平方,这就是勾股定理．US-HMH版(图2)介绍了埃及的金字塔是在5000年前建造的,而建造它们的人是用数学来建造的,我们的知识在很大程度上归功于历史学家,我们研究过去的人、事件和思想,以及他们对当今世界的影响,历史学家利用他们收集的信息来发展理论,并对他们的主题进行总结．DE-Klett版(图3)介绍了古埃及的绳索拉紧器是十二结绳被十二个结分成十二条等长的绳子,第十二个结连接着绳子的起点和终点,据认为,古埃及的紧绳者在每年的洪水过后,用十二结绳来勘察田地,在建造寺庙时,这些绳索也可能被用来构建角度．通过对比发现三个数学版本的教材都是用数学史作为引入,帮助学生认识“勾股定理”在生活中的应用,引发学生探究勾股定理的欲望,有利于帮助学生体会数学的创造过程,从而培养学生正确的数学思维方式．

图1 CN-PEP

2.3 三个版本数学教材中例题数量

通过统计例题得到CN-PEP版共有4题,US-HMH版共有6题,DE-Klett版共有12题,如图4．通过分析可知DE-Klett版例题最多,US-HMH版例题次之,CN-PEP版例题最少．

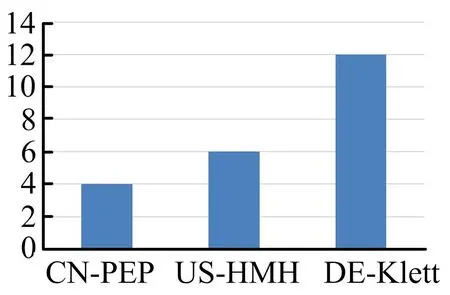
图4 三个版本数学教材中例题数量分析

2.4 三个版本数学教材习题难度分析

根据表3给出的习题难度测量模型,分为四个维度统计各个难度因素中各个水平的习题数量和百分比,统计结果如表5所示．

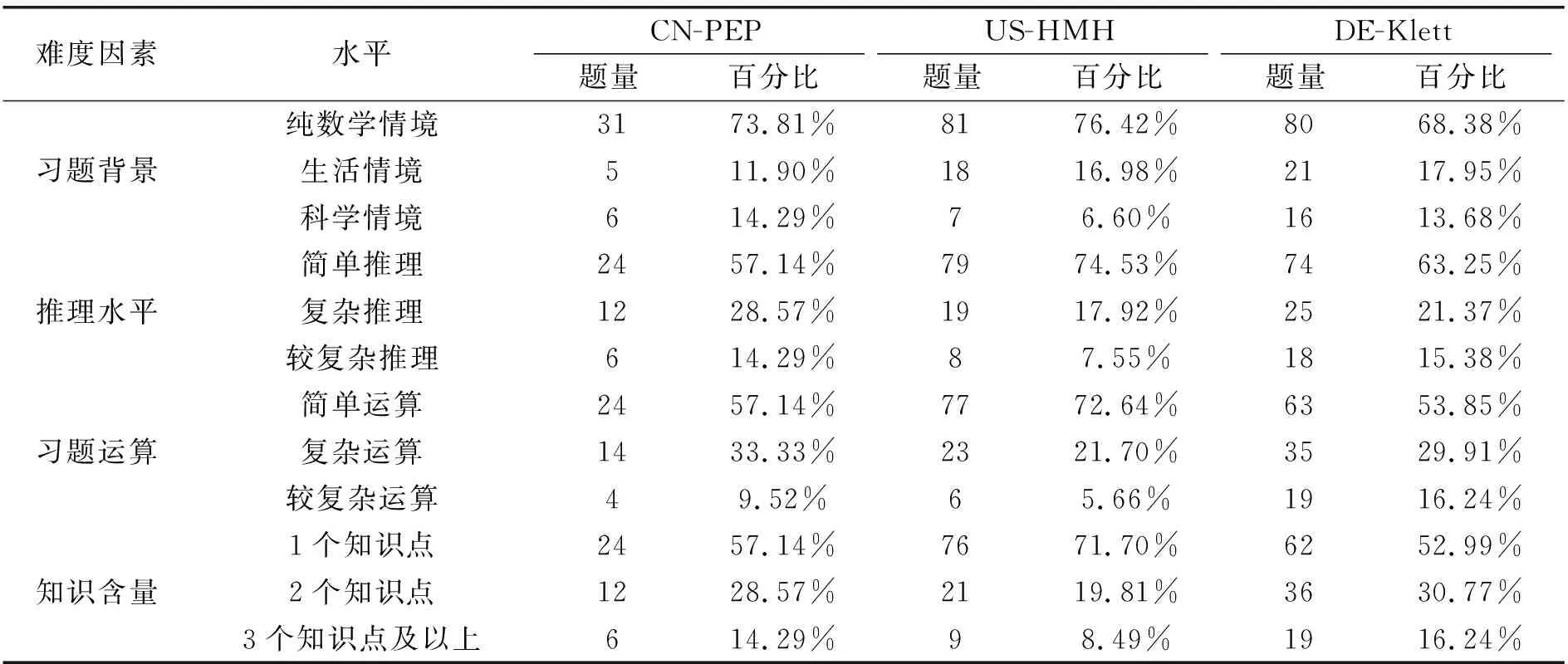
表5 三个版本数学教材难度因素比较

(1)习题背景

表5可知,三种数学教材中,“纯数学情境”的习题分别占73.81%、76.42%、68.38%,“生活情境”的习题分别占11.90%、16.98%、17.95%,“科学情境”的题目分别占14.29%、6.60%、13.68%．绘制折线图如图5所示.

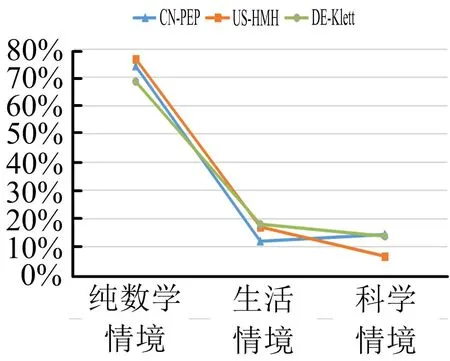
图5 三种数学教材在习题背景因素上的比较

纯数学情境,指纯粹数学问题表述;生活情境,指学生熟悉的生活中的现象和问题;科学情境,指涉及到科学知识和其他学科融合．通过图5发现三种版本数学教材中纯数学习题所占比例最大,都在百分之70左右．在生活情境上,DE-Klett版所占比例最多,其次是US-HMH版,最后是CN-PEP版．在科学情境上,CN-PEP版所占比例最多,其次是DE-Klett版,最后是US-HMH版．通过对比发现,三种教材纯数学情境最多,说明三种数学教材均重视基础知识和基本技能的培养;其次是生活情境,说明三个版本的教材均重视学生的生活经验,重视数学在生活中的应用,尤其是德国DE-Klett版教材提供了大量的生活情境的图片;最后是科学情境,说明三种数学教材均重视数学与其他学科的联系,值得一提的是US-HMH版教材每一节习题中都有一题或两题STEM(科学、技术、工程、数学)情境的题目．

(2)推理水平

由表5可知,三种数学教材中,“简单推理”的习题分别占57.14%、74.53%、63.25%,“复杂推理”的习题分别占28.57%、17.92%、21.37%,“较复杂推理”的题目分别占14.29%、7.55%、15.38%．绘制折线图如图6所示．

图6 三种数学教材在推理水平因素上的比较

推理的难易程度在一定程度上反映了教材的难易程度,通过图6发现,US-HMH版教材简单推理最多,其次是DE-Klett版,最后是CN-PEP版,在“复杂推理”水平上,CN-PEP版所占比例多于DE-Klett版,US-HMH版所占比例最少,在“较复杂推理”水平上,DE-Klett版所占比例最多,其次是CN-PEP版,最后是US-HMH版．

(3)习题背景

由表5可知,三种数学教材中,“简单运算”的习题分别占57.14%、72.64%、53.85%,“复杂运算”的习题分别占33.33%、21.70%、29.91%,“较复杂运算”的习题分别占9.52%、5.66%、16.24%．绘制折线图如图7所示．

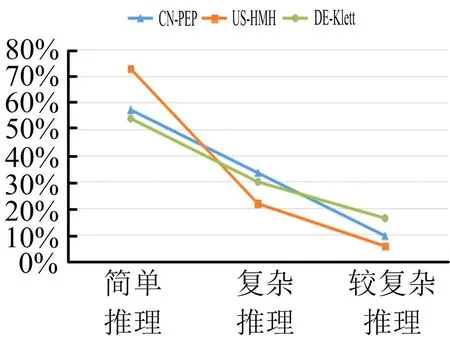
图7 三种数学教材在习题运算因素上的比较

运算能力是数学能力的重要组成部分之一,通过数学运算,学生可以巩固基本知识,提高解决实际问题的能力．通过图7发现,在“简单运算”水平上,US-HMH版教材所占比例最多,其次是CN-PEP版,最后是DE-Klett版;在“复杂运算”水平上,CN-PEP版教材所占比例最多,其次是DE-Klett版,最后是,US-HMH版;在“较复杂运算”水平上,DE-Klett版所占比例多与CN-PEP版多与US-HMH版．

(4)知识含量

由表5可知,三种数学教材中,“1个知识点”的习题分别占57.14%、71.70%、52.99%,“2个知识点”的习题分别占28.57%、19.81%、30.77%,“3个知识点及以上”的习题分别占14.29%、8.49%、16.24%．绘制折线图如图8所示．

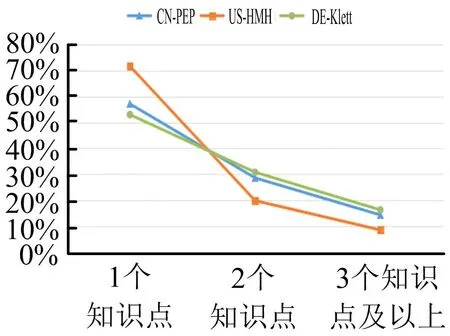
图8 三种数学教材在知识含量因素上的比较

通过图8发现,在“1个知识点”水平上,US-HMH版教材所占比例最多,其次是CN-PEP版,最后是DE-Klett版;在“2个知识点”水平上,DE-Klett版教材所占比例最多,其次是CN-PEP版,最后是US-HMH版;在“3个知识点及以上”水平上,DE-Klett版所占比例多于CN-PEP版多于US-HMH版．通过对比发现,US-HMH版教材偏重单个知识点的练习,DE-Klett版教材注重知识的综合性练习．

(5)综合难度

在对习题难度的4个因素进行比较分析的基础上,根据习题综合难度测量模型,对各难度因素进行加权平均值计算得到表6．

为了更加直观呈现得到的结果,绘制雷达图,如图9．

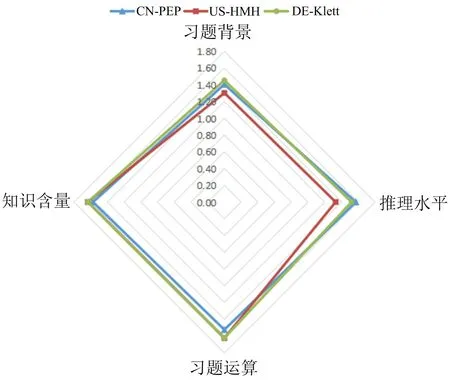
图9 三种数学教材习题综合难度直观模型

从“习题背景”上看,DE-Klett版大于CN-PEP版大于US-HMH版,从“推理水平”上CN-PEP版大于DE-Klett版大于US-HMH版,从“习题运算”和“知识含量”上看,DE-Klett版和US-HMH都大于CN-PEP版,最后从“综合难度”上看,DE-Klett版大于CN-PEP版大于US-HMH版．

3 研究结论

三种版本数学教材“勾股定理”编写既有相同之处,也有不同之处,相同之处表现在:

(1)在内容选择上,三种版本教材虽然标题或名称不同,但都包括勾股定理,勾股定理逆定理基本知识点,在章节引入上,三种数学教材都使用了数学史素材．(2)在内容组织上,三种版本教材都采用了“螺旋式”编写特点,都注重数学内容的整体性、联系性.(3)在习题情境上,三个版本数学教材纯数学情境所占比例最多,都重视注重问题情景和数学活动,提供大量的生活情境,强调数学与现实生活的关系．

三种版本数学教材“勾股定理”编写存在着一定的差异,其差异性表现在:

(1)在内容选择上,美国版数学教材安排了“在平面直角坐标系中应用勾股定理”,其内容广度更广．德国版数学教材涉及知识点比较广,其内容广度更广且内容深度更深,例如安排了“在平面图形和立体图形中应该勾股定理”和“射影定理”等内容．美国版教材和德国版教材都注重突出勾股定理的距离意义．

(2)在习题难度上,首先从“综合难度”上看,德国数学教材习题难度最高,其次是人教版数学教材,最后是美国数学教材;从“习题背景”上看,德国数学教材大于人教版大于美国版;从“推理水平”上人教版数学教材大于德国数学教材大于美国数学教材;从“习题运算”和“知识含量”上看上,德国和美国数学教材都大于人教版数学教材．另外,值得一提的是美国版数学教材和德国版数学教材在教材最后都提供了练习题参考答案,人教版数学教材没有习题参考答案．

4 启示

它山之石可以攻玉,通过以上的分析,结合中国、美国、德国数学教材的特点,提出几点对中国数学教材编写的建议．

4.1 注重数学知识之间的联系

通过比较分析发现三种版本数学教材都体现教材编写的知识之间螺旋上升的特点,美国教材和德国教材在知识的内容选择上,内容广度更广,内容深度更深,尤其是德国数学教材,以“勾股定理”为例,把和“勾股定理”有关的知识点几乎都联系起来了．美国版教材和德国版教材都注重突出勾股定理的距离意义．教材编写要体现知识之间的关联,将知识点按照一定的逻辑进行排序、整合,形成相互联系、易于理解和迁移的知识结构,体现知识内容的整体性和关联性,体现大单元思想和知识的结构化特征．

4.2 注重真实问题情境的设置

PISA 2021把数学素养表述为:数学素养是个人在不同真实世界情境下进行数学推理并表示、使用和解释数学来解决问题的能力[12]．三个版本教材都使用了大量的情境,都体现了数学与现实生活的联系,以德国数学教材为例,不仅提供了大量的生活情境而且提供了一些科学情境,且教材情境图片选择真实、精美,与学生生活息息相关．在教材编写过程中应注重真实情境的设置,提高学生在真实复杂情境中解决问题的能力,进一步提高学生的数学核心素养．

4.3 注重与信息技术的结合

信息技术最重要的价值之一就是变革数学教学模式,使得数学探究、数学实验和数学建模等更加可操作[13]．以图形计算器为例,信息技术支持下数学建模的教学不再局限于课堂,不再停留在虚拟的情境中．借助图形计算器技术,学生可以直接在真实的生活情境和科学情境中收集数据、分析数据、构建模型并检验模型．在教材编写时,不仅要体现计算工具的使用,也要体现图形工具和软件在数学中的应用,作图软件的应用可以更加直观和精确地体现几何图形的特征,帮助学生增强学生的几何直观能力,发展学生空间想象能力和几何逻辑推理证明能力,提高学生数学建模的能力．

4.4 注重与其他学科的融合

重视学科的交叉与融合,不仅是教育发展的必然趋势,也是数学现代发展的时代特点,世界上许多国家都重视数学教科书中的跨学科内容研究[14]．通过研究发现美国教材在习题设置上体现了STEM理念,专门设置了STEM题目．在教材编写的过程中,体现跨学科的特征,不仅重视对自身学科的理解,也要注重学科之间的关联和整合,以数学课程内容为基础,运用并整合其他学科知识,探究和解决社会生活和科学技术问题,提高学生应用数学的能力．