地铁车站步行障碍行人避让行为建模与进出站仿真

郝妍熙，卫书彤，胡华，王润祺，刘志钢

(上海工程技术大学，城市轨道交通学院，上海 201620)

0 引言

“十四五”时期，我国人口老龄化程度将进一步加深，60 岁及以上人口占总人口比例将超过20%，进入中度老龄化社会[1]。同时，我国残疾人数量已超过8500万人，3岁以下婴幼儿已达4200万人。由于空间条件和行动能力的限制，助老、助残、助幼出行行人及携带重物行人等会表现出异于普通行人的微观出行行为。《无障碍环境建设法》的通过[2]切实保障步行障碍行人群体出行权益，因此为向步行障碍行人提供更精细化的出行服务，需研究步行障碍行人的微观行为。

目前，微观行人仿真模型主要有社会力模型、元胞自动机模型等。元胞自动机模型是一种时间、空间和状态都离散化的网格动力学模型。Blue等[3]最早将元胞自动机模型应用到行人仿真中，让相邻单元格的状态来决定行人每个时间步的移动方向；Gao等[4]考虑到人群非理性决策因素，将累积前景理论(CPT)与元胞自动机模型相结合(CPT-CA)模拟出更接近实际的出口选择和路径选择行为。

许多学者也考虑到行人个体间的差异性对行人流进行了广泛研究。吴昊灵等[5]将行人划分为结伴行人、快速行人和普通行人这3 类，构建改进场域模型对地铁站楼梯通行能力进行研究；Li等[6]提出一种改进元胞自动机模型研究高铁站台乘客上车过程中携带行李乘客对车站拥挤程度及上车效率的影响；李永行等[7]将行人分为领导者和追随者，将情绪传播模型、领导者—追随者模型和出口选择策略融合到基于元胞自动机模型的行人仿真模型中，模拟了多出口情况下的疏散过程。

此外，也有学者研究了行人的避让行为。马尚等[8]引入主动避让力的改进社会力模型，还原对向行人间的避让行为；霍非舟等[9]建立考虑主动避让弱势群体的元胞自动机模型，通过规定3种避让方式探究主动避让行为对养老场所人员疏散的影响；陈鹏等[10]在研究无信控路段人行横道处行人过街行为时，引入行人主动避让力改进社会力模型。

综上，目前较少有研究涉及步行障碍行人与普通行人之间冲突避让机理。因此，本文旨在建立考虑步行障碍行人运动特性的元胞自动机模型，分析步行障碍行人的微观出行特性和避让行为规律，为确保行人交通流的安全和效率以及设计更安全合理的行人交通基础设施提供依据。

1 步行障碍行人元胞自动机建模

1.1 步行障碍行人

由于个体属性的不同，行人间会产生空间需求、身体状况、结伴状况、携带重物状况等生理性差异，以及性格、个体紧张程度、对环境熟悉程度等心理性差异。步行障碍行人指的是在行人交通流中，由于年龄、身体状况或携带重物等因素面临行动上的挑战，需要更多时间、空间或他人结伴辅助才能进行出行的行人群体。本文研究的步行障碍行人包括轮椅行人、婴儿车行人和携带重物行人。

1.2 考虑步行障碍行人的元胞自动机模型改进

1.2.1 行人空间划分

在离散的二维元胞空间内，根据人群中典型的行人物理尺寸，将每个单元格的尺寸设置为0.4 m×0.4 m。根据摩尔邻域规则对行人元胞周围的8 个单元重新定义，扩展基本场域以建立步行障碍行人场域。在模型中设置4 类人员：普通行人、轮椅及婴儿车行人、携带重物行人，分别对应图1(a)～图1(c)所示的3 种元胞邻域，空间内每个元胞可以被一名行人、一座轮椅、一辆婴儿车或一件重物占据，也可以为空[8]，轮椅和婴儿车元胞位于行人元胞运动方向的正前方，而重物元胞分布在行人元胞周围的8 个相邻元胞之一，图1(d)提供了重物元胞位置的示例。

图1 步行障碍行人场域图及重物可能被携带位置示例Fig.1 Mobility-impaired pedestrians zone map and examples of possible locations for heavy objects

1.2.2 行人及物品更新规则

(1)模拟行人更新规则

Step 1 初始化场景，计算静态场S 和动态场D。

Step 2 判断是否所有行人都出现于场景中。若否，转至Step 1。

Step 3 在每个时间步中，首先更新动态场D，然后根据乘客顺序更新所有乘客的位置。根据第p名乘客的速度Vp与最大速度比值确定第p名乘客是否可以移动，并根据行人转移概率更新位置。

Step 4 判断是否所有乘客都已疏散完毕。若是，则停止模拟；否则，返回Step 2。

(2)步行障碍行人物品相对位置调整规则

Step 1 根据行人转移概率确定下一时间步中步行障碍行人位置(xnext,ynext)与其物品初始目标元胞(x+itemp,y+jtemp)。其中，itemp与jtemp表示步行障碍行人物品对于步行障碍行人当前位置的相对偏移量，步行障碍行人物品在下一时间步骤中占用的空间在Step 1中不考虑。

Step 2 观察Step 1 中初始目标元胞周围map_people，判断行人是否可以如图1 的空间结构携带物品移动到此单元。若是，转至Step 3；否则，行人无法在下一时间步骤中移动并转至Step 4。

Step 3 检查行人是否能在下一时间步保持原有的空间结构。若是，移动到下一时间步；否则，行人停止移动，转至Step 4。

Step 4 更新行人及其辅助物位置。

(3)行人冲突处理规则

由于模型并行更新规则，当两个或多个行人将在同一时间步中转移至同一元胞，就会发生冲突。本文将冲突分为水平对向冲突与非水平对向冲突，如图2所示。

图2 行人冲突示意图Fig.2 Pedestrian conflict diagram example

普通行人间、步行障碍行人间、普通行人与步行障碍行人间皆会发生冲突，他们之间的冲突处理规则如下：

Step 1 引入竞争系数∂，规定普通行人竞争系数大于步行障碍行人竞争系数；并判断冲突类型，水平对向冲突转至Step 2，非水平对向冲突转至Step 4。

Step 2 判断各冲突行人运动方向右方是否存在空元胞。若是，转至Step 3；否则，转至Step 4

Step 3 检查各行人运动方向右方均存在空元胞。

Step 3.1 若均存在空元胞，比较各行人∂大小，∂大的行人移动至右方空元胞，另一行人移动至目标位置；若∂相等，随机选择一行人移动至右方空元胞，另一行人移动至目标位置。

Step 3.2 若不都存在空元胞，右方存在空元胞的行人向右移动，另一行人移动至目标位置。

Step 4 比较各行人∂大小，∂大的行人移动至目标位置；若∂相等，则随机选择任一行人移动至目标位置。

1.2.3 行人运动及路径选择

场强模型用于确定行人的具体运动规则，得到行人移动的概率、方向等基本参数，基础场强模型包括静态场与动态场。所有行人在每个时间步有9个移动选项，用表示选择目的地n的行人向元胞(i,j)的转移概率，即

式中：N为归一化因子，以确保和为动态场和静态场的值；kd、ks为灵敏度参数，kd反映行人从众趋势，ks衡量行人对建筑结构的熟悉程度；μij为相邻单元(i,j)占用状态，若被占用为1，否则为0；ξij为与障碍物有关的0-1变量，若存在障碍物导致相邻单元不可达则为0，否则为1。

由于行人普遍存在从众心理，利用动态场Dij来描述人群朝着目的地前进时行人间的作用力，可设置为元胞(i,j)相邻8 个单元中的空单元格数。首先定义行人间作用力的范围为一个3×3 的摩尔面积，结合行人间速度方向把每一步的速度作为一个向量累加以增强行人的转移趋势。

每个行人都有向目的地移动的倾向，利用静态场描述行人与目的地间的最短距离，对目的地行人间的吸引力进行量化，即

式中：为元胞(i,j)到第n个目的地的势能；为元胞(i,j)相邻单元到目的地n势能的最大值；Oij为元胞(i,j)的相邻单元中非障碍物占用的数量；kL、ko为加权参数。

本文采用Breadth-first Search Algorithm(BFS)计算每个元胞的势能。根据相邻单元是否在对角线上，将其分成两部分。在势能的第1 次分配中，给目的地冯诺依曼邻域内元胞的势能取值1.0，给目标位置对角线上的元胞势能取值1.4，如图3所示。

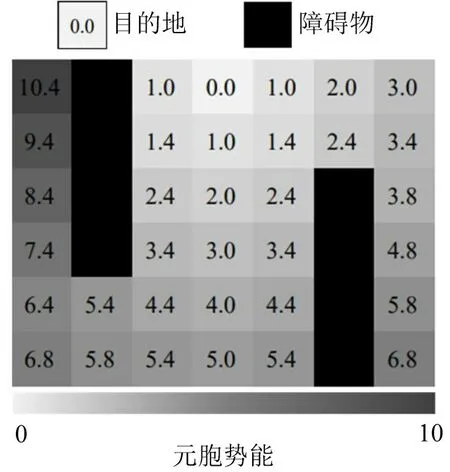
图3 元胞势能计算图例Fig.3 Example of a cell potential energy calculation

本文行人运动的特征通过两个基本参数来描述，即速度v和行人密度ρ，其关系可用Kladek 公式[11]描述，即

式中：vM为普通行人的平均自由速度，vM=1.2 m·s-1；γ为行人对于不同场景的敏感指数，取值范围为(1,3)；ρM为堵塞密度，计算公式为

式中：Sm为行人的平均占地面积，根据单元格尺寸设置本文取0.16 m2；βG为亚洲国家地理面积系数，本文取0.847[11]。

式(5)与场强模型相结合，共同影响行人的路径选择行为。静态场涵盖了目标位置和障碍物等关键信息，通过设置目标位置和障碍物的势能，行人在路径选择中倾向于避开障碍物且选择通向目标位置的路径。动态场信息以势能的形式嵌入到模型的更新规则中，行人在路径选择时，通过评估当前位置的动态场势能，更倾向于选择相对势能较低的区域。Kladek 公式描述了行人速度v和行人密度ρ之间的关系，行人密度的变化会影响速度。行人根据计算得到的速度和动态场势能来选择下一个目标元胞，他们更趋向于选择速度较快、势能较低的路径。这种综合了静态场、动态场以及速度—密度关系的模型使路径选择规则更为复杂、细致，能够更好地模拟拥挤情况下的疏散行为。

1.2.4 模型更新规则

对于二维的元胞自动机模型，其可行距离仅为几何距离，当平面上存在障碍物或复杂结构时，设定的模拟行人无法通过。结合上述模型与Huang等[12]开发的距离矩阵通过以下步骤计算行人的运动过程。

Step 1 检查所有单元，若单元(i,j)未被障碍物占用，则元胞单元的势能0，单元格占用指标0；否则

Step 2令k=，检查所有单元格。

Step 2.1 当单元(i,j)在目的地摩尔邻域内且满足0 时，若单元(i,j)与目的地呈冯诺依曼相邻关系，令1；若单元(i,j)与目的地呈对角关系，则2。

Step 2.2 当单元(i,j)在其相邻单元(i0,j0)摩尔邻域内且，0 时，若单元(i,j)与单元(i0,j0)呈冯诺依曼相邻关系，令1；若单元(i,j)与其相邻单元(i0,j0)满足对角关系，则

Step 2.3若≠0 适用于所有单元格，转至Step 3；否则，检查0 单元与其周围单元及目的地的位置，令k←k+k1或k←k+k2并转至Step 2.2。

Step 3令k=1，检查所有单元格。

Step 3.1 当单元(i,j)在目的地摩尔邻域内且满足0 时，令。

Step 3.2 当单元(i,j)在其相邻单元(i0,j0)摩尔邻域内且，0 时，令1。

Step 3.3若≠0 适用于所有单元格，转至Step 4；否则，检查0 单元，令k←k+1 并转至Step 3.2。

Step 4 对于每个单元(i,j)，计算其距离矩阵ε为影响出口附近人群分布状态，此处将其设置为-1[6]。

结合式(1)和式(4)可将行人转移概率表示为

式(7)中，由于与为负相关，与Oij、Dij呈正相关关系，因此有k1<0，k2、k3>0。本文将这3个参数定义为k1=-5、k2=1、k3=1[13]。

2 步行障碍行人运动场地实验及模型参数标定

2.1 实验及数据

本文选取一条长22.5 m、宽5 m 的直通道进行试验，如图4所示。在直通道正上方30 m处放置视频分辨率为1920×1080、帧率为30 frame·s-1的无人机作为实验记录设备。

图4 实验场地平面图Fig.4 Plan of experimental site

实验招募不同身高、体重的11 名年龄范围在[18,53]岁的志愿者(男性6人，女性5人)。其中，步行障碍行人主要分为轮椅行人与婴儿车行人，各实验行人示意图如图5所示，实验设置如下。

图5 实验中行人示意图Fig.5 Illustration of pedestrian in experiment

(1)1名步行障碍行人+1名普通行人(单—单对向冲突)；

(2)1名步行障碍行人+7名普通行人(单—多对向冲突)；

(3)2名步行障碍行人+7名普通行人(二—多对向冲突)。

在直通道内总共进行60 组试验，包括轮椅行人与婴儿车行人各10 组的单—单对向冲突场景、单—多对向冲突场景以及二—多对向冲突场景。通过多次重复试验，旨在获取尽可能多的行人走行与冲突避让情况，以提高行人运动及冲突参数的准确性。

对每组实验行人轨迹进行标定，得到每位实验者的时间、坐标及速度等数据，数据示例如表1所示。

表1 实验数据提取字段示例Table 1 Example of experimental data extraction fields

2.2 数据分析

避让行为是对向行人流中常见的现象，为了定量分析轮椅行人、婴儿车行人与其前方普通行人冲突的差异，采用偏移角度α、横向移动距离进行比较。横向移动距离分为横向相对距离Δy与横向偏移距离Δys。如图6所示，横向相对距离Δy指普通行人与步行障碍行人在t时刻y轴坐标的差值，Δx指普通行人与步行障碍行人在t时刻x轴坐标的差值。横向偏移距离指行人在单位时间内朝y轴方向偏移的距离。

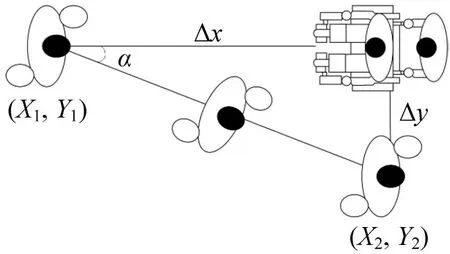
图6 行人偏移角度及相对距离图示Fig.6 Illustration of pedestrian offset angle and relative distance

式中：α为偏移角度；Δy为横向相对距离；Δys为横向偏移距离；X1、X2为行人1、2的横坐标值；Y1、Y2为行人1、2的纵坐标值；1、2、N为行人编号；YN,t为t时刻编号N行人纵坐标值；YI,t为t时刻步行障碍行人I纵坐标值。

根据实验行人数据及式(8)～式(10)，计算出普通行人与步行障碍行人的偏移角度、横向相对距离以及行人各自的横向偏移距离，如表2所示。

表2 实验行人避让冲突概况Table 2 Experimeweital pedestrian avoidance conflict profile

图7为普通行人、轮椅行人及婴儿车行人横向偏移距离箱线对比图，结合表2的具体数值可以发现，无论是轮椅行人或婴儿车行人，偏移角度与横向偏移距离基本相似，其在冲突避让过程中偏移角度和偏移距离均明显小于普通行人，这主要因为步行障碍行人运动能力小于普通行人，自由度较低。

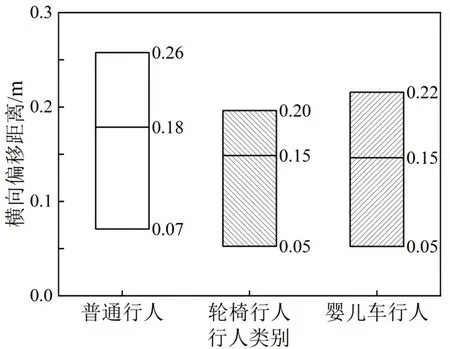
图7 行人横向偏移距离箱线图Fig.7 Boxplot of pedestrian lateral offset distance

同时，本文选取1组通道行人冲突避让实验的速度—轨迹图，如图8所示，可以发现，轮椅行人的瞬时速度小于其前方的普通行人，普通行人在感知到前方存在步行障碍行人时，会提前加速避让，进而使得速度—轨迹图中普通行人与步行障碍行人的行走轨迹与速度出现明显差异。

图8 通道行人冲突避让过程速度—轨迹图Fig.8 Velocity-trajectory plot of pedestrian conflict avoidance process in a corridor

2.3 模型验证

通过对比仿真与实验行人速度及行人横向偏移距离，从定量角度对所建模型进行验证。将2.4 m×22.4 m的仿真场景离散为6×56个元胞，每个元胞的尺寸为0.4 m×0.4 m。由实测数据可知，普通行人的期望速度为1.47 m·s-1，轮椅行人为1.15 m·s-1，婴儿车行人为1.20 m·s-1。每个时间步对应实际时间为0.1 s。共仿真6000 个时间步，前5000 时间步不计入结果统计，采用周期性边界条件。参数设定kS=4，kD=1，α=0.1，δ=0.4[5]，输入的行人仿真参数如表3所示。

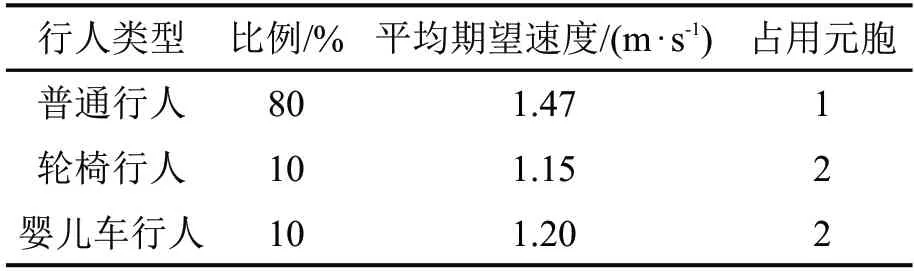
表3 模型参数汇总表Table 3 Summary table of model parameters

图9 为步行障碍行人冲突避让行为仿真过程。图10(a)速度箱线图结果显示，仿真行人平均速度为1.50 m·s-1，相较于实验行人平均速度1.46 m·s-1存在的误差为2.74%；且仿真行人速度方差为0.031，小于实验行人速度方差0.074。图10(b)中行人横向偏移距离仿真与实验的对比结果表明，普通行人在仿真中的平均横向偏移距离为0.185 m，与实验中普通行人的平均横向偏移距离0.179 m相比存在3.35%的误差；轮椅行人和婴儿车行人的仿真平均横向偏移距离与实验数据相比分别产生了6.71%和6.16%的误差。同时，普通行人实验与仿真横向偏移距离方差均为0.02，轮椅行人实验与仿真横向偏移距离方差分别为0.021、0.012，婴儿车行人实验与仿真横向偏移距离方差分别为0.014、0.012。

图9 步行障碍行人冲突避让仿真过程Fig.9 Simulation process diagram

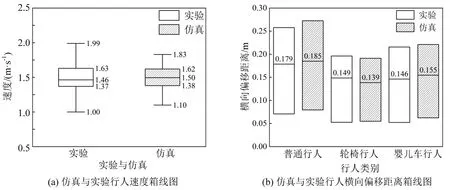
图10 仿真模型行人速度与横向偏移距离验证Fig.10 Simulation model validation of pedestrian speed and lateral offset distance

3 仿真案例分析

3.1 客流数据采集

仿真选取上海地铁11 号线迪士尼站站台层乘客出站场景，对到站客流类型比例数据进行采集。视频采集站台早高峰与平峰不同时段各8 次列车到站乘客出站场景，普通行人、轮椅行人、婴儿车行人、携带重物行人平均到站客流类型比例分别为86.50%、0.88%、9.25%、3.38%。

3.2 仿真参数设置

迪士尼地铁站是上海地铁11 号线南端终点站，其站台层平面分布如图11所示，迪士尼车站进出站客流呈现明显的潮汐现象，极少出现上下行站台同时排队的情况，因此仅考虑单列车到达的场景。仿真参数设置如下。

图11 站台层平面图Fig.11 Platform level plan

(1)仿真场景依据实际迪士尼站站台层尺寸，为一个144 m×20 m的矩形，包含列车停靠区域；设有8个出口(2部无障碍电梯、4个扶梯出口和2个楼梯出口)；无障碍电梯在单次运行中最多容纳12 名乘客，队列设置为单队列。

(2)每个元胞尺寸为0.4 m×0.4 m；行人时间步设置为0.1 s，即每0.1 s 更新一次，行人可以移动一个单位元胞。

(3) 列车中所有行人的初始位置均为随机分布；某节假日，迪士尼站平均到达客流为350人，故仿真平均到站人数设置为350人。

(4) 无障碍电梯上下客停留时间设置为10 s，上/下一层楼所需时间设置为5 s[14]。

(5)根据实测数据，行人在站台通道与楼扶梯处的速度不同，行人及设施参数汇总于表4和表5。

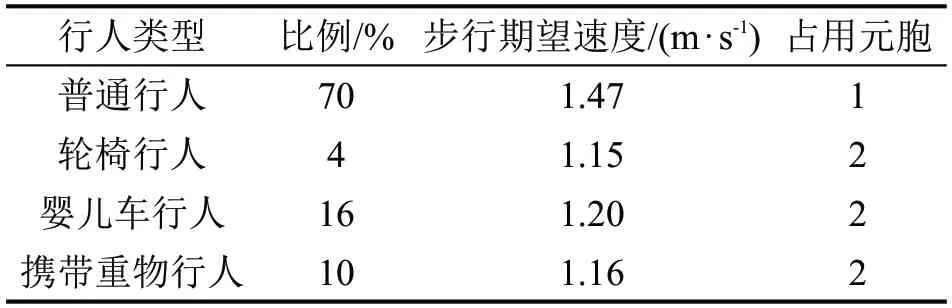
表4 行人参数汇总表Table 4 Summary table of pedestrian parameters

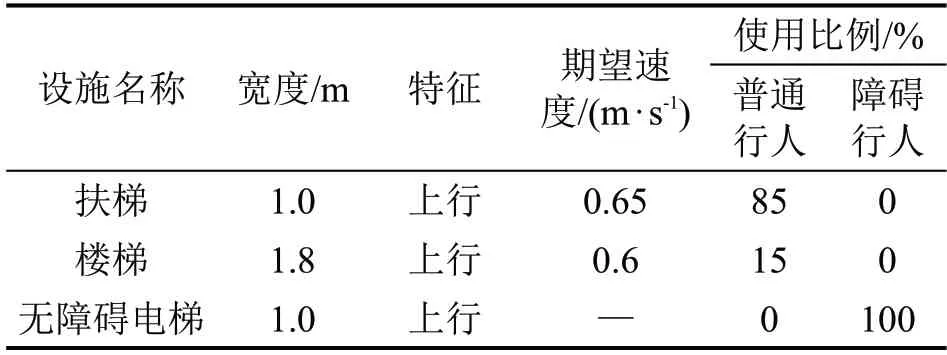
表5 迪士尼站台设施参数汇总表Table 5 Summary of facility parameters for Disney Station buildings

3.3 仿真结果验证

验证仿真过程中各行人运动状态的稳定性。通过10 次重复仿真实验，获得站台行人的出站时间在(235±3)s 范围内波动。10 次仿真实验的出站时间均值为234.7 s，标准差为1.79。与实际调查迪士尼站乘客出站时间(车厢人数为350 人)235 s 的结果进行对比，相对误差为0.1%，仿真实验结果稳定有效。图12 分别给出地铁站台候车通道、楼扶梯、无障碍电梯服务范围不同时间下仿真行人密度分布。

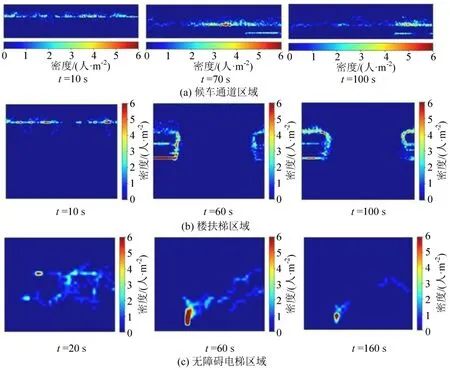
图12 仿真密度时间分布图Fig.12 Simulation density time distribution plot

为深入验证模型的适用性，在保持其他仿真参数不变的情况下，设置3 种不同的列车到站客流量，即350，700，1050人，并进行相应的仿真，3种客流下的疏散时间分别为235，465，703 s。不同到站客流下行人疏散累计密度分布如图13 所示，随着到站客流量的增加，行人高密度区域不断扩展，乘客疏散行人流的状态与实际情况相符，进一步验证了本文构建的模型在不同客流密度下的稳定性。

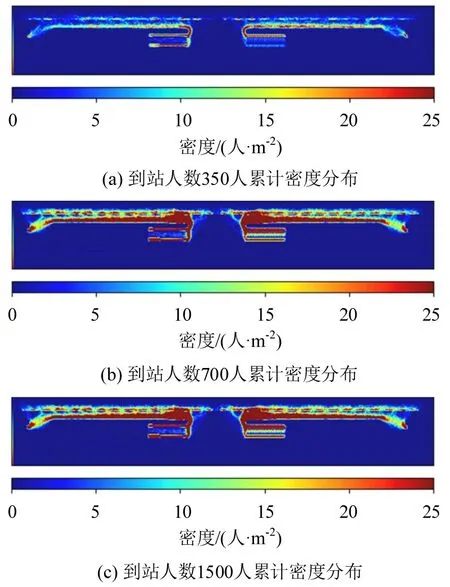
图13 到站客流累计密度分布图Fig.13 Accumulated density distribution chart of arrival passenger flow

通过调整普通行人与步行障碍行人的比例，针对每个比例进行10 次仿真计算，得出平均疏散时间，如表6 所示。可知，随着步行障碍行人比例的增加，站台层乘客的疏散时间呈现逐渐延长的趋势，进而对地铁车站疏散工作产生更为显著的负向影响。

表6 不同行人比例疏散时间表Table 6 Evacuation time schedule for various pedestrian ratios

3.4 无障碍电梯布设方案优化

由图12(c)可以看出，无障碍电梯前存在拥堵现象，现布设方案中无障碍电梯站台层开口朝楼扶梯方向，且位置距终点站方向候车通道较近，当存在较多步行障碍行人时，易导致无障碍电梯区域队列侵入候车通道时间长、面积大等问题。因此，对站台无障碍电梯布设进行优化，如图14 所示。考虑到迪士尼地铁站进出站客流的潮汐特性，将无障碍电梯门朝向改为南北方向，电梯门开口方向可根据站台客流特性动态调整，在早(晚)高峰期间电梯门朝始发(终到)方向开口；在无障碍电梯区域引导步行障碍行人呈U队列。

图14 站台无障碍电梯布设优化图Fig.14 Optimization diagram for placement of platform accessible elevators

基于上述优化方案，仿真参数设置与3.2 节一致，通过重复进行10 次仿真实验获取优化后仿真行人出站用时，得出站台行人至站厅层的平均出站时间约为226 s，相较于优化前行人平均出站时间缩短了约9 s，整体疏散时间提升约为3.8%；优化前后无障碍电梯行人队列侵入情况如表7所示，无障碍电梯侵入站台通道的平均时间占比由22.85%降低至10.57%，提升约为53.74%；优化后站台无障碍电梯区域行人密度时间分布如图15 所示，无障碍电梯梯门朝向的优化减少了行人队列侵入冲突，行人密度优化效果良好。

表7 优化后无障碍电梯行人队列侵入情况统计Table 7 Statistics of queue intrusion in accessible elevator pedestrian flow after optimization

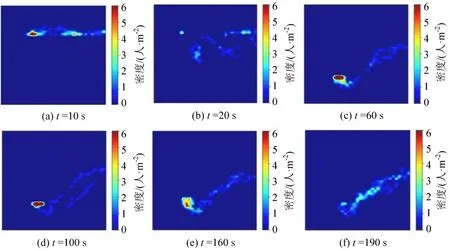
图15 优化后无障碍电梯区域密度时间分布图Fig.15 Temporal distribution chart of area density optimization for accessible elevators

4 结论

本文面向步行障碍人群，考虑其微观出行特性，提出改进元胞自动机模型对步行障碍行人的冲突避让行为进行研究；通过行人场地实验对行人轨迹数据展开分析，对比分析仿真数据与实验数据验证改进模型的有效性。具体结论如下：

(1)分别对轮椅行人、婴儿车行人及携带重物行人进行传统元胞自动机模型行人场域扩展，用以模拟步行障碍行人及其辅助物的共同出行形态，对场强模型进行改进，引入行人辅助物的更新规则，对模型更新规则进行改进。

(2)轮椅行人与婴儿车行人的偏移角度与横向偏移距离相似，在冲突过程中偏移角度和偏移距离均明显小于普通行人；轮椅人员的瞬时速度小于其前方的普通行人，普通行人在感知到前方存在步行障碍行人时，会提前加速避让。

(3)模型仿真得出行人平均速度为1.50 m·s-1，且普通行人、轮椅行人、婴儿车行人仿真得出平均横向偏移距离分别为0.185，0.139，0.155 m，相较于实验行人数据的相对误差分别为2.74%、3.35%、6.71%、6.16%，因此认定本文所建立的考虑步行障碍行人的元胞自动机模型是可行有效的。

(4)对上海地铁11号线迪士尼站进行实际调查与数据采集，基于改进元胞自动机模型，根据调查结果与场地实验数据构建站台仿真场景，对乘客出站场景进行仿真，提出无障碍电梯优化布设方案，对比优化前后布设方案的评价指标，结果表明，优化方案能有效改善站台行人队列侵入情况，提高步行障碍行人通行效率。