A Novel Method for Linear Systems of Fractional Ordinary Differential Equations with Applications to Time-Fractional PDEs

Sergiy Reutskiy,Yuhui Zhang,Jun Luand Ciren Pubu

1A.Pidhornyi Institute of Mechanical Engineering Problems of NAS of Ukraine,Kharkiv,61046,Ukraine

2College of Mechanics and Materials,Hohai University,Nanjing,211100,China

3Nanjing Hydraulic Research Institute,Nanjing,210029,China

4Shigatse Everest Urban Investment and Development Group Co,Ltd.,857000,China

ABSTRACT This paper presents an efficient numerical technique for solving multi-term linear systems of fractional ordinary differential equations(FODEs)which have been widely used in modeling various phenomena in engineering and science.An approximate solution of the system is sought in the form of the finite series over the Müntz polynomials.By using the collocation procedure in the time interval,one gets the linear algebraic system for the coefficient of the expansion which can be easily solved numerically by a standard procedure.This technique also serves as the basis for solving the time-fractional partial differential equations(PDEs).The modified radial basis functions are used for spatial approximation of the solution.The collocation in the solution domain transforms the equation into a system of fractional ordinary differential equations similar to the one mentioned above.Several examples have verified the performance of the proposed novel technique with high accuracy and efficiency.

KEYWORDS System of FODEs;numerical solution;Müntz polynomial basis;time fractional PDE;BSM collocation method.

1 Introduction

A novel numerical method for solving a linear system of fractional ordinary differential equations(FODEs).

is proposed in this paper.Here:n- 1< α≤n; 0 ≤αk < α; positive integerndefines the maximal order of the time derivative in the equation and so, defines the number of the initial conditions of the problem;ϒ(t)= [ϒ1(t),ϒ2(t),....,ϒN(t)]Tis theN-vector of unknowns; ︿Ais a constant non-singularN×Nmatrix and ︿Ak(t), ︿B(t)are time-dependentN×Nmatrices;F(t)= [f1(t),f2(t),....,fN(t)]T.The operatordenotes the Caputo fractional derivative defined by[1,2]:

wherem∈N= {1,2,....}, andΓ(z)denotes the gamma function.In particular, for the power functions we get:

whereN0={0,1,2,....}.

The equations similar to(1)often arise in the modeling of various physical phenomena such as the models of pollution in systems of lakes[3–5],of processing the Magnetic Resonance Imaging(MRI)data[6],of the spread of infections[7,8],and also in modeling the nuclear magnetic resonance[9,10].Recently such problems have become very relevant due to the widespread use of the fractional-order mathematical model of the COVID-19 disease[11–14].

Besides, as is shown below, based on this technique an effective method for solving multi-term time fractional partial differential equations(TFPDEs)of the type

can be developed.Hereai(t)andb(t)are smooth enough functions and

is a spatial differential operator of the second order defined for 0 ≤x≤1.The functionc(x)has the physical sense of the diffusivity as the transport problem is considered.Let us note that Eq.(4)includes many different known equations as particular cases.For example:

– the time-fractional sub-diffusion equation[15]

– the time-fractional telegraph equation[16–18]

– the multi-term time-fractional diffusion and diffusion-wave equations[19–21]

– the time-fractional modified anomalous sub-diffusion equation[22–26]

It has been shown by many researchers that the fractional equations are more suitable for modeling some real-world applications compared with the equations of the integral order.The reviews of some real-world applications of the fractional equations were provided by Almeida et al.[27] and Sun et al.[28], in physics [29], solid mechanics [30], and fluid mechanics [31].The application of fractional equations can also be noted in the recently published books [32,33] and we refer readers to them and to the references therein.

The exact solutions of the fractional equations are critically important for revealing complex physical phenomena.Some well-known analytical methods have been proposed for this goal: the Laplace transform method [34,35], the Green function method [36], the Fourier transform method[37], the variational iteration method [38], the Adomian decomposition method [39], the method of separating variables[40],etc.

However,because analytical solutions are available only for a narrow class of fractional problems,a great number of numerical techniques have been developed.Currently,the finite difference(FD)and finite element(FE)techniques are still the most useful tools in this field.

A survey of the FD methods for solving FODEs and fractional PDEs was presented by Li et al.in [41].Some non-standard FD techniques were proposed to solve complex fractional systems in [42–44].The fast FD methods for the fractional equations were proposed for solving 2D/3D space-fractional diffusion equations in[45,46].Similar fast FD techniques were proposed for distributed-order space-fractional problems in[47],for parameters identifying problems governed by fractional equations in [48], for time-dependent space-fractional diffusion equations with fractional boundary conditions in[49],for the nonlinear fractional wave equation in[50],for fractional equations with singularity in[51],etc.The FE techniques also are the most commonly used for solving fractional equations.The FE approach was used to solve 1D fractional equations in[52,53]and for 2D fractional equations in[54–56].Many works focus on the error analysis of the FE methods such as[57–59].

Recently meshless methods have become the focused issues of the researchers in science and engineering.The meshless methods can be divided into two groups:the pure collocation techniques[60–63] and the methods based on the integration [64–67].To improve the accuracy of the meshless methods combinations with semi-analytical techniques have been proposed.The Laplace transform method has been coupled with the Adomian decomposition method in[68].The analytical and semianalytical solutions of the time-fractional Cahn–Allen equation have been studied by Khater et al.in[69].A semi-analytical solution for the time-fractional diffusion equation has been developed by Kazem et al.in [70].The homotopy analysis transform method [71] and the fundamental solution method[72]belong to the same group of techniques.Five semi-analytical techniques for solving the fractional nonlinear telegraph equation have been studied in[73].

In this paper,a new semi-analytical meshless technique-the backward substitution method(BSM)[74,75] is proposed to solve multi-term linear systems of FODEs.Based on the method provided a flexible and efficient numerical technique is constructed to solve the TFPDE (4).Applying the collocation approach, the original TFPDE is transformed into the system of FODEs which can be handled by the proposed new technique.The performance of this approach has been thoroughly examined by typical numerical examples.The test results are compared with the exact solutions and with the data obtained by other numerical techniques.

The rest of the paper is organized as follows.The detailed scheme of the BSM for solving the system of FODEs is formulated in Section 2.The scheme for solving the TFPDEs is presented in Section 3.The numerical examples are given in Section 4.Finally, some conclusions are briefly discussed in Section 5.

2 Backward Substitution Method for FODEs

In this section,we propose a novel numerical scheme for solving the system(1)subjected to the initial conditions(ICs):

Let us define a new vector-functionP(t)which satisfies the relation

is a known vector function of time.Substituting the relation(11)into the governing Eq.(1),one gets the equation for the new variableP(t)

where

Let us rewrite the system in the form:

Letϕm(t)be the system of basis functions on[0,T]which are chosen in such a way that the righthand side of Eq.(16)can be represented in the form of the series

whereqm=[qm,1,....,qm,N]TareN-vectors to be determined.

Throughout the paper, we use the generalized power functions or the Müntz polynomials basis(MPB)[76,77].A fractional derivative of a Müntz polynomial is again a Müntz polynomial.This is a crucial feature of this base for using it in the collocation methods for Fractional Differential Equations(FDEs).So,we take

as the basis functions and the solution is sought in the class of functions which can be approximated by the MPB and for which there exist fractional derivatives of the original Eq.(1).

Hereσis the parameter of the MPB.The BSM which uses the Müntz polynomials has been developed for solving single FODE in[78–80].The results show that the Müntz polynomials provide quite an accurate approximation of the solution in the range of 0.10 ≤σ≤0.3.Throughout the paper,we useσfrom this interval.

Under the condition(17)the system(16)can be written in the form:

Suppose that the matrix︿Ais invertible.So,we obtain the reduced matrix equation

As it follows from Eq.(3)the analytical expression

satisfies the FODE

Becausen-1<α≤nthe functionΦm(t)satisfies zero ICs

Therefore,the linear combination

is the semi-analytical solution of Eq.(20)for anyqm.It satisfies zero ICs Eq.(15).Let us emphasize:in general case,Eqs.(13)and(20)are different ones.However,if the relation(17)is fulfilled,they are identical.In this caseP∞(t)is also the solution of(13)for any sequenceqm.So,to get the vectorsqmwe substituteP∞(t)into the relation(17)and get the infinite system:

If the Eq.(26)is fulfilled at any time momentt∈[0,T],then the vector functionP∞(t)given in(24)is the exact solution of the problem(13),(15)if it exists.Then the sum(11)is the exact solution of the original problem(1),(10).

In practical calculations,we consider the truncated series

as an approximate solution of the problem(13),(15).It satisfies the truncated analog of the system(20):

and the unknown vectorsqmare obtained by applying the collocation procedure to the truncated analog of(26):

whereNcis the number of the collocation nodestj∈[0,T].We use the Gauss-Chebyshev collocation points:

The collocation system(29)can be written in the compact form:

where

HereMis the number of the Müntz polynomialsϕm(t)andNcis the number of the collocation points in the time interval[0,T].

are also theN×Nsquare matrices.Let us note that to obtain a stable solution of the collocation system the number of the collocation pointsNcis taken twice as large as the number of the Müntz polynomialsM:Nc=2M.Finally,we get the over-determined linear system(31)with the collocation matrixwhich contains 2M2squareN×NblocksCj,m j= 1,....,2M,m= 1,....,M.The matrixhas 2NMrows andNMcolumns.The collocation system is solved by the standard least squares procedure.

So,the algorithm of the solution of the system(31)is as follows:

Step 1.Choose the parameter of the Müntz polynomials basis,σ.

Step 2.Choose the number of the Müntz polynomialsMin the approximate solution.

Step 3.Define the functionsϕm(t)andΦm(t),m=1,...,M(see(21)).

Step 4.Calculate the collocation matrixusing(34)and(35).

Step 5.Calculate the vector of the right hand sideFusing(29),(33).

Step 6.Solve the collocation system(31)forQand find the vectorsqm,m=1,...,Mwhich formQ(see(32)).

Step 7.Getting the functionsΦm(t)m= 1,...,Mand the vectorsqm,m= 1,...,Mobtain the approximate solutionPM(t)(see(27)).

Step 8.Obtain the approximate solution of the original problem (1), (10) as the sumϒM(t)=PM(t)+Θn-1(t)(see(11)).

3 Numerical Scheme for TFPDEs

Let us consider the TFPDE of the form:

subjected to the Dirichlet boundary conditions(BCs)

whereL(x)is a spatial differential operator given in(5).The ICs are determined as follows:

Let us define the new function

where

This function satisfies the equation

under the BCs

and zero ICs

Here

Note:The last terms in(44)can be expressed in the analytical form.Indeed,

where the derivative[tj] can be written using (3).The previous term in (44) can be written as follows:

So,(44)is the analytical expression.

Let us define the functionug(x,t)

which satisfies the BCs(41),(42)and introduce the new variablew(x,t):

The functionw(x,t)is the solution of the TFPDE

where

It is easily to prove that the functionw(x,t)satisfies zero ICs and BCs:

Let us choose a set of linearly independent functionsψi(x),i= 1,...,Ndefined in [0,1].For this goal we mainly use the Multiquadric radial basis function(MQ-RBF)throughout the paper.The centersζjof the RBF are distributed in the solution region[0,1]:

wherecis the shape parameter.We place the centers of the RBFs at the Gauss-Chebyshev points

Based on the numerical experiments carried out we fix the shape parameterc= 0.5 in all the calculations.

We define the modified basis functions

where the coefficientsbj,0,bj,1are chosen to satisfy BCs:

As a result we get the linear system

for each pair of the coefficientsbj,0,bj,1.The system can be solved easily in the analytical form.So,the modified basis functionsφj(x)and their linear combinations satisfy zero boundary condition(56).

We seek the solution of the Eq.(49), in the form of the linear series over the modified basis functionsφj(x)

Substituting Eq.(59)into Eq.(49)we get

Letxi∈[0,1],i= 1,...,Nbe the collocation points distributed inside the solution domain.Applying the collocation procedure at these points,we get the system of the FODEs:

We take the centers of the RBFs as the collocation points:xi=ζi.Let us rewrite the system of the FODEs in the vector form:

So,the system(62)takes the same form as the linear system of FODEs(1)and can be solved by the algorithm described in Section 2.It should be noted that taking into account(51),the vectorϒ(t)satisfies zero ICs:

It means thatΘn-1(t)=0(see(11))andϒ(t)=P(t).UsingMthe Müntz polynomials,we get the approximate solution in the form:

wherePM,j(t)isjthcomponent of the vectorPM(t)given in(27).Then,the approximate solution of the original problem(36)–(38)can be written in the form

3.1 Nonlinear Problem

Let us consider TFPDE(4)with a nonlinear term

Letv0(x,t)be a function considered as the initial approximate solution.Linearization of the functionG(v)in the vicinity ofv0(x,t)

transforms (68) into a sequence of linear TFPDEs each of those can be solved by the technique described above.As a result,we get the iteration procedure.The iterations are stopped with the control of the error|v(x,t)-v(x,t)|or after achieving the prescribed number of iterations.

4 Numerical Examples

In this section several numerical examples are provided to show the accuracy of the proposed scheme.To demonstrate the performance of this technique we consider the different types of errors for systems of FODEs and TFPDEs.

The errors (69), (70) are used in solving systems of the FODEs to estimate the approximate solution of each component of the vectorϒ(t)=[ϒ1(t),ϒ2(t),...,ϒN(t)]T(see Eq.(1)).

The errors(71),(72)are used in solving TFPDE(36)with the BCs(37)and the ICs(38).The errorERMS(t,Nt)also includes the error in the approximation of the first derivative of the solution.The subscriptexofvindicates the comparison with the analytical solution or with the data taken from the literature.The subscriptN,Mofvdefines the numerical solution.For(1+1)dimensional problemsNt= 4N.The numerical experiments show that this relation guarantees the accuracy in the calculation of the errors.To carry out convergence research,we define the convergence order(CO).

4.1 Numerical Experiments for Systems of FODEs

Example 4.1Let us consider the system given in[35]

with the general exact solution

whereEα(t)is the one parameter Mittag-Leffler function

andc1andc2are free parameters which define the ICs.We solve this problem by the suggested scheme forα= 0.25,0.5 and 0.75.The obtained results are reported in Table 1.We use the parameter of the MPBσ= 0.3 andNt= 50000 test points distributed randomly inside [0,1] to calculate the errors(69),(70).

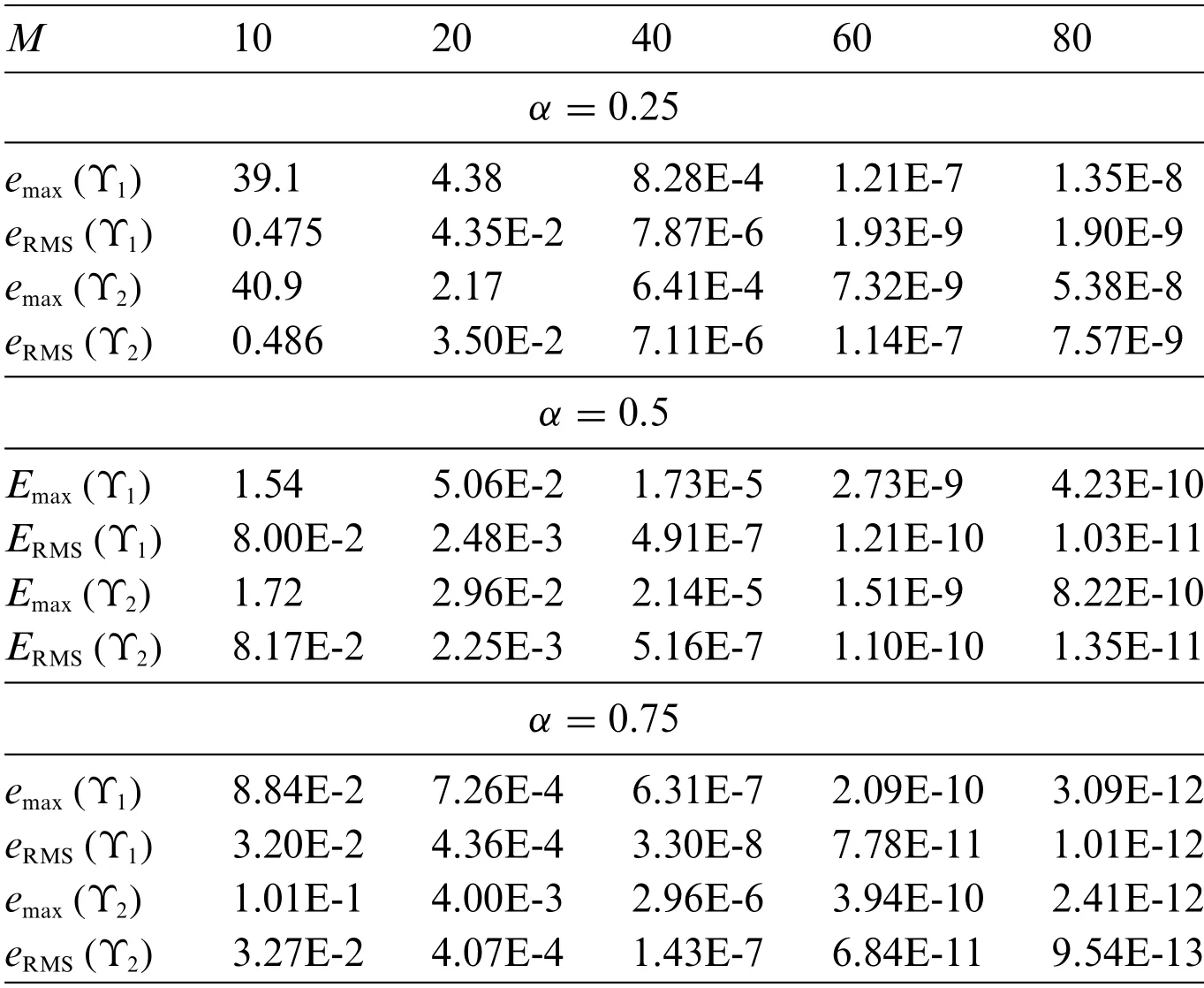
Table 1: The behaviour of the errors with increasing of M for different α

Example 4.2Let us consider the system described in[35]

with the general exact solution

where∂tEα(t)is the first derivative of the one parameter of the Mittag-Leffler function

andc1,c2,c3are free parameters which define the ICs.We solve this problem by the suggested scheme forα=0.5 andc1=c2=c3=1.The obtained results are reported in Table 2.

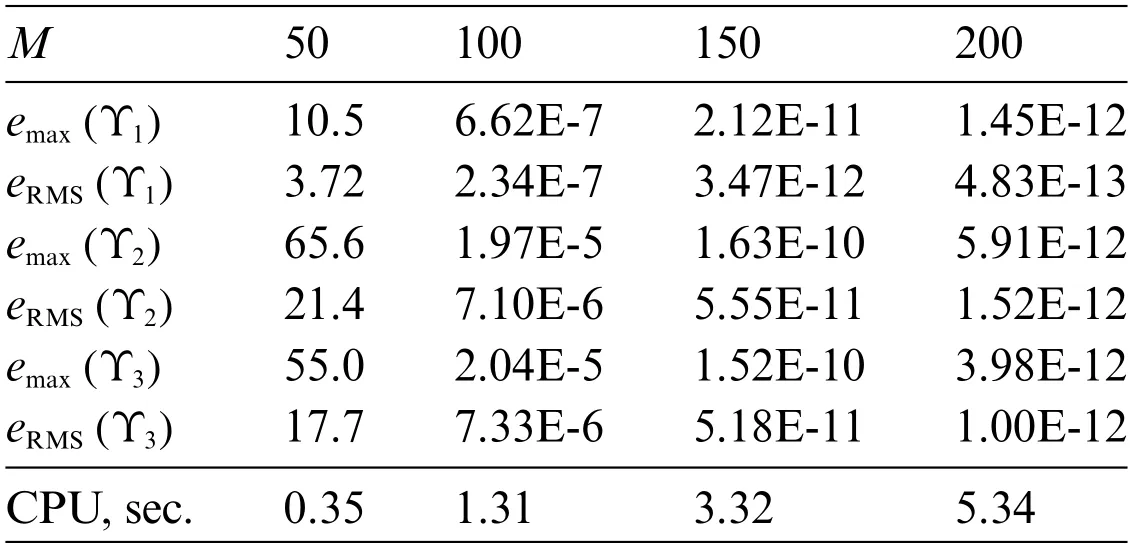
Table 2: The behavior of the errors with the increasing of M

Example 4.3Consider the following initial value problem for the inhomogeneous Bagley–Torvik equation[81]

with the exact solutionV(t)=t+1.As it is shown in[82]the original Bagley–Torvik equation can be rewritten as the system of FODEs of order 1/2

with the initial condition

where the solution of the original Bagley–Torvik equationV(t)=ϒ1(t).It can be easily proved that the exact solution of the system(80)is

According to the method described above,the approximate solution can be written in the form:

where

As it follows from(82),(83)

Thus, the approximate solution (83) contains the exact solutionϒex(t), if the sequenceΦm(t),m=1,...,Mcontains the functionst1/2andt.As it follows from(84),this condition is fulfilled when the sequenceδm+1/2=σ(m-1)+1/2,m=1,....,Mcontains the values 1/2 and 1.For example,ifσ=1/2,thenδm+1/2=1/2,1,3/2,....and the expression(83)contains the exact solutionϒex(t)beginning fromM=2.Forσ=1/4,we get the sequenceδm+1/2=1/2,3/4,1,...and forσ=0.1,we get the sequenceδm+1/2 = 1/2,1/2+0.1,1/2+0.2,1/2+0.3,1/2+0.4,1/2+0.5 = 1,....Thus,forσ=1/4 the exact solutionϒex(t)is included in(83)beginning fromM=3 and forσ=0.1 beginning fromM=6.

The data placed in Table 3 demonstrate that if the approximate solution(83)contains the exact solutionϒex(t),then the method calculates it up to the machine precision.

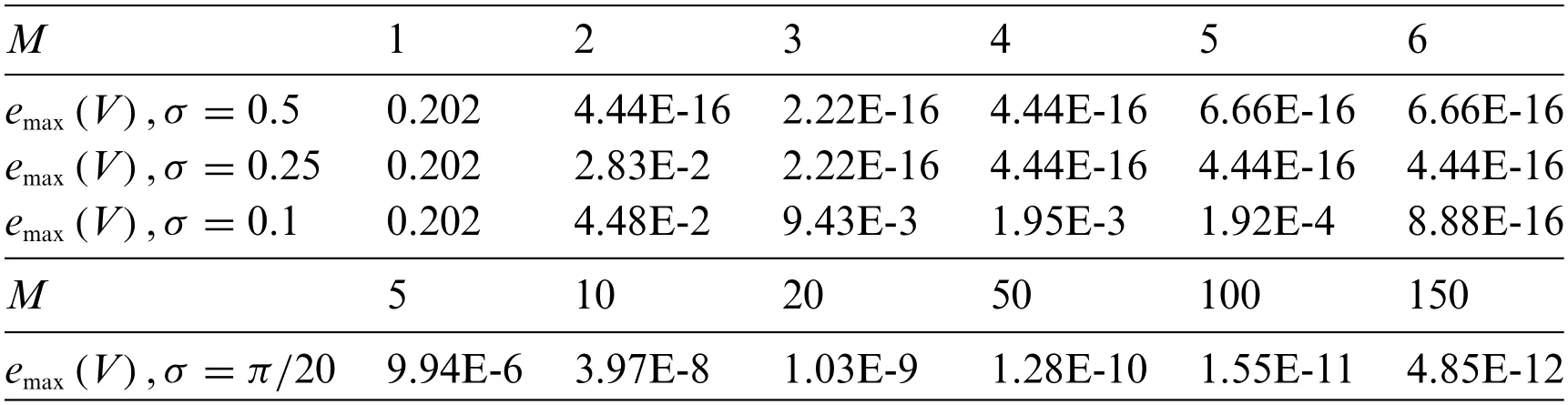
Table 3: The behavior of the errors with the growth of M for different parameter σ

The data placed in the last rows of Table 3 correspond to the general case when the information of the solution is absent.We takeσ=π/20 and there are no sequencesΦm(t),m= 1,...,Mwhich contain the functionst1/2andt.As a result,the error decreases slowly and gradually.The method also provides a high accuracy but with larger values ofM.

The same problem has been studied in[81]on the time intervalt∈[0,5]using fractional linear multistep methods based on the Adams-type predictor-corrector technique.As demonstrated in the paper,the errors depend on time step sizeΔt.For time stepΔt=0.5emax(ϒ1)=-0.15131473519232,and forΔt= 0.0625emax(ϒ1)= -0.00562770408881.These data also are placed in Table C.3 of[2].Note that the componentϒ1(t)corresponds to the solution of the original Bagley–Torvik equation(79).

Table 4 shows the results of the calculation by the proposed method on the time intervalt∈[0,5]with the parameter of the MPBσ=π/20.It is obvious that the method presented provides a much more accurate solution.With a special choice of parameterσthe accuracy is even higher.For example,ifσ=0.25,M=3,thenemax(ϒ1)=4.44E-15 andeRMS(ϒ1)=1.91E-15.

Table 4:The behavior of the errors of the solution on the time interval[0,5]with the growth of M for σ =π/20

Example 4.4Let us consider the multi-term system with time-dependent matrices

The ICs are

The vectorF(t)corresponds to the exact solution

The data placed in Table 5 demonstrate the behavior of the error of the approximate solution with the growth ofMforσ=0.1,0.2 and 0.3.The method converges quite fast for allσ.

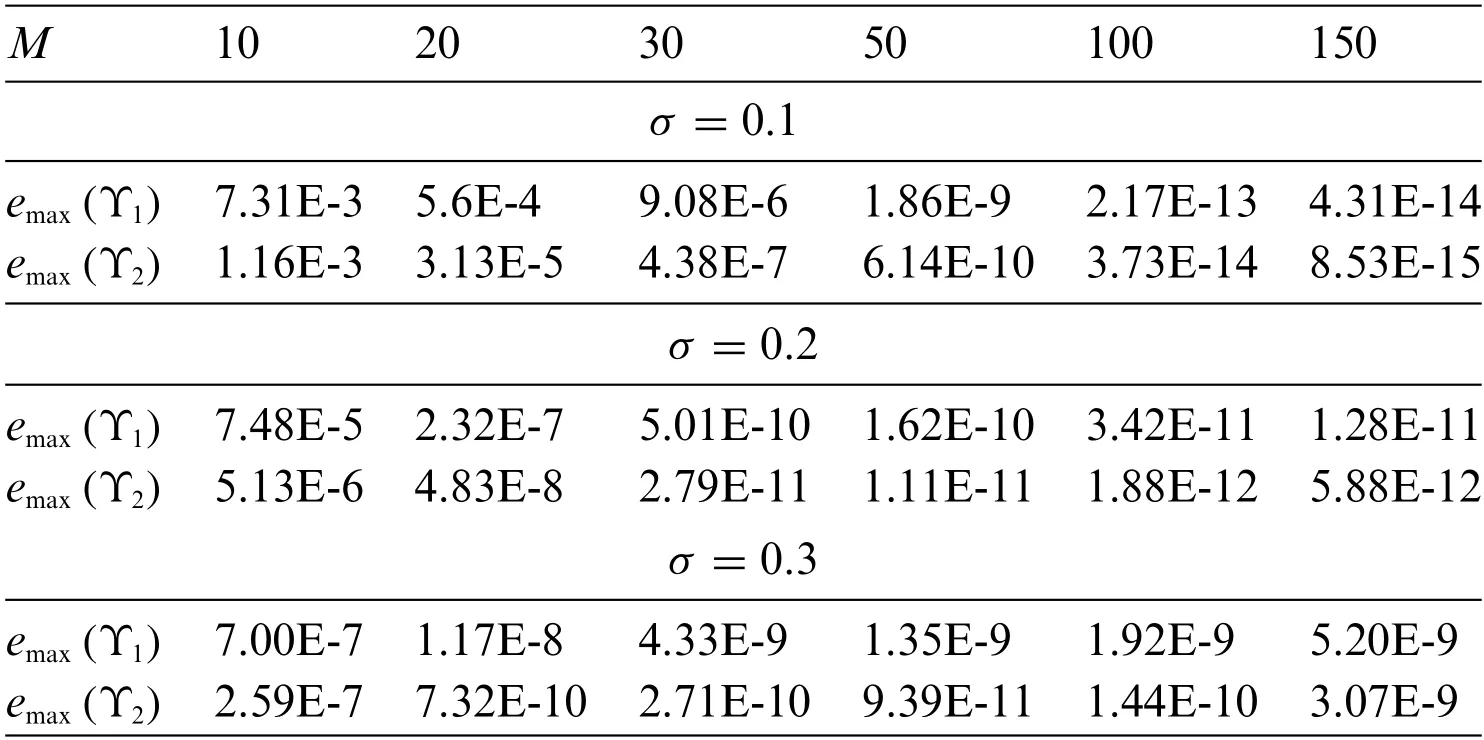
Table 5: The behavior of the errors with the growth of M for different σ

Similar to(83),(84),the approximate solution can be written in the form:

where

In this case we use the additional information that the components of the solutionϒ1(t),ϒ2(t)are analytical functions and can be approximated by the polynomials 1,t,t2,...,tM+1.If we setδm=m+ 1 -, thenΦm(t)∼tm+1and so, the exact solutionϒex(t)belongs to linear span of the polynomials 1,t,t2,...,tM+1.

Table 6 demonstrates a dramatic decrease in the errors with the growth ofMfor this special choice ofδmwhen an additional information on the solution is added.

Table 6:The behavior of the proposed numerical scheme with the growth of M for δm =m+1-

Table 6:The behavior of the proposed numerical scheme with the growth of M for δm =m+1-

4.2 Numerical Experiments for TFPDEs

Example 4.5Let us consider the multi-term TFPDE[83]

Here the source termf (x,t),IC and BCs conform to the exact solutionv(x,t)=1+t2x2-x.

Fig.1 and Table 7 show the behavior of the errors of the approximate solution as the functions ofN(see(59))with the fixedM.ForM= 10 the errors decrease with the growth ofNin the whole range 2 ≤N≤26.This means that the error of the spatial approximation is the dominant error.While forM= 5 the accuracy does not improve forN >10.Therefore,in this case,the dominant error is the error in the solution of the system of FODEs in time.Fig.1 shows that all the curvesEmax(N),ERMS(N)originally lay on the same curve.They move away from this curve depending on the value ofMwhen the error due to approximation in time becomes dominant.

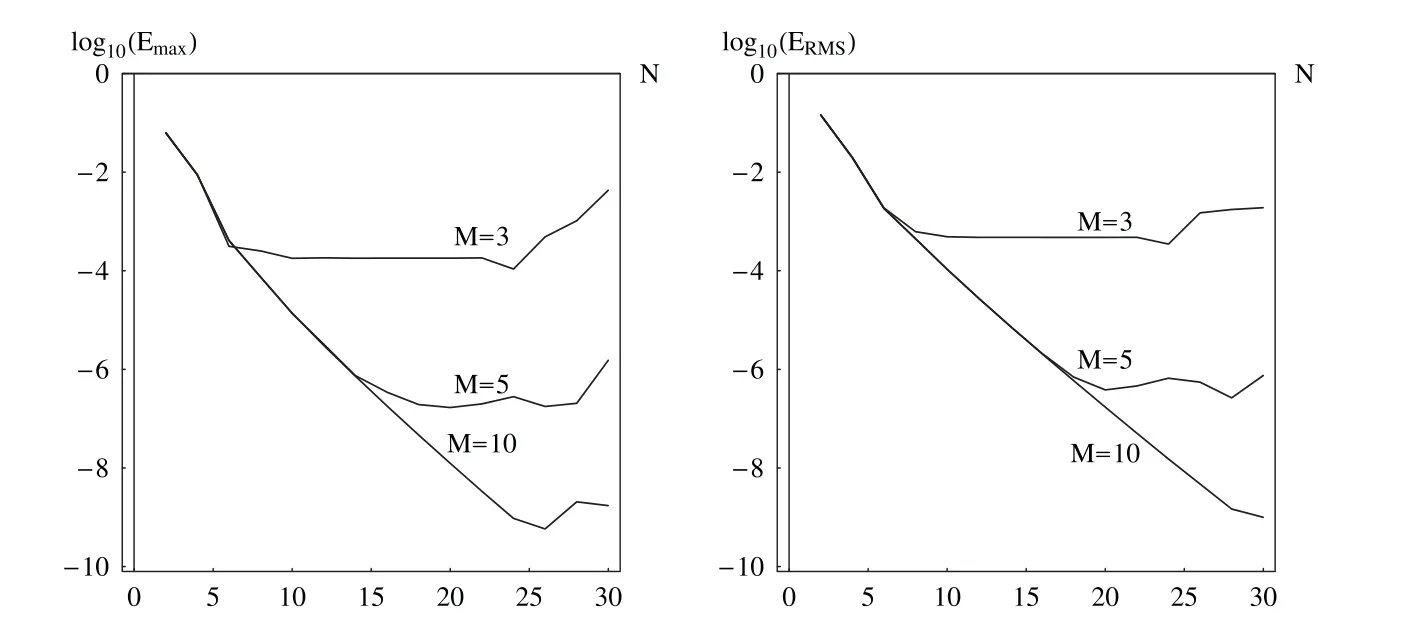
Figure 1:The maximal absolute Emax(left)and ERMS(right)errors as functions of the number of RBFs used in the approximate solution.α =0.95,σ =0.3

Table 7: The Emax,ERMS,and CO vs.N at t=1 with M =10,σ =0.3

Fig.2 and Table 8 show the behavior of the errors as functions ofMwith the fixedN.It is evident that the proposed scheme converges fast with the increase ofM.For the largerMmore accurate results can be obtained.The same problem was studied by Jin et al.in[83]using the Galerkin FE method and FD discretization of the time-fractional derivatives.Usingh= 2-10mesh size and the time step sizeτ= 1/160,they obtained the data placed in the last row of Table 7.The comparison shows that the method presented provides a much more accurate solution.

Table 8: The TFPDE (91) with α = 0.95.The Emax, ERMS, and CO vs.M at t = 1 with N = 26 and σ =0.3

Example 4.6Let us consider the multi-term TFPDE

with the spatial operatorL(x)[v(x,t)] =∂x(cos(x)∂xv(x,t)).The Dirichlet BCs and IC conform to the exact solutionv(x,t)=sin(x+t).

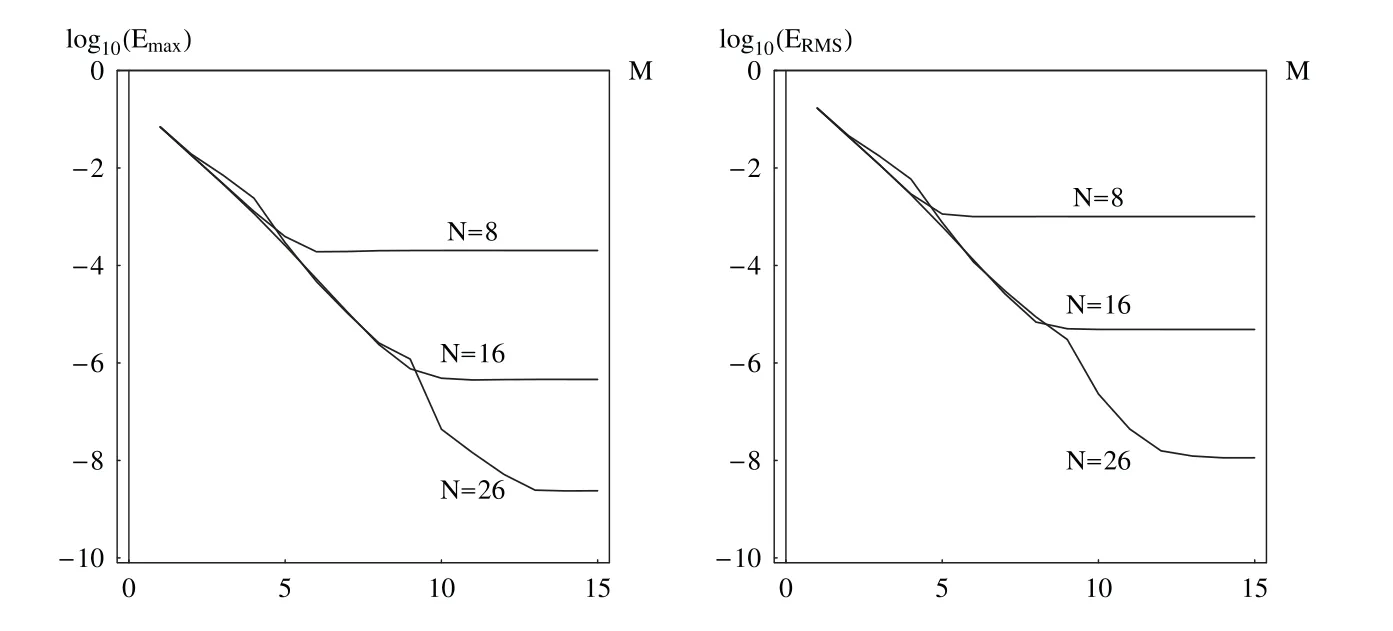
Figure 2:The maximal absolute Emax(left)and ERMS(right)errors vs.M with fixed N.α =0.95,σ =0.3

Table 9 shows the errors,convergence order,and CPU time as the functions ofNwith the fixedM.The data also are illustrated by the graphics in Fig.3.With increasing ofNthe proposed method converges fast, and we can obtain the errors around 10-9withM= 10 andN= 20.It should also be noted that with a small number ofN= 4,the computed errors are around 10-3,which should be sufficient for engineering applications.

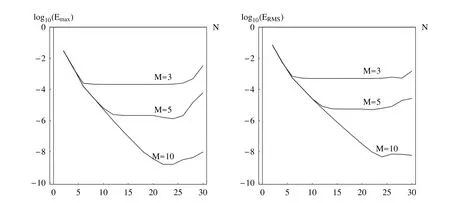
Figure 3:The maximal absolute Emax(left)and ERMS(right)errors vs.N for different M

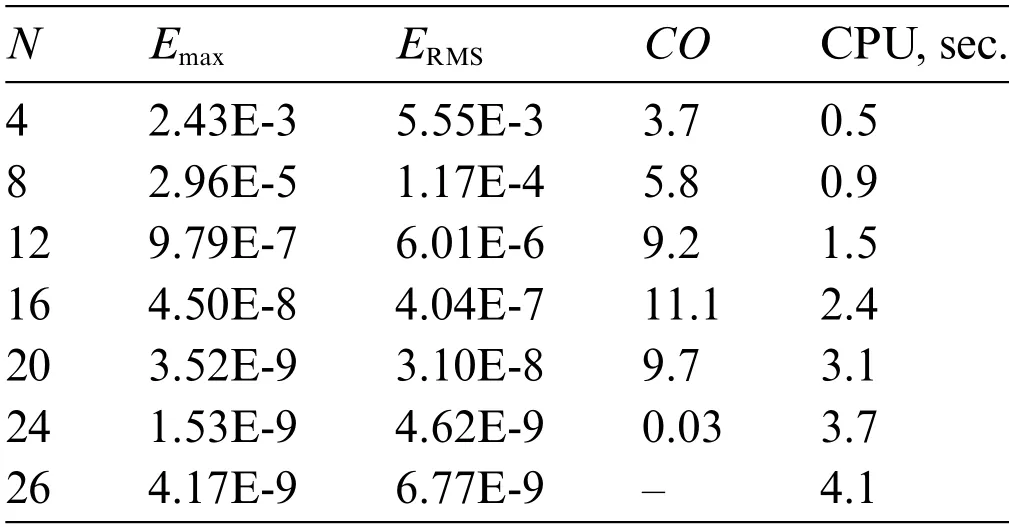
Table 9: The Emax,ERMS,and CO vs.N at t=1 with M =10

Table 10 and Fig.4 show the errorsvs.Mwith the fixedNto verify the performance of the proposed scheme.The order of convergence is larger than 3.

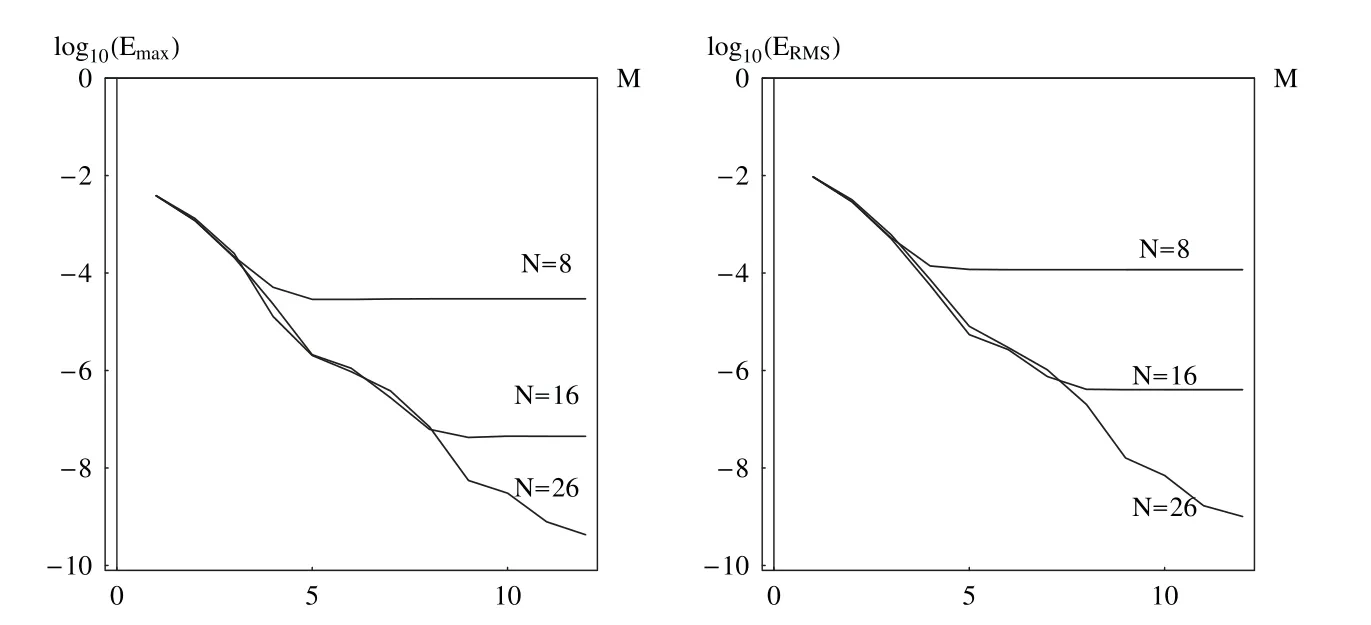
Figure 4:The maximal absolute Emax(left)and ERMS(right)errors vs.M for different fixed N

Table 10: The Emax,ERMS,and CO vs.the M at t=1 with N =26,σ =0.3

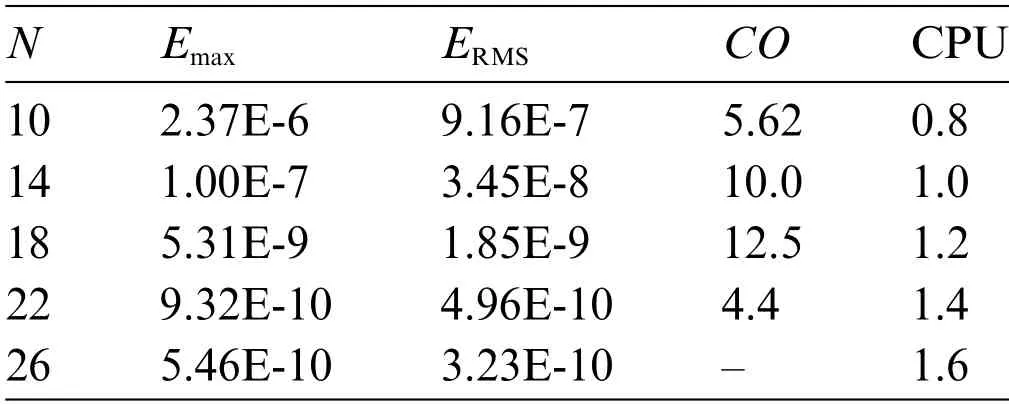
Table 11: The Emax,ERMS,and CO vs.the N at t=1 with M =10,σ =0.3

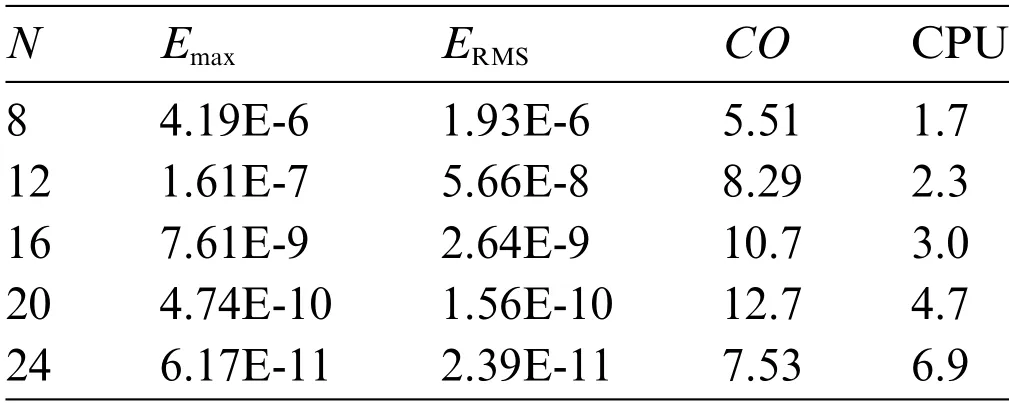
Table 12: The Emax,ERMS,and CO vs.the N at the time moment t=1 with M =25

Example 4.7In the following examples we consider three cases forα >1 to verify the performance of the proposed scheme.

Case 1:Consider the following equation:

Here we have 1<α <2 and the equation needs two ICs

The boundary conditions arev(0,t)=cos(t),v(1,t)=cos(t+1).

The exact solution of the problem isv(x,t)=cos(x+t).

Case 2:Consider the following equation:

with the spatial operatorL(x)[u(x,t)] =∂x(cosh(x)∂xu(x,t)).Here we have 2< α <3 and the equation needs three ICs

The boundary conditions arev(0,t)=sin(t),v(1,t)=sin(t+1).

The exact solution of the problem isv(x,t)=sin(x+t).

Case 3:Consider the following equation:

with the spatial operatorL(x)[v(x,t)] =∂x(sinh(x)∂xv(x,t)).Here we have 3< α <4 and the equation needs four ICs

The boundary conditions are

The exact solution of the problem isv(x,t)=sin(x+t).

Tables 11, 12 show the errors with increasing ofNwith the fixedM.It is evident that the proposed scheme provides very accurate results.Furthermore,for a small number ofN,we can also get moderately accurate results with errors around 10-6.For largerNthe proposed scheme converges faster.The accuracy of the proposed method is also demonstrated in Fig.5.Finally,Table 13 shows the error when the Gaussian RBF expis used in spatial aproximation.For a small number ofNthe Gaussian RBF provides a more accurate solution than the MQ-RBF.For largeNboth RBFs provide the results with errors of the same level of accuracy.

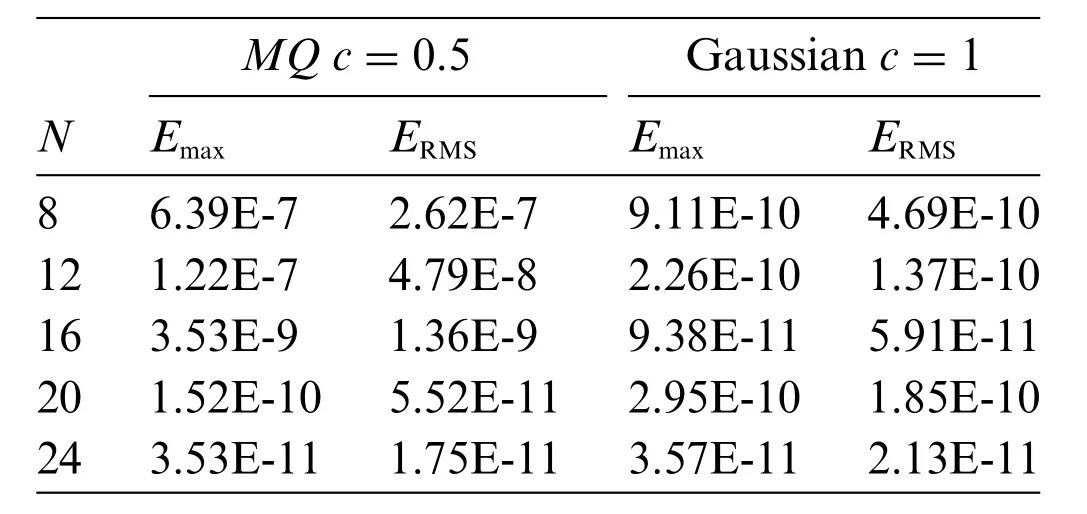
Table 13:The errors vs.N at t=1 with M =25 using the MQ and the Gaussian as the basis functions

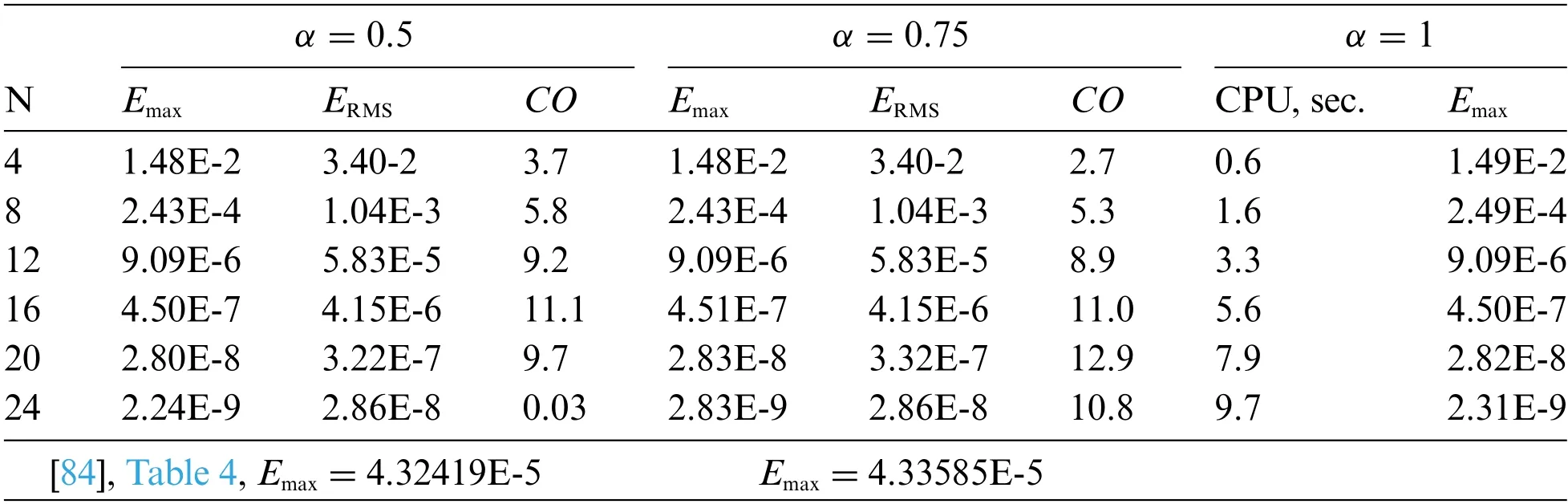
Table 14:The errors concerning the change of the number of modified RBF N at time moment t=1 with γ =0.1,M =12

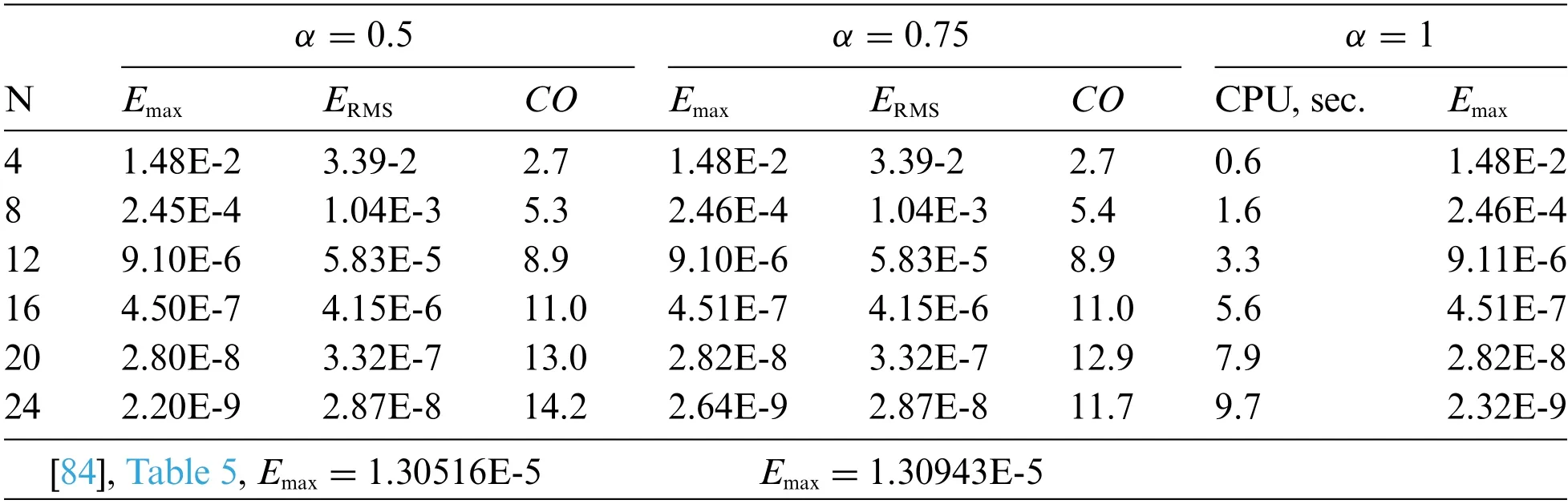
Table 15:The errors concerning the change of the number of modified RBF N at time moment t=1 with γ =0.5,M =12

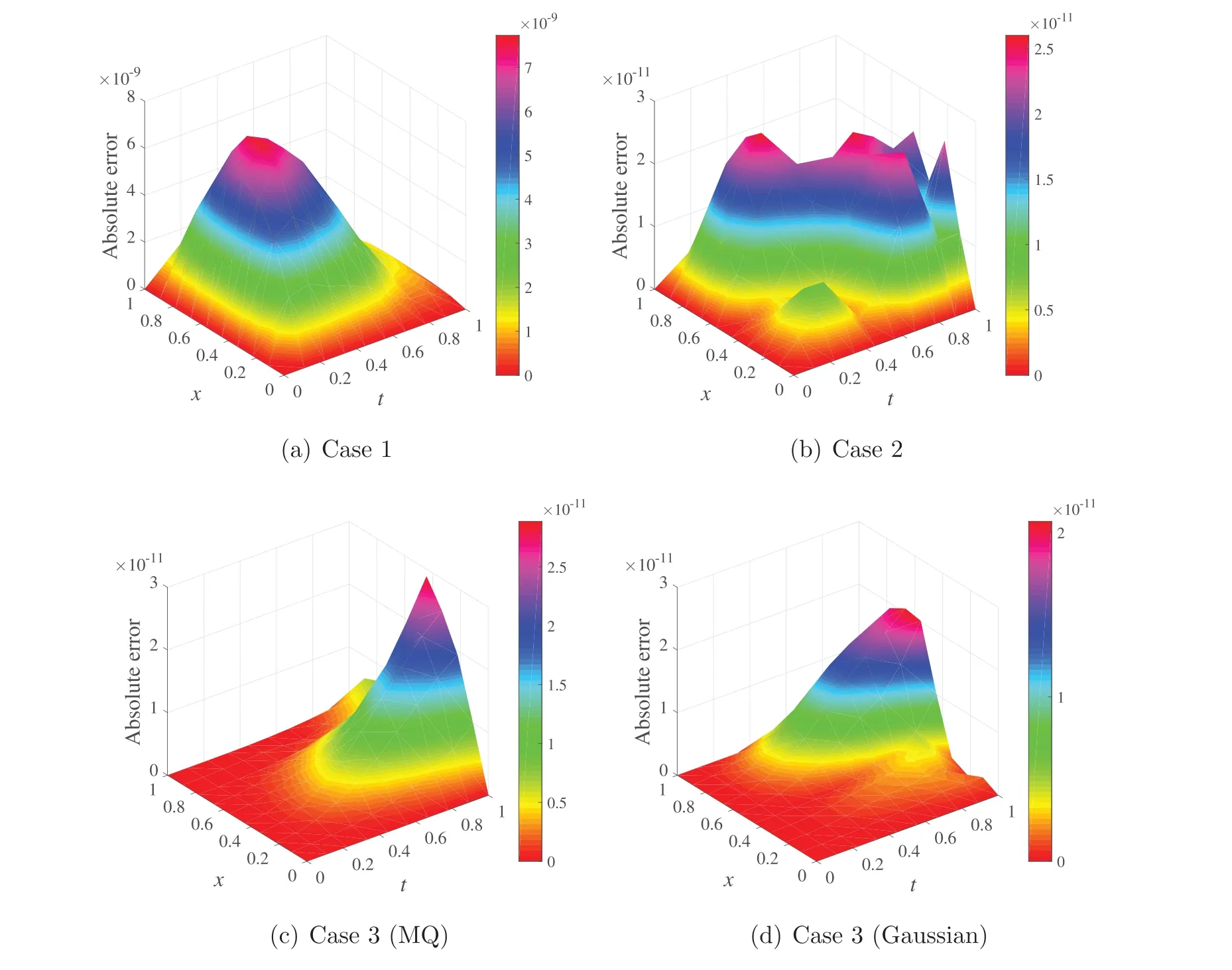
Figure 5:The domain absolute errors

Example 4.8Consider the nonlinear time-fractional the Huxley-Burgers’equation of the following form:

The Dirichlet BCs and IC conform to the exact solutionv(x,t)=x3(t+1).

Tables 14, 15 and Fig.6 show the behaviour of the errors with the growth ofNand the fixedM.The data are obtained after 3 iterations of the quazilinearization procedure.The same problem was considered by Hadhoud et al.in [84] using a numerical technique based on the cubic B-spline collocation method and the mean value theorem for integrals.The maximal absolute errors obtained there for the mesh sizeΔx= 0.01 and the time stepΔt= 0.01 are shown in the last rows of the tables.The last columns of the tables contain the data corresponding toα=1,i.e.,to the solution of the equation of the integer order.These data demonstrate that the proposed method can be used for solving equations of fractional order as well as equations of integer order without any modification of the algorithm.

Example 4.9Consider the TFPDE

Figure 6: The maximal absolute Emax (left) and ERMS (right) errors as functions of the number of the RBFs N used in the approximate solution.The data correspond to α =0.5,γ =0.1

The source functionf (x,t),Dirichlet BCsv(0,t)=v(1,t)= 0 and ICv(x,0)= 0 conform the exact solutionv(x,t)=x4(1-x)tαwith the strong singularity att=0.

Table 16 shows the behavior of the errors with the growth ofNwith the fixedM= 12 and with the parameter of the MPBσ= 0.3.The same problem was considered by Ferrás et al.in[85]using a numerical technique based on the combination of the method of lines with the hybrid collocation method.The maximal absolute errors obtained there are shown in the last row of the table.

Table 16:The errors concerning the change of the number of modified RBF N at time moment t=1 with M =12

5 Conclusion

This paper presents a new meshless technique for solving multi-term linear systems of fractional equations.These systems have been used in modeling various phenomena in different branches of engineering and science.Using substitution(11),we transform the original system into the one for the vector variableP(t)which satisfies zero ICs.ThenP(t)is sought in the form of the finite series over the Müntz polynomials basis.Applying the collocation procedure in the domain, we get the linear algebraic system solved by the standard numerical procedure.Then, on the base of this technique,the method of solving the TFPDE has been developed.The collocation at the centers of the RBF transforms the TFPDE into a system of FODEs similar to the one considered in Section 2.

In the authors’opinion,the main results achieved in the paper are:(1)The effective method for solving systems of the FODEs with time-dependent coefficients has been developed and tested.(2)On the base of this technique the method of solving TFPDEs of the high fractional order has been proposed.The method has been tested on the problems with the highest derivative of the orders:1< α <2, 2< α <3 and 3< α <4.(3) The technique has been extended to nonlinear the Huxley-Burgers’TFPDE.It should be stressed that the proposed method can be used for solving both equations of fractional and integer order without any modification of the algorithm.

Some remarks:(1)In this paper the MQ-RBF is mainly used for spatial approximation.However,the last example demonstrates that the Gaussian RBF is suitable for this purpose.The other global RBFs, compactly supported RBFs and B-splines also can be used for spatial approximation in the framework of the proposed technique.(2)Only the Dirichlet BCs are considered in this study.However,the proposed technique can be extended to the problems with the boundary conditions of the general type by some modification of the Eqs.(56)–(58).(3) Only (1 + 1) dimensional problems have been considered.However,using multidimensional RBSs,this approach can be extended to the(2+1)and(3+1)dimensional problems.

It should be remarked that the limitation of the presented technique is caused by the fast growth of the size of the collocation matrixof the linear system(31)with the growth ofNandM.Becauseis the dense matrix the problem of ill-conditioning also arises.

To overcome this problem we presuppose the use of a localized scheme of the spatial approximation based on the compactly supported radial basis functions(CSRBF)in the future to avoid dense and ill-conditioning matrices.

To overcome the problems of calculations on the large time interval[0,Tmax],we think of using the approach developed in[86].

Let[0,Tmax]represent a sum of the subintervals:[0,Tmax]=[0,T]∪[T,2T]∪....∪[(L-1)T,LT].

Solving the Eq.(1)in the first subinterval[0,T],we use the ICs(10)of the original problem.As a result of the solution we get the vectors

which can be used as the initial data for solving the equation in the second subinterval [T,2T].

Applying the transform

t=τ+T,

We get the equation for the unknown vectorϒ2(τ)defined on the intervalτ∈[0,T]:

Then,the vectorsϒ2(T),∂tϒ2(T),...,(T)are used as the ICs for solving on the intervalt∈[2T,3T], etc.So, we solve the original equation at the same time intervalτ∈[0,T] with the time-dependent coefficients computed at the shifted timeτ+lT.The calculations are continued tillt=LT=Tmax.We can chooseTsmall enough to reduce the valueMand so the size of the collocation matrix.It is worth emphasizing that in the paper mentioned above the system of 3 FODEs has been solved on the time interval[0,Tmax] = [0,5000].All these items mentioned above will be the subjects of the further study.

Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions whose efforts have helped to improve the quality of this paper.

Funding Statement:This research was funded by the National Key Research and Development Program of China(No.2021YFB2600704),the National Natural Science Foundation of China(No.52171272),and the Significant Science and Technology Project of the Ministry of Water Resources of China(No.SKS-2022112).

Availability of Data and Materials:Sergiy Reutskiy:Methodology and Writing–Original Draft;Yuhui Zhang:Writing–Review&Editing;Jun Lu:Writing–Review&Editing;Ciren Pubu:Validation.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.