An Effective Hybrid Model of ELM and Enhanced GWO for Estimating Compressive Strength of Metakaolin-Contained Cemented Materials

Abidhan Bardhan,Raushan Kumar Singh,Mohammed Alatiyyah and Sulaiman Abdullah Alateyah

1Department of Civil Engineering,National Institute of Technology Patna,Patna,India

2Department of Computer Engineering and Applications,GLA University,Mathura,India

3Department of Computer Science,College of Sciences and Humanities-Aflaj,Prince Sattam Bin Abdulaziz University,Al-Kharj,Saudi Arabia

4Department of Computer Science,College of Science and Arts,Qassim University,Unaizah,Saudi Arabia

ABSTRACT This research proposes a highly effective soft computing paradigm for estimating the compressive strength(CS)of metakaolin-contained cemented materials.The proposed approach is a combination of an enhanced grey wolf optimizer (EGWO) and an extreme learning machine (ELM).EGWO is an augmented form of the classic grey wolf optimizer(GWO).Compared to standard GWO,EGWO has a better hunting mechanism and produces an optimal performance.The EGWO was used to optimize the ELM structure and a hybrid model, ELM-EGWO,was built.To train and validate the proposed ELM-EGWO model, a sum of 361 experimental results featuring five influencing factors was collected.Based on sensitivity analysis,three distinct cases of influencing parameters were considered to investigate the effect of influencing factors on predictive precision.Experimental consequences show that the constructed ELM-EGWO achieved the most accurate precision in both training(RMSE=0.0959)and testing (RMSE = 0.0912) phases.The outcomes of the ELM-EGWO are significantly superior to those of deep neural networks (DNN), k-nearest neighbors (KNN), long short-term memory (LSTM), and other hybrid ELMs constructed with GWO,particle swarm optimization(PSO),harris hawks optimization(HHO),salp swarm algorithm(SSA),marine predators algorithm(MPA),and colony predation algorithm(CPA).The overall results demonstrate that the newly suggested ELM-EGWO has the potential to estimate the CS of metakaolin-contained cemented materials with a high degree of precision and robustness.

KEYWORDS Metakaolin-contained cemented materials;compressive strength;extreme learning machine;grey wolf optimizer swarm intelligence;uncertainty analysis;artificial intelligence

Abbreviations

Adj.R2Adjusted coefficient of determination

ANN Artificial neural network

B/S Binder to sand ratio

BBO Biogeography-based optimization

CO2Carbon dioxide

CPA Colony predation algorithm

CS Compressive strength

CSS Charged system search

DE Differential evolution

DNN Deep neural network

E&E Exploration and exploitation

EGWO Enhanced grey wolf optimizer

ELM Extreme learning machine

ELM-CPA Hybrid model of ELM and CPA

ELM-EGWO Hybrid model of ELM and EGWO

ELM-GWO Hybrid model of ELM and GWO

ELM-HHO Hybrid model of ELM and HHO

ELM-MPA Hybrid model of ELM and MPA

ELM-PSO Hybrid model of ELM and PSO

ELM-SSA Hybrid model of ELM and SSA

EP Evolutionary programming

FOF Field of forces algorithm

GA Genetic algorithm

GGBS Granular glass furnace slag

GP Genetic programming

GSA Gravitational search algorithm

GWO Grey wolf optimizer

HHO Harris hawks optimization

KNN K-nearest neighbors algorithm

lbLower bound

LCA League championship algorithm

LSTM Long short-term memory

M Cement grade

MH Meta-heuristic

MK Metakaolin

MK/B Metakaolin to binder ratio content

ML Machine learning

MLA Machine learning algorithm

MPA Marine predators algorithm

NHNumber of hidden neurons

NSSwarm size

PFI Performance index

PSO Particle swarm optimization

R2Coefficient of determination

RMSE Root mean square error

RSR RMSE to standard deviation of actual observations

SLC Soccer league competition

SLFNN single layer feed-forward neural network

SLO Social learning optimization

SO Spiral optimizer

SOA Seeker optimization algorithm

SPSuperplasticizer

SSA Salp swarm algorithm

SVR-PSO Hybrid model of SVR and PSO

TLBO Teaching-learning-based optimization

tmaxMaximum epoch count

TR Training

TS Testing

ubUpper bound

VAF Variance account factor

W/B Water-binder ratio

WCA Water cycle algorithm

1 Introduction

Concrete is a broadly utilized material in the construction industry.In the field of civil engineering,composite concrete technology is used to make concrete and cement-based materials, which are made up of cement, reinforcement, filler materials, admixtures, and water [1].These materials are extensively used in the construction industry due to their high mobility, early strength gain, strong durability,and many other characteristics.For the construction of important structures such as precast concrete frames[2],reinforced concrete frames[3–5],composites reinforced columns and beams[6,7],steel-concrete composite beams[8],composite structure conducted under severe conditions[9],these materials also play an important role.During the process of cement manufacturing,a large amount of CO2is released into the air which is a great threat to the environment.Practically,5%of the total CO2emission is mainly due to the production of cement[1,10–12].The environmental damage caused by the mining of such large quantities of raw materials,the construction industry faces increasing pressure to cut the amount of cement consumption in concrete or to replace a proportion of cement content with supplemental materials such as recycled aggregates.According to the source of availability,supplementary materials can be classified into the following categories(a)natural materials such as natural pozzolans; (b) industrial wastes, viz., slag, fly ash, silica fume, etc.; and (c) environmentally friendly materials such as granular glass furnace slag(GGBS),metakaolin(MK),etc.[1,10].Notably,the production energy of GGBS and MK is less demanding and thus more environmentally friendly.Among these two,MK is an aluminosilicate substance that is created by calcining kaolin clay at high a temperature.MK is a high-performance mineral additive and has better pozzolanic properties than silica fume[13,14].

Extensive research works on the production and characterization, and effect of MK on the physico-chemical characteristics of cement, mortars, and concrete have been carried out since the mid-20th century [15,16].The partial replacement of cement with MK has shown a substantial effect on both the fresh and hardened properties of MK-cement mixtures, providing an alternative to standard cement-sand mixtures.Due to the pozzolanic reaction between MK and portlandite,the addition of MK to concrete/cement mortar causes the consumption of portlandite formed during the hydration phase of Portland concrete resulting in the generation of extra C-S-H gel and crystalline substances [13,14].The optimal proportion of MK replacement varies among studies and depends on several factors such as the composition of Portland cement,water-binder ratio(W/B),proportion of superplasticizer (SP), and the properties of MK.The pozzolanic reaction and filler effect lead to the refinement of pores in the hardened mix of MK-contained concretes, resulting in a decrease in pore size and increasing total porosity.According to the literature, the compressive strength (CS)of concrete/cement increases with MK content when used as partial cement replacement, but the optimum percentage for maximum long-term strength varies.Concrete mixes with MK also exhibit enhanced durability and workability,better resistivity against chemical attack,reduced permeability and efflorescence,and reduced the effect of alkali-silica reaction.The part replacement of cement with GGBS and/or MK not only improves concrete durability but also reduces the risk of thermal cracking in the produced mix[17–19].

Although MK may increase the susceptibility of concrete to carbonation by consuming portlandite, there are cases where MK enhances carbonation resistance.Overall, replacing cement with MK increases the durability of mortar and concrete.According to earlier research,the part replacement of cement with MK has a good effect on the strength and durability of mortar and concrete;therefore, MK can serve as a carbon-neutral substitute for pure Portland cement concrete/mortar.In the past, numerous experimental works have been conducted to examine the impact of various factors,such as the proportion of cement replaced by MK,the age of the specimen during testing,and the ratio of aggregates to binder, on the CS of concrete and cement containing MK.Furthermore,statistical models have been developed to predict their CS.However,the vast number of variables and complexity of the subject make it difficult to incorporate all parameters into these formulas,rendering them specific to certain materials and not generally applicable.Additionally,researchers have tested the CS of cement in the laboratory, but the laboratory tests can be time-consuming, expensive, and labour-intensive.Therefore,there is a need for a more resourceful and cost-effective method to estimate the CS of concrete and cement-based materials containing MK.

Machine learning(ML)is a multi-disciplinary area of research concerned with the development of intelligent inferences that can learn and draw inferences from patterns in data.Its main goal is to simulate and implement human learning behavior, enabling the acquisition of new skills and the continual improvement of existing skills [20,21].By leveraging the powerful data processing and analysis abilities of computers, ML can effectively process and analyse large quantities of data.In recent times, ML paradigms have been applied in various fields due to their superior performance.Given its outstanding performance, many researchers have proposed multiple ML approaches to estimate the characteristics of cement and concrete, yielding satisfactory outcomes.In the field of CS prediction of concrete and cement, Özcan et al.[22] presented comparative results of prediction outcomes of neural network and fuzzy logic paradigms for the long-term CS of silica fume-based concrete.Sarıdemir [23,24] used ANNs and fuzzy logic for predicting CS of concretes and mortars containing MK and silica fume.Gilan et al.[25]suggested an SVR-PSO paradigm for the prediction of CS of MK-contained concretes.Moradi et al.[26] studied predicting the CS of MK-contained concrete with different properties using ANN.Asteris et al.[1]used ANN to reveal the nature of MKbased concrete.Huang et al.[10] predicted the CS of cement-based materials with MK used on the hybrid ML paradigm.Although the aforementioned ML paradigms achieved satisfactory results in predicting the CS of concrete and cement, they have multiple limitations such as uncertainty, time consumption,and local minima trapping issues.Thus,it is necessary to develop a high-performance ML paradigm,especially for estimating the CS of MK-contained cement-based materials.

According to the literature,to overcome the afore-mentioned limitations and enhance the application of hybrid ML paradigms,this research suggests a high-performance ML solution for predicting the CS of cement containing MK.To this end,enhanced GWO(EGWO),proposed by Joshi et al.[27],was employed to optimize the weights and biases of ELM.EGWO is an augmented form of the classic GWO.Compared to standard GWO,EGWO has a better hunting mechanism and produces an appropriate balance between exploration and exploitation(E&E)that leads to optimal performance.The developed model was then used for the estimation of CS of MK-contained cement-based materials.The outcomes of the ELM-EGWO were also compared with six more hybrid ELMs constructed with GWO, PSO, HHO, SSA, MPA, and CPA and three standalone models including DNN,KNN,and the LSTM.

The subsequent part of this work is ordered as follows:Section 2 offers research significance which is followed by the details of the ELM and an overview of MHs in Section 3.Descriptive information of the datasets and the computation modelling procedure are presented in Section 4.The results and discussions are presented in Section 5,while in Section 6,a summary and conclusions is provided.

2 Research Significance

With non-linear association between the parameters and the concrete qualities,it is challenging to construct optimal concrete mixes incorporating metakaolin[1].For the optimal mix design,expensive and time-consuming experimental operations based on empirical formulas are typically conducted.In addition, the literature and current tools for predicting the CS of concrete and cemented materials reflect this challenge, where empirical correlations are suggested to account for the consequence of a small number of parameters on the concrete CS.Most of the existing models employ diverse parameters and provide findings with a substantial variation, highlighting the need for additional studies.In addition,alternative methods that can produce optimum outcomes with fewer input data are required.

The existing literature across several technical and scientific disciplines provides evidence that soft computing techniques,known for their proficiency in non-linear modelling,can establish correlations between desired outcomes and a range of influencing parameters,whether they have direct or indirect impacts [1,28–32].Considering the effects of influencing parameters, it is possible to design a highperformance soft computing-based paradigm using existing experimental data from numerous sources.As stated previously, the selection of an effective soft computing model is however a difficult task for the following reasons: (a) model implementation without considering the effects of individual variables;(b)inappropriate model construction and validation;(c)inability of employed models to find the exact global optimum;(d)overfitting-related issues,etc.In order to estimate the intended output,such as the CS of concrete,it is necessary to develop a high-performance intelligence paradigm that takes into account the effects of influencing parameters and overfitting related concerns.Considering the afore-mentioned discussion as a reference,this study suggested a highly effective hybrid model,i.e.,ELM-EGWO,for estimating the CS of cemented materials.To this end,a comprehensive record was collected from the work of Huang et al.[10].The outcomes of the suggested ELM-EGWO paradigm were analysed and compared for three different input combinations.For this purpose,three standalone models(viz.,DNN,KNN,and LTSM)and six additional hybrid ELMs constructed with GWO,PSO,HHO,SSA,MPA,and CPA algorithms,were used in the present research.

3 Methodology

This section discusses the working concept of ELM, followed by the classification of MHs.Following that, details of GWO and EGWO are presented.At the end, the methodological details for hybrid ELM development are provided.Notably,detailed information on the utilized MHs is not offered because they are well-established and the works of PSO[33],HHO[34],SSA[35],MPA[36],and CPA[37]can be referred to for more detail.Similarly,the literature on DNN[38,39],KNN[40,41],and LSTM[42,43]can be referred to for information regarding the working principle and application domain of these paradigms.

3.1 Extreme Learning Machine

ELM[44],a widely used soft computing algorithm that is used for both regression and classification tasks.It is also called single layer feed-forward neural network(SLFNN).With the use of an advanced SLFNN, a closed-form solution for the weights of the outputs is produced by the ELM.It has only one hidden layer with one or more hidden neurons (see Fig.1).The input and output layers each include the same number of nodes as their corresponding input and output parameters.In ELM,the weights and biases are assigned at random,which remains constant during the course of operation.Contrary to usual feed-forward networks where iterative procedures are followed,adapting to the ELM is carried out through a continuous-time function of the distribution of probability,which provides lower design complexity and is capable of solving problems faster using random weights and biases for the hidden layers, along with a unique solution in the output by employing the Moore-Penrose pseudo inverse function[44].

Figure 1:Structure of ELM

A set of predictor asxiand the target asyiin a series of d-Dim vectors fori=1,2,...,Nsamples;the SLFNN havingLhidden layers is demonstrated as below:

whereβ=[β1,β2...βL]Trepresent the output weight matrix;h(x)=[h1,h2...hL]is the outputs of the hidden layer;h(x)is theithhidden node.Therefore,the output function,hi(x),can be given as:

whereG(ai,bi,x)is represented by the hidden neuron variables (a,b), is considered as a nonlinear continuous function.The sigmoid function is generally used for developing the ELM model,Huang et al.[44]emphasized that the approximation error should be optimized to solve the weights in the hidden and output layers (β) using minβ∈RL×m‖Hβ-T‖2, where ||Hβ-T|| demonstrates the Frobenius norm andHrepresents the hidden-output matrix as follows:

The target matrix in the training phase can be defined as:

An optimal response is provided throughβ∗=H+T, whereH+represents the Moore-Penrose generalized inverse function(+).The optimal solution is then applied to provide a prediction for given input vectors,x.Successful application of ELMs can be found in the literature[45,46].

3.2 MH Algorithms

As of date, several MHs have been introduced.Based on their source of inspiration, MHs can be classified into various groups including(a)evolutionary algorithms(EAs),(b)swarm intelligence(SI)algorithms,(c)natural phenomena-based algorithms,and(d)human inspiration algorithms[47].The inspiration for EAs is dependent on the simulation of natural genetic concepts, e.g., mutation,selection,and crossover.BBO[48],DE[49],EP[50],GA[51],and GP[52]belong to this group.The SI techniques simulate the behavior of a swarm in nature in the course of searching for food.The MHs under this category are CPA[37],GWO[53],HHO[34],MPA[36],PSO[33],SSA[35],and so on.The natural phenomena-based techniques include CSS[54],FOF[55],GSA[56],SO[57],WCA[58],and so on.The human-inspired algorithms are dependent on inspiration from human behavior.Examples are LCA[59],SLC[60],SLO[61],SOA[62],TLBO[63],etc.These groups are illustrated in Fig.2.

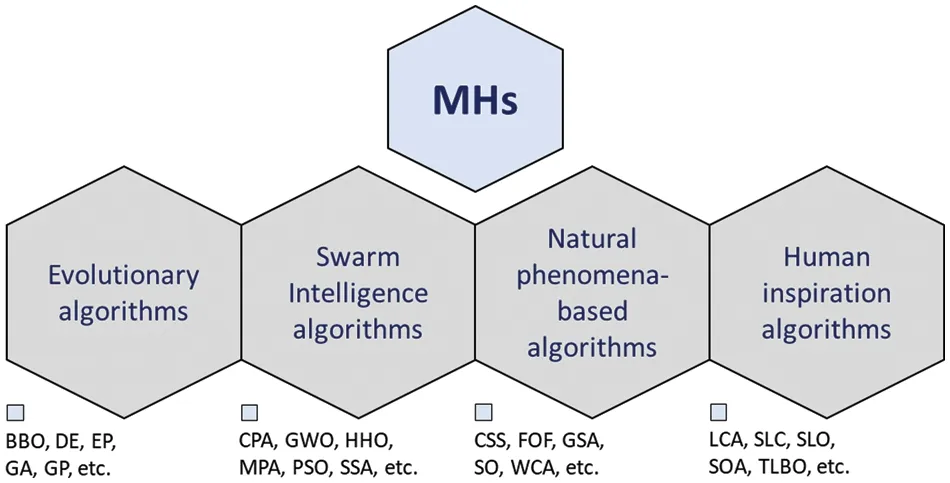
Figure 2:Classification of MHs

3.2.1 Grey Wolf Optimizer

GWO [53] offered an innovative and revolutionary algorithm for optimization based on the imitation of the grey wolves’social bahavior.In specific, GWO mimics the process that grey wolves utilize to capture their prey, along with the structure of their leadership.For the recreation of the hierarchical structure in GWO,grey wolves in four different types are assumed for every wolf pack.The leader and the most significant wolf in the pack are calledα,βandδwolves.ωwolves with the minimum responsibility are placed at the bottom of the food.In GWO,the entire hunting process can be classified as:searching,encircling,hunting,and attacking.The expression for encircling of prey is given by:

wherer1andr2are the two random vectors that are uniformly distributed[0 1];andais a parameter.When|→A|>1,the exploration of prey location is possible by diverting the search agents.Conversely,with|→A|<1,convergence of search agents can be used to achieve exploitation.The hunting process in GWO can be mathematically modelled as:

In GWO,E&E are handled using parameters →aand →C,in which the parameter →ais decreased from 2 to 0.

3.2.2 Enhanced GWO

In standard GWO,exploration is allowed on the primary phase of the iterations and exploitation on the second phase.However, this approach ignored the importance of striking the appropriate balance between the two activities in order to arrive at a close approximation of the global optimum.Thus,to solve the problem,Joshi and Arora[27]proposed EGWO,in which the →awas set to be random between[0,1],and hence,the →asearch agents were modified.According to the study of Joshi and Arora[27],the hunting mechanism is given by:

3.3 Hybridization Steps of ELM and MHs

In the last decade,numerous MHs have been utilized extensively to adjust the learning parameters of many ML models in order to improve their performance[64–66].The combination of MLAs with MHs helps in the search for the exact global optimum.This is accomplished by improving the accuracy of the results.Due to the use of MHs,the search space has been reduced to a global optimum.In the case of hybrid ELM modelling,MHs update weights and biases of ELM iteratively and offer optimal values that are then used to estimate the intended output.Notably,the activation function and hidden neuron numbers(NH)play a significant role during the model construction;therefore,they should also be selected carefully during hybridization.In addition,different MH parameters,such as swarm size(NS),maximum epoch count(tmax),and upper and lower bounds(ubandlb)should also be designed sensibly for constructing the optimum hybrid ELMs.Six MHs,viz.,GWO,PSO,HHO,SSA,MPA,and CPA, were used in the current research to develop hybrid ELMs for the purpose of predicting the CS of MK-contained materials.Additionally,EGWO was used to construct a high-performance hybrid model called ELM-EGWO.Fig.3 illustrates the steps of hybrid ELM modelling in predicting CS of MK-contained cemented materials.

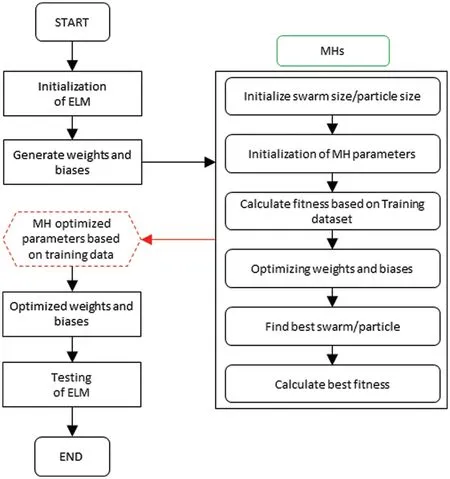
Figure 3:Flow chart of computational modelling

4 Data Description and Modelling

4.1 Data Description

In past studies, researchers focused more on making models that were easy to use and could predict the properties of concrete and cement mortar.However,they often overlooked how important it was to have a good database for making predictions.The model’s accuracy can be checked by looking at a database with enough good data.In this study, a large amount of data was acquired from Huang et al.[10]and used to predict the CS of MK-contained cemented materials.There are five influential parameters including M,MK/B,W/B,SP,and B/S,and the CS of MK-contained cemented materials is the output variable.Literature has shown that these parameters have a substantial effect on the CS.Descriptive particulars are presented in Table 1.

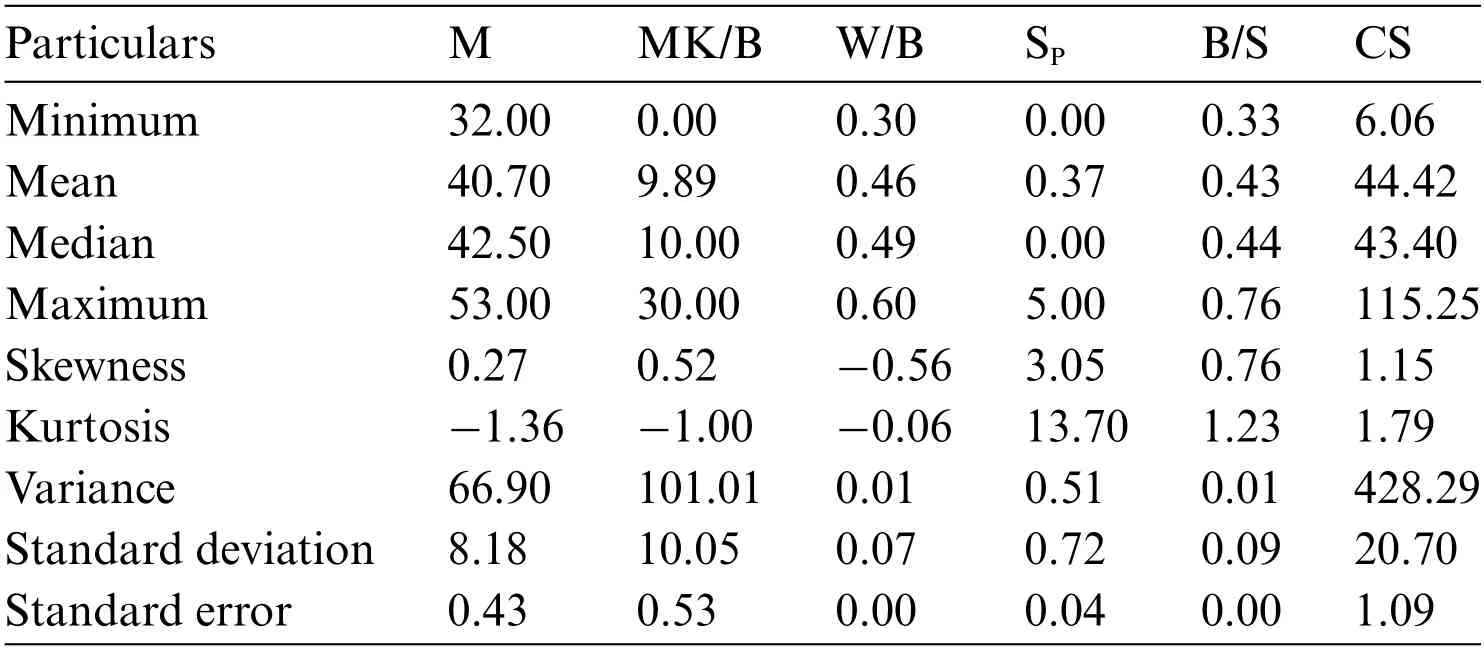
Table 1: Descriptive particulars of the collected dataset

According to Table 1,M varies between 32 and 53 with a high variance of 66.90.The parameters MK/B,W/B,and B/S scatter in the range of 0 to 30,0.30 to 0.60,and 0.33 to 0.76,respectively.the SPcontent varies between 0%and 5%.The variance of MK/B and CS is 101.01 and 428.29,respectively,which is considered to be very high.The parameters (viz., M, MK/B, and W/B) with -ve Kurtosis indicate that these variables are not uniformly distributed.Similarly, The parameters (viz., SP, B/S,and CS) with +ve Kurtosis also indicate that they are not uniformly distributed.According to this information,it is seen that the gathered records have a wide range of experimental observations and hence, can be considered useful for the estimation of CS of MK-contained cement-based materials.To illustrate the data range,frequency distribution histograms(see Fig.4)and correlation matrix(see Fig.5) are also presented.From the correlation matrix, it is seen that the association between the influential variables and the CS is scattered between–0.56 and 0.32,which is very low.The maximum correlation is -0.56 between M and CS whereas the minimum correlation is 0.025 between MK/B and CS.

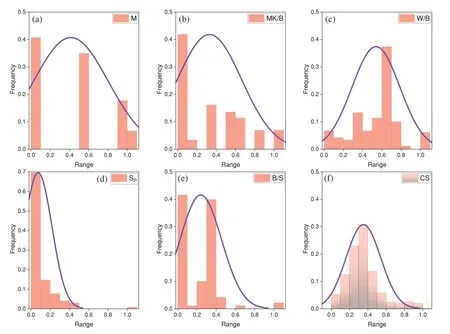
Figure 4:Frequency distribution histograms of input and output variables

Figure 5:Correlation matrix

4.2 Data Processing and Analysis

To model the CS of MK-contained materials,3 different combinations of input parameters,viz.,Case-1(C1),Case-2(C2),and Case-3(C3),were explored.For this purpose,sensitivity analysis(SA)based on the Cosine Amplitude method[1,28]was conducted.Initially,the strength of relation(RS)between the output and input variables was determined and arranged in descending order.The input parameters were then ranked between 1 and 5(there are a total of five input parameters)based on their RSvalues.The RSvalue and rankings for three combinations are presented in Table 2.It is seen that M has the highest strength(RS=0.7462),followed by B/S(RS=0.7186),W/B(RS=0.6887),MK/B(R2=0.6265),and SP(RS=0.4391).In this work,the parameters,i.e.,M and B/S were considered in Case-1.These two inputs have a high RSvalue(range from 0.7462 to 0.7186)and are thus taken into account in this combination.In Case-2,parameters with RS≥0.60 were considered.All the parameters were considered in Case-3.Notably,although there are no criteria or standards for selecting different input combinations according to RSvalue,it is up to the researchers’discretion and the type of tasks to be explained.In the current research,3 distinct ranges,i.e.,0.7462 to 0.7186,0.7462 to 0.6265,and 0.7462 to 0.4391,were investigated.

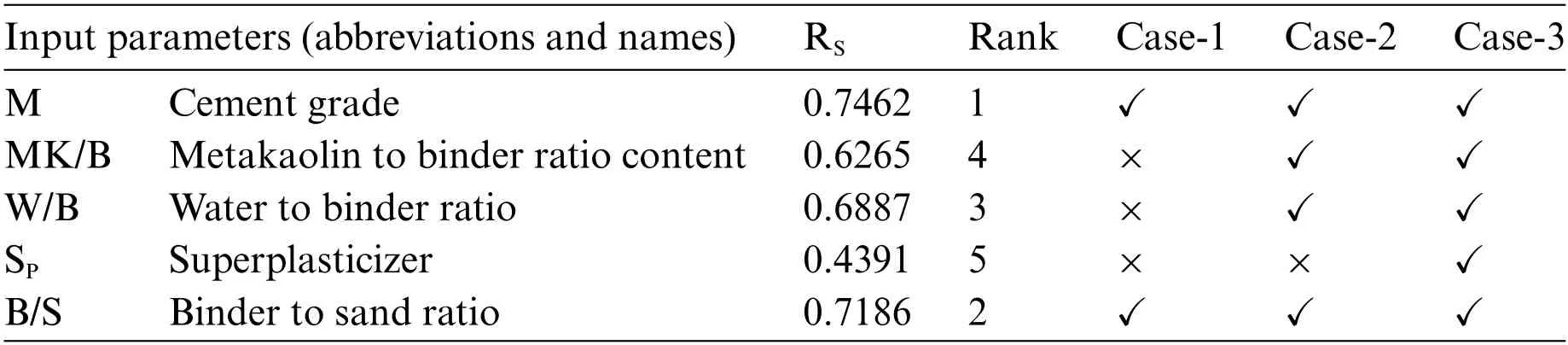
Table 2: Details of RS value and input combinations

Table 3 displays the details of different input combinations considered in the present work.The details of the computational analysis are also demonstrated in Fig.6.The steps are (a) dataset collection;(b)selection of input parameters;(c)sensitivity analysis;(d)arranging input parameters in descending order based on RSvalue;(e)selection of three different input combinations(i.e.,Cases-1 to 3)based on ranking,(f)computational modelling,and(g)training and validation of hybrid ELMs.Note that,Fig.6 shows a complete flow chart for hybrid ELM modelling,however,three conventional models,such as DNN,KNN,and LSTM,were also used in this work for predicting the CS of MKcontained cemented materials.

Table 3: Details of inputs and data dimensions for all combinations

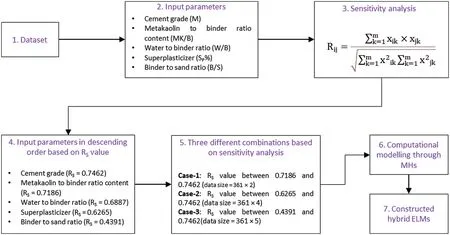
Figure 6:Illustration of computational modelling

4.3 Modelling and Performance Evaluation

It should be mentioned that data normalization is a vital activity in data-driven modelling and is frequently employed to mitigate the impacts of multidimensionality.Thus, the current research uses the min-max approach of normalization.Then the acquired records were separated into training(TR) and testing (TS) subgroups.The latter was extracted in order to estimate the trained models’outcomes against unseen samples.So, 80% (289 observations) of the collected records were used for model construction and a balance of 20% (72 observations) for validation.Notably, while there are no predefined guidelines for determining the number of samples to include in a data-driven model, the researchers’decision will be mostly determined by the nature of the tasks.Note that, a model constructed using a large sample is more likely to be accepted than one constructed from a small dataset.Thus,a 20%sample was preferred to validate the developed models.Following model development, their effectiveness was measured using multiple indices namely Adj.R2, NS, PFI, R2,RMSE, RSR, and VAF, expressed in Eqs.(15)–(21).In the domain of engineering and sciences,these are the most common indices used for the performance assessment of a data-driven model[1,28,67–70].

whereoiandare the actual and estimated outputs,respectively;nandpare the number of datasets and input parameters, respectively;ymeanis the mean of the actual output values; andAdj.R2is the adjusted value of R2.

5 Results

This section reports the performance of the developed/employed paradigms used to evaluate the CS of MK-contained cemented materials.As said above, each dataset was split into TR and TS subsets before developing the models.It should be mentioned that all of the models were constructed and corroborated with similar TR and TS subsets.Then, their results were evaluated via multiple parameters.It is noteworthy that the deterministic parameters of the MHs(viz.,NS,tmax,ub,lb,etc.)have a key role in hybrid modelling, and hence they were calibrated correspondingly.In addition,the activation function and NHof ELM were tuned appropriately.Thus,before providing the results,the next sub-section presents a complete description of the configuration of hyper-parameters and deterministic parameters and their final values in the prediction of the CS of MK-contained materials.

5.1 Parametric Configuration

To construct an optimum hybrid ELM,the NHranging between 5 and 20 was investigated.Usingsigmoidas the activation function and RMSE as the cost function, the optimal value of NHwas obtained via a trial-and-error technique.On the contrary,the deterministic parameters of MHs were also tuned in the course of simulations.The details of all the parameters for the optimum hybrid ELMs are tabulated in Table 4.The detailed approach of hybrid ELM-GWO for CS estimation is described below.

Table 4: Details of model parameters used for constructing hybrid ELMs

During ELM-GWO modelling, the ELM was set primarily and consequently the GWO was incorporated in order to optimize biases and weights of ELM.As soon as the training was completed,the final ELM-GWO structure was finalized.It is noteworthy that the GWO optimized ELM contains 16,13,and 18 hidden neurons in Cases-1,2,and 3 combinations,respectively.The numbers of input neurons were 2,4,and 5,for input combinations Case-1,2,and 3,respectively.However,the number of output neurons was 1 for all three cases.Therefore, the number of OW+Bcan be determined as 48 (2 × 16 + 16) for Case-1, 65 (4 × 13 + 13) for Case-2, and 108 (5 × 18 + 18) for Case-3 of input combinations.With NHbetween 13 and 18 and a sum of 289 training samples,the searches were carried out for global optimum at tmax=500 with NS=50 and subsequently,the OW+Bwere generated to validate the developed ELM-GWO models against each input combination.

Analogous to the ELM-GWO model, all other hybrid ELMs were developed using the same training dataset.For each hybrid ELM, the value of NHwas determined using a trial-and-error technique.However,the values of NS,tmax,lbandubwere kept constant to conduct a fair comparison between other hybrid ELMs.Other deterministic parameters of HHO, PSO, MPA, CPA, and SSA were also fine-tuned in the course of the optimization.The accelerator coefficients of PSO,i.e.,c1and c2, were respectively set to 1 and 2 in ELM-PSO modelling.In all cases, the values ofbandbwere set to-1 and+1,respectively.By employing a trial-and-error technique,the optimal configuration of these parameters was obtained,the details of which are presented in Table 4.

Fig.7 illustrates the convergence behavior for the developed hybrid ELMs for all combinations of CS estimation.It is seen that the proposed ELM-EGWO reached faster convergence and lower RMSE than other hybrid ELMs.Notably,all the ELMs were built in MATLAB 2015a environment.The computation time was recorded as ELM-EGWO=56.51 s,ELM-GWO=63.68 s,ELM-PSO=58.50 s,ELM-HHO=62.22 s,ELM-SSA=55.33 s,ELM-MPA=112.66 s,and ELM-CPA=94.93 s for Case-1;ELM-EGWO=56.98 s,ELM-GWO=57.74 s,ELM-PSO=56.97 s,ELM-HHO=66.03 s, ELM-SSA = 55.83 s, ELM-MPA = 114.94 s, and ELM-CPA = 125.74 s for Case-2; and ELMEGWO=57.73 s,ELM-GWO=57.51 s,ELM-PSO=57.19 s,ELM-HHO=64.72 s,ELM-SSA=56.02 s,ELM-MPA=114.40 s,and ELM-CPA=132.85 s for Case-3 input combinations.

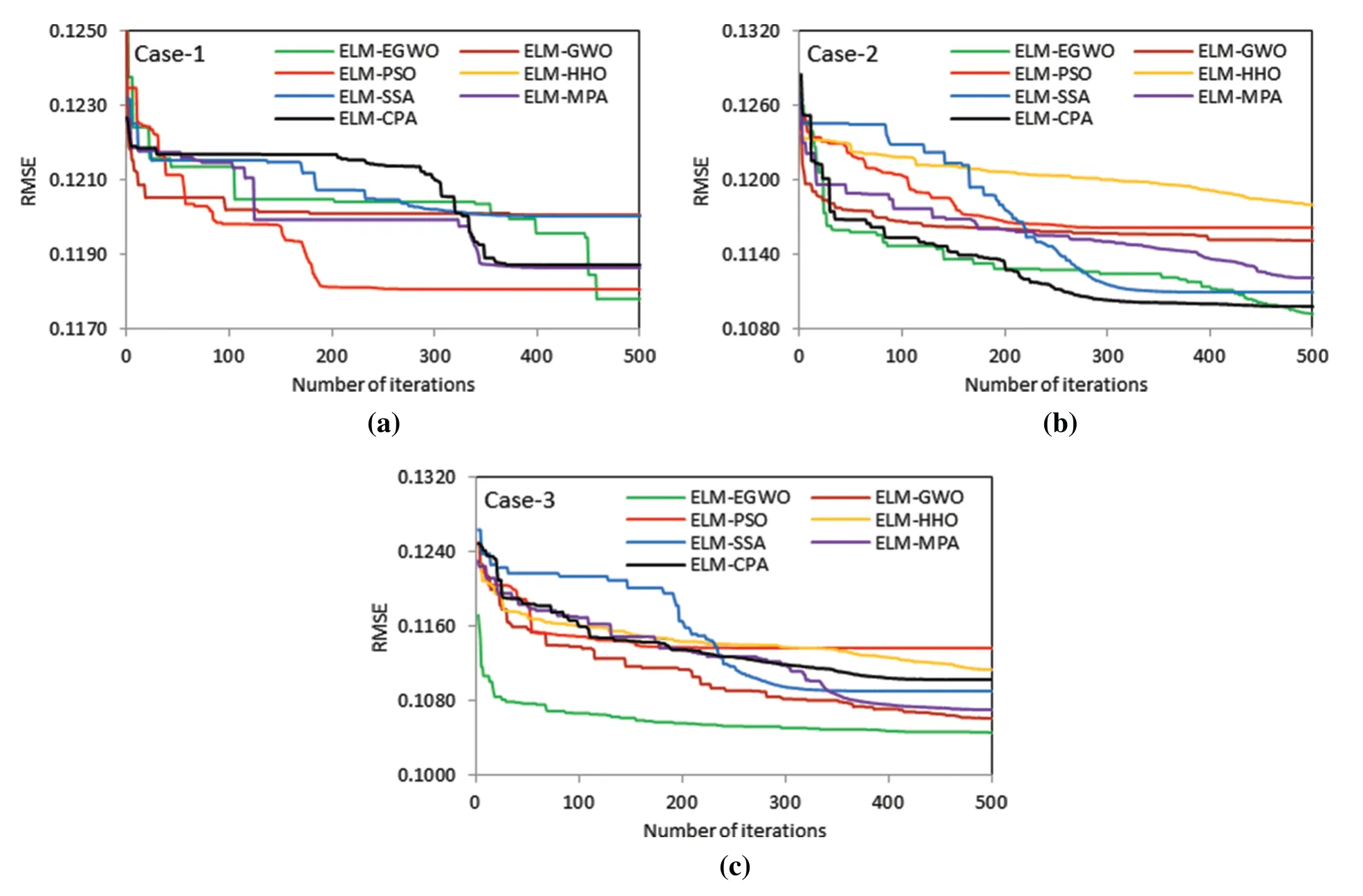
Figure 7:Convergence curves for different input combinations of hybrid ELMs

Similar to hybrid ELMs, the parameters of DNN, KNN, and LSTM were selected using a trial and error approach.The DNN structure was finalized by using mean squared error as the loss function and Adam optimizer.The final structure comprises of 5-input neurons,one output neuron,and four hidden layers with NH= 10 in each layer.Notably, in each dense layer, the ReLU was used as the activation function.For KNN,the number of neighbors was set to 5.The LSTM model was finalized using the same loss function and optimizer that were utilized during the creation of the DNN model.Thesigmoidactivation function was used in this case.The epoch number was set to 500 in the case of DNN and LSTM models.

The following sub-sections present and discuss the performance of all the constructed/employed models in the evaluation of the CS of MK-contained cemented materials.Also, a comprehensive comparison of the accuracies of models via various performance criteria is provided.In addition,the final results are visually presented and analyzed.

5.2 Model Performance

The results for all the constructed/employed paradigms for the estimation of CS of MK-contained cemented materials are given in Tables 5–7 for Cases-1, 2, and 3, respectively.Herein, the model performance along with their scores are summarized for the training subset.In accordance with the results of the R2and RMSE measures, it is evident that the proposed ELM-EGWO reached its maximum precision in the training phase.In Cases-1,2,and 3 of CS predictions,the R2are 0.5834,0.6416, and 0.7240, and the RMSE are 0.1178, 0.1093, and 0.0959, respectively.In all cases, the developed ELM-EGWO attained the highest total score of 70.The second-best model in Case-1 combination is ELM-PSO with a total score = 63, R2= 0.5814 and RMSE = 0.1181, followed by ELM-MPA (total score = 56, R2= 0.5773 and RMSE = 0.1187), ELM-CPA (total score = 49, R2=0.5768 and RMSE=0.1187),and so on(see Table 5 for other models).The second-best model in Case-2 combination is ELM-CPA with total score=63,R2=0.6375 and RMSE=0.1099,followed by ELM-SSA(total score=56,R2=0.6302 and RMSE=0.1110),ELM-MPA(total score=49,R2=0.6220 and RMSE=0.1122),and so on(see Table 6 for other models).For Case-3 combination,the ELM-GWO(total score=63,R2=0.6620 and RMSE=0.1061)and ELM-MPA(total score=56, R2= 0.6555 and RMSE = 0.1071) were determined to be the second and third-best paradigms,respectively.

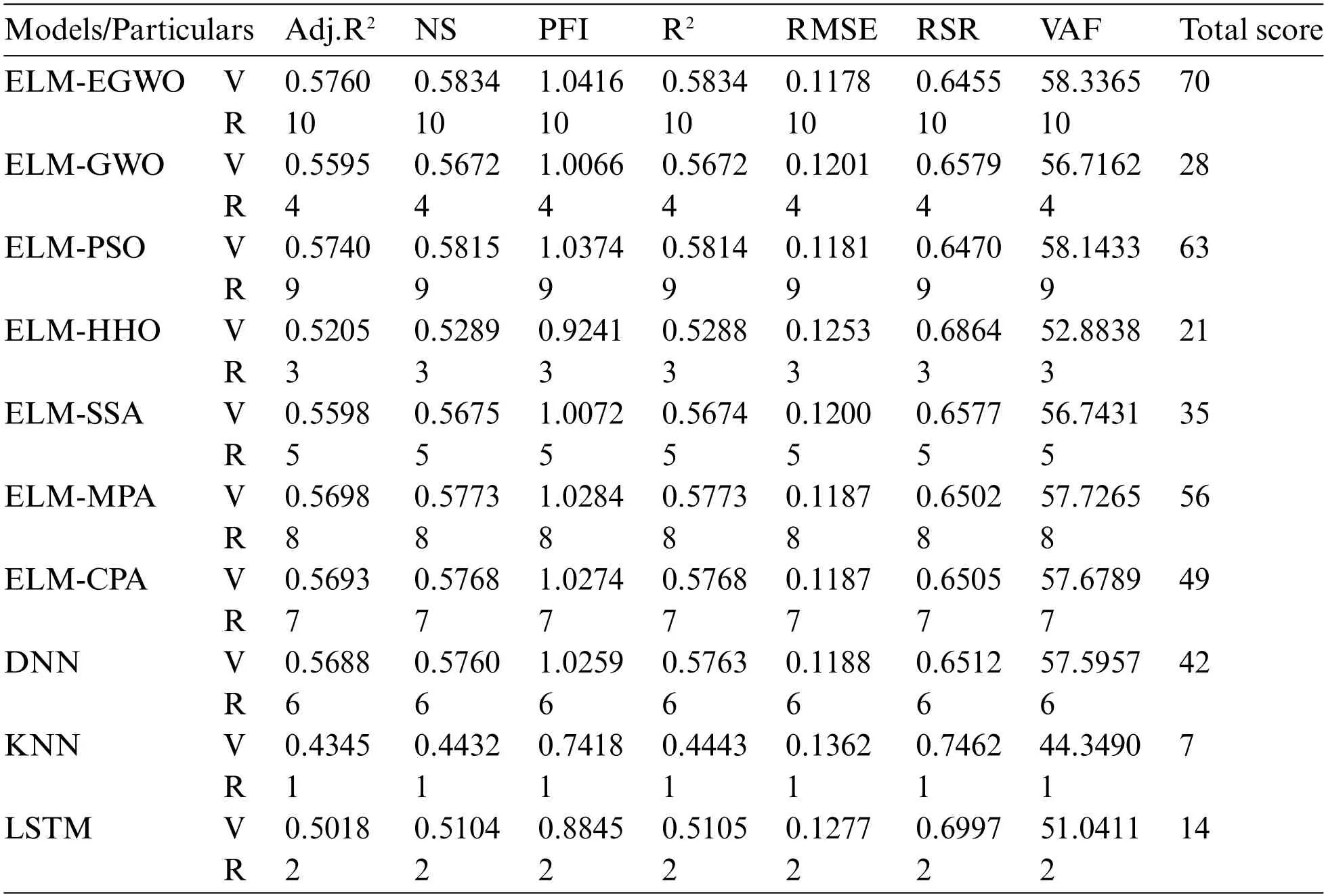
Table 5: Model performance(Case-1–TR phase)

Table 6: Model performance(Case-2–TR phase)

Table 7: Model performance(Case-3–TR phase)

For a comparative assessment,all the developed/employed paradigms were ranked(as per R2and RMSE criteria)and the details of the best three models are presented in Table 8.It is seen that the built ELM-EGWO attained the most precise estimation in all input combinations of CS prediction.Also,the R2increased significantly from 0.5834 to 0.7240,indicating Case-3 input combination is the most effective one among the three combinations considered in this work.In Case-3,the RMSE index lower than 10% (RMSE = 0.0959, i.e., 9.59%) indicates that the proposed ELM-EGWO reached a good predictive performance.According to the total score in Case-3 combination,the performance of ELMHHO(total score=7),DNN(total score=14),and ELM-PSO(total score=21)models was found to be least effective.Among the standalone models,the LSTM model shows significant performance with total score=32,R2=0.6245 and RMSE=0.1124 in the Case-3 input combination of CS estimation.To better establish the performance of the best three prediction paradigms (as per RMSE index),illustrations of scatter plots are presented in Fig.8.It is noteworthy that the performance matrices given in Tables 5–7 were determined via normalized values.

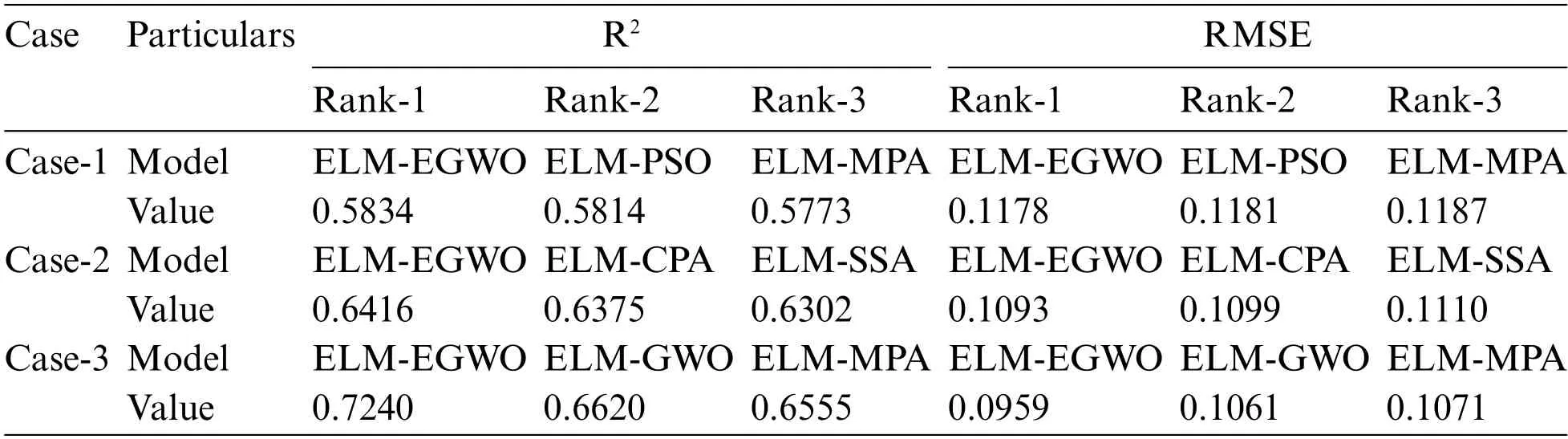
Table 8: Best three models based on R2 and RMSE criteria(TR phase)

After training the models on the same dataset, the testing subset was employed to corroborate them for all three input combinations in CS prediction.The model performance for the testing subset with normalized output values is given in Tables 9–11, respectively, for Cases-1, 2, and 3 combinations.Notably,the results of the testing subset were utilized to validate the estimation ability of the developed/employed models.According to the results,The constructed ELM-EGWO achieved the maximum precision in all cases of CS prediction,with optimal outcomes of R2=0.6751 and VAF=64.5864(Case-1),R2=0.7964 and VAF=78.5611(Case-2),and R2=0.8233 and VAF=81.8112(Case-3).In all cases,the developed ELM-EGWO attained the highest total score of 70.

The second-best model for Case-1 combination is ELM-MPA with total score=63,R2=0.6743 and RMSE=0.1284,followed by ELM-CPA(total score=56,R2=0.6740 and RMSE=0.1285),ELM-PSO (total score = 49, R2= 0.6704 and RMSE = 0.1290), and so on (see Table 9 for other models).The second-best model for Case-2 combination is ELM-CPA with total score = 63, R2=0.7677 and RMSE = 0.1081, followed by ELM-MPA (total score = 53, R2= 0.7456 and RMSE =0.1119),ELM-GWO(total score=52,R2=0.7452 and RMSE=0.1113),and so on(see Table 10 for other models).For Case-3 combination,the ELM-GWO(total score=63,R2=0.7165 and RMSE=0.1173)and ELM-MPA(total score=56,R2=0.7071 and RMSE=0.1184)were determined to be the 2nd and 3rd-best paradigms, respectively.Analogous to training results, all the developed/employed models were ranked for the testing subset,and the details of the top-three paradigms(as per R2and RMSE values)are presented in Table 12,from which it is understood that the ELM-EGWO reached the most precise prediction in all cases of CS estimation.In the testing phase, the proposed ELMEGWO led to better results in all cases,which indicates that EGWO acts better than the standard GWO when it comes to the prediction of CS of cemented materials containing metakaolin.The scatterplots in Fig.9 illustrate the top three performing models(as per RMSE index)for each of the three input combinations.

Table 9: Model performance(Case-1–TS phase)

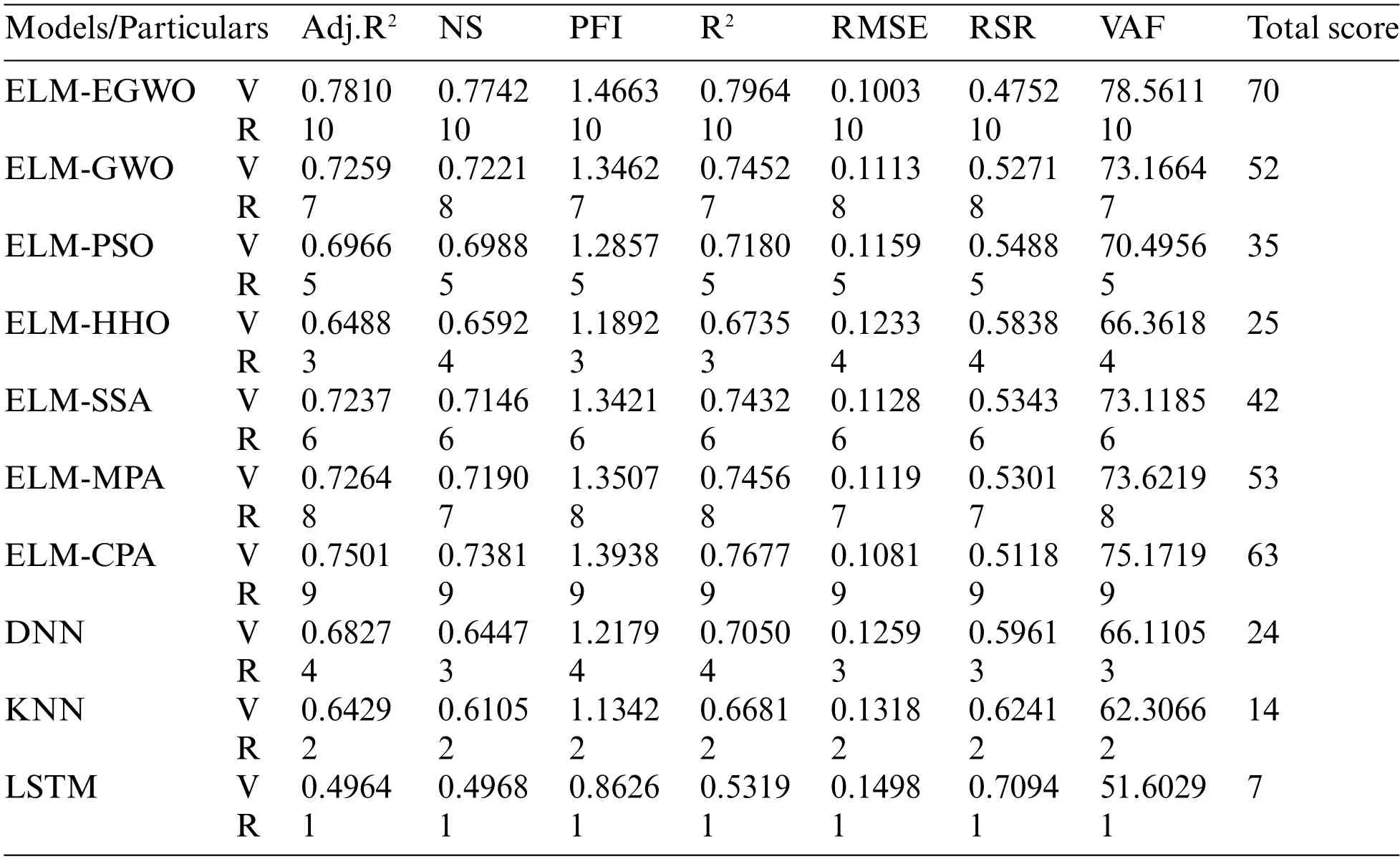
Table 10: Model performance(Case-2–TS phase)

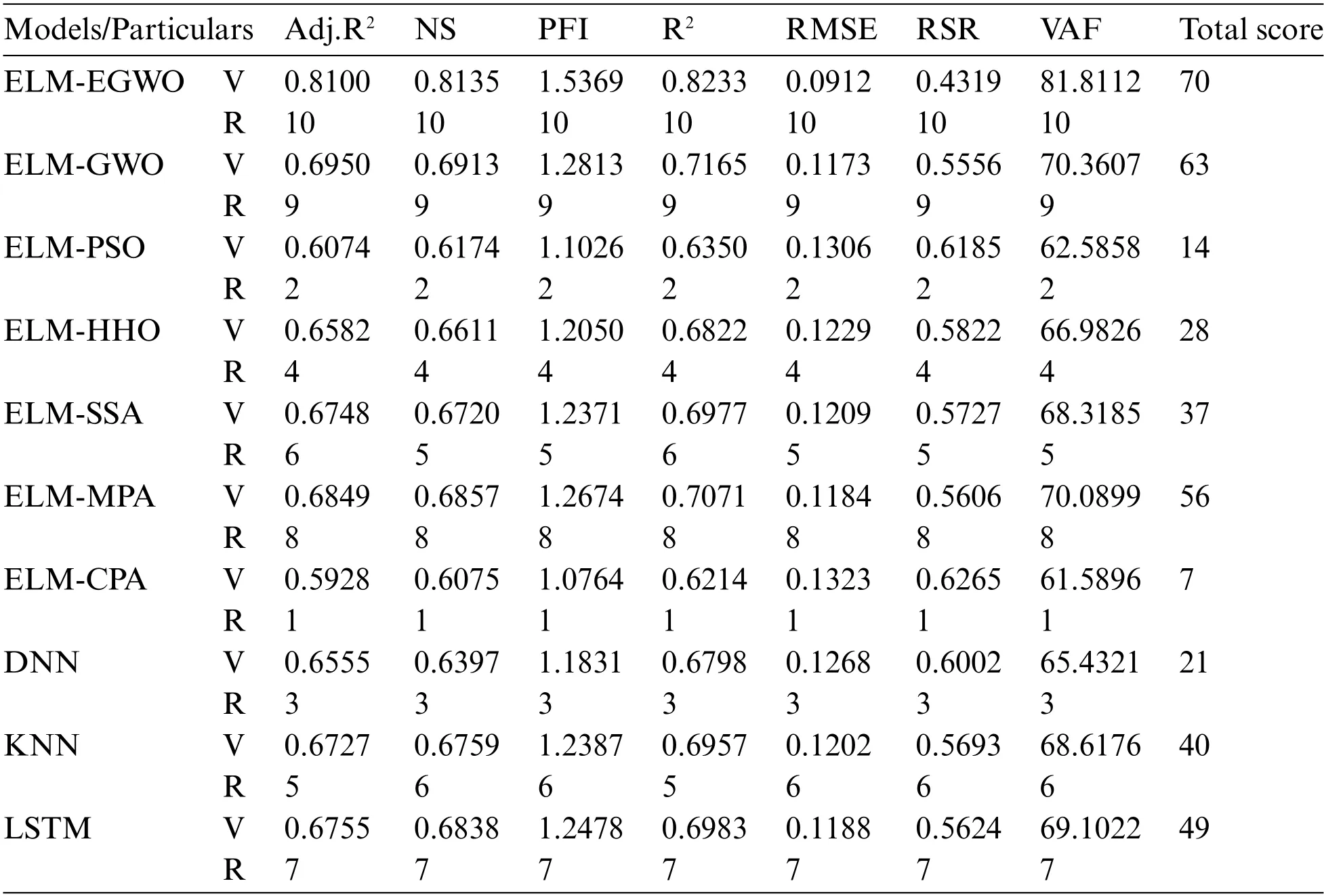
Table 11: Model performance(Case-3–TS phase)

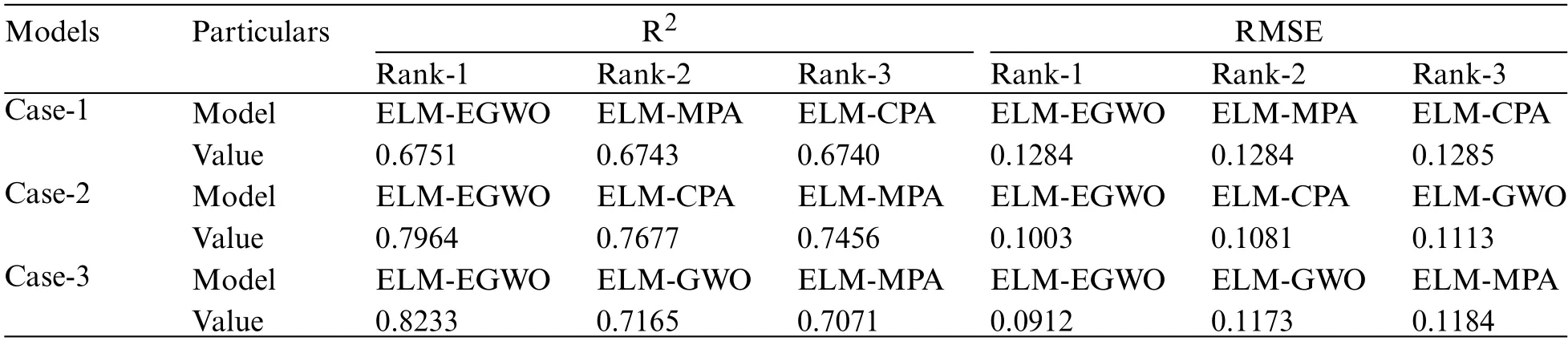
Table 12: Best three models based on R2 and RMSE criteria(TS phase)

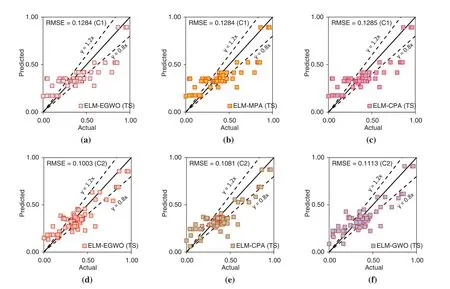
Figure 9: (Continued)

5.3 Visual Interpretation of Results

In order to spot trends, patterns, and other insights, it is always preferable to offer a visual description of the gathered information rather than reading raw reports/data.Raw data is visualized using graphical representations,allowing users to easily explore the data and reveal profound insights.It permits one to grasp information quickly and effectively.Thus, to investigate the generalization ability of the generated/employed paradigms, visual interpretations of results are presented and discussed in this sub-section.

In this work,the performance of the developed/employed paradigms was examined using index scoring and Taylor diagram [71].The model performance for the testing subset is only reported in this sub-section.Taylor diagram is a 2-D graphic that depicts the associations between the actual and expected variables in terms of three different matrices.In this figure,a model is usually depicted by a point, which should match with the point of reference for a perfect predictive model.On the other hand,during index scoring,the notion of rank analysis was utilized to rank the models based on performance matrices.All of the performance indicators were first transformed into%precision terms against each index and then ranked from 1 to m,where m(in this study m=10)is the number of prediction models under consideration.On the basis of R2index,the accuracy of the developed models(for Case-3 input combination) was found to be ELM-EGWO = 82.33%, ELM-GWO = 71.65%,ELM-PSO=63.50%,ELM-HHO=68.22%,ELM-SSA=69.77%,ELM-MPA=70.71%,ELM-CPA= 62.14%, DNN = 67.98%, KNN = 69.57%, and LSTM = 69.83%.Therefore, they can be ranked by assigning a maximum rank of 10 to the model with the greatest R2value and a rank of 1 to the model with the poorest R2value.The ELM-EGWO model received a score of 10 for having the highest accuracy of 82.33% (R2= 0.8233), while the ELM-CPA model received a score of 1 for having the lowest accuracy of 62.14%(R2=0.6214).The same steps were followed for other indicators.It should be noted that a model with the highest score of 70 (i.e., total number of models considered × total number of indices=10×7)is deemed extremely accurate.Figs.10 and 11 represent the Taylor diagram and index scoring,respectively.The correctness and degree of inaccuracy of the employed/constructed models can be deduced easily from these figures.

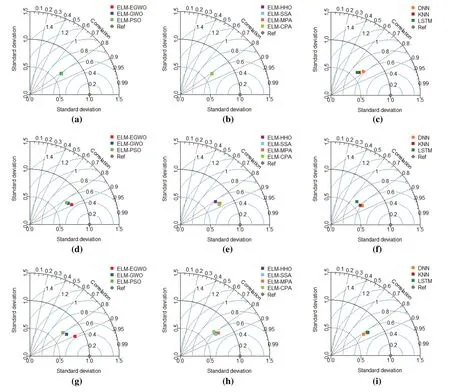
Figure 10:Taylor diagram for the TS subset:(a–c)C1,(d–f)C2,and(g–i)C3 of CS prediction

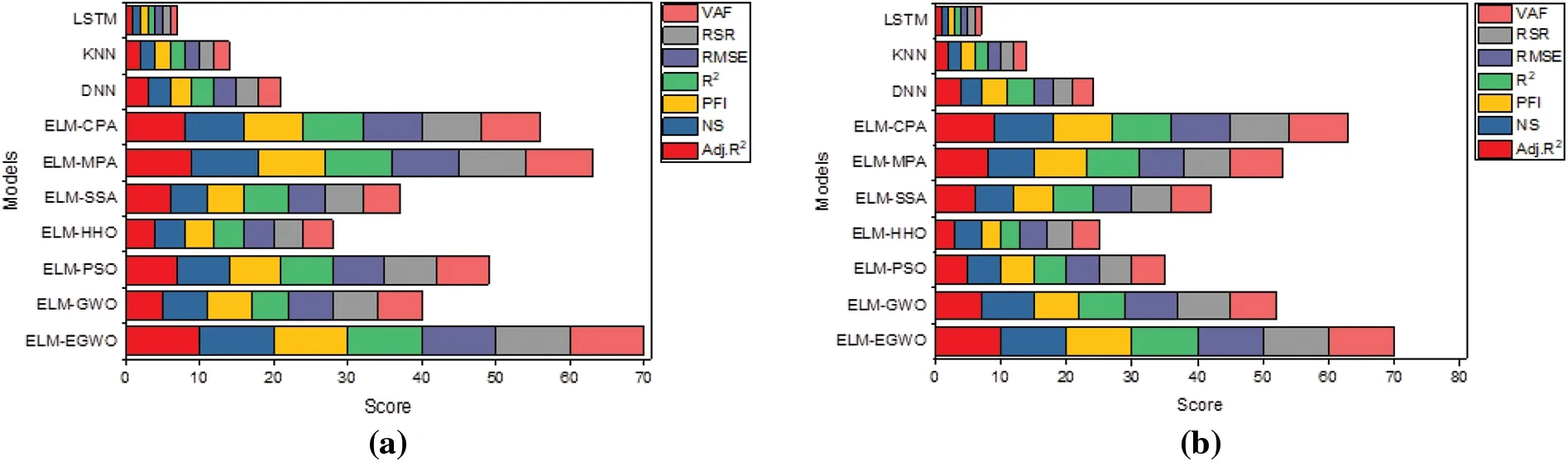
Figure 11: (Continued)

5.4 Statistical Testing

Notably, quantitative estimation of a data-driven model’s results is an important criterion for assessing its reliability in forecasting the desired output [72].Therefore, uncertainty analysis (UA)was conducted in this work to undertake the quantitative evaluation of the prediction models’errors.Herein, the results of the whole dataset are investigated.Since there are 72 real-life records in the dataset, it is significant to compare the results of predictions to see how reliable the developed/employed models are.In UA, the error (εi) between the estimated (i) and actual (oi) outputs was calculated usingεi=|oi-i|.Subsequently,the standard deviation(SD)and the standard error(SE)can be obtained as:

wherenrepresents the observation count.Subsequent to the estimation of the SD and SE,the margin of error(ME)was determined at a 95%confidence interval in order to estimate the width of confidence bound(WCB).Afterward,theub,lb,and WCB values were determined as follows:

Note that, WCB represents a range of errors in which approximately 95% of the data reside.Table 13 reports the UA results for all four input combinations of CS prediction.One can evaluate the model performance based on the WCB value presented in Table 13.It is noteworthy that smaller WCB represents higher certainties,i.e.,the model is subjected to a smaller error level,and it can predict with higher precision.In accordance with the UA results,ELM-EGWO recorded the minimum WCB and mean absolute error(MAE)values of 0.0434 and 0.0891,0.0306 and 0.0762,and 0.0286 and 0.0678,respectively,in Cases-1,2,and 3 combinations.In addition,smaller quantities of ME,SE,and SD are rendered as higher reliability for ELM-EGWO compared to the other suggested models.For a quick assessment, all of the models were ranked by their WCB value.MAE and SD were used to rank a model with the same WCB value.It is seen that the proposed ELM-EGWO is the most reliable model(secured first rank)in all cases.A comparison of the developed hybrid ELMs with DNN,KNN,and LSTM shows that the LSTM and DNN have the highest WCB value among all models.Nonetheless,based on the outcomes presented in Table 13,the proposed ELM-EGWO can be considered reliable in predicting the CS of cemented materials containing metakaolin.However,for a better comparison,the UA results are presented in Fig.12.

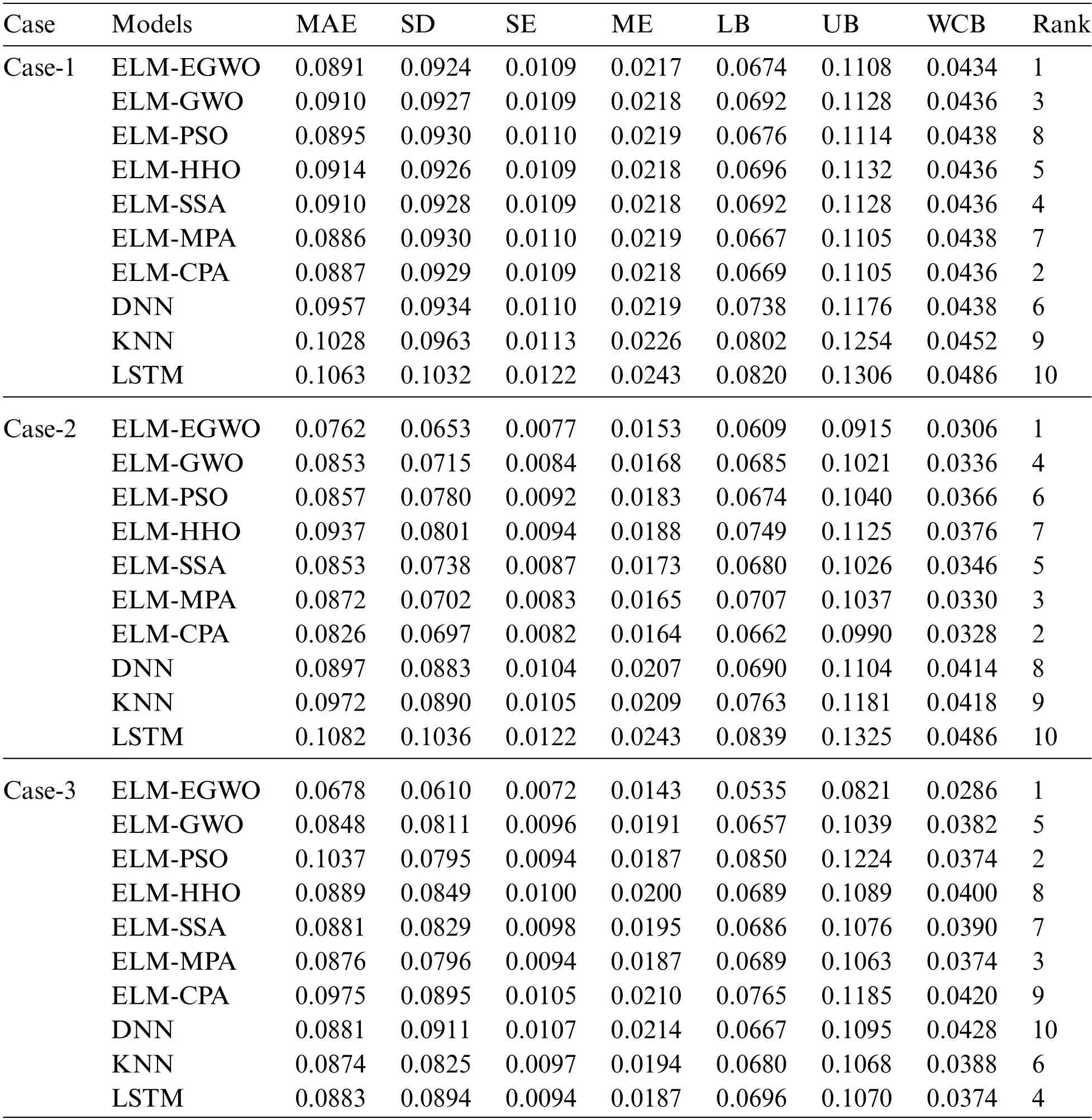
Table 13: Results of UA for all input combinations

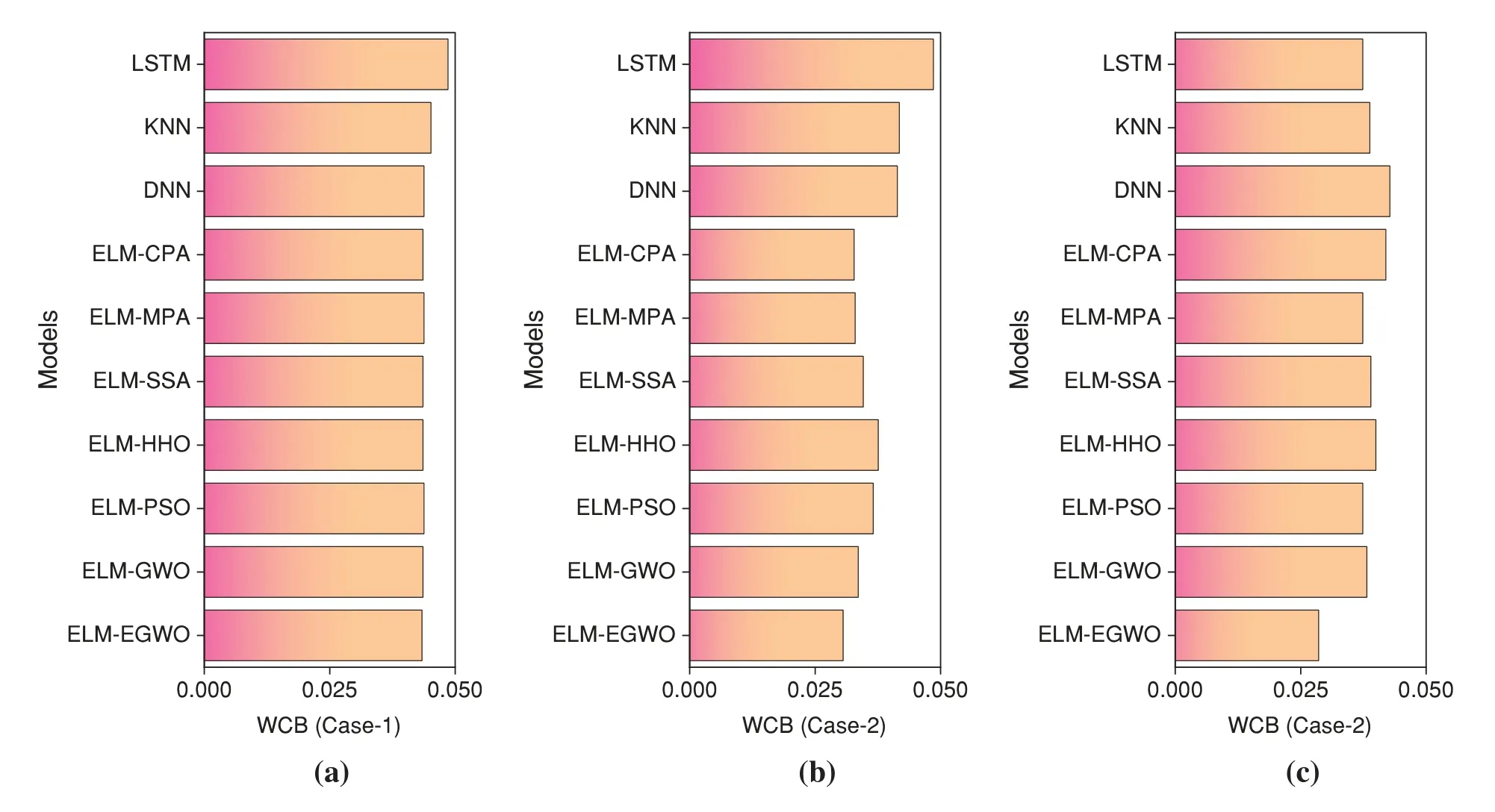
Figure 12:Bar plot of UA for all combinations of CS prediction

5.5 Monotonicity Analysis

Furthermore, the monotonicity analysis was used to test the viability of the proposed ELMEGWO model for different input parameters of MK-contained cemented materials.Notably, overfitting is a common problem encountered during the mathematical simulation of datasets.This means that a model may succeed in an excellent simulation of data used for its development and training,but at the same time predict extremely unusual behavior for other datasets.Hence, it is worth assessing the overall behavior of the optimum models with regard to their expected behavior in terms of the estimated parameter.Thus,the purpose of this investigation was to see if the proposed ELM-EGWO model is capable of developing the necessary trend between various inputs and CS.For this purpose,one input parameter was changed monotonically, while the other inputs were kept constant at their mean values(as presented in Table 1),resulting in a simulated dataset(details tabulated in Table 14).The variation of the anticipated CS with various input parameters can be identified using the ELMEGWO model.The changing range of the input parameters cannot exceed the range defined by its minimum and maximum values during the monotonicity computation, as presented in Table 1.Figs.13a–13o show the variation of the predicted CS value with all the influential variables.As can be seen,the predicted CS decreases as W/B,and B/S increase whereas the CS increases with the increase of M value.However,the value of CS rises initially and then declines when the MK/B and SPrise.These variations are consistent with the theoretical trend for the CS value against each input parameter,implying the correctness of the proposed ELM-EGWO model.

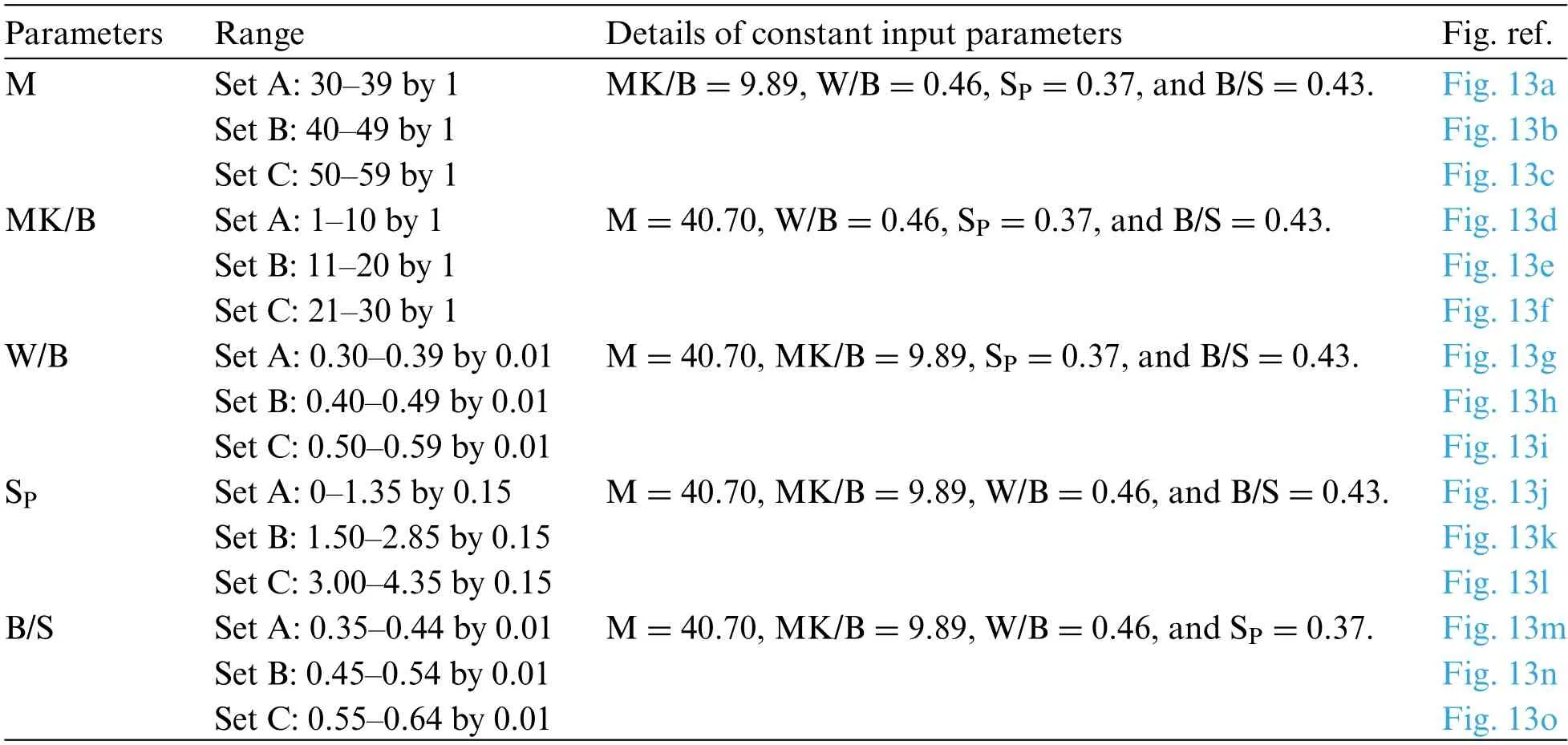
Table 14: Details of datasets for monotonicity analysis

Figure 13: (Continued)

5.6 Discussion of Results

A thorough examination of the prediction outcomes of the proposed ELM-EGWO model in estimating CS of cemented materials containing metakaolin is provided in the above sub-sections.In this work, three distinct input parameter combinations were chosen for model construction and validation.The ELM-EGWO model appears to be the most successful based on the results of RMSE,R2, and other performance metrics.The said model also attained the requisite predicted accuracy in Case-3 combination.Using UA,the reliability of the proposed/employed models was assessed.The ELM-EGWO model was determined to be most reliable in Case-3 combination(WCB=0.0286)when the produced models were evaluated using the WCB value.Note that,the uncertainty evaluation was done only based on the testing dataset because a model with higher accuracy during the validation phase is deemed more resilient and should be recognized with greater confidence.It can also be seen from the results that the Case-3 input combination provided a stronger prediction model,implying that the parameters considered in this study had a significant effect on the CS of MK-contained materials.Moreover,the results of the monotonicity analysis verify the correctness and validity of the proposed ELM-EGWO model.Based on the results of monotonicity analysis,engineers and practitioners can attain the desired CS value by adjusting the proportions of different influential parameters.However,it may be noted that the effects of different parameters presented in Fig.13 may differ during the course of manufacturing different-grade cemented materials.

6 Summary and Conclusion

This research proposes a novel hybrid model, ELM-EGWO, for estimating the CS of MKcontained cemented materials.To create and evaluate the constructed ELM-EGWO model, three distinct combinations of influencing parameters were investigated based on SA.Experimental results indicate that the developed ELM-EGWO obtained the most precise CS value when all the input parameters, i.e., combination Case-3, were considered as influencing factors.Precisely, the ELMEGWO performed better than other hybrid ELMs and standalone models in the testing phase with R2=0.6751 in Case-1,R2=0.7964,and R2=0.8233 in Case-3 combinations of CS prediction.Overall,the experimental findings show that the newly suggested ELM-EGWO model has strong potential to estimate the CS of cemented materials containing metakaolin with a high degree of accuracy and robustness.

One of the key advantages of the proposed ELM-EGWO had the highest predation accuracy,demonstrating EGWO’s superiority over the standard GWO and other MHs employed in this work.The proposed ELM-EGWO model also offers a faster convergence rate,which is a significant benefit.

In addition, the findings of monotonicity analysis will enable researchers/practitioners to design concrete by changing the mix proportions of MK and superplasticizers as per their requirements.This will lead engineers/practitioners to implement a sustainable concept without affecting the desired strength of concrete.However,the future scope might include(a)a thorough evaluation of the ELMEGWO and other hybrid ANN,SVM,and ANFIS models constructed with EGWO in predicting CS of MK-contained concrete and cemented materials;(b)a comparison of the proposed ELM-EGWO to other hybrid models constructed with evolutionary and physics-based MHs,and(c)implementation of shapley additive explanations(SHAP)methods or partial dependency graphs to obtained optimized results of parametric analysis.Nonetheless,as per the authors’knowledge,this is the first research to estimate the CS of cemented materials containing metakaolin using a hybrid ELM paradigm created with an enhanced version of an SI algorithm.

Acknowledgement:None.

Funding Statement:This study is supported via funding from Prince Sattam Bin Abdulaziz University Project Number(PSAU/2023/R/1445).

Author Contributions:The authors confirm contribution to the paper as follows: study conception and design:A.B.;data collection:A.B.;analysis and interpretation of results:A.B.;draft manuscript preparation:A.B.,R.K.S.,M.A.,S.A.A.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:The details of employed dataset are mentioned in the manuscript.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.