含粗骨料膏体输送管道磨损机理及参数优化
常英杰,吴爱祥,阮竹恩,3,王贻明
(1.北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京,100083;2.北京科技大学 土木与资源工程学院,北京,100083;3.北京科技大学 顺德创新学院,广东 佛山,528399)
随着国家对矿山环境保护的重视,充填采矿法被越来越多的矿山作为主要采矿方法,而管道输送作为充填采矿法的关键技术之一,对整个充填系统的安全和稳定起决定性作用[1-2]。
随着充填技术的发展,充填料浆浓度逐渐提高,高浓度充填料浆是由固体粗颗粒、胶凝材料和水等组成的复杂悬浮体系,在管道输送过程中,由于高浓度充填料浆中含有较多的固体粗颗粒,在管道输送过程中往往会使管道产生一定磨损,随着管道磨损的问题日益突出,因此,众多学者针对充填料浆的管道磨损(见图1)展开了研究。

图1 管道磨损Fig.1 Pipe wear
针对充填料浆的管道磨损机制,众多学者对充填料浆的组成(如固体粗颗粒的尺寸、含量、硬度等)以及充填料浆的流速、浓度、酸碱度等因素展开研究。KUANG等[3]运用流体与颗粒耦合(CFD-DEM)的方法对颗粒管道输送进行数值模拟,并对相关数学模型的形成、验证和应用进行了介绍。WANG等[4]基于管道磨损回路试验系统,建立了浆料质量浓度与磨损率、浆料流量和磨损率的数学模型。CALDERÓN-HERNÁNDEZ等[5]建立了一个测试回路来模拟充填料浆管道长距离输送过程,提出了一种解释管道磨损与侵蚀、腐蚀和材料微观结构相关的机制,建立了预测管道厚度损失随输送距离变化的方法。TAKANO等[6]对304种类型的管道进行了磨损实验,分析了不同内部材料和管道倾斜度的管道磨损特征。CHUGUNKOV等[7]分析了灰渣浆结构对管道磨损的影响。UZI等[8]建立了由计算两相流动力学的一维流动模型、计算颗粒磨损的一维破碎算法(ODBA)和计算侵蚀速率的一维侵蚀模型(ODEM)组成的管道磨损模型。张修香等[9]运用Fluent对粗骨料充填料浆管道输送进行了数值模拟,发现粗骨料充填料浆管道输送数值模拟是可行的。杨天雨等[10]采用数值模拟的方法分析了质量浓度、灰砂比等对废石-风砂高浓度充填料浆管输阻力的影响。CARTER[11]建立了一种管道磨损监测系统,可以更快速地对管道磨损进行监测和跟踪。VARGA等[12]通过开展数值模拟和管道磨损试验建立了管道磨损预测模型。WU等[13]对金属矿料浆管道输送过程中的流变行为进行了分析。刘志双等[14]运用滚筒磨损实验装置分析了质量浓度、流速等因素对管道磨损的影响规律。JEONG等[15]开展了粉煤灰料浆管道磨损试验,对比了铸铁管与玻璃钢管之间的耐磨性。ZHANG等[16]探究了充填料浆垂直降落对管道的冲蚀磨损,并根据充填钻孔的高度、水平管道的长度、浆体的密度和水力坡度建立了管道磨损程度估算方法。WANG等[17-18]通过磨损试验研究了不同质量浓度、流速下充填料浆对Q345钢的磨损规律,并分析了充填料浆管道输送过程中Q345钢的磨损机理。薛希龙等[19]针对充填管道磨损风险各影响因素之间的复杂性和不相容性,建立了主客观组合权重与可变模糊集相结合的充填管道磨损风险评估方法。
管道输送磨损试验难以开展,故针对管道输送磨损的研究大多采用数值模拟的方法,但目前大多针对充填料浆的质量浓度、灰砂比、流速等因素展开研究,有关管道自身参数对磨损影响的研究较少。为此,本文作者基于Fluent数值模拟软件设计响应面试验,对不同管道参数下含粗骨料膏体充填管道磨损情况进行研究,并基于管道磨损机理对管道参数进行优化,以期为矿山管道输送系统优化提供参考。
1 充填料浆水平弯管管道输送数值模拟
1.1 RSM试验设计
为探究不同管道参数对含粗骨料膏体充填管道磨损的影响,借助Design-Export软件中的Cube工具,设计管径(管道直径)、弯管角度(管道相对走向弯曲角度)、弯径比(管道弯曲半径R与管道直径D的比值)为3种影响管道磨损的因素,分别用X1、X2和X3表示。因素水平代码如表1所示。

表1 因素水平代码Table 1 Factor level code
1.2 模型构建与网格剖分
管道模型为水平弯管,设定弯管上游长度为2 m,下游长度为4 m,网格剖分采用多区域网格剖分方式,扫掠单元边长为0.01 m,边界层数为5,过渡比为0.272,增长率为1.2,如图2所示。经网格无关性验证可知,不同管道参数下所用网格数量均对冲蚀率无影响,网格数量均大于200 000个。
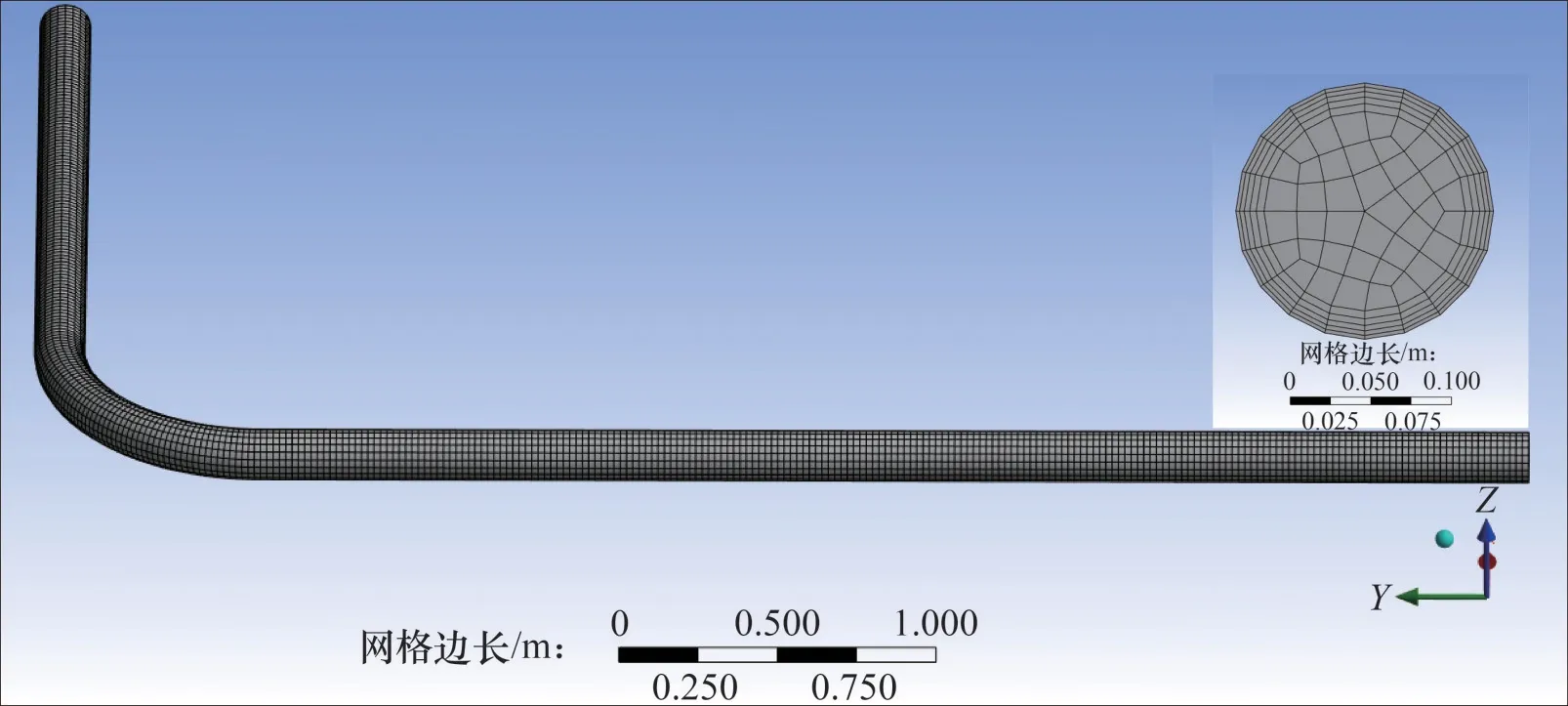
图2 网格剖分Fig.2 Grid subdivision
1.3 模型参数及边界条件
将水泥、尾砂和水的混合物视为连续相,粗骨料视为离散相,由于弯管中连续相为非理想层流状态,所以连续相模型采用k-ε模型。膏体质量分数为75%,粗骨料与尾砂质量比为1:1,连续相黏度系数为0.6,密度为1 800 kg/m3。离散相模型采用DDPM模型,根据粗骨料粒径测试结果(如图3所示),离散相直径设定为0.001~0.010 m,离散相密度为2 600 kg/m3,连续相与离散相双向耦合。入口为速度入口,离散型为Escape条件,流速为1.5 m/s,壁面条件为Reflect,出口为压力出口,离散相为Escape条件,出口压强为0 Pa,壁面粗糙度常数为0.5。
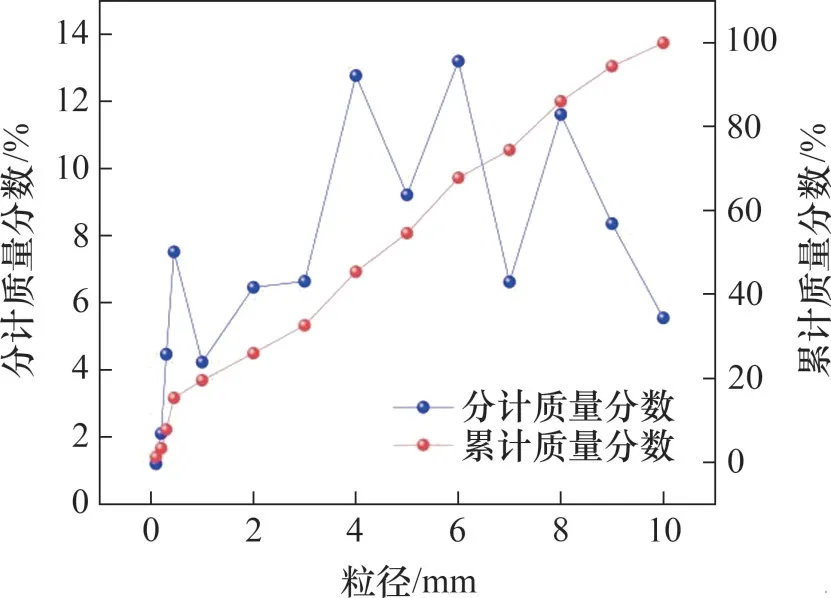
图3 粗骨料粒径分布Fig.3 Coarse aggregates particle size distribution
1.4 控制方程
1.4.1 基本控制方程
质量守恒方程表达式如下:
式中:ρ为流体密度,kg/m3;t为时间,s;ux、uy、uz分别为流体速度沿x、y、z方向的速度分量。对于不可压缩流体,ρ为常数,式(1)可写为
动量守恒方程表达式如下:
式中:p为静压,N;u为流体相速度矢量,m/s;∇为拉普拉斯算子;τxx、τxy、τxz、τyz、τyy、τyx、τzx、τzy、τzz均为作用在x、y、z方向上的应力分量,Pa;fx、fy、fz为x、y、z这3个方向上的单位质量力,N。
湍流方程表达式如下:
式中:ui为x方向的速度分量;xi和xj为空间坐标(下标i,j=1,2,3,分别代表x、y、z坐标轴,且i≠j),Pa·s;μt为湍流黏性系数,Pa·s;μ为动力黏度系数,Pa·s;Gk为层流速度梯度产生的湍流动能,J;Gb为浮力产生的湍流动能,J;k为湍流脉动动能,J;Sk和Sε为自定义参数;G1ε、G2ε、G3ε、σk、σε为经验常数,Gμ为湍流常数。经验常数可从基本湍流试验中得出,一般取G1ε=1.44,G2ε=1.92,σk=1.0,σε=1.3。
1.4.2 离散相控制方程
式中:FD(u-uq)为颗粒的单位质量曳力,N;u为流体相速度,m/s;uq为颗粒速度,m/s;ρq为颗粒密度,kg/m3;dq为颗粒直径,m;Req为相对雷诺数(颗粒雷诺数);CD为曳力系数,N;Fy为y方向其他附加力,如热泳力、加速度力、速度梯度力等,N;a1、a2、a3为常数。
1.4.3 冲蚀磨损模型
根据以往的研究[20],磨蚀与沉积模型可以较为准确地对固液两相流管道磨损结果进行预测。
式中:Rerosion为冲蚀磨损率,kg/(m2·s);mq为颗粒的质量流率,kg/s;C(dq)为颗粒直径函数;f(θ)为冲击角度函数;v为颗粒冲击速度,m/s;b(v)为速度指数函数;Aface为粒子冲击壁面的单元表面积,m2。C(dq)、f(θ)、b(v)根据壁面边界条件确定,默认情况下,取C=1,f=1,b=0。
1.4.4 壁面碰撞恢复方程
固体颗粒与壁面发生碰撞时存在能量转移和能量损失,主要表现为碰撞前后速度分量的变化[21]。通常以碰撞前后速度分量的比值衡量能量的损失情况,并将该比值定义为恢复系数。比较常用的包括FORDER等[22]提出的Non-stochastic恢复系数以及GRANT等[23]提出的Stochastic恢复系数。本文采用在计算中较为常用的Grant和Tabakoff恢复系数,其表达式为
式中:εN和εT为恢复系数;θ为冲击角度,(°)。
2 RSM-BBD试验结果
按照Design-Expert中的Cube工具生成的代码开展优化试验,结果如表2所示。

表2 优化试验的编码值与结果Table 2 Coding values and results of optimization experiment
对影响因素与最大磨损率之间的关系进行多元回归拟合,得到响应曲面函数,如式(8)所示,同时,对响应面回归函数进行检验,相关系数R2=0.99,假设检验参数P小于0.000 1,说明响应面回归函数拟合度较好,可靠性较高。
3 结果分析
3.1 管流特性分析
3.1.1 管内流速分布
图4所示为管道内流速分布云图。由图4可以看出,充填料浆在管道中主要呈柱塞状流动,在靠近管壁区域膏体料浆与管壁摩擦对料浆产生剪切作用,导致边壁区域流速较小,而在管道中心区域膏体料浆结构稳固,加速度较大,导致中心区域料浆流速较大;在弯管区域,由于料浆与弯管外侧壁面发生碰撞,流速减小,而靠近弯管内侧料浆流速较大,经过弯管区域后料浆边壁区域受剪切作用流速减小,料浆逐渐恢复至稳态流动,最大流速区域逐渐转移至管道中心位置。

图4 流速分布云图Fig.4 Velocity distribution cloud map
3.1.2 管内压力分布
图5所示为管道内压力分布云图。由图5可以看出,由于重力作用,充填料浆沿径向表现出了明显的压力梯度,在管道底部区域,料浆受重力作用对管道底部产生压力,导致越靠近管道底部压力越大;而随着料浆距离管道出口距离的减小,出口与大气相通,相对压差为0 Pa,所以越靠近管道出口压力越小。

图5 压力分布云图Fig.5 Pressure distribution cloud map
3.1.3 管内颗粒分布
图6所示为管道内颗粒分布云图。由图6可以看出,由于设置颗粒为面入射,入口管道边壁区域网格较为密集导致,入口边壁区域颗粒分布密度较大。同时,由于重力作用,在入口阶段颗粒发生一定程度沉降,管道底部颗粒分布密度比顶部的略高;同时,由于惯性作用,在弯管区域颗粒与弯管外侧壁面发生碰撞,颗粒主要集中于弯管外侧区域;在经过弯管区域之后外侧边壁区域颗粒由于重力作用逐渐迁移至管道底部,导致管道底部颗粒分布密度比顶部的大。
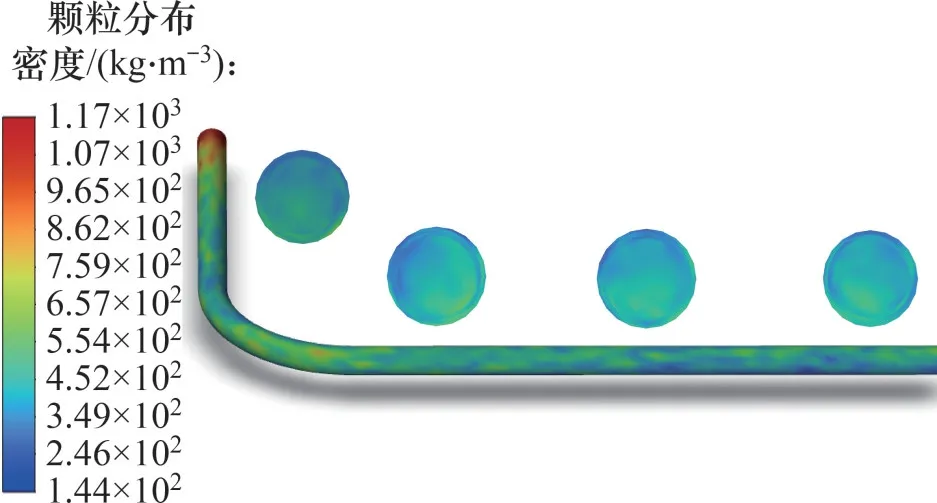
图6 颗粒分布云图Fig.6 Cloud map of particle distribution
3.1.4 管道磨损分布
图7所示为管道磨损分布云图,图8所示为颗粒轨迹。由图7和图8可以看出,在入口区域,由于入口边壁粗颗粒分布密度较大且管壁磨损较为严重,导致入口处最大冲蚀速率较大;在弯管区域,由于惯性作用粗颗粒与管道外侧壁面发生碰撞,导致管道外侧磨损较大;在经过弯管区域后,粗颗粒逐渐向中心迁移,同时由于重力作用,粗颗粒逐渐堆积至管道底部,导致管道底部管壁磨损较为严重。

图7 管道磨损分布云图Fig.7 Pipe wear distribution cloud map

图8 颗粒轨迹Fig.8 Particle trajectory
3.2 粗颗粒受力分析
图9所示为颗粒受力示意图。由图9可以看出颗粒在流体中主要受重力G、惯性力FI、剪切阻力FV、曳力FD等作用,在弯管区域还受到壁面的反弹力FR作用。在直管区域颗粒受重力作用,当重力大于垂直方向曳力时,颗粒发生沉降,导致颗粒距管道底部较近,料浆底部浓度比顶部的大。一些专家学者[24]针对颗粒在中间柱塞流动区域内能否发生沉降这一问题,提出了相应的判别公式,如式(9)所示。

图9 颗粒受力示意图Fig.9 Particle stress diagram
式中:A为量纲一参数,可用于比较颗粒所受塑性效应与重力效应;τy为y方向的剪应力;g为重力加速度,9.81 m/s2;d为颗粒直径,m;Δρ为颗粒与流体之间的密度差,kg/m3。对于非剪切流动区域内的沉降而言,存在一个判定值YS,0.048≤YS≤0.111,当Y>YS时,非剪切流动区域内的颗粒不会发生沉降;当Y 而在弯管区域,颗粒由于惯性作用撞击在管壁上导致管壁区域颗粒集中程度较大,同时,颗粒受到壁面的反射作用,产生向中部区域迁移的趋势,在经过弯管区域后颗粒逐渐恢复为原始的分布状态。在颗粒之间还存在范德华力、静电力以及水合力等,其中颗粒间作用主要受范德华力和水合力影响,静电力对颗粒影响较小。 3.3.1 单因素影响 将Design-Expert中数据导入Origin软件中进行处理。图10(a)所示为管径X1与最大磨损速率的关系。由图10(a)可以看出,当弯管角度为90°、弯径比为4时,随着管径的增加,颗粒活动空间增大,碰撞减小,最大磨损速率逐渐降低;图10(b)所示为弯管角度X2与最大磨损速率的关系。由图10(b)可以看出,当管径为160 mm、弯径比为4时,弯管角度增加导致颗粒与管壁碰撞加剧,最大磨损率逐渐增加;图10(c)为弯径比X3与最大磨损速率的关系图。由图10(c)可以看出,当管径为160 mm、弯管角度为90°时,弯径比的增大对管道输送有促进作用,随着弯径比的增大,颗粒与壁面碰撞角度逐渐减小,最大磨损速率逐渐减小。 图10 参数模型单因素对最大磨损速率的影响Fig.10 Influence of single factor of parameter model on maximum erosion rate 3.3.2 交互影响 图11所示为响应因素交互作用等高线图,表3所示为模型方差分析。由图11和表3可以看出,对最大磨损速率的影响由大到小依次为管径、弯径比、弯管角度。图11(a)所示为管径和弯管角度的交互影响。由图11(a)可以看出,管径对最大磨损速率的影响大于弯管角度的影响,随着管径的增加,最大磨损速率对弯管角度的敏感度逐渐增大,这主要是因为管径增大导致颗粒自由活动空间增加,颗粒惯性增大,其对弯管壁面碰撞强度增大。图11(b)所示为管径和弯径比的交互影响。由图11(b)可以看出,管径对最大磨损速率的影响大于弯径比的影响,随着管径的增加最大磨损速率对弯径比的敏感度逐渐增大,这主要是因为随着管径增大,弯径比对颗粒与管壁碰撞面积影响增大。随着管径增加,弯径比对最大磨损速率的影响由逐渐减小变为先变小后增大,表明不同管径下使管道磨损最小的弯径比不同。图11(c)所示为弯管角度和弯径比的交互影响。由图11(c)可以看出,弯径比对最大磨损速率的影响大于弯管角度的影响,随着弯径比的增加,最大磨损速率对弯管角度的敏感度逐渐增大,这主要是弯径比增加使颗粒与弯管壁面的碰撞面积增大。 表3 模型方差分析Table 3 Response surface model analysis of variance 图11 响应因素交互作用等高线图Fig.11 Contour diagram of interaction of response factors 图12(a)~(c)所示为不同因素交互影响的响应面分析。由图12和表3可以看出,对最大磨损速率影响程度最大的为管径,而弯管角度对其影响非常小,交互影响最大的为X1X3。将响应面模型导入MATLAB中,采用目标规划算法对模型进行优化求解,如式(10)所示,其中,120≤X1≤200 mm,60°≤X2≤90°,2≤X3≤6。 图12 响应面分析Fig.12 Response surface analysis 在试验范围内管道参数最优组合如下:管径为198.05 mm,弯管角度为84.50°,弯径比为4.57,此时,最大磨损速率为0.726×10-4g/(m2·s)。 1) 运用数值模拟软件对含粗骨料充填料浆水平弯管输送过程进行模拟,发现充填料浆在管道中主要呈柱塞状流动;由于重力和惯性作用管道底部和弯管外侧颗粒浓度较大,该区域管道磨损速率较大,颗粒在流体中主要受重力G、惯性力FI、剪切阻力FV、曳力FD、壁面的反弹力FR等作用。 2) 通过RSM-BBD试验结果建立了管径、弯管角度以及弯径比与最大磨损速率的回归方程,通过单因素分析发现,管径和弯径比与最大磨损速率呈负相关,而弯管角度与最大磨损速率呈正相关。 3) 单一影响因素下,管道参数对最大磨损速率的影响程度从大到小依次为管径、弯径比、弯管角度,交互作用下管径与弯径比共同作用的影响最大。 4) 在试验设计范围内管道最优参数如下:管径为198.05 mm,弯管角度为84.50°,弯径比为4.57。3.3 RSM-BBD试验结果分析
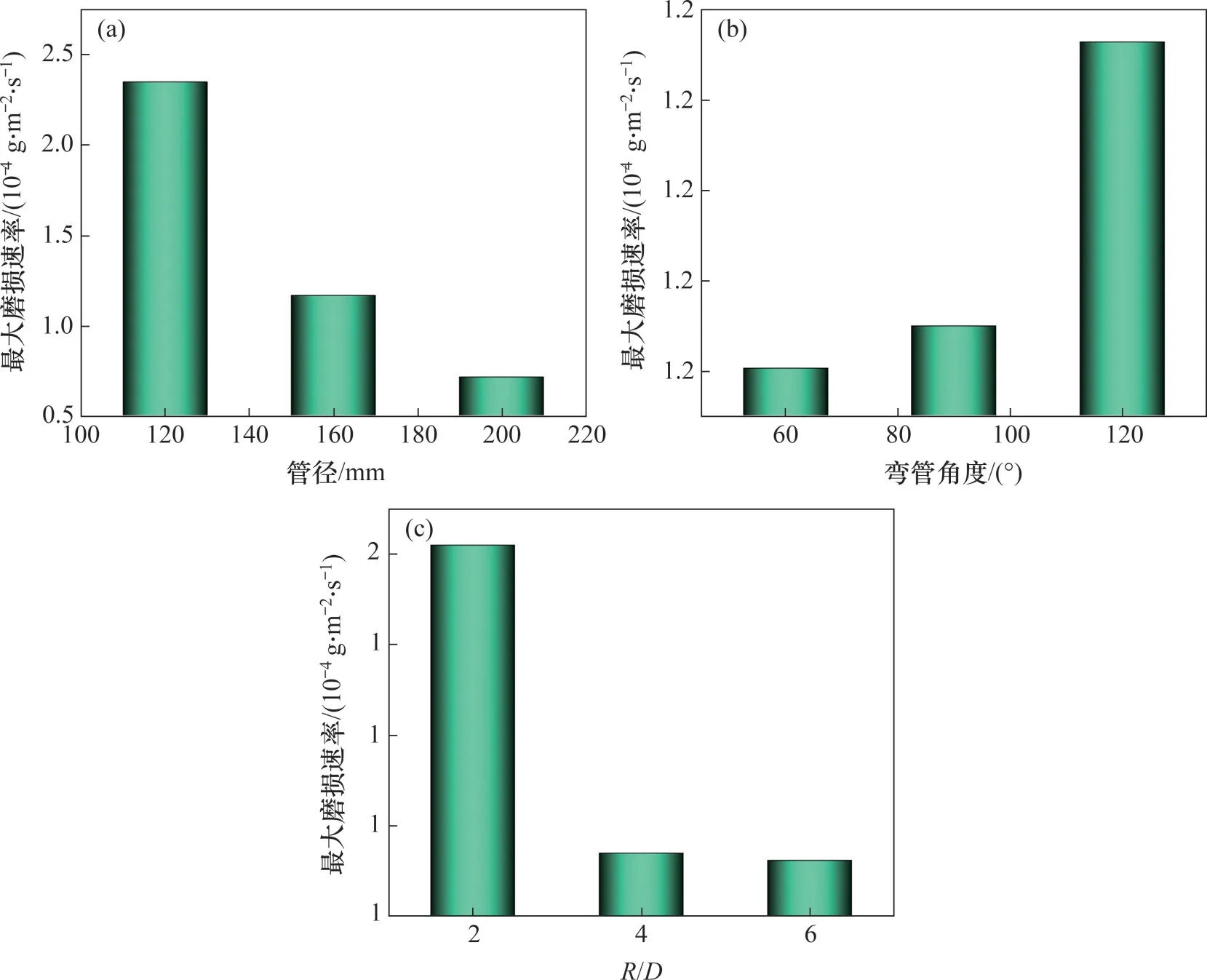


3.4 基于目标规划算法的管道参数优化
4 结论

