基于冻融循环本构的预应力对拉式挡墙的冻胀效应研究
庄妍,王赛
(东南大学 土木工程学院,江苏 南京,210000)
随着我国交通网的密度不断增加,通过山区、跨河平原区等区域的交通线路越来越多,而此类区域往往需要建造高填方路堤来保证道路的安全性,这将不可避免地增大土地的占用面积。预应力对拉装配式挡土墙由于其结构形式简单、施工简单、占地面积少等特点在高路堤结构的支护中应用较为广泛。但在季节性冻土地区,对拉式挡土墙在越冬时一方面会由于自身的冻融循环造成材料强度的折损,另一方面还会受到其后土体不同程度的冻胀作用。这种由土体冻胀所产生的水平冻胀力甚至会达到土压力的几倍乃至十几倍[1],由此作用导致的冻害往往不能忽略。
预应力对拉装配式挡土墙是由对称设置在道路路基两侧的悬臂式挡土墙与贯通路基宽度土体的预应力对拉钢筋连接而成。将预应力钢筋锚固在两侧挡土墙,再对预应力钢筋施加预应力,可以较大程度地提高挡土墙的承载力并限制挡土墙的横向位移。但由于几种材料的相互作用,挡土墙的侧向土压力分布以及在越冬时期的侧向冻胀力分布尚不明确。张宏博等[2]通过对预应力对拉式挡土墙进行模型试验,发现挡土墙侧向土压力随着墙高先增大后减小,土压力在预应力锚索处最大。宋修广等[3]用类似的试验装置测定了预应力对拉式挡土墙的墙身位移沿高度的分布,发现预应力锚杆可以较好地限制挡土墙的侧向位移。吴建清等[4]采用FLAC3D有限差分程序对预应力对拉式挡土墙进行了模拟,验证了试验结果的正确性,并研究了两根锚杆的受力情况。
针对混凝土自身的冻融循环破坏研究,POWERS[5]提出有关混凝土冻融循环破坏的静水压力学说,认为混凝土的冻融破坏是由混凝土孔隙中的水分结冰膨胀时产生的静水压力造成的。1975年,POWERS等[6]又提出了渗透压学说。冀晓东[7]在OTTOSEN[8]提出的基于三角形函数的混凝土破坏准则的基础上,结合连续损伤力学建立了混凝土冻融损伤的Ottosen强度模型;王宏业[9]将该强度模型应用于ADINA模拟软件中,模拟了混凝土经过冻融循环后的破坏特性。邹超英等[10]通过快速冻融试验得到了混凝土在经过不同次数的冻融循环后的应力-应变关系,并提出了相应的拟合公式。
针对挡土墙墙后土体因冻胀而产生破坏的现象,RUI等[11]针对L型挡土墙进行了为期3年的冻胀变形监测,总结出了L型挡土墙墙后土体发生冻胀破坏的机理,并指出了冻胀裂缝的位置。孟繁宇[12]基于室内试验探究了土体初始含水率对粗细颗粒混合土体积冻胀率的影响规律,并通过ABAQUS软件获得了季节性冻土区桩板式挡土墙的水平冻胀力分布规律。ZHU等[13]则采用孔隙率函数对土体的冻胀进行了数学描述,并将函数嵌入ABAQUS中对悬臂式挡土墙和地面在冻胀过程中的真实变形结果进行了模拟。邓青松等[14]依据实时监测数据以及冻土路基水-热耦合模型,分析了季冻区公路路基水热场阴阳坡差异。董建华[15]等为了研究季节冻土区的边坡支护结构在温度周期性交替变化时的冻融反应规律,研制了一套季节冻土区边坡支护结构冻融模型模拟系统。吴忠鑫等[16]基于FLAC3D开展了越冬基坑的冻胀力模拟,并通过正交试验探究了冻胀力的影响因素。沈宇鹏等[17]基于越冬基坑的现场观测,阐明了支挡结构所受水平冻胀力的机理。董建华等[18]依托MATLAB自行编制了水-热-力耦合分析软件,建立了墙后有无换填土2种情况下的L型挡墙水平冻胀效应计算模型,并将其与现场实测值进行了对比,验证了模型的有效性。
上述研究表明目前挡土墙的冻胀力研究还停留在常用的挡土墙类型上,对于预应力对拉式挡土墙这种新型挡土墙的冻胀研究较少,且研究冻胀力时未考虑挡土墙自身的材料破坏,因此,对拉式挡土墙的墙背冻胀力分布以及墙体位移模式尚不明确。为此,本文通过ABAQUS有限元分析软件进行对拉式挡土墙的温度场以及冻胀力模拟,研究对拉式挡土墙所受的冻胀力的分布情况以及位移,以期为北方地区该类型的挡土墙的设计提供参考。
1 冻土温度场模型
1.1 三维数值模型概况
对预应力对拉式挡土墙进行数值模拟时需要进行顺序耦合分析,即首先需要获得模型在温度场空间的分布,而后基于得到的温度场分布进行对拉式挡土墙的冻胀力分析。需要注意的是,温度场模型及网格划分应与静力场分析时的一致。本文依据哈尔滨市某一匝道路段进行建模,选取预制悬臂挡土墙的一段进行分析。图1所示为三维数值模型示意图,模型由2个相对的悬臂式挡土墙、墙间填土以及地基土组成。悬臂式挡土墙中心通过预应力筋相连,并通过施加预应力来提高承载力,其中预应力钢筋的直径为350 mm。图2所示为数值模型剖面图,图3所示为挡土墙尺寸示意图。
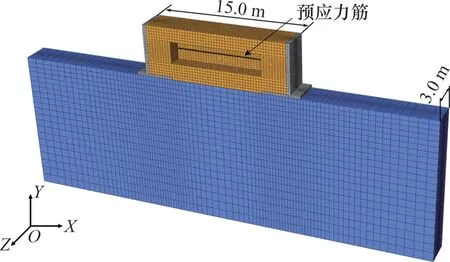
图1 三维数值模型示意图Fig.1 Diagram of three-dimensional numerical model
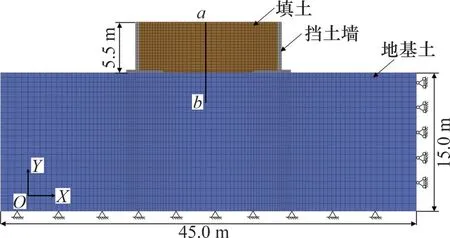
图2 数值模型剖面图Fig.2 Numerical model profile diagram

图3 挡土墙尺寸示意图Fig.3 Diagram of retaining wall dimensions
1.2 材料参数
以王晓巍[19]于2008-10—2009-09在哈尔滨市万家灌区所进行的温度观测实验结果为依据对温度场进行模拟。试验观测地具有天然的土壤冻结条件,面积达2 000 m2,可以较好地实现土体的天然冻胀。通过对比模拟结果和观测结果,可以验证温度场模拟的准确性。本文所选用的土体和挡土墙模型为各向同性传导模型,根据文献[20],材料的参数见表1。在温度场模拟时水-冰的相变过程主要通过土体在相变时释放的潜热来考虑。

表1 各层土体的参数Table 1 Parameters of soil layers
1.3 边界条件的选取
根据文献[19]中的观测结果可知,哈尔滨地区由于其海拔较低,该地区的气温和地面温度的差异较小。另外,地下温度的变化主要集中于地表注:相变潜热指土壤中的水转变为冰时所释放的热量,工程上常用334.56 J/g,本文取含水率为10%时的相变潜热。面至地下1.8 m左右,地下2.0 m后的土层温度维持在8 ℃左右。2008年11月至次年6月哈尔滨地区的地表温度分布见图4,通过对图4中温度曲线进行插值可以得到2008年11月至次年5月底的每日地表温度。首先,通过对模型施加初始温度场以及表面温度荷载得到模型2008年11月的真实温度场分布;然后,通过将插值得到的每日地表温度荷载作为边界条件施加至模型,从而实现对地表负温的施加。
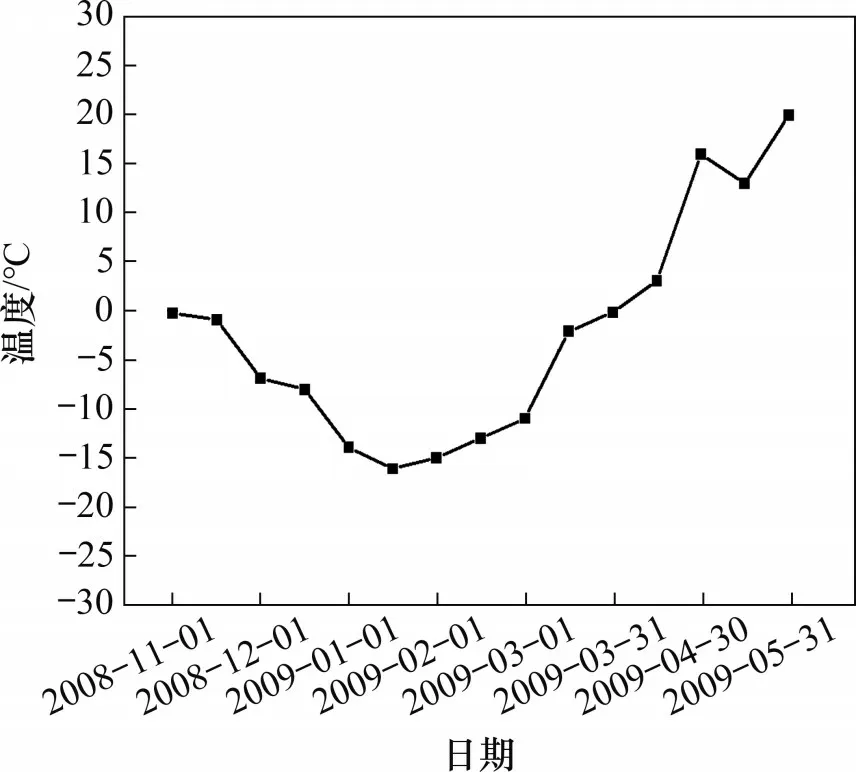
图4 哈尔滨地区地表温度分布图Fig.4 Earth surface temperature in Harbin
1.4 数值模型验证
为了验证模型的有效性,提取模型中心沿深度方向(图2中ab段)的温度与文献[19]中在哈尔滨地区所得到的实际观测值进行比较。对比分析最大冻结深度随时间的变化关系以及不同时间下温度沿深度的变化,结果分别见图5及图6。图5中,T代表自2008年11月初所经历的时间。通过对比模拟结果和实验结果可以发现,两者均具有相同的变化趋势,模拟结果和观测结果的最大相对误差不到10 %,可以较准确地模拟实际情况,因此可以认为模型的温度场模拟有效。

图5 最大冻结深度随时间的变化Fig.5 The maximum freezing depth varies with time
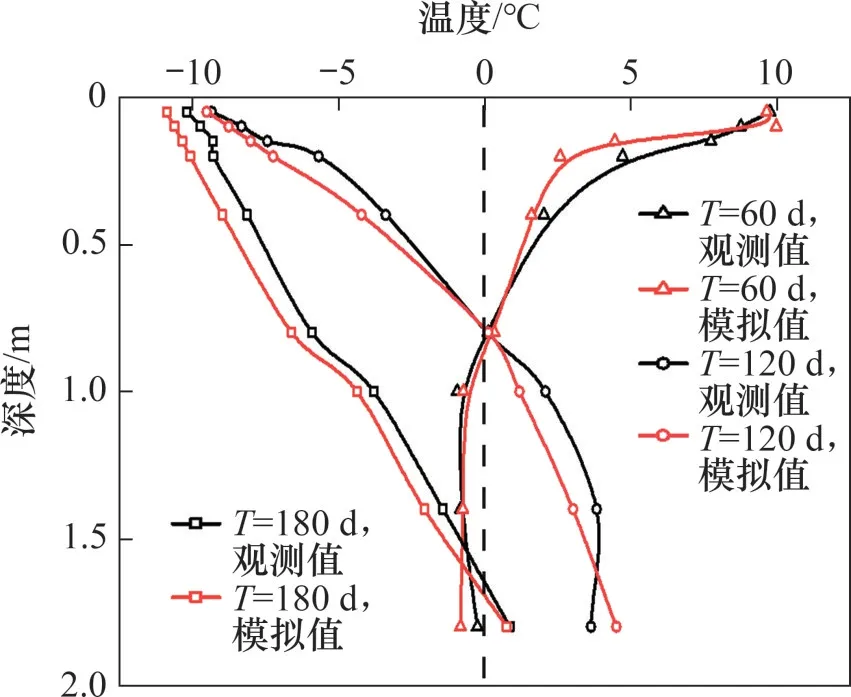
图6 不同时间下温度沿深度的变化Fig.6 Temperature changes at different time along depth
2 模型结果分析
2.1 温度场结果分析
图7所示为不同时间模型温度分布云图,由于温度场的分布呈现对称性,故本文仅选取温度场云图的1/2进行分析。图7(a)所示为模拟初始状态时温度分布情况,此时地表温度为1 ℃,地下1.8 m深度以及更深处土体温度均为8 ℃。当T=30 d时(如图7(b)所示),随着气温的降低,2008年11月末地表开始出现负温,并逐渐向下部进行传递,此时土体开始出现冻结,冻结线开始由地表面逐渐向下延伸。在T=30~90 d范围内,T=90 d时地表温度达到最低,为-14 ℃,此阶段土体的冻结区域不断变大,冻结线也不断下移。当T=150 d时(如图7(e)所示),地表温度开始由负温变为正温,土体上部开始融化,但下部由于土体内部的负温的传递,冻结深度还会继续向下偏移。当T=180 d时(如图7(f)所示),填土上部温度不断上升,导致土体逐渐向下融化,填土下部则由于下部正温土体的热传导逐渐向上融化,此时进入双向回融过程,此过程持续到2009年5月底,土体最后实现完全融化,冻胀消失。
2.2 冻结深度变化规律
为研究冻结深度的变化规律,选取沿模型对称轴ab位置的不同深度范围内的温度进行定量分析,由于中部距离挡土墙位置较远,故可认为此处的温度变化和天然单向冻结状态下的温度变化较为相似。沿深度方向每15 d记录最大冻结深度,可以得到最终的冻结深度包络线,如图5所示。通过冻结深度包络线可知,从2008年11月份开始,气温逐渐下降,地面温度也随之下降并逐渐开始结冰,呈现单向的冻结状态。这种状态一直持续到T=150 d,地表面开始融化,但土体内部负温还会继续向下传递,此时会达到最大冻结线深度(约地下1.9 m处)。之后填土开始融化,底部冻结线开始反向上升,同时,上部由于地面温度升高而下降的冻结线不断靠近。最终在T=210 d即2009年5月下旬时冻结区域完全消失,完成整个冻融过程。
2.3 冻胀类型分析
本文根据土体冻胀区域的不同将模型的温度场划为3种冻胀类型,见图8。

图8 不同冻胀类型的冻胀区域划分Fig.8 Division of frost heave area of different types of frost heave
1) 类型1。如图8(a)所示,12月初冻结区域仅为挡土墙上部的正后方土体,土体发生冻胀后,将会向上部以及侧面膨胀。挡土墙后的冻结区域可划分为水平单向冻结区域A、顶部双向冻结区B以及竖直单向冻结区域C。A区域土体在竖直方向可以自由地膨胀,但在水平方向,由于挡土墙的约束会产生水平冻胀力,此时,其对墙体的作用较小。B区域会受到挡土墙以及土体两侧负温的侵入,土体在竖向的变形不受约束,但在水平方向会由于A区域土体以及墙体的限制产生较大的水平冻胀力。C区域的负温侵入来源为挡土墙一侧,该区域等温线沿竖直方向,变形会受到4个方向的约束,这也是挡土墙水平冻胀力的主要来源。
2) 类型2。如图8(b)所示,随着冻结深度进一步延伸,会相继出现双向冻结过渡区D、底部双向冻结区E。D区域是指单双向冻结区域的过渡区,等温线呈倾斜的状态,膨胀时会受到四面的约束,因此也会产生极大的冻胀力。E区域的等温线同样呈现倾斜的状态,其会产生垂直于等温线的冻胀力。冻胀力的一部分会使挡土墙产生水平冻胀,另一部分则会产生垂直于挡土墙底部的冻胀力,即向上的冻胀作用力。
3) 类型3。如图8(c)所示,随着温度下降,冻结线进一步向下延深,冻结区域也发生变化。此时大部分的区域为顶部双向冻结,竖直单向冻结区转变为双向冻结过渡区。此时,冻胀力来源主要为顶部双向冻结区。
3 热力耦合分析
3.1 力学材料参数选择
由于本文采用ODB导入温度场对冻胀力进行分析,所以,所采用的模型与温度场分析时的模型相同,网格划分也相同,网格采用C3D8R单元。填土材料采用摩尔-库仑非线性本构。地基土由于变形较小,采用线弹性本构;挡土墙采用经过修正的混凝土塑性破坏(CDP)本构。根据文献[21]中的实验数据可得材料的力学参数,分别见表2及表3。通过定义不同负温度下土体的线膨胀系数,实现对土体的水-冰相变过程的模拟。挡土墙力学参数见表4。表4中,fb0/fc0为混凝土双轴受压强度fb0与单轴受压强度fc0的比值。

表2 材料力学参数Table 2 Mechanical parameters of materials

表3 土体材料热力学参数Table 3 Thermodynamic parameters of soil material
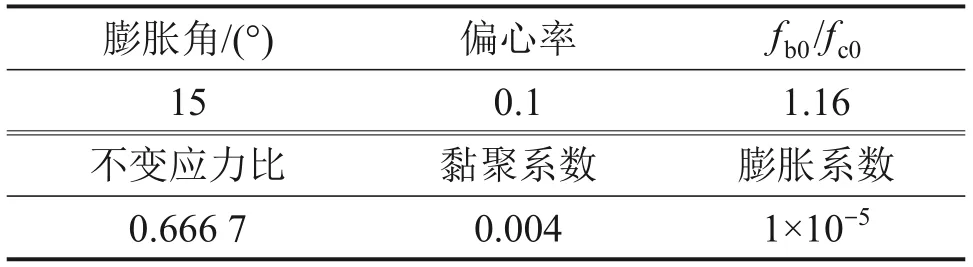
表4 挡土墙力学参数Table 4 Mechanical parameters of materials
3.2 冻融循环后混凝土本构修正
本文采用的混凝土本构为修正的混凝土损伤塑性模型[22](以下简称CDP)。CDP是基于拉、压各向同性塑性的连续线性假设所提出的,是一个连续的、基于塑性的混凝土损伤模型,其假定混凝土材料的2种主要破坏机制是拉伸开裂和压缩破碎,屈服(或破坏)表面的演变由2个硬化变量控制。
以受压为例,图9所示为混凝土单轴压缩曲线,其中,σ为应力;ε为应变。混凝土受压过程分为3个阶段:第1阶段为弹性阶段,此时混凝土没有发生塑性破坏;第2阶段为屈服应力σc0至峰值应力σcu之间的强化段,混凝土开始发生塑性破坏;第3阶段为峰值应力之后的软化段,塑性损伤不断积累。

图9 混凝土单轴压缩曲线Fig.9 Concrete uniaxial compression curve
加载过程中任意时刻的非线性应变按照下式计算:
式中:εc为任意时刻混凝土的压应变;为未受损伤的压缩非弹性应变。
压缩等效塑性应变εplc为
式中:σc为任意时刻混凝土的压应力;E0为混凝土的初始弹性模量;dc为混凝土的损伤因子,取值范围为0~1,其值代表混凝土刚度的退化程度。混凝土在单轴压缩荷载作用下的应力-应变关系为
式(3)所需要的参数需要通过混凝土单轴应力-应变关系式获得。本文所使用的混凝土本构是基于过镇海[23]提出的模型进行修正的,其本构方程如下。
在受压情况下,
其中:x=εc/εcr,εcr为混凝土峰值压应变;y=σc/σcr,σcr为混凝土峰值压应力;a为混凝土初始切线模量和峰值切线模量的比值;b为独立参数,取值范围为0~∞,当b=0时,材料发生理想的塑性变形;当b=∞时,材料相当于完全塑性材料。
在受拉情况下,
其中:x=εt/εtr,εtr为混凝土峰值拉应变;y=σt/σtr;σtr为混凝土峰值拉应力;ft为混凝土抗拉强度。
此前,挡土墙冻胀数值模拟研究所采用的挡土墙本构多为过镇海[23]提出的模型,这会导致在模拟挡土墙受到冻胀时所发生的破坏与实际情况存在偏差,因此,本文选用邹超英[10]提出的经过冻融循环后的混凝土本构修正模型,其表达式如下:
其中:n为混凝土冻融循环次数(本文以100次冻融循环为例);Δpn为经n次冻融循环后试件的相对动弹性模量损失率。经历100次冻融循环后的混凝土受压以及受拉CDP模型所使用的其他材料参数分别见表5及表6[10]。

表5 混凝土材料受压CDP模型参数[10]Table 5 CDP model parameters of concrete material compression[10]

表6 混凝土材料受拉CDP模型参数[10]Table 6 CDP model parameters of concrete material tension[10]
3.3 冻胀力学模型
对冻胀力的分析分为2个分析步即地应力平衡步和静力分析步。数值模型的边界条件如下:1)限制模型的左右边界的x向位移,不包括挡土墙的左右边界;2) 限制模型前后边界的z向位移,同时限制底部沿x、y、z方向的位移。
由于土体和混凝土材料的变形模量存在较大差异,因此,需要在挡土墙和土体之间设置接触面单元。挡土墙和土体底部与地基的摩擦均采用摩尔-库仑摩擦,摩擦因数取为0.7。挡土墙和土体的摩擦因数取为0.5。预应力筋采用Embeded region的方式嵌入在挡土墙和土体中,并施加10 kN的初始预应力,嵌入位置为挡土墙高度的中心位置。通过导入不同时刻的温度场ODB文件即可获得不同时刻挡土墙所受到的冻胀力的分布情况。
3.4 冻胀时刻对挡土墙冻胀效应的影响
通过将每个月末的温度场导入应力分析数据中,提取沿模型中心线竖向路径上的挡土墙水平冻胀力,可以得到不同时间挡土墙所受到的水平冻胀力沿深度的分布,如图10所示。由图10可见:挡土墙所受到的冻胀力呈现由上向下逐渐增大的趋势,且在预应力筋处水平冻胀力会发生应力集中现象。
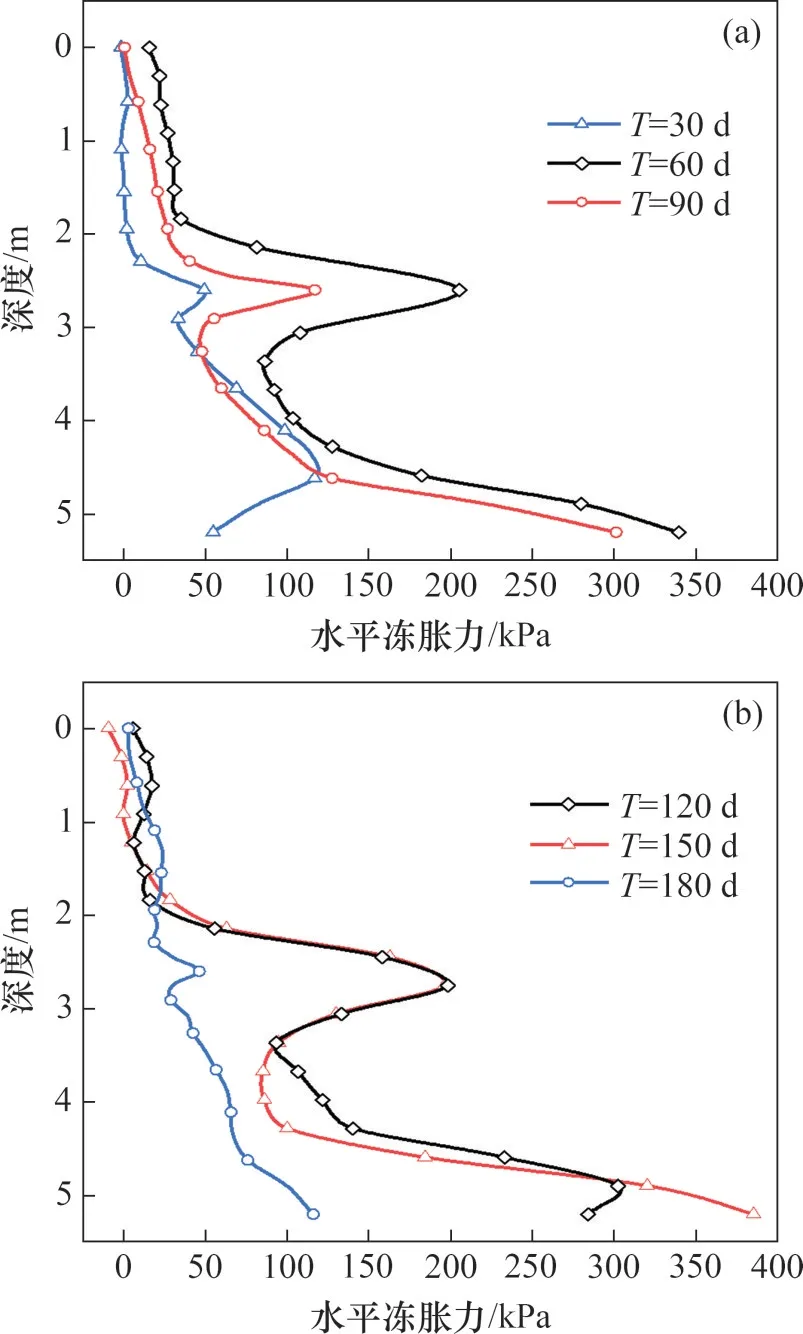
图10 不同时间挡土墙冻胀力沿深度的分布Fig.10 Distribution of frost heaving force of retaining wall along the depth in different time
分析不同冻胀时间挡土墙的水平冻胀力可以发现,自T=30 d至T=150 d,随着冻结时间的增加,挡土墙所受的水平冻胀力整体呈增大趋势。挡土墙所受冻胀力最大的时间是3月末,冻胀力达到了384 kPa。这可能是因为3月末土体的冻深最大,且土体温度主要集中在土体膨胀系数最大的临界点,导致土体内水分的膨胀变形最大,因而产生的冻胀力最大。在深度方向,挡土墙顶部2 m范围内挡土墙所受的水平冻胀力较小,最大值为40 kPa(T=60 d)。中部拉筋处的水平冻胀力由于拉筋的约束会突然增大,这与文献[24]中的试验结果较为相似;中部的冻胀力最大可达到200 kPa左右,可知预应力钢筋的存在会使挡土墙在该处产生应力集中现象;挡土墙底部的冻胀力最大,这种情况主要出现在悬臂式挡土墙的冻胀过程中[12],其主要原因是悬臂式挡土墙底部对土体的约束较强,导致挡土墙底部所受的水平冻胀力无法通过挡土墙的变形而耗散。对比挡土墙底部的冻胀力可以发现,在2008年11月末(T=30 d)以及次年2月末(T=120 d)挡土墙的冻胀力出现了较为明显的拐点,这是因为在11月末土体的冻胀深度尚未达到挡土墙最底部,此时,挡土墙底部土体的冻胀效应较小,因此,冻胀力也有明显减小;在次年2月末,挡土墙底部后方土体的冻结区域较大,土体的冻胀力可以沿背离挡土墙的方向发生小范围的流动,因此,释放了部分的冻胀力。
为了了解预应力对拉式挡墙的冻胀力变化原理,分别提取模型2009年3月末的位移云图以及节点位移图,分别如图11和图12所示。从图11可以看出,模型的位移云图呈现对称分布,挡土墙以及墙后2 m范围内土体的位移随着深度的增加而逐渐减小。模型中心梯形区域的位移较小,说明该范围土体的冻胀变形较小。从图12所示模型的节点位移可以发现,填土两侧上三角区域的土体可以自由向上方膨胀,膨胀的同时使挡土墙产生了背离土体的位移,土体在位移过程中释放了部分冻胀力,因此,挡土墙顶部2 m范围内挡土墙的冻胀力较小。随着深度的增加,挡土墙的约束能力也逐渐增强,在预应力钢筋锚固处,墙后的土体位移被约束,使冻胀力得不到释放,从而导致此处的应力集中。从模型节点位移图还可以发现,在预应力钢筋锚固处下方土体位移随着深度增大而逐渐减小,表明此处的土体受到土体自重以及挡土墙的约束作用最明显,位移相较其他区域最小,且位移方向接近水平方向,土体的冻胀不能通过变形得到释放,因此,挡土墙所受到的冻胀力随着深度增大而逐渐增大,且在挡土墙底部冻胀力达到最大。
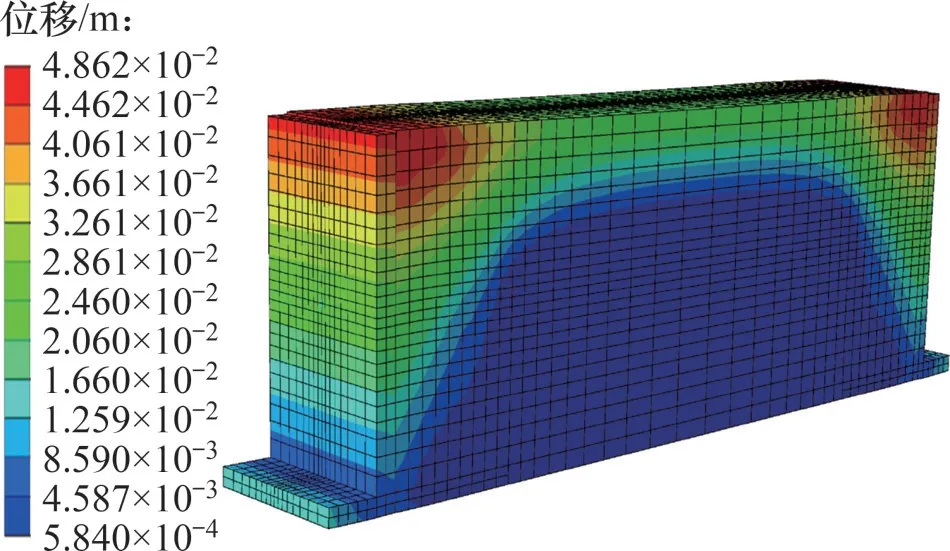
图11 模型位移云图(T=150 d)Fig.11 Displacement cloud diagram of the model(T=150 d)

图12 模型节点位移(T=150 d)Fig.12 Node displacement of the model(T=150 d)
图13所示为不同时间挡土墙的水平位移。从图13可以看出,挡土墙的水平位移呈现由上到下逐渐减小的趋势,即挡土墙顶部水平位移最大,向下逐渐减小,符合悬臂式挡土墙受到冻胀力作用时的位移变化规律。另外,预应力钢筋的存在可以较大程度地限制挡土墙的横向水平位移,导致挡土墙的水平位移曲线在预应力筋处出现了明显的转折,且冻胀力越大,这种现象越明显。挡土墙的顶部最大位移出现的时间为T=120 d,并不是挡土墙所受冻胀力最大的时间,此时的挡土墙顶部水平位移达到了8 cm。这是由于冻胀力最大时,土体表面已经开始融化,从而导致挡土墙的位移出现了一定的回位。
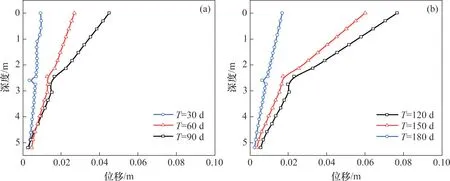
图13 不同时间挡土墙的水平位移Fig.13 Horizontal displacement of retaining wall in different time
3.5 预应力筋对挡土墙冻胀效应的影响
为了分析预应力钢筋对挡土墙所受冻胀力的影响,本文选取4个挡土墙所受冻胀力较大的月份进行分析。在同等条件下,未布设预应力对拉筋的挡土墙与布设预应力钢筋的挡土墙所受的水平冻胀力的对比结果见图14。通过对比两者的冻胀力分布可以发现:2种挡土墙所受到的土体水平冻胀力的整体分布趋势均为“上小下大”的三角形分布。二者不同之处在于:在任意冻胀时刻,预应力筋的存在会使挡土墙所受的冻胀力在该处产生应力集中现象,相较于没有预应力筋的情况,冻胀力会增大100~200 kPa,所受水平冻胀力增大86.2%~300.0%。从图14还可以发现:不同月份的应力集中程度有所不同,挡土墙底部在12月末的应力集中现象最明显,结合前述冻胀区域的划分可以得知,在12月末时土体的冻结深度还未超过预应力钢筋锚固深度,此时挡土墙后土体的冻胀一方面会受到左侧挡土墙的约束,另一方面会受到右侧未冻胀土体的限制,从而导致此时的应力集中现象较严重。而当冻结深度超过预应力钢筋锚固深度时,土体的冻胀可以向右侧移动,从而减少了预应力钢筋处的应力集中现象。
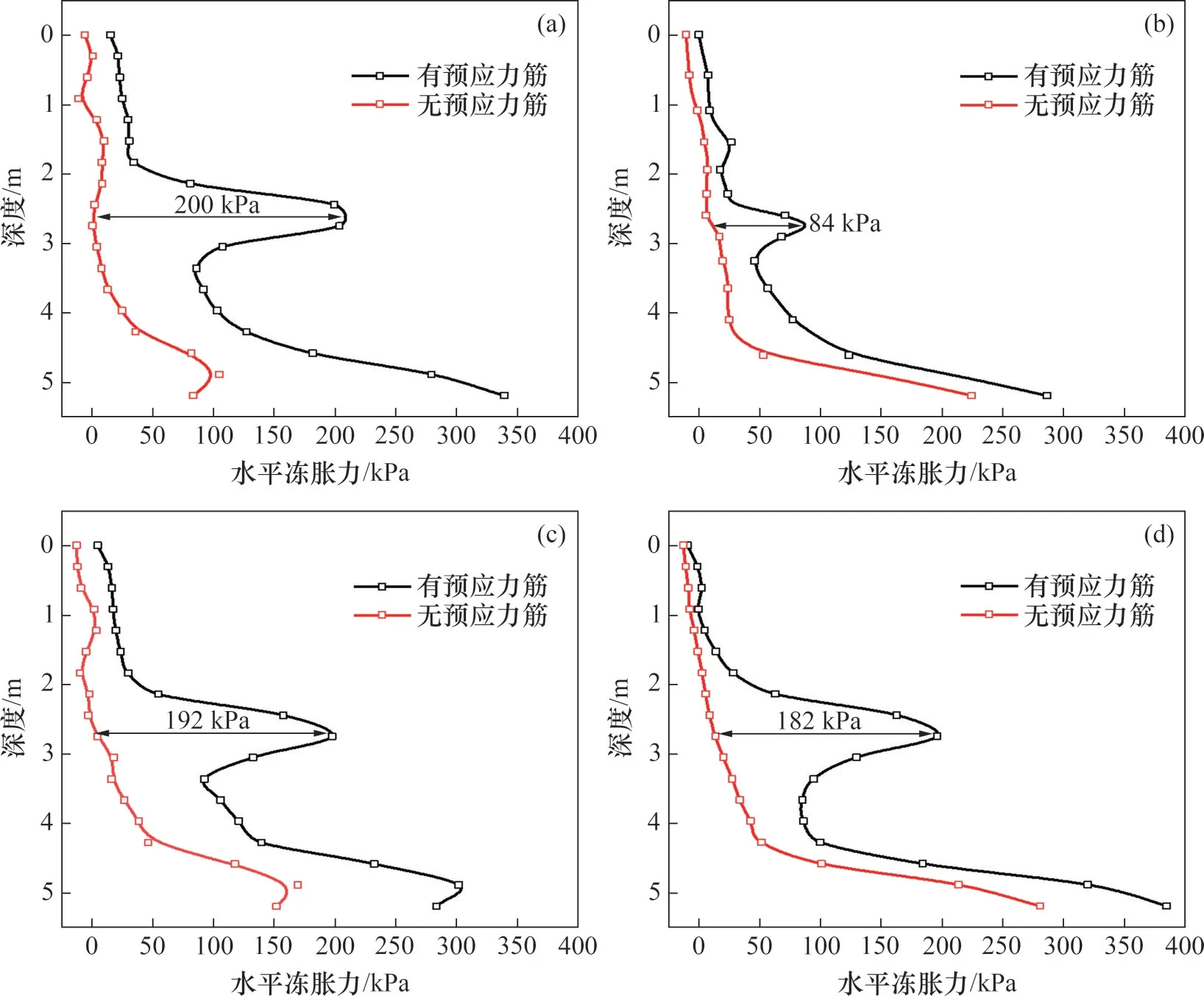
图14 不同形式预应力筋挡土墙水平冻胀力Fig.14 Horizontal frost heaving force of different forms of prestressed reinforcement retaining walls
图15所示为不同形式预应力筋挡土墙在不同时间的水平位移。通过对比同一时间含有预应力筋和不含有预应力筋的挡土墙水平位移可以发现,含有拉筋时的挡土墙在冻胀后所产生的位移较小。不含有预应力筋的挡土墙的顶部位移在2009年2月末(T=120 d)而非在冻胀力最大的2009年3月末达到最大值13 cm。这是因为在2009年3月底,随着顶部土壤的融化,挡土墙出现了一定的回位,相比之下,含有对拉式预应力筋的挡土墙位移可以使挡土墙的冻胀位移减小40%~116%,说明预应力对拉钢筋可以在很大程度上限制挡土墙的位移。
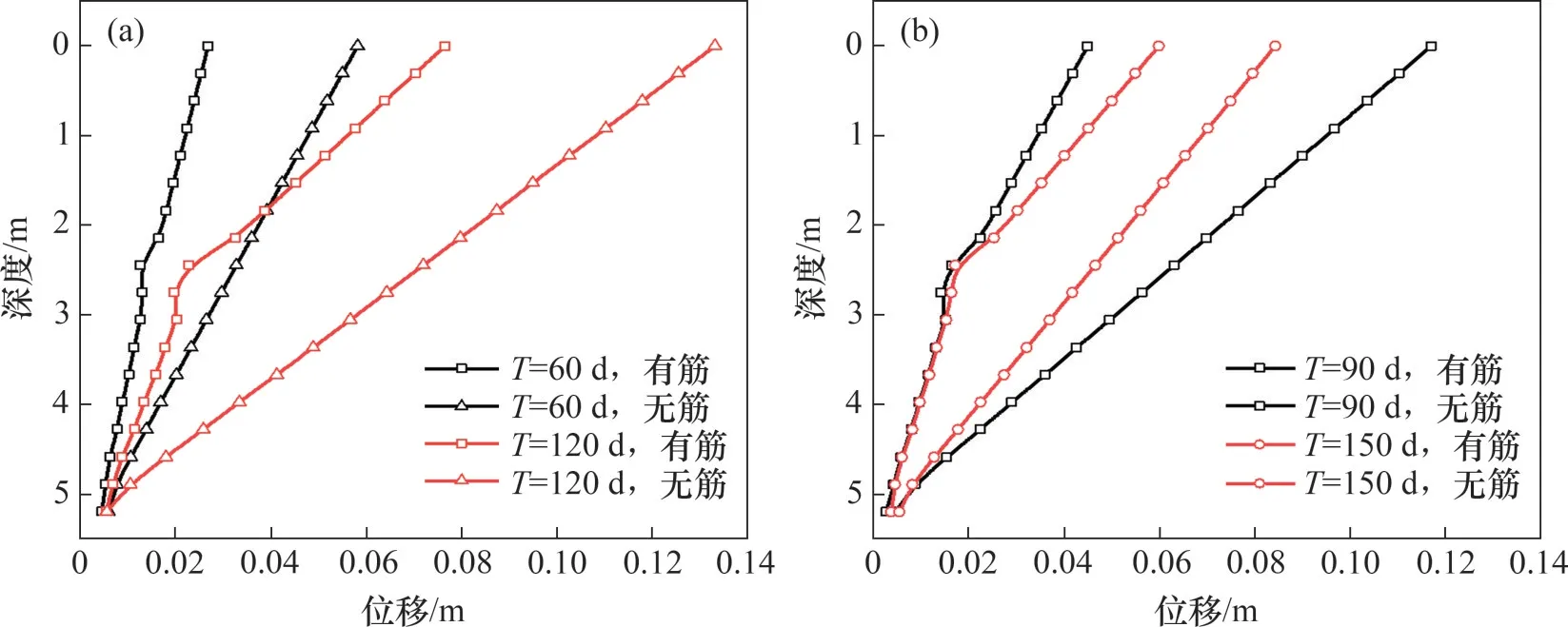
图15 不同形式预应力筋挡土墙水平位移Fig.15 Horizontal displacement of different forms of prestressed reinforced retaining walls
4 结论
1) 预应力对拉式挡土墙的模型温度场分布呈现对称分布,挡土墙后填土的最大冻结深度在3月末达到1.8 m,且地下温度场的变化主要集中在6 m深度以内。
2) 预应力对拉式挡土墙其后填土在不同冻胀时刻的冻结区分布基本呈现出3种类型,即仅挡土墙顶部后方土体冻结、挡土墙后方小范围土体冻结、挡土墙后方土体及挡土墙底部土体冻结。在不同分布情况下,挡土墙的冻胀力来源有所不同。
3) 预应力对拉式挡墙所受的水平冻胀力呈现“上小下大”的上三角分布趋势,且在预应力筋锚固处会出现应力集中现象,相比不含钢筋的悬臂式挡土墙,预应力筋处水平冻胀力增大100~200 kPa,底部水平冻胀力增大86.2%~300.0%。
4) 随着冻胀时间的增加,挡土墙墙背冻胀力先逐渐增大,然后逐渐减小。挡土墙底部冻胀力在3月底达到最大值384 kPa,预应力集中程度则是在12月末达到最大。
5) 与普通悬臂式挡土墙相比,预应力对拉式挡土墙由于预应力筋的存在,可以使挡土墙的水平位移减小40%~116%。

