边界层高度的不同诊断方法在京津冀及周边地区的适用性分析

程楠 黄鹤 张文煜 张昕宇

1 郑州大学计算机与人工智能学院/地球科学与技术学院，郑州 450001

2 天津市气候中心，天津 300074

1 引言

大气边界层，又称行星边界层，是指受地球表面摩擦、热过程以及蒸发显著影响的大气层，是大气系统的重要组成部分，其高度约为1～2 km，响应时间尺度小于1 h（Stull,1988）。大气边界层的大气运动具有明显的湍流性质，湍流过程对热量、动量和水汽的垂直输送导致气象要素呈现显著的日变化，对天气、气候和水循环有着重要的影响（刘绕等,2017;车军辉等,2021）。大气边界层是人类生产和活动的主要场所，人类活动引起的生态失衡、环境恶化以及气候变化和天气、气候异常等无一不是与大气边界层中发生的物理、化学和生态等过程密切相关（胡非等,2003）。边界层高度作为表征大气边界层特性的重要参数，反映了边界层内湍流混合、垂直扰动，对流发展等物理过程，影响热量、水汽、气溶胶等物质与能量的分布（张振州等,2013;Dai et al.,2014;张宏昇等,2020），在污染扩散、天气预报、气象模型和空气质量等研究中具有重要意义。

边界层高度的确定方法主要分为两类：观测和数值模拟。前者是基于地面观测的气象数据，结合经验公式计算边界层高度（程水源和席德立,1997），或是利用直接/遥感探测获得的温、湿、风等气象要素的垂直分布进行边界层高度的推算（Holzworth,1964;Dong et al.,2017;师宇等,2019），气块法（Holzworth,1964;Seibert et al.,2000）、位温梯度法（Stull,1988;Liu and Liang,2010）、逆温法（Bradley et al.,1993）是其常用的计算方法，后者则是根据模式模拟的结果通过不同的诊断方法计算边界层高度，湍流动能法和理查森数法是模式中常用的诊断方法（刘绕等,2017;项衍等,2019）。国内外针对不同边界层高度诊断方法的对比分析和效果评估已开展一些研究。Seidel et al.（2010）基于1999～2008 年全球505 个探空站的大气温度、位温、虚位温、相对湿度、比湿和折射率垂直廓线资料，比对分析了3 类传统方法：气块法、位温梯度法和3 类附加方法：比湿梯度法（Ao et al.,2008）、相对湿度梯度法（Kursinski et al.,1997）、折射率梯度法（Sokolovskiy et al.,2006;Basha and Venkat Ratnam,2009）等6 种方法计算的边界层高度及不确定性，发现不同方法计算的边界层高度存在几百米的差异，其中相对湿度法和位温梯度法计算的边界层高度始终较高,气块法计算的边界层高度明显偏低，相比于气块法（混合层高度）和逆温法，基于位温、相对湿度、比湿、折射率等物理量垂直梯度（最大/最小）诊断得到的边界层高度更加一致。von Engeln et al.（2013）利用欧洲中心长序列再分析数据ERA-Interim 的大气温度、压强、位势高度、相对湿度等数据对比分析了相对湿度梯度法、比湿梯度法、位温梯度法、虚温梯度法和折射率梯度等计算的边界层高度的差异，结果表明基于相对湿度梯度法计算的边界层高度，其平均值和标准差与基于探空数据的计算结果基本一致，进一步的分析发现陆地上的边界层高度表现出较大的季节变化和日变化。刘超等（2017）利用北京市南郊观象台（站号54511）的L 波段探空雷达秒级数据和地面常规观测资料MICAPS 数据对比分析了总理查森数法、逆温法、位温梯度法和罗氏法计算的边界层高度，研究发现在典型的晴空或云量较少的静稳天气中，各方法计算结果相近，当出现弱降水和大气污染混合等复杂天气时，不同算结果相差较大。任桂萍等（2020）使用甘肃酒泉的探空雷达数据比较了干绝热曲线法、理查森数法和位温梯度法，研究表明干绝热曲线法计算的大气边界层高度更能反映酒泉大气边界层的真实情况。可见，边界层高度对诊断方法非常敏感，不同诊断方法因受地形、海陆分布、纬度等复杂下垫面以及云和降水、污染、信风等复杂天气的影响，其在同一地区的计算结果存在显著的差异，也表现出不同的时间变化特征。

京津冀及周边地区地处华北，地势西北高、东南低，东部濒临渤海、海陆分布明显，南北纬度差异较大，区域内有山地和平原等多种复杂地形，同时拥有三大世界级城市群—京津冀城市群。京津冀协同发展是中国当前三大国家战略之一，科学的诊断京津冀及周边地区的大气边界层高度，有助于研究该地区大气边界层结构，加深对复杂地理条件下边界层时空演变特征的理解，同时为区域性污染天气形成机制研究、大气环境容量评估以及污染气象条件、空气质量和低能见度天气预报等研究提供重要参数支撑。本文基于京津冀及周边地区7 个国家级气象台站的探空数据，采用基于热力作用的传统的位温梯度法和改进的位温梯度法（Liu and Liang,2010）、基于水汽分布的相对湿度梯度法和比湿梯度法、以及动力和热力相结合的理查森数法等5 种诊断方法，计算各站2016～2021 年的大气边界层高度，对比分析不同方法计算的边界层高度，从时间变化和地理位置的角度探讨各诊断方法的差异性。

2 资料与方法

2.1 资料

本文使用的数据是“天擎气象大数据云平台”全国高空定时值资料中北京（54511）、张家口（54401）、邢台（53798）、赤峰（54218）、乐亭（54539）、章丘（54727）、太原（53772）7个探空站2016～2021 年（站点分布见图1）每天早上08:00（北京时间，下同）和晚上20:00 的探空数据，包括位势高度、气温、露点、气压、风向、风速等要素。因为研究的是边界层高度，所以只取离地高度4 km 以下的探空数据，对探测层数小于8 层的进行剔除，各站点有效的样本数如表1 所示。

表1 站点样本数统计Table 1 Sample number statistics of stations

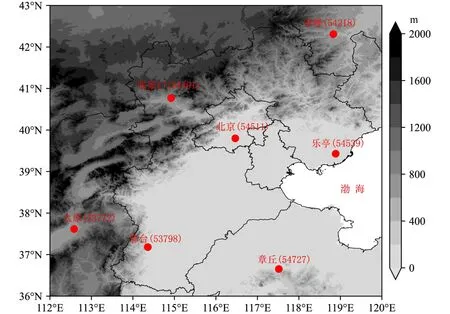
图1 京津冀及周边地区7 个探空站点分布（阴影表示海拔高度）Fig.1 Distribution of sounding stations (shadow represents altitude)

2.2 边界层高度诊断方法

从影响大气边界层高度的热力、动力、物质分布角度出发，选取典型的边界层高度诊断方法：考虑热力作用的位温梯度法，考虑物质分布的相对湿度梯度法和比湿梯度法，综合考虑动力和热力作用的理查森数法。

2.2.1 位温梯度法

（1）传统的位温梯度法（G_θT）

由于边界层内温度、水汽分布相对均匀，位温梯度变化较小，而在边界层高度以上位温梯度迅速变大，因此将位温梯度最大处的高度取作大气边界层高度（Stull,1988;刘超等,2017）。计算公式如下：

其中，z是观测高度，单位：m；T是高度z上的气温，单位：K；θ是高度z上的位温，单位：K；p是高度z上的压强，单位：hPa；是位温梯度，单位：K/m。

（2）改进的位温梯度法（G_θLL）

该方法在传统的位温梯度法的基础上，通过大气层结状态将边界层细分为稳定边界层（SBL）、中性边界层（NBL）和对流边界层（CBL）三类，通过计算200 m 和50 m 之间的位温差来区分边界层类型（Liu and Liang,2010）：

其 中，θ200表示200 m 处位温，θ50表 示50 m处位温，δs=1 K。CBL 和NBL 情况下：当第k个高度层的位温 θk满足 θk-θ1≥δu时，k高度层以上第一个满足式（3）的高度即为边界层高度。

SBL 情况下：当第k层和第k－1 层的位温梯度满足式（4）时，第k层的高度即为边界层高度。

其 中，δu=0.5 K，

2.2.2 相对湿度梯度法（G_RH）

在大气边界层内，水汽分布密集，具有较大的垂直湿度梯度，边界层顶部上方相对湿度变化较大，可将相对湿度变化最明显（梯度最小）的高度作为大气边界层高度（Kursinski et al.,1997;Seidel et al.,2010）。计算公式如下：其中，Uw是对应高度z的相对湿度（单位：%）；Es是饱和水汽压（单位：kPa），温度T≥0时，a=7.5，b=237.3，T＜0 时，a=17.67，b=243.5；Ea是实际水汽压（单位：kPa）；是相对湿度梯度 。

2.2.3 比湿梯度法（G_q）

从大气边界层到自由对流层的过渡通常以温度和水汽的显著变化为标志，水汽剖面的量（例如比湿或水汽压）会在穿过大气边界层顶时而减小，因此可以将比湿梯度最小的位置作为大气边界层高度（Ao et al.,2012）。计算公式如下:

其中，q是对应高度z的比湿（单位：g/kg）；ε=Mv/Md=0.622，式中Mv是水汽的摩尔质量，Md是干空气的摩尔质量；Uw是相对湿度；Es是饱和水汽压；q˙是 比湿梯度。

2.2.4 理查森数法（Ri）

参照Sicard 提出的理查森数法计算公式（Sicard et al.,2006）：

其中，g是重力加速度，取9.81 m s-2；z0为地面海拔高度；u和v分别为纬向和经向风分量，通过对观测到的水平风速进行分解得到。将理查森数Ri达到一个临界值（0.25）时的最低高度选为大气边界层高 度（Seidel et al.,2012）。

3 结果分析

3.1 不同方法间的结构性差异

不同边界层高度诊断方法基于不同要素的垂直廓线确定边界层高度，存在较大的不确定性。图2给出了2021 年3 月28 日08:00 和2021 年6 月23日20:00 北京（54511）探空站位温（θ）、相对湿度（RH）、比湿（q）和理查森数（Ri）的垂直分布以及5 种诊断方法计算的大气边界层高度。可以看到，对于3 月28 日8:00 的大气廓线特征，各方法计算的大气边界层高度表现出极好的一致性，均为963 m（图2a），5 种方法在6 月23 日20:00 诊断的大气边界层高度相差较大（图2b），Ri 给出的边界层高度最小为386 m，G_q 和G_θLL得到的边界层高度较高，在1000 m 左右，G_θT计算的边界层高度为1833 m，G_RH 给出的边界层高度最高，达到3015 m。因此，对边界层高度不同诊断方法进行比较和评估，分析它们在京津冀及周边地区的优缺点和不确定性，对京津冀及周边地区边界层研究和业务应用是非常必要的。

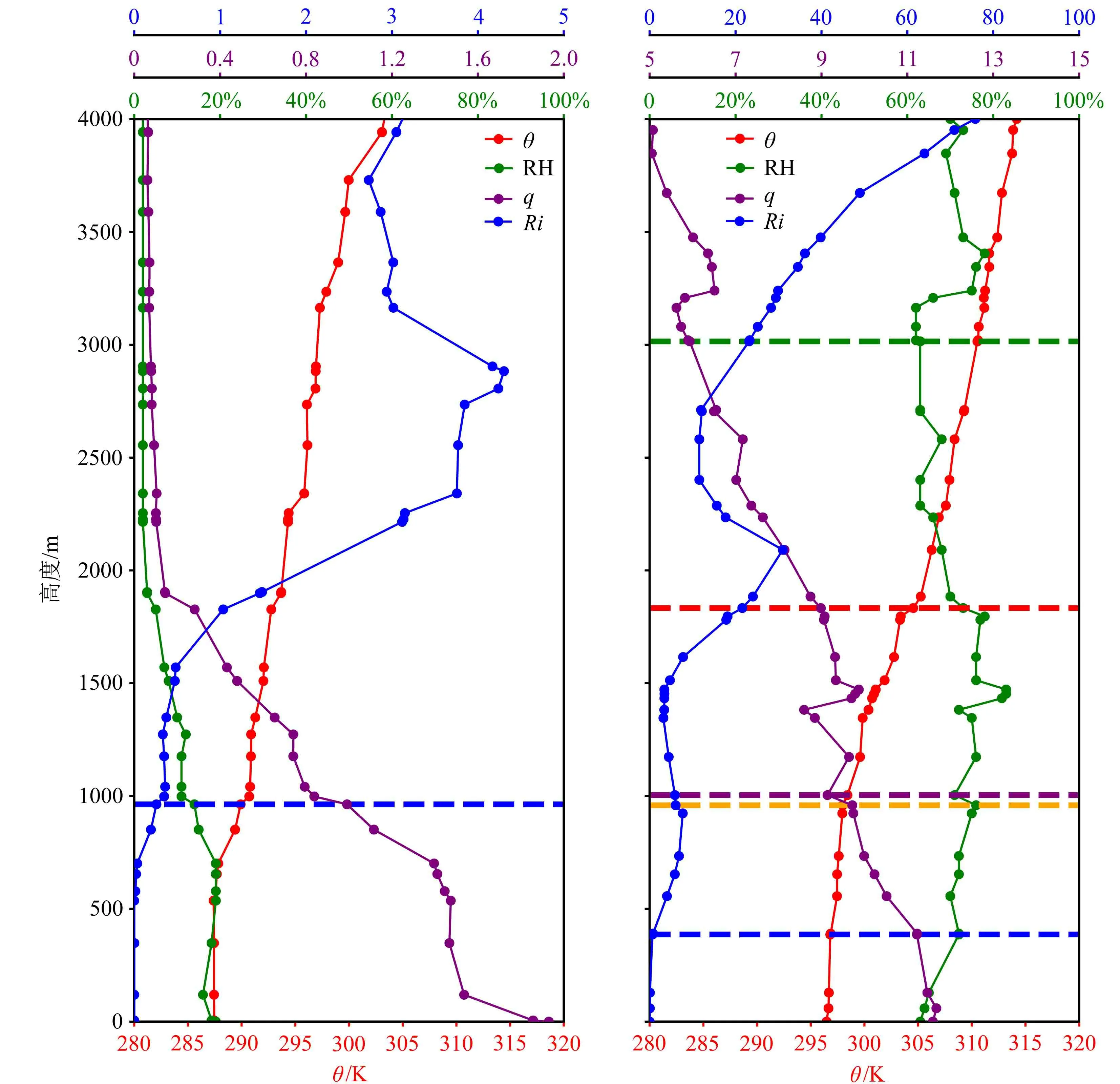
图2 基于5 种诊断方法计算的2021 年（a）3 月28 日08:00 和（b）6 月23 日20:00 北京站大气边界层高度。垂直廓线分别为位温（θ，红色）、相对湿度（RH，绿色）、比湿（q，紫色）和理查森数（Ri，蓝色）。红、黄、紫、绿、蓝5 种颜色虚线分别表示传统的位温梯度法（G_θT）、改进的位温梯度法（G_θLL）、相对湿度梯度法（G_q）、比湿梯度法（G_RH）和理查森数法（Ri）边界层高度计算结果Fig.2 The atmospheric boundary layer height of Beijing sounding station at (a) 0800 LST 28 March 2021 and (b) 2000 LST 23 June 2021 based on five diagnostic methods.The vertical profiles are potential temperature (θ,red),relative humidity (RH,green),specific humidity (q,purple),and Richardson number (Ri,blue).The dashed lines show the boundary layer height calculation results of different methods respectively.The five colors of red,yellow,purple,green,and blue respectively represent the traditional potential temperature gradient method (G_θT),improved potential temperature gradient method (G_θLL),relative humidity gradient method (G_q),specific humidity gradient method (G_RH),and Richardson number method (Ri)

图3 给出了7 个探空站基于不同诊断方法得到的08:00 和20:00 两个时刻的年大气边界层高度均值和中位值的多年平均。总体上来看，各种方法诊断的大气边界层高度的平均值均在1534 m 以下，中位值在429～1453 m，20:00 高于08:00。所有方法中，G_RH 计算边界层高度最大，08:00 为1241 m，20:00 为1534 m；Ri 计算结果最小，08:00 和20:00 分别为473 m 和562 m，另外3 种方法计算结果集中分布在846～1118 m（08:00）和981～1298 m（20:00）。从边界层高度均值和中位值差距可以看到，Ri 计算的边界层高度的均值与中位值最为接近，二者相差仅为45 m（08:00）和7 m（20:00），说明Ri 计算结果分布集中，离散程度低。相比之下，G_θT计算结果中位值和平均值之差达到543 m（08:00）和345 m（20:00），G_θLL计算的边界层高度与G_θT相比，平均值分别降低137 m（08:00）和317 m（20:00），中位值更加接近平均值。对比G_RH 和G_q 两种湿度法在不同时段的结果可以看到，08:00 两种方法计算结果的中值和均值差异更大，20:00 两种方法计算的边界层高度的中值和均值差异更小。

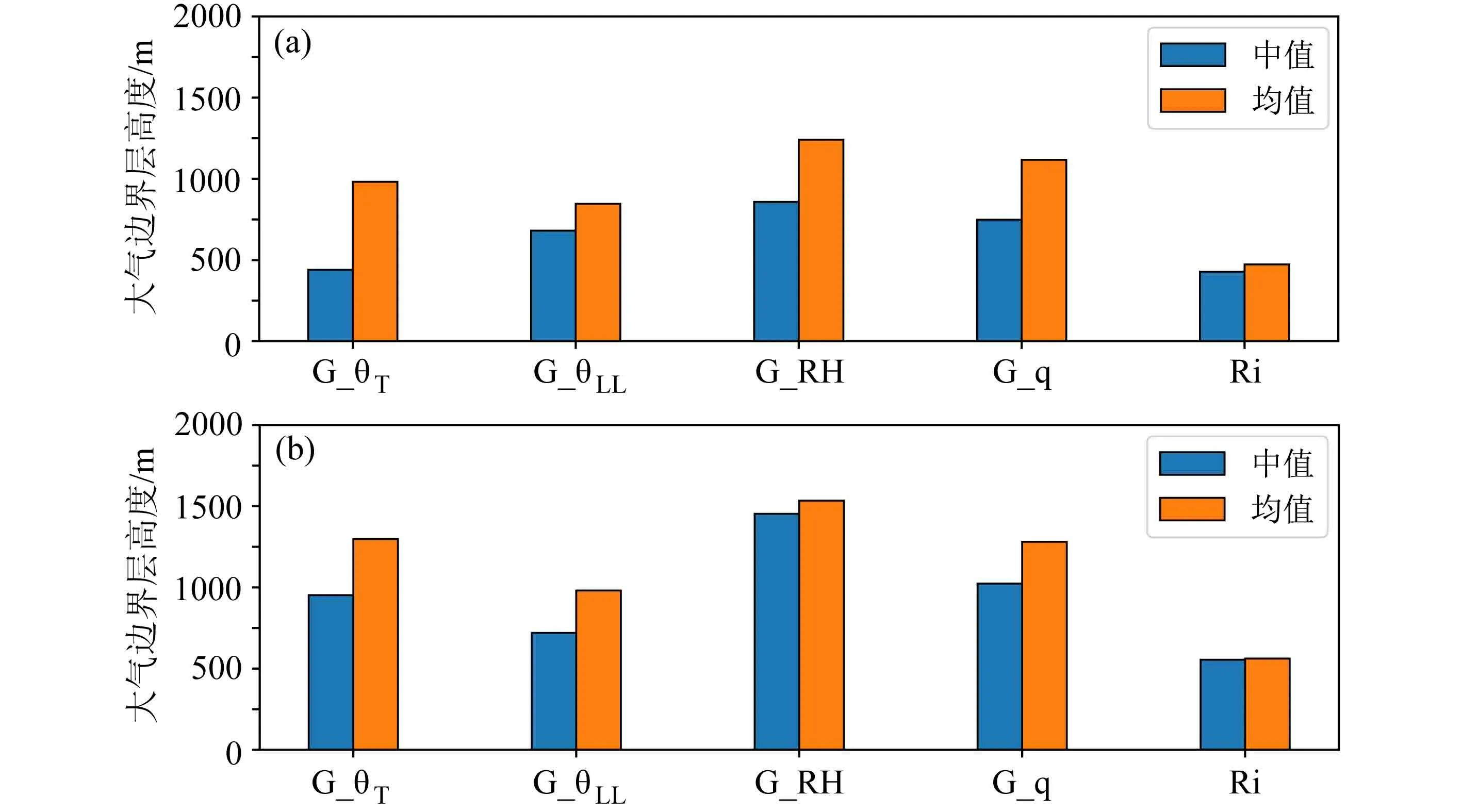
图3 利用5 种方法计算的所有探空站（a）08:00 和（b）20:00 多年平均的年大气边界层高度均值和中值（2016～2021 年）Fig.3 Annual mean and median atmospheric boundary layer heights calculated at (a) 0800 LST (a) and (b) 2000 LST of all sounding stations using five methods (2016-2021)

为了进一步对比5 种方法计算的大气边界层高度差异，对5 种方法在早晚时刻的计算结果进行显著性检验（表2～5），包括T检验、F检验、K-S（Kolmogorov-Smirnov）检验、皮尔逊相关性检验。可以看到，任意两种方法计算的边界层高度均通过显著性检验（P=0.05），不同方法之间存在显著的差异。从T检验结果来看，Ri、G_θLL的检验值均为负值，说明这两种方法计算的边界层高度较G_θLL偏小，相反，两种湿度法计算的边界层高度较G_θLL偏大，与图3 所展示的结果一致。方差比F检验显示，G_θT、G_q 和G_RH 这3 种方法计算结果的离散度最为接近，离散度由低到高依次为G_q、G_θT和G_RH，相比之下，G_θLL离散度更小，Ri 的离散度最小。5 种方法之间均具有显著相关性（表3 和表5），除了两种湿度法之间的相关性较高外（r≥0.67），其他方法之间的相关系数均较小（r≤0.46），多数皮尔逊相关系数在0.3 以下，Ri 法与G_q 法之间的相关性最低，仅为0.1（08:00）和0.13（20:00）。从K-S 检验来看，Ri 计算结果的累积分布与其他4 种方法的差异最大，G_θT与G_q 的累计分布最为接近。综上分析，选择的诊断方法不同导致计算的边界层高度存在较大的结构不确定性，使用平均值差异代表结构不确定性，差异从50 m 左右到湿度法相关的1019 m。

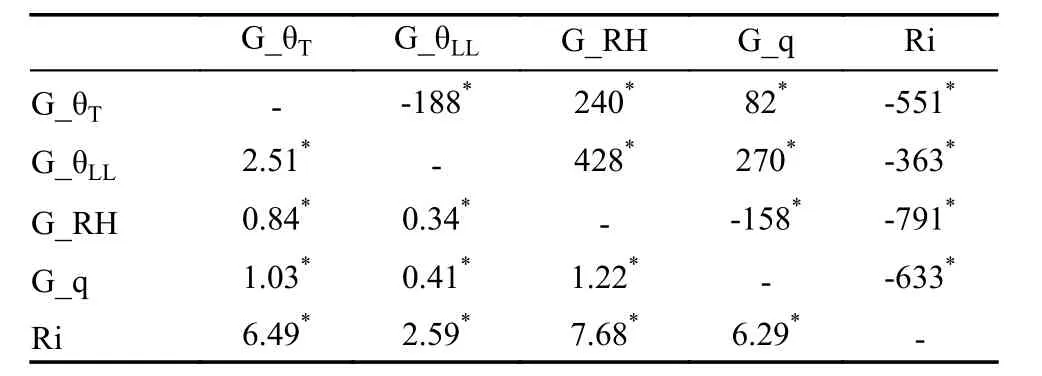
表2 5种方法计算的08:00 边界层高度差异T 检验（右上）和边界层高度方差比值F 检验（左下）结果Table 2 The T-test (upper right) and F-test (lower left)results of the boundary layer height at 0800 LST calculated using the five methods

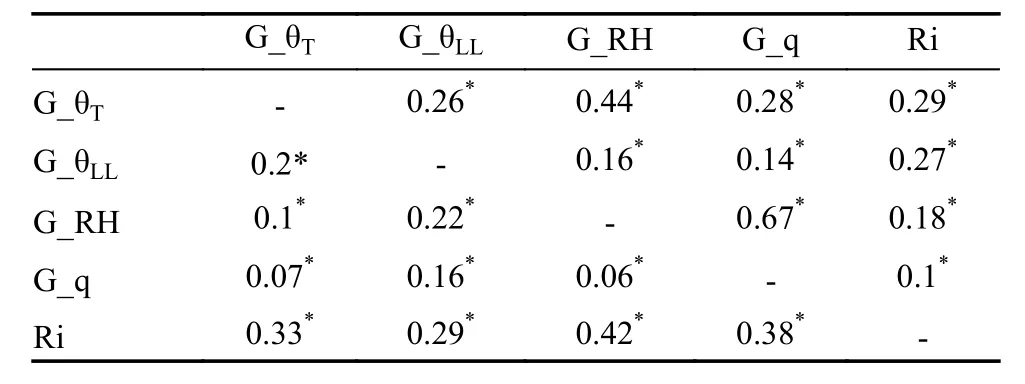
表3 5 种方法计算的08:00 边界层高度的皮尔逊相关性检验（右上）和统计量D 值K-S 检验（左下）结果Table 3 Pearson correlation test (upper right) and K-S test(lower left) results of boundary layer height at 0800 LST calculated using the five methods

表4 5 种方法计算的20:00 边界层高度差异T 检验（右上）和边界层高度方差比值F 检验（左下）结果Table 4 The T-test (upper right) and F-test (lower left)results of the boundary layer height at 2000 LST calculated using the five methods

3.2 不同方法间的季节性差异和季节内差异

边界层高度的季节变化特征往往与夜间辐射逆温、信风逆温、热对流和云量等局地气候特征密切相关，不同的下垫面类型如山地、城市、海陆交界等复杂下垫面，也常常造成其上的边界层变化不尽相同，因此不同边界层高度诊断方法在时间尺度上和不同下垫面条件下的适用性评估非常重要。根据京津冀及周边的地形地貌、海陆分布、城市群分布特点，选取临近海洋的乐亭站、内陆低海拔的北京站和高海拔的太原站（表1 和图1）做为典型站点，对比分析五种边界层高度诊断方法在3 类典型站点上月、季时间尺度上的差异，同时采用四分位距考察样本数据因所选方法带来的参数不确定性。

图4～6 给出了利用5 种诊断方法计算得到的乐亭、北京和太原3 个站点08:00 和20:00 时边界层高度的季节变化，包括第一分位数、第二分位数（中位数）、第三分位数和四分位距。可以看到，五种方法得到的3 个站点的边界层高度具有明显的季节性差异和季节内差异，两种湿度法在乐亭呈现夏秋高、春冬低的特点，在北京和太原呈现春夏高、秋冬低的特点，其他方法在3 个站都是春夏高、秋冬低的特点。

图4 2016～2021 年乐亭站大气边界层高度的季节变化（红色、橘色、绿色、青色、蓝色代表不同方法的第一份位数值，白色斜线部分为第二分位数值，灰色斜线部分为第三分位数值，斜线部分为四分位距）Fig.4 Seasonal variation of atmospheric boundary layer height in Laoting during 2016-2021 (Red,orange,green,cyan,and blue represent the first digit values of different methods.The white slash is the second digit value,the gray slash is the third digit value,and the slash is the interquartile distance)

图5 同图4，但为北京站Fig.5 Same as Fig.4,but for Beijing station

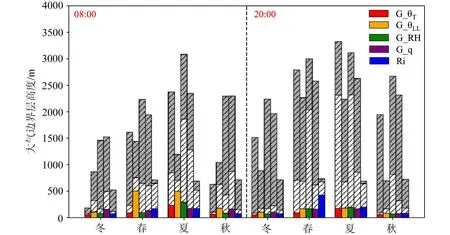
图6 同图4，但为太原站Fig.6 Same as Fig.4,but for Taiyuan station

对于乐亭站，冬季早上G_θLL得到的边界层高度（第二分位数值）明显高于其他4 种方法，晚上G_θT的计算结果更高；春季，早晚两个时刻各方法之间的差异基本一致，均是G_θLL和Ri 得到数值相当的较大边界层高度，G_θT和G_RH 的结果相对较小，G_q 最小；夏秋季，G_RH 计算得到的边界层高度在早晚时刻总是最大，除秋季早上G_θLL和G_q 的计算结果与G_RH 相当外，其他时间另外4 种方法得到的结果均较G_RH 明显要小。对比各种方法各季节的四分位距来看，单个方法早晚两个时刻的计算结果一致性较好，但不同方法间的参数不确定性存在明显的季节性差异。从图4 中可以看到，在所有的诊断方法中，Ri的计算结果在各季节两个时刻的四分位距最小在210～613 m，说明该方法得到的边界层高度离散度更小，即参数不确定性更小。相比之下，冬季G_θT的四分位距最大，最大值达到1298 m（08:00）和1794 m（20:00），G_RH 次之，其他春、夏、秋3 个季节G_RH 的四分位距最大，最大值分别为1341 m、2246 m、1681 m（08:00）和1856 m、2243 m、1967 m（20:00），G_θT次 之，可见G_RH 和G_θT各个季节的参数不确定性更大。对比G_θT和G_θLL两种位温梯度法可以看到，后者得到的边界层高度及其参数不确定性更小，此种情况同样出现在G_RH 和G_q 两种湿度法的计算结果中。

对于北京站，对比各个季节中各方法得到的边界层高度可以看到，秋、冬两季各方法之间的差异性相类似，均是早上G_θT和Ri 得到较小边界层高度，其他3 种方法得到较大的、数值相当的边界层高度，晚上是G_RH 的结果最大，G_θT、G_θLL和G_q 相对较小，Ri 最小。相比之下，春、夏两季各方法之间的差异性特征更加接近，早上G_θT、G_θLL和G_RH 得到的边界层高度相对较大，G_q和Ri 相对较小，而晚上则是G_θT、G_RH 和G_q 3 种方法得到的结果相对较大，另外两种方法的结果较小。从各方法的参数不确定性来看，Ri 计算的边界层高度最小，G_RH 的结果最大，G_θT次之。各方法在太原站的总体表现与北京站一致，但仍存在一些差异，如秋、冬季早上G_RH 得到比其他方法更低的边界层高度，G_θT的参数不确定性比Ri 的更小。

综合以上分析可以看到，由于乐亭、北京、太原3 个站属于同一气候带，边界层高度的季节变化总体上保持一致，均具有北半球中纬度地区大陆性边界层的特征。下垫面的不同使得各诊断方法在各站点的计算结果不尽相同，北京站和太原站作为内陆城市站，在海拔高度上存在差异，但单一方法的季节性差异特征比较一致，各方法之间的季节内差异（冬季除外）也较为类似。相比之下，位于沿海地区的乐亭站，受到海洋的影响，单一方法的季节性差异和各方法间的季节内差异均与北京和太原两站有所不同。从参数不确定性来看，两种湿度法的参数不确定性大，各站点边界层高度的四分位距普遍较大。Ri 的参数不确定性最小，除太原站秋冬季Ri 计算的边界层高度四分位距在早上8 时比G_θT的结果略大外，其他时期Ri 计算结果的四分位距均是所有方法中最小的。

3.3 时间一致性分析

为进一步评估各方法计算结果的时间一致性，图7～9 分别给出了乐亭、北京和太原3 个站点上5 种方法计算的2016～2021 年边界层高度的月变化和任意两种方法计算结果的皮尔逊相关系数，相关系数黑色数值代表通过95%的显著性检验，红色值表示未通过。从图7 中可以看到，5 种方法得到的乐亭站边界层高度月变化一致性总体较差，各方法之间的相关性总体呈现晚上高、早上低的特征。两种湿度法得到的边界层高度月变化一致性较好，二者相关系数可达到0.93（08:00）和0.96（20:00），均通过显著性检验。两种湿度法与其他3 种方法间的相关性差异较大，与G_θT间的相关性相对较好，早晚相关系数均能达到0.69 以上，与G_θLL和Ri间的相关性相对较差，早上更为明显，相关系数均不足0.5，且未通过显著性检验。对比G_θT、G_θLL和Ri 之间的相关性可以发现，G_θLL与Ri 的变化趋势较为接近，相关系数可达到0.91（08:00）和0.84（20:00），与G_θT的相关性不明显，早晚时刻的结果均未通过显著性检验，G_θT与Ri 的相关性在早上较好，夜间较差。

相对于乐亭站，各方法计算的北京边界层高度月变化的一致性有所提升，呈现出晚上高、早上低的总体特征（图8），但各方法在两个站点的表现仍有所不同，如北京站G_q 与G_θT间的相关性较乐亭站明显较差，而G_θT与G_θLL间反而呈现出非常高的一致性，相关系数分别达到0.79（08:00）和0.96（20:00），且通过了显著性检验。此外，G_θT和Ri 在晚上呈现出较高的相关性（r=0.83）。从太原站各种方法相关性热力图可以看到（图9），太原站不同方法间的一致性情况与乐亭和北京站相似，相关系数更高，最小的相关系数也达到了0.61（G_q 和G_θLL，08:00），均通过显著性检验。

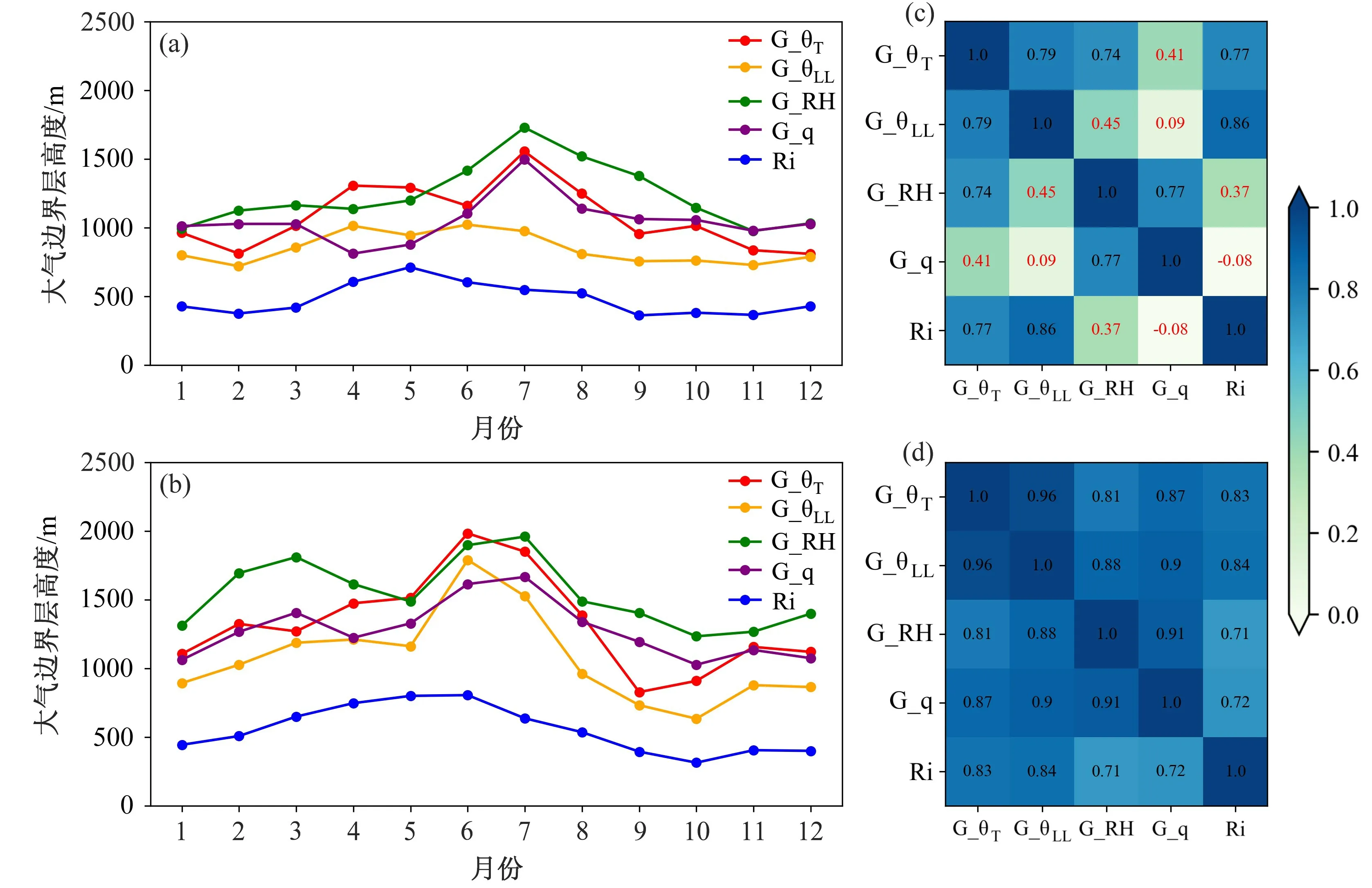
图8 同图7，但为北京站Fig.8 Same as Fig.7,but for Beijing station

通过以上分析可以看到，在3 个代表站边界层高度月变化的一致性上，各种方法均呈现出晚上高、早上低的特点，方法间的相关性也表现出较为一致的特征，仅在相关程度和个别方法间相关性（G_q与G_θT、G_θT与G_θLL）上存在差异。两种湿度法以及G_θLL与 Ri在3 个代表站均具有稳定的相关性，而G_θT与其他方法间的一致性在不同站点的波动较大。

4 结论

基于2016～2021 年京津冀及周边地区7 个探空站数据，对比分析了传统的位温梯度法、改进的位温梯度法、相对湿度梯度法、比湿梯度法和理查森数法5 种大气边界层高度诊断方法的结构性差异以及在不同代表站上的季节性差异和时间一致性。主要结论如下：

（1）5 种方法诊断的大气边界层高度存在显著差异。各方法计算的边界层高度的平均差异在40～1000 m，其中，两种湿度法和位温梯度法3 种方法的计算结果偏高，改进的位温梯度法偏低，理查森数法最低。两种湿度方法计算的结果显著相关（相关系数在0.6 以上），传统的位温梯度法、改进的位温梯度法和理查森数法之间显著相关（相关系数在0.29～0.5），两种湿度法与其他方法之间的相关性不高。不同方法诊断的边界层高度存在较大的结构不确定性，普遍差异可达到数百米，基于梯度的方法往往给出较高的边界层高度，考虑更多背景条件的理查森数法和改进的位温梯度法得到较低的边界层高度。

（2）下垫面不同导致各方法间存在一定季节性和季节内差异。两种湿度法在乐亭呈现夏秋高、春冬低的特点，在北京和太原呈现春夏高、秋冬低的特点，其他3 种方法在3 个站均是春夏高、秋冬低的特点。北京、太原两个内陆城市站的单一方法季节性差异和各方法间的季节内差异特征（冬季除外）均比较相似，受海洋影响较大的乐亭站则有所不同。在参数不确定性方面，两种湿度法最大，理查森数法最小。

（3）各方法在不同站点边界层高度时间一致性上呈现出较为类似的特征。各方法间的相关性均表现出晚上高、早上低的特征，仅在相关程度和个别方法间相关性上存在差异。两种湿度法以及改进的位温梯度法与理查森数法之间的相关性较为稳定，而传统的位温梯度法与其他方法间的一致性因站点不同波动较大。

（4）整体来看，理查森数法诊断的边界层高度更稳定，参数不确定性最小，诊断结果的时间变化符合实际情况，适用于京津冀及周边地区边界层高度的诊断。