基于REOF分析的山东省年降水区域特征及趋势分析

任建成, 谷山青, 卢晓宁

(1.山东省气象防灾减灾重点实验室, 济南 250031; 2.滨州市气象局, 山东 滨州 256612; 3.成都信息工程大学, 成都 610225)

气候变化已成为科学界的共识。IPCC第五次评估报告[1]指出,近百年来温室气体浓度的增加导致了全球大气和海洋变暖是毋庸置疑的。IPCC第六次评估报告[2]进一步指出,气候变化加快了水循环,并对降水特征产生明显影响。《中国气候变化蓝皮书(2022)》[3]指出:全球变暖趋势仍在持续,2012年以来中国年降水量持续偏多,中国平均年降水量总体呈较明显增加趋势,且不同区域间降水特征差异明显,全球范围内的极端降水事件频发。全球变暖背景下各地降水变化的研究也早已成为了国内外的研究热点[4-6]。

目前,全球范围内对于降水研究主要集中于降水变化特征及地域性差异、季风区和非季风区降水特征对比、极端降水变化等方面。如Donat等[7]的分析认为全球干旱区降水明显增加,且受温度升高的影响比较明显,但湿润区降水量变化并不显著。Wang等[8]的研究表明季风降水不仅与太阳辐射能量有关,跟地球内部的反馈机制也密切相关,南方涛动增强了全球季风降水,热带和亚热带地区极端降水强度增加速度大大高于全球,但是在其他地区模拟的物理机制尚存在不确定性。

国内对于降水变化特征及影响机制、极端降水也进行了大量的研究。过去几十年,国内降水量整体变化不显著[9],但东南沿海、长江下游、青藏高原和西北地区年降水量呈增加趋势,东北、华北和西南地区降水量呈减少趋势,特别是东北地区和华北地区年降水量呈显著减少趋势,尤其是夏季降水[10-12]。近年来及未来一段时间,我国极端降水普遍呈增多趋强趋势,其中极端降水事件增幅最大的地区为华北和东北[13]。

山东省是中国华东地区的一个沿海省份,气候属暖温带季风气候类型,境内存在山地、丘陵、平原、盆地等多种地貌。对于山东省降水特征的研究,有徐泽华等[14]研究认为,1981—2010年期间,山东省年降水量呈现上升趋势,降水的振荡周期与南方涛动和东亚夏季风存在一定的响应关系。卢仲翰等[15]的研究则表明1961—2017年期间,山东省降水量年降水量呈不显著减少趋势,降水的空间高值中心出现在泰山山脉的周边。刘玄[16]的研究表明:山东省多个极端降水指数呈显著上升趋势,且地域差别较大。上述研究均从整体上分析了山东省的降水特征。地形、海陆位置等因素会对地区气候产生比较明显的影响[17-18],鉴于山东省海陆并存、地貌复杂的地理特点,仅从整体上对山东省降水进行研究,不能很好地体现山东省降水的区域特征。因此,本文首先对山东省年降水场进行气候分区,并对各区域的年降水时空分布特征进行更加深入的研究,为山东省气候分析、防灾减灾提供更加区域性的参考依据。

1 研究资料和方法

1.1 研究资料

根据世界气象组织的建议,到2021年应使用1991—2020年的新气候基准线,而高质量气候值是应对气候变化亟需的重要科学数据之一。得益于中国地面自动观测系统的发展及观测数据完整性和质量的提升,本文研究资料采用中国气象局研制的1991—2020年中国地面气候数据集,该数据集基于国家气象信息中心归档的中国地面观测数据,对1991年以来的地面台站观测数据集元数据进行了系统的质量检查和核实订正。在基于站址迁移信息对所有要素进行了分段处理基础上,采用傅里叶级数理论对气温、降水等累年日值序列进行了谐波处理,在体现气象变量季节性转换的同时,避免了日与日之间的异常突变特征,具有更好的气候代表性。最终建立的1991—2020年中国地面气候值数据集提供了中国2 438个站点的气候背景信息,为天气气候业务提供了数据支撑。本文选用山东省95个气象站点1991—2020年降水年值数据进行分析研究,选用的站点全部为山东省气象局当前业务观测站点,降水数据可以较好地体现山东省年降水变化特征,站点空间分布详见图1,各气象站点年平均降水量(mm)描述统计特征见表1。

表1 山东省各气象站点年平均降水量描述统计特征

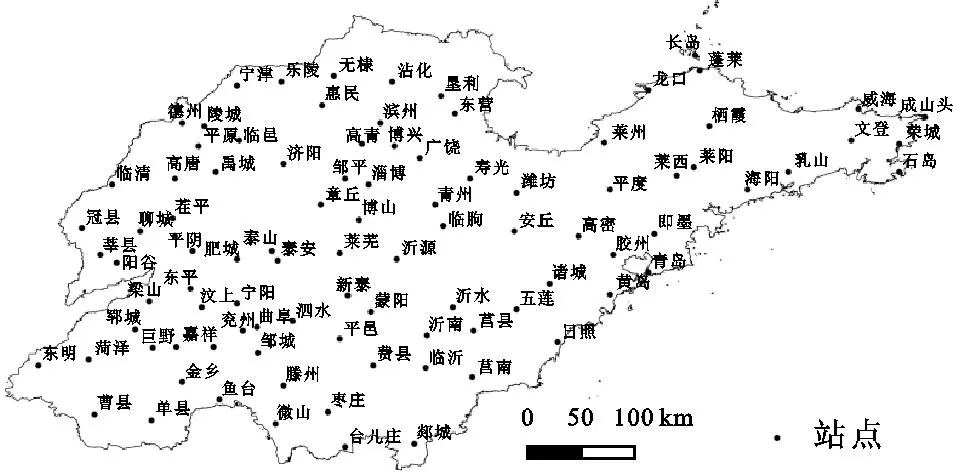
图1 山东省气象站点分布

1.2 研究方法

1.2.1 EOF及REOF方法 经验正交函数(Empirical Orthogonal Function,简称EOF)通过North显著性检验,把时间序列中集中到少数几个显著的时空模态上,已在气候等领域应用较多[19-21]。主要计算过程分为3步:

首先标准化处理原始数据矩阵,求得标准化矩阵X。

然后通过矩阵X及其转置矩阵XT,得到相关系数矩阵A。

最后求矩阵A的特征值λ、特征向量V和时间系数Z,并计算可以通过North显著性检验的前P个特征向量的方差贡献率。

North显著性检验具体过程如下:

(1)

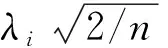
旋转经验正交函数(Rotating Empirical Orthogonal Function,简称REOF)方法是在EOF分解的基础上通过特征向量V进行最大方差旋转,当满足精度要求时则停止旋转,得到(2) 式。

X=BG

(2)

式中:X为旋转后的标准化矩阵;B为旋转后的特征向量;G为旋转后的时间系数。

旋转后的特征向量可以更加清晰地体现研究要素空间分布结构[22-23]。因此,本文采用REOF对山东省年降水场进行气候分区,并进一步分析研究各分区降水的时空特征。

1.2.2 赫斯特指数和重标极差分析法 赫斯特指数(下称Hurst指数)用于定量描述时间序列信息对未来对过去的长期依赖性,由英国水文专家H.E.Hurst提出。 Hurst指数的计算方法称为重标极差分析法(下称R/S分析法)[24],主要计算过程如下:

(1) 将时间序列xi(长度为N)均分为A个相邻的子区间(长度为n),表示为ea,a=1,2,…,A,ea为长度为N/A的子区间。

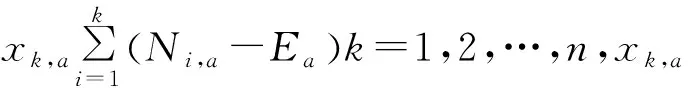
(3) 定义极差:Ra=max(xi,a)-min(xk,a),Ra为极差,即第(2) 步中累积截距最大值和最小值的差值。

(6)n从3开始,并重复1—5步,直到n=4,得到序列[R/S]n,n=3,…,N。

Hurst指数 用以描述(R/S)n和nH的正比关系,即

(R/S)n=C×nH

(3)

式中:C为常数。以lg(n)为解释变量,lg(R/S)为被解释变量进行线性回归:

lg(R/S)=lgC+H·lnn+ε

(4)

式中:ε为常数;H为Hurst指数的估值,即(4) 式的斜率,其具体形式见表2[25]。

表2 Hurst指数具体表现形式Table 2 Specific manifestations of the Hurst index

研究的时间序列是否为周期性循环及其平均循环长度可通过统计量V进行判断,统计量V的计算公式为:

(5)

在Vn～lnn的曲线上,若H=0.5,V统计量应该为一条水平线,若H<0.5,曲线向下倾斜,若H>0.5,曲线向上倾斜。曲线第一次出现的明显转折点对应的时间长度n就是未来对过去的依赖长度。

1.2.3 其他方法 运用ArcGIS软件,对统计量进行克里金插值分析,用以分析统计量空间分布特征;应用线性回归分析法分析降水的趋势性特征;应用Mann-Kendall(下称M-K)突变检验法分析降水的突变特征;应用Morlet小波分析降水的周期性特征;趋势分析、突变分析均采用α=0.05置信水平。

2 结果与分析

2.1 山东省年降水场EOF特征

对山东省年降水场进行EOF时空分解,并经North显著性检验,只有前2个降水模态显著,对应的特征值λ累计方差贡献率达到56.53%,能较好地代表山东省年降水的空间特征。对前2个降水模态进行REOF旋转后的方差贡献率和特征值均较旋转前更加均匀,详见表3。

表3 山东省年降水场EOF,REOF特征值及特征向量统计Table 3 Annual precipitation field EOF, REOF eigenvalues and eigenvector statistics in Shandong province

2.2 山东省年降水场REOF空间分布特征

对1991—2020年山东省年降水场REOF分解后,得到2个模态:第1模态空间分布表现为高值区主要集中在鲁东南沿海和泰沂山脉的迎风坡,该地区受海洋气候和西南暖湿气流影响比较明显,年降水量为729 mm,降水比较丰沛;第2模态的高值主要集中在鲁西北地区,该区主要位于泰沂山脉的背风坡,地形以平原为主,受大陆性气候的影响比较明显,年降水量616 mm,降水相对较少,其他地区主要为中部及南部部分山地丘陵地区,年降水量为717 mm,根据各模态荷载值大于0.6地区分布范围,经整理后可将山东划分为3个气候区(图2),按照模态顺序分别命名为东南沿海区(Ⅰ区)、西北平原区(Ⅱ区)、中部山地区(Ⅲ区)。

图2 山东省年降水REOF分解后得到的2个特征向量场空间分布(荷载值≥0.6)及降水分区

2.3 各降水模态的时间系数特征

从模态1和模态2的时间系数(图3)看出,其共同特征为:(1) 正值年份数少于负值,说明各模态降水偏少的年份更多。(2) 正值振幅相对较大,说明各模态降水偏多的年份降水强度更大。(3) 降水的年代际变化均较为明显,其中1990年代以降水偏少为主,2000年代以降水偏多为主,且偏多的强度较大,2010年代以降水偏少为主,且偏少的强度较大。但2个模态降水偏多偏少的年份分布及强度变化有所不同。

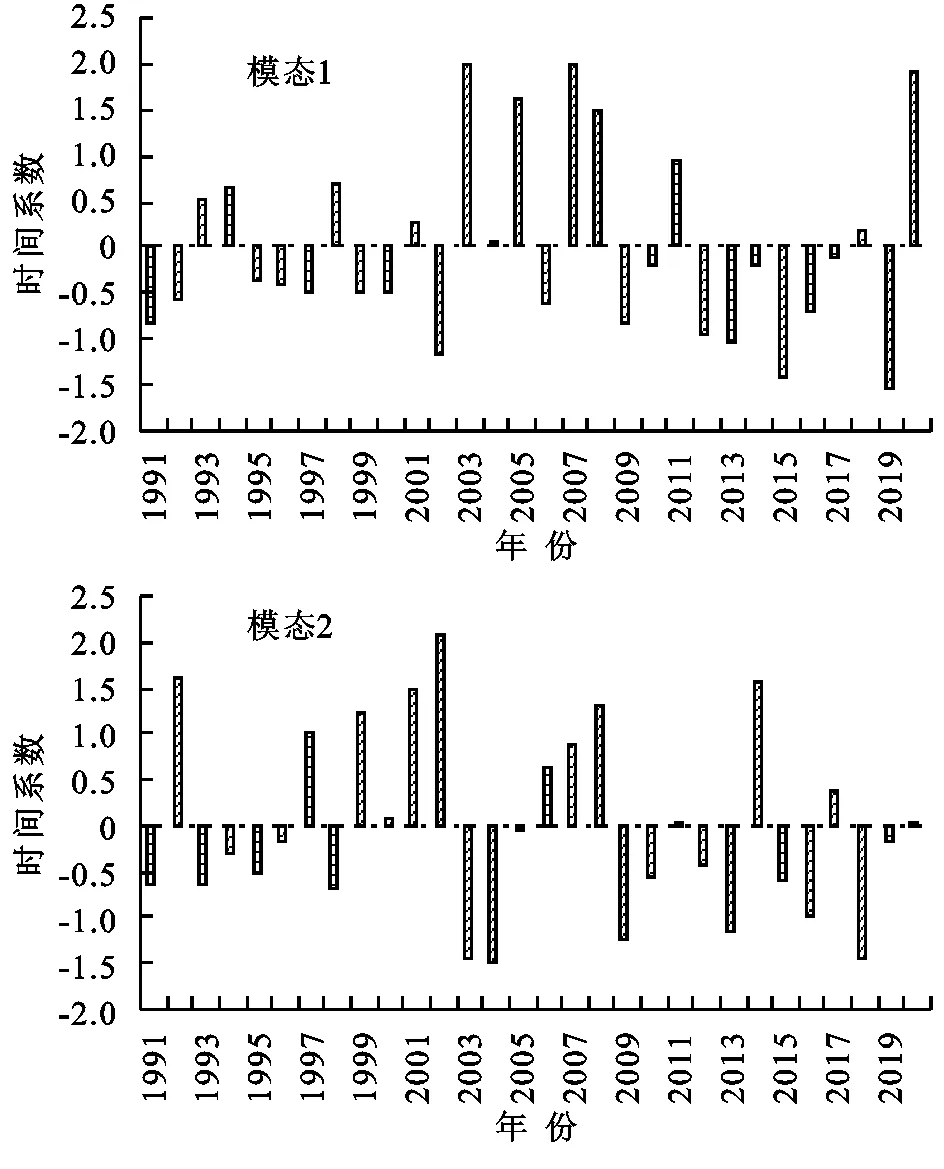
图3 山东省年降水场各模态特征向量时间系数

2.4 各分区降水的线性趋势及突变特征

图4A表明,东南沿海区(Ⅰ区)年降水呈不显著增加趋势(p>0.05),趋势率为11.5 mm/10 a,UF和UB曲线存在多个交点,主要发生在2000年代,各交点以后UF曲线变化均未通过α=0.05显著性水平,说明该区年降水突变不明显。

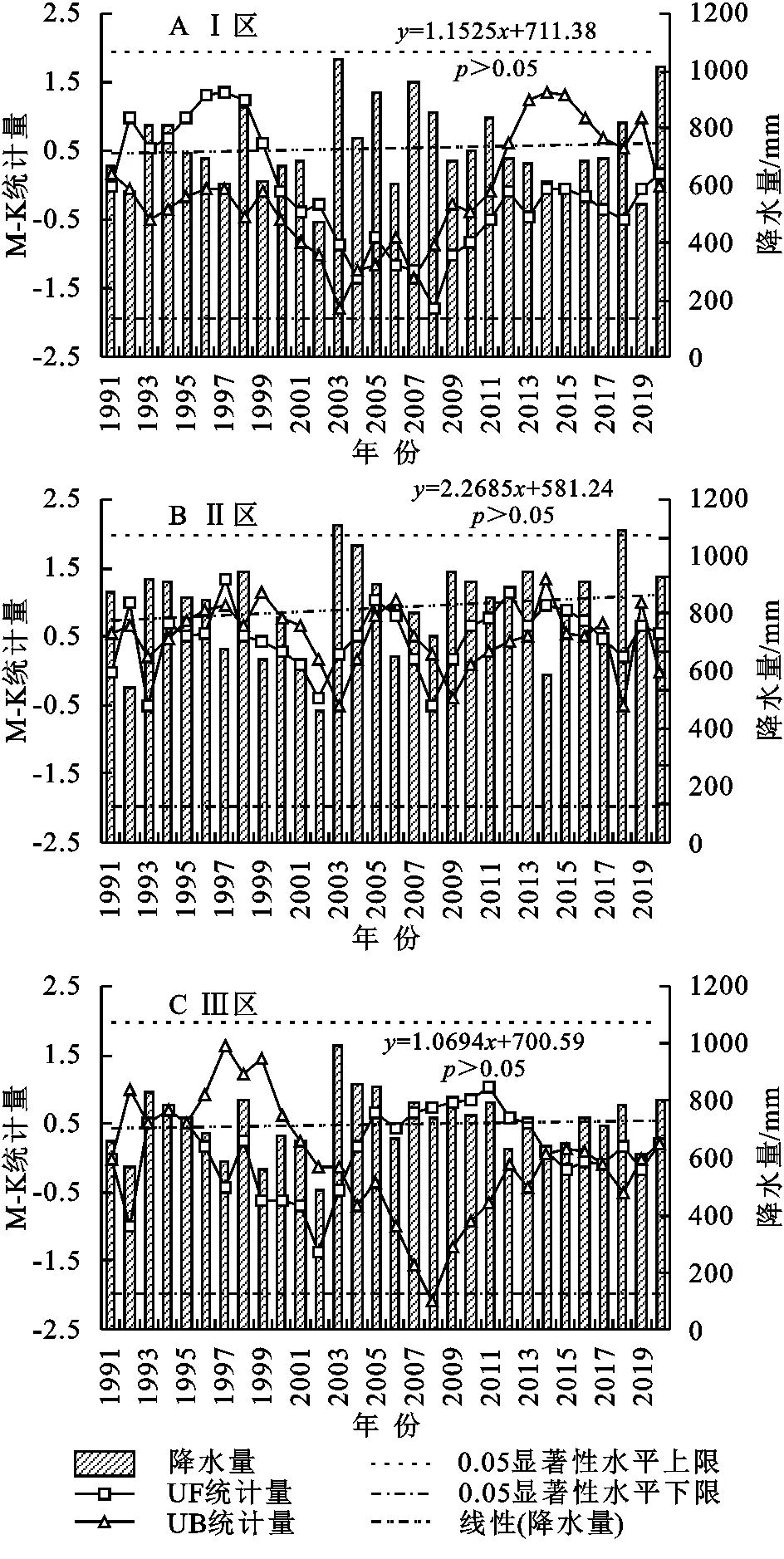
图4 山东省年降水各分区降水量线性趋势及M-K检验曲线

图4B表明,西北平原区(Ⅱ区)年降水量呈不显著增加趋势(p>0.05),趋势率为22.7 mm/10 a,UF和UB统计量存在多个交点,这些交点在各个年达均有发生,各交点以后UF曲线变化均未通过α=0.05显著性水平,说明该区年降水突变不明显。

图4C表明,中部山地区(Ⅲ区)年降水呈不显著增加趋势(p>0.05),趋势率为10.7 mm/10 a,UF和UB统计量存在多个交点,主要发生在1990年代前期、2003年及2010年代,各交点以后UF曲线变化均未通过 显著性水平,说明该区年降水突变不明显。

综上,山东省年降水量大致由东南向西北递减,各降水分区年降水均呈不显著增加趋势,且突变均不明显。山东省各分区年降水量主要为量的区别,变化趋势差别不大。

2.5 各分区降水的周期性特征

从图5可以看出:东南沿海区(Ⅰ区)年降水场存在2个较为明显的能量中心,中心尺度均为2～3 a,分别在2000年代中前期和2010年代后期表现最明显;西北平原区(Ⅱ区)年降水场存在3个较为明显的能量中心,中心能量从大到小依次为:中心尺度5～7 a,在1990年代后期和整个2000年代表现最强烈,中心尺度3 a,在1990年代后期到2000年代前期表现最强烈,中心尺度2～3 a,在2010年代后期表现最强烈;中部山地区(Ⅲ区)年降水场存在2个较为明显的能量中心,中心能量从大到小依次为:中心尺度2～3 a,在1990年代后期到2000年代中前期表现最强烈,中心尺度6 a,在2000年代中前期表现最强烈。

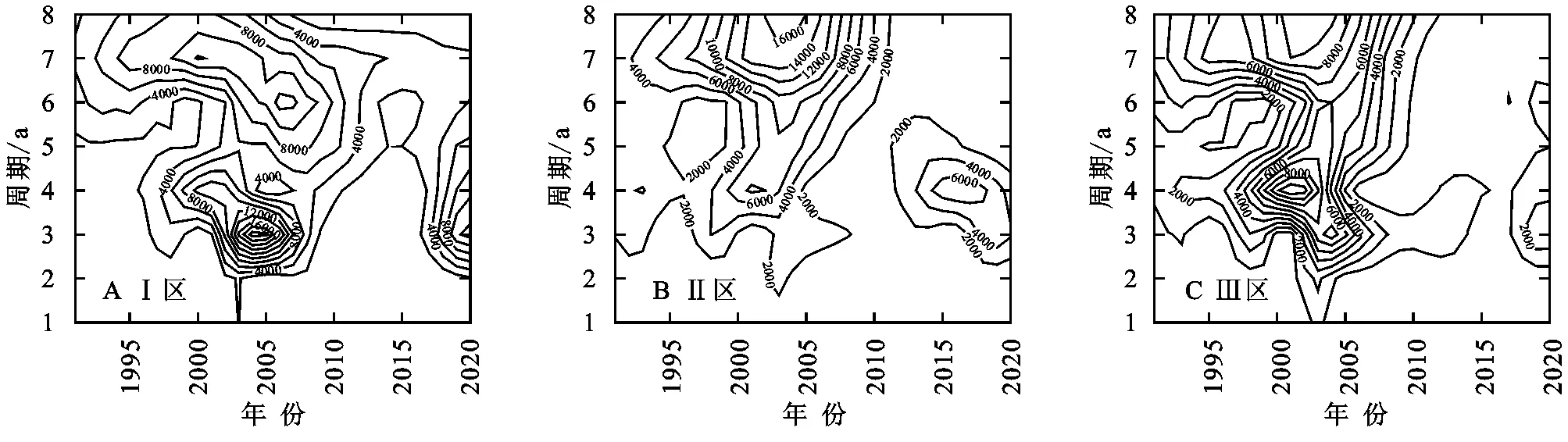
图5 山东省年降水场各分区小波系数模部平方等值线

2.6 各分区降水的未来趋势预测

对山东省各降水分区年降水未来趋势运用R/S分析法进行预测,东南沿海区(Ⅰ区)降水时间序列的Hurst指数0.72>0.65,表明Ⅰ区降水时间序列前后具有强持续性,即未来Ⅰ区年降水将继续呈现比较明显的不显著上升趋势;西北平原区(Ⅱ区)降水时间序列的Hurst指数0.5<0.59<0.65,表明Ⅱ区年降水量时间序列前后具有持续性,即未来Ⅱ区年降水量将继续呈现不显著上升趋势;中部山地区(Ⅲ区)降水时间序列的Hurst指数0.76>0.65,表明Ⅲ区降水时间序列前后具有强持续性,即未来Ⅲ区年降水将继续呈现比较明显的不显著上升趋势。

从图6可以看出:东南沿海区(Ⅰ区)降水V统计量第一个拐点的lnn≈1.79,对应的时间长度n≈6,说明Ⅰ区降水时间序列过去状态对未来状态的影响时间约为6 a,6 a后持续性将慢慢减弱直至消失;西北平原区(Ⅱ区)降水V统计量第一个拐点的lnN≈2.08,对应的时间长度n≈8,说明Ⅱ区年降水量时间序列过去状态对未来状态的影响时间约为8 a,8 a后持续性将慢慢减弱直至消失;中部山地区(Ⅲ区)降水V统计量第一个拐点的lnn≈2.30,对应的时间长度n≈10,说明Ⅱ区年降水量时间序列过去状态对未来状态的影响时间为约10 a,10 a后持续性将慢慢减弱直至消失。

3 讨 论

山东省各个降水分区降水均呈不显著增加趋势,这与《中国气候变化蓝皮书(2022)》[3]以及徐泽华等[14]的研究结论比较一致,但与卢仲翰[15]、程增辉等[26]的研究不一致,这与降水资料序列的时间范围差别较大、降水数据来源、站点密度等有较大关系。由于本文的降水序列时间尺度较短,降水的变化周期也相对较小,但10 a以下的降水周期与徐泽华[14]、程增辉等[26]的研究较为一致。本文选用的站点密度较大,资料序列较新,可以对山东省年降水场进行较为准确的分区,相关的分区结论可作为对前人研究成果继承和补充。

IPCC[1-2]和《中国气候变化蓝皮书(2022)》[3]都指出,中国高温、强降水等极端天气气候事件趋多、趋强的趋势更加明显。对于降水的研究也在逐渐从降水量转移到极端降水方面,未来应结合全球气候模型(GCM)及区域气候模式(RCM),利用观测数据对GCM/RCM基线期降水进行偏差矫正,开展对山东省极端降水事件的统计研究。

4 结 论

(1) 山东省各降水模态降水偏少的年份更多,降水偏多的年份降水强度更大,年代际变化均较为明显,其中1990年代以降水偏少为主,2000年代以降水偏多为主,且偏多的强度较大,2010年代以降水偏少为主,且偏少的强度较大,但各模态降水偏多偏少的年份分布及强度变化有所不同。

(2) 山东省年降水场划分为东南沿海区(Ⅰ区)、西北平原区(Ⅱ区)和中部山地区(Ⅲ区)3个区域。山东省年降水量大致由东南向西北递减,各降水分区年降水均呈不显著增加趋势,但趋势率各不相同,且突变均不明显。

(3) 山东省各降水分区年降水量均具有较为明显的周期性特征,其中东南沿海区年降水场存在2个较为明显的能量中心,中心尺度均为2～3 a,分别在2000年代中前期和2010年代后期表现最明显;西北平原区年降水场存在3个较为明显的能量中心,中心尺度分别为5～7 a,3 a和2～3 a,分别在1990年代后期和整个2000年代、1990年代后期到2000年代前期、2010年代后期表现最强烈;中部山地区年降水场存在2个较为明显的能量中心,中心尺度分别为2～3 a,6 a,分别在1990年代后期到2000年代中前期、2000年代中前期表现最强烈。

(4) 山东省各降水分区年降水量未来变化均具有持续性,其中东南沿海区(Ⅰ区)年降水量未来变化具有强持续性,过去状态对未来状态的影响时间约为6 a;西北平原区(Ⅱ区)年降水量未来变化具有持续性,过去状态对未来状态的影响时间约为8 a;中部山地区(Ⅲ区)年降水量未来变化具有强持续性,过去状态对未来状态的影响时间约为10 a.