Angular and planar transport properties of antiferromagnetic V5S8
Xiao-Kai Wu(吴晓凯), Bin Wang(王彬), De-Tong Wu(吴德桐), Bo-Wen Chen(陈博文),Meng-Juan Mi(弭孟娟), Yi-Lin Wang(王以林), and Bing Shen(沈冰),†
1Center for Neutron Science and Technology and School of Physics,Guangdong Provincial Key Laboratory of Magnetoelectric Physics and Devices,and Key Laboratory of Optoelectronic Materials and Technologies,Sun Yat-Sen University,Guangzhou 510275,China
2School of Integrated Circuits,Shandong Technology Center of Nanodevices and Integration,State Key Laboratory of Crystal Materials,Shandong University,Jinan 250100,China
Keywords: antiferromagnetism,planar Hall effect,magnetic and topological properties
1.Introduction
Antiferromagnet (AFM) materials have been considered as promising candidates for next-generation spintronic devices due to the scalability, robustness and ultrafast spin dynamics.[1]In an AF system, considering the special symmetry, the complicated magnetic correlations interacted with electron bands or phonon will host various exotic states driving novel transport properties as in ferromagnetic (AF)materials.[2]For example, recent studies revealed large anomalous Hall effect in noncolinear or topological AF systems such as Mn3Sn,[2]CoNb3S6,[3]or GdPtBi.[4]Spinpolarized current or magnetic spin Hall effect have been theoretically predicted and experimentally observed in Mn3Sn[5]and Mn3Ir.[6]With further consideration of the spin-symmetry,altermagnetic(AM)materials are identified with collinear AF order and exhibit unconventional spin-polarization order,providing new punch line for magnetism and spintronics.[7]Exploring the AF(or AM)magnetism in a two-dimensional(2D)or quasi-2D system will bring the dimension limitation which arouses types of novel magnetic or electronic states.[8,9]Such as in AF topological MnBi2Te4, the observed Chern state or axion state can drive quantized Hall conductance.[10]
For layered magnetic V-based chalcogenides(VmSn),tunable structural phases and magnetic properties via stoichiometric variations will bring a good platform to investigate interplay of magnetism and topology.[11,12]Bulk 2D VS2exhibits ferromagnetism and metallic behavior.[13]The doped or intercalated magnetic impurities with unfilled 3d orbitals act as the scattering centers leading to the appearance of Kondo effect due to the exchange interactions between localized magnetic moments of the impurities and conduction electrons.[14–16]The large vacancies of sulfur would make system evolve to another 1T1-phase V5S8with a fraction of the vanadium atoms inserted within the van der Waals gap between VS2layers (shown in inset of Fig.1(b)).In bulk V5S8,the AF state dominates the system;while with decreasing thickness, the AF state will evolve to a spin-glass-like state and eventually to a weak ferromagnetic state.[17–22]The interaction of spin lattice and electron would host the possible nonzero Berry curvature or exotic surface states.[23,24]The tunable magnetic anisotropy and correlations make V5S8a candidate for magnetic sensor which needs to investigate anisotropic magnetoresistivity(AMR)signal carefully for manipulating the spins in the AF system.On the other hand,recent study on VS2–VS superlattice revealed an unconventional planar Hall effect that persisted to 380 K.[25]This observation enlightens us to explore exotic properties in the similar compound such as V5S8,a natural VS2–V–VS2superlattice.In this paper, we investigate angular and planar transport properties of V5S8.Anisotropic AHE in a flopped state is identified with large Hall angleΘup to 0.1.The phase diagram reveals a spinflop vanishing line by rotating the applied field distinguishing the magneto-transport behaviors due to different magnon contributions.The prominent planar Hall effect (PHE) and anisotropic mganetoresistivity (AMR) are observed.By analyzing the plots of scaled PHE and AMR curves,the prominent AMR signal is attributed to the orbital effect instead of the nontrivial topological origin,but still promising for AF sensor.
2.Experimental details
Single crystals of V5S8were grown by the chemical vapor transport method using the pre-prepared V5S8powder as precursors and I2as the transport agent.The mixture of V5S8and I2were first heated at 500◦C (cold end) and 600◦C(hot end)in a two-zone furnace within five hours respectively and then kept for one week.Large plates of single crystals were harvested with a typical size of 2×2 mm2.The crystal structure and elemental composition were checked by x-ray diffraction(XRD)measurements and energy-dispersive x-ray spectroscopy(EDS),respectively.Figure 1(a)shows the(00l)peaks for our single crystals, indicating the good crystalline of our samples.The selected crystal was shaped into a rectangle for the transport measurements as shown in Fig.1(b).Six contacts were made by gold deposition to ensure a brilliant conductivity and the current was applied along theaaxis of the crystal.Electrical transport measurements were performed in a physical properties measurement system (PPMS Dynacool, Quantum Design).Magnetization measurements were performed in the vibrating sample magnetometer(VSM)module of the PPMS.
3.Results and discussion
3.1.Short-range magnetism and anomalous Hall effect
The temperature dependent resistivityρxx(T) exhibits a metallic behavior as shown in Fig.1(c) and an anomaly emerges aroundTAF= 30 K associated with the peak in temperature dependent susceptibilityχ(T) due to the AF transition.[19,26–28]With increasing temperature, the longrange (LR) AF orders vanish.A region dominated by shortrange (SR) magnetic orders fromTAFtoTθ=196 K is identified withχ(T) deviating the Curie–Weiss law.[29]The SR origin from magnetic fluctuation or frustration is widely observed in a magnetic system and may strongly affect its electron structure and transport behavior.Here,the frustrated parameter for V5S8is calculated byf=Tθ/TAF,[29]yielding a value of 6.175 indicating an intermediate magnetic frustration.
To explore the transport behaviors related to the AF and SR magnetic orders,field dependent magneto-resistivity(MRdefined asMR=(ρxx(µ0H)-ρ(0))/ρ(0)×100%)and Hall resistivityρxy(µ0H) are investigated at various temperatures as shown in Fig.2(a).In the AF state (belowTAF), nonlinear field dependent Hall effect and nonmonotonous field dependentMRare observed.At an intermediate fieldµ0HSF, a clear step emerges inρxy(µ0H)accompanied by a peak inMR,suggesting the occurrence of a spin-flop transition instead of possible breakdown of SDW or CDW transition consisted with previous work.[19,27]For a magnetic system,the Hall resistivity can be described as[30]
whereR0andRAare the ordinary and anomalous Hall coefficients, andMis the magnetization.The separatedρAxyat various temperatures are shown in Fig.2(c).In AF ground state, theρAxykeeps a small value while it increases sharply with a large Hall angleΘ= 0.15 compared to that in FM system after the spin-flop transition.For an AF system, it is usually surprising to host obvious AHE reminiscent with the recently observed prominent AHE in AF topological materials with large Berry curvature or chiral magnetic materials with non-vanishing magnetization.[31–33]For V5S8, the VIsite is located in the layer where the vanadium vacancies are ordered(vacant layer),while VIIand VIIIsites are in the layer without vanadium vacancies (full layer).Only the former contributes magnetism to the system.This conlinear AF ground state exhibits vanishing net magnetization,resulting in the negligible AHE and the positiveMR.However, the spin-flopped state gives rise to an increased magnetization, leading to the extended AHE and negativeMRdue to the delocalization by the flopped moments from VI.
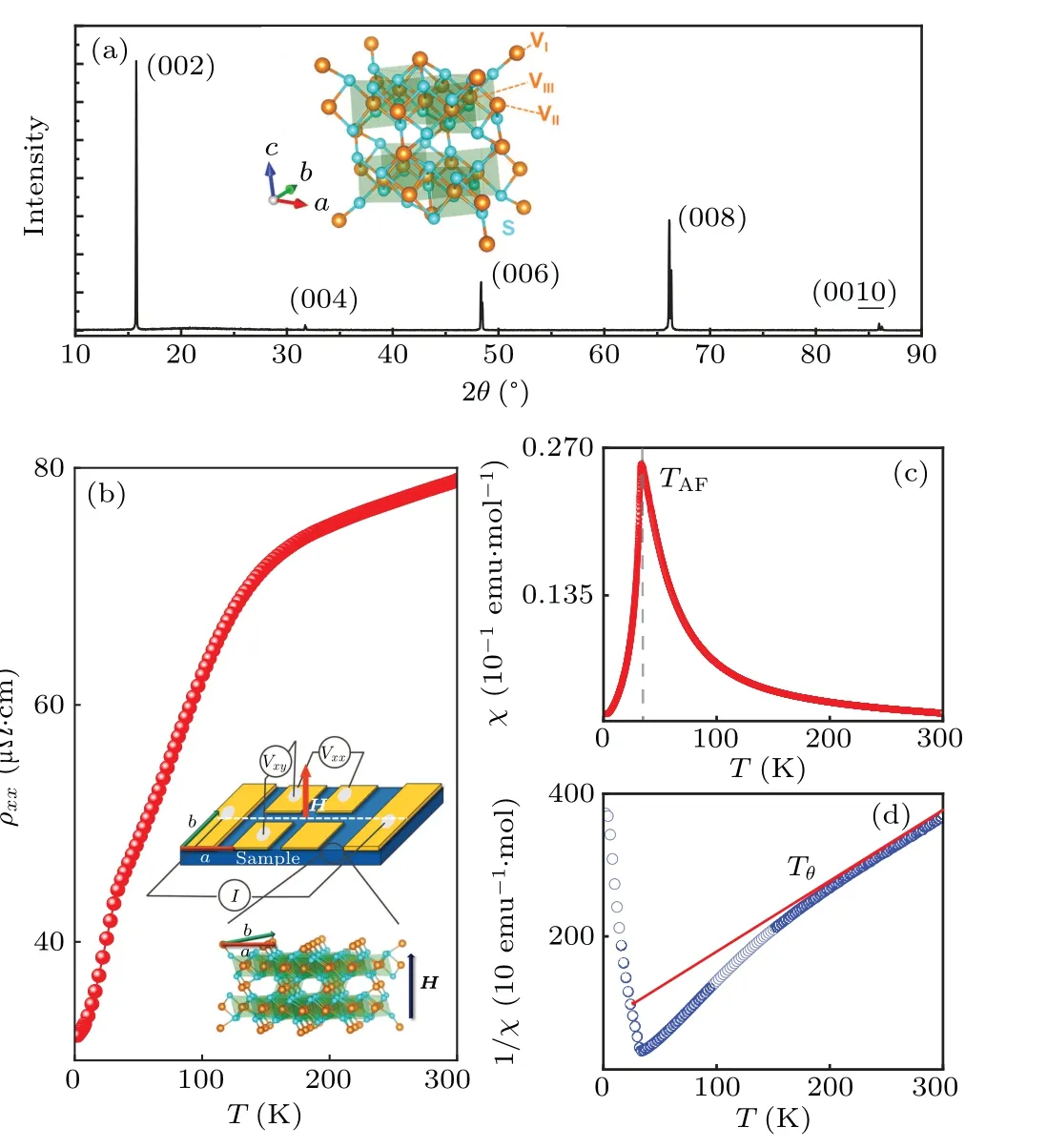
Fig.1.(a)XRD pattern of single-crystalline V5S8 with the corresponding Miller indices(00l)in parentheses.Inset:Crystal structure of V5S8.(b) Temperature-dependent longitudinal resistivity of V5S8 with the current(I)along the axis.Inset: Schematic for our electronic measurement device of V5S8.(c)Temperature dependent magnetic susceptibility of V5S8 withµ0H=1 T.(d)The inverse of magnetic susceptibility fitted by the Curie–Weiss law.

Fig.2.Field dependent ρxy (a) and MR (b) at 2 K, 5 K, 10 K, 15 K, 30 K,35 K, 40 K, 50 K with the applied magnetic field along the c axis of V5S8.(c)Anomalous Hall resistivity at different temperatures.(d)Field dependent magnetization curve at various temperatures.(e)The temperature dependent ordinary Hall coefficient RN (black)and anomalous Hall coefficient RA (red).(f)The phase diagram of V5S8 withµ0H‖c axis.The colors indicate anomalous Hall resistivity.Inset: Structure of V5S8 in the AFM phase.
With increasing the temperature aboveTAF, LR AF order vanishes and the SR magnetic order dominates the system.The nonlinear field dependent Hall effect and and AHE(observed in temperature dependentRAshown in Fig.2(e))can still persist in a narrow temperature region.The observed negativeMRindicates that the SR magnetic order in this region exhibits FM correlations probably driven by spin fluctuations or frustrations.These behaviors are reminisced with the observed AHE and unconventional AHE above AF transition in topological EuZn2As2[34]and EuCd2As2.[35]These results suggest that in a magnetic system,the SR order can play an important role in shaping the electron structure and driving exotic transport properties even without LR orders.The phase diagram for V5S8with the applied field alongcaxis is shown in Fig.2(f).Due to the SR magnetic order, AHE emerges aboveTAFand enhances with increasing the applied field.The negativeMRcan persist to even much higher temperature, indicating that this FM correlation exists in a wide temperature region.
3.2.Angular dependence of Hall effect and MR
To check the anisotropy in V5S8, angular transport measurements were performed with an applied field rotating in a plane perpendicular to the current direction (theaaxis) as shown in the inset of Fig.3(a).The nonlinear field dependent Hall effect and nonmonotonous field dependentMRsystematically evolve and exhibit anisotropic behavior as shown in Figs.3(a)and 3(b).The spin-flop transition atµ0HSFbecomes invisible gradually when rotating the applied field towards theaaxis.To better check the angular dependence of the spin-flop transition, the differentialρxycurves(dρxy/dµ0H)at various angles are acquired and plotted as the function of out-of-plane field componentµ0Hz=µ0Hcosθas shown in Fig.3(d).With tilting the applied field towardsabplane,HSFalmost does not shift and becomes invisible atθSF=50◦in consistent with the absence of the transition peak and positive response inMRcurves.The phase diagram for V5S8with the applied field rotating from thectoaaxis is shown in Fig.3(d).The spin-flop transition line roughly separates the system into two region:AFM region(I) and flopped magnetic region (II).In region I,the system keeps AFM structure with limited magnetization,leading to invisible AHE and the positiveMR.In region II,the flopped spins with FM correlations due to the applied field dominate the system,leading to visible AHE and negativeMRwith the appearance of the obvious magnetization.
In the AF groud state, the magnetic moments of VIin the(1 0 0)plane align ferromagnetically and are arranged like(up up down down) in the [1 0 0] direction, forming a staggered AF structure as shown in the inset of Fig.2(f).The direction of the moments is tilted about 10.43◦from thec-axis toward thea-axis.[28,36]Usually,the magnetic field affects the magnon spectrum by changing the Zeeman energy.[37]Thus,the magnonMRis determined by the component of the applied field along the magnetic easy axis.Our angularMR(especially for the flopped state) can not be simply scaled by a function ofµ0Hz.In V5S8, the magnetic easy axis is not strictly along thecaxis of the crystal.[36]Thus the slight tilt of the magnetization away from thezaxis by an in-plane field component would make the angularMRdeviate from empirical scaling.In this case, the magnonMRis proportion toMµ0H(cosθcosβ+sinθsinβ), whereMis the magnetization,θis the angle between the applied field direction andzaxis, andβis the angle between the magnetization direction andz.[38,39]With a smallβ,theMRcan be expressed as[37]
whereC1andC2are the coefficients independent of the applied field angle.The first part of this formula, following a linear field dependence, results from the magnetic moment,The second part, following a quadratic field dependence, can be well understood based on electron paramagnon scattering.C1andC2are acquired by fitting the above formula as shown in Fig.3(f).Withθ<θSF, the linear field dependent contribution mainly dominates theMRwhile the quadratic dependent contribution increases with tilting the applied field to theabplane.AtθSFwhere the spin-flop transition disappears,the linear field dependent contribution starts to decrease while the quadratic field dependent contribution becomes saturated.These behaviors reveal the magnetocrystalline anisotropy and anisotropic orbital scattering in V5S8.[40]

Fig.3.Field dependent MR (%) (a) and Hall resistivity ρxy(θ) (b) at 2 K with θ =0◦–90◦respectively.Inset of (a): The configuration of angular-dependent transport measurements for V5S8.The gray arrow indicates the rotating direction of the applied field.The current is along the a axis,and θ represents the angle between the applied field and c axis.(c)The phase diagrams in the polar coordinates with rotating applied field for V5S8.(d) dρscalexy /dµ0Hz at different angles.(e)The angular dependence of C1 and C2 described by Eq.(2).
3.3.Planar Hall effect and anisotropic magnetoresistivity
PHE and PAMR are transport phenomena driven by an in-plane magnetic-field-induced rotation of the principal axes of the resistivity tensor.[41]As shown in the inset of Fig.4(a),the applied field rotates within theabplane of the crystal for the measurements.Obvious PHE and PAMR exhibit two-fold oscillatory angular dependence as shown in Figs.4(a)–4(d).Usually the planar Hall and anisotropic mageto-resistivity can be described by


whereM‖is the in-plane magnetization andβis a constant.According to this formula,the amplitude ∆ρPxxshould be proportional to the in-planeM2‖.Though V5S8is an AF metal,the magnetization from canted AF moments by applied field induces prominent PHE especially for that in the high field region.With increasing the temperature,the decrease of ∆ρPxxis consistent with the rapid shrinking magnetization.Recently,the high-order oscillatory components of PHE and PAMR were observed in KV3Sb5[43]and Sr2IrO4films,[44]which suggests more complicated interaction such as magnetocrystalline anisotropy and spin–orbital coupling.For V5S8in all temperature regions, PHE and PAMR keep two-fold angular oscillations,indicating the origin from the spin-dependent scattering in the magnetic system.[43]
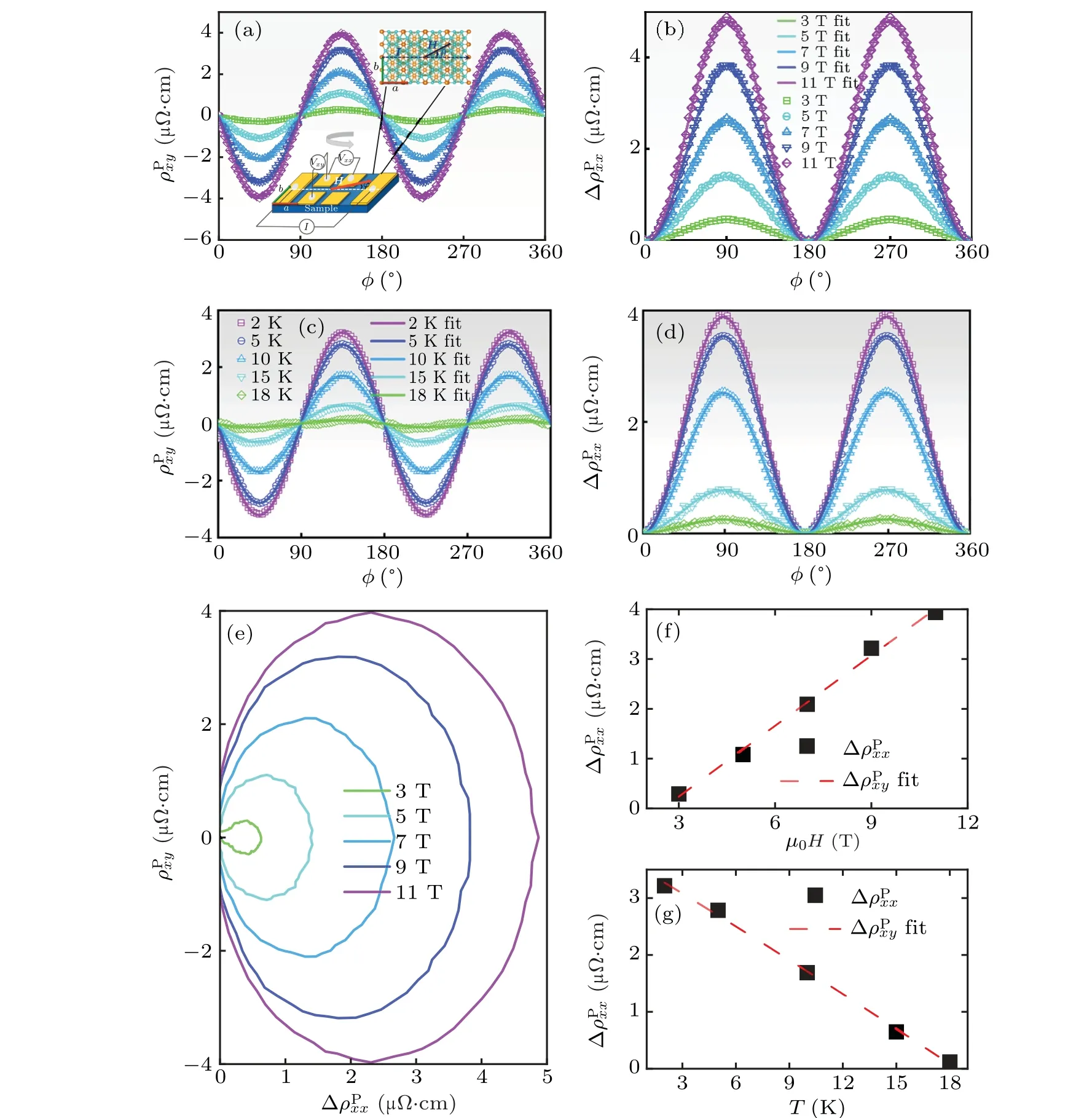
Fig.4.Planar Hall resistivity ρPxy(φ)(a)and anisotopic magnetoresistivity ∆ρPxx(φ)(b)at 2 K withµ0H=3 T,5 T,7 T,9 T,11 T,respectively.Inset of(a):The configuration of planar transport measurements for V5S8.The gray circular arrow indicates the rotating direction of the applied field.The current is along the a axis,and φ represents the angle between the applied field and current.The scatters represent the experimental data,while the curves represent the fitting results.Temperature dependent ρPxy(φ)(c)and ∆ρPxx(φ)(d)withµ0H=9 T at 2 K,5 K,10 K,15 K,18 K,respectively.(e)The parametric plots obtained by plotting ∆ρPxx(φ)and ρPxy(φ)with angle φ as the data for the x-axis and the data for the y-axis.The amplitude of planar resistivity at different magnetic field(f)and different temperature(g).
4.Conclusion
The angular and planar transport properties are systemically investigated for AF V5S8.Obvious AHE is observed in a flopped AF state with the Hall angle comparable to those in FM system.The SR magnetism makes AHE persist above the AF transition.The phase diagram by rotating the applied field reveals a spin-flop line with anisotropic Hall effect andMRfor different magnetic states, which can be attributed to the magnetocrystalline anisotropy and anisotropic orbital scattering.Prominent PHE and PAMR in V5S8exhibit two-fold angular oscillations systematically evolving with the temperature and the applied field,which is attributed to origin from the spin-dependent scattering.Our observations facilitate a deeper understanding of the interactions of magnetism and electron in V5S8and provide information for potential AF spintronic application as the magnetic sensors and nonvolatile memory devices.
Acknowledgements
Project supported by the open research fund of Songshan Lake Materials Laboratory(Grant No.2021SLABFN11),the National Natural Science Foundation of China (Grant Nos.U2130101 and 92165204), Natural Science Foundation of Guangdong Province(Grant No.2022A1515010035),Guangzhou Basic and Applied Basic Research Foundation(Grant No.202201011798), the Open Project of Guangdong Provincial Key Laboratory of Magnetoelectric Physics and Devices (Grant No.2022B1212010008), the Open Project of Key Laboratory of Optoelectronic Materials and Technologies (Grant No.OEMT-2023-ZTS-01), the National Key R&D Program of China (Grant Nos.2023YFF0718400 and 2023YFA1406500),and(national)college students innovation and entrepreneurship training program, Sun Yat-sen University(Grant No.202310359).
- Chinese Physics B的其它文章
- Unconventional photon blockade in the two-photon Jaynes–Cummings model with two-frequency cavity drivings and atom driving
- Effective dynamics for a spin-1/2 particle constrained to a curved layer with inhomogeneous thickness
- Genuine entanglement under squeezed generalized amplitude damping channels with memory
- Quantum algorithm for minimum dominating set problem with circuit design
- Protected simultaneous quantum remote state preparation scheme by weak and reversal measurements in noisy environments
- Gray code based gradient-free optimization algorithm for parameterized quantum circuit

