Exact solutions for magnetohydrodynamic nanofluids flow and heat transfer over a permeable axisymmetric radially stretching/shrinking sheet

U.S.Mahabaleshwar, G.P.Vanitha, L.M.P´erez, Emad H.Aly, and I.Pop

1Department of Studies in Mathematics,Davangere University,Shivagangothri,Davangere,India

2Departamento de F´ısica,FACI,Universidad de Tarapac´a,Casilla 7D,Arica,Chile

3Department of Mathematics,Faculty of Education,Ain Shams University,Roxy,Cairo,Egypt

4Department of Mathematics,Babes-Bolyai University,400084 Cluj-Napoca,Romania

Keywords: magnetohydrodynamic,nanofluid,stretching/shrinking sheet,axisymmetric flow,analytical solution,suction/injection

1.Introduction

In the recent years,different techniques,including the use of micro-channels, expanded surfaces, and surface vibration,can be used to improve the capacity for heat transfer.The most crucial factor for determining a fluid’s capacity for heat transfer among all other qualities is heat conductivity.The type and shape of nanomaterials determine nanofluids’thermal conductivity.The fluid’s higher thermal efficiency will result in less energy loss,which can further lower costs and boost output in industrial applications.Choi[1]was the first to introduce the idea of nanofluids,where he suggested suspending nanoparticles in pure fluids(water,glycol or engine oil).In an effort to explain why the thermal conductivity of these fluids increased,Buongiorno[2]created a model that included particle Brownian motion and thermophoresis.The use of metals in thermal systems is appropriate since, as is well known, their capacity to transfer heat is 100 times greater than that of liquids.[3–7]The thermal performance of nanofluids was numerically investigated by taking unsteady flow into account and developing the model for diamond-water and silver–water nanofluids,as described by Adnanet al.[8]The CuO–water nanofluid friction factor was studied by Chavdaet al.[9]on various pipes,and they discovered that the friction factor increased as the volume flow rate of CuO–water nanofluid increased.Heat and mass transfer rate due to flow of nanoparticles over a stretching surface is analytically analyzed by Vanithaet al.[10]Researchers discovered that using nanoparticles in the design of energy storage produced better results.[11]

A review of the literature finds that axisymmetric flows produced by radially extending surfaces have received less attention.The study on boundary-layer flow over a stretching surface appears to have been started by Sakiadis,[12]who also modeled the boundary-layer equations of two-dimensional(2D)axisymmetric flow.Many authors have conducted a significant number of investigations on this issue from various angles.By using the Galerkin least squares approach, Martinset al.[13]investigated the effects of inertia and shear thinning on the axisymmetric flows of Carreau fluid.They then compared their numerical results with the previous studies and discovered that they were in very good agreement.Alhamalyet al.[14]reported heat transfer and axisymmetric stagnation point flow of nanoparticles on linearly extending surfaces.The problem of slip as well as partial slip effects on the axisymmetric flow and electrically conductive fluid flowing across a sheet that is stretching out have been studied,[15–17]in order to obtain an exact and numerical solution.

Heat exchangers, power pumps, generators, and electrostatic filters are examples of the numerous devices that incorporate magnetohydrodynamics.Theoretically,magnetic fields can cause a drag in a fluid called the Lorentz force, which slows down the fluid movement and therefore raises the temperature of the fluid.Therefore, using the magnetic field to delay the separation of the boundary layer is practical.The effect of magnetic parameters,particularly in the boundary layer flow problem,is the subject of extensive investigation.By taking into account various fluids while employing various parameters, Mahabaleshwaret al.[18,19]worked on magnetohydrodynamic (MHD) fluid flow with heat transmission.The examination of MHD axisymmetric flow of hybrid nanofluid and energy transfer on a nonlinearly stretched/shrinked surface with thermal radiation was carried out by Khanet al.[20]The same analysis with joule heating was examined by Najiyahet al.,[21]see also Refs.[22–25].

With the remark of the above literature, the present work focuses on examination of MHD axisymmetric flow of Al2O3and Cu nanoparticles suspended in H2O past a stretched/shrinked sheet.The boundary layer governing equations are reduced to ordinary differential equations by utilizing the suitable similarity conversions.In the current study,the performance of Al2O3–H2O nanofluid is compared with the Cu–H2O nanofluid for velocity and thermal fields and presented in the graphs.The effects of several physical characteristics, including the magnetic parameter, the stretched/shrinked parameter, Prandtl number and solid volume fractions respectively are also discussed.In addition to this,the physical quantities like skin friction and Nusselt number are evaluated and plots are drawn.

2.Mathematical framework

Consider a 2D MHD axisymmetric flow of nanofluid past a radially stretched/shrinked sheet,as shown in Fig.1.

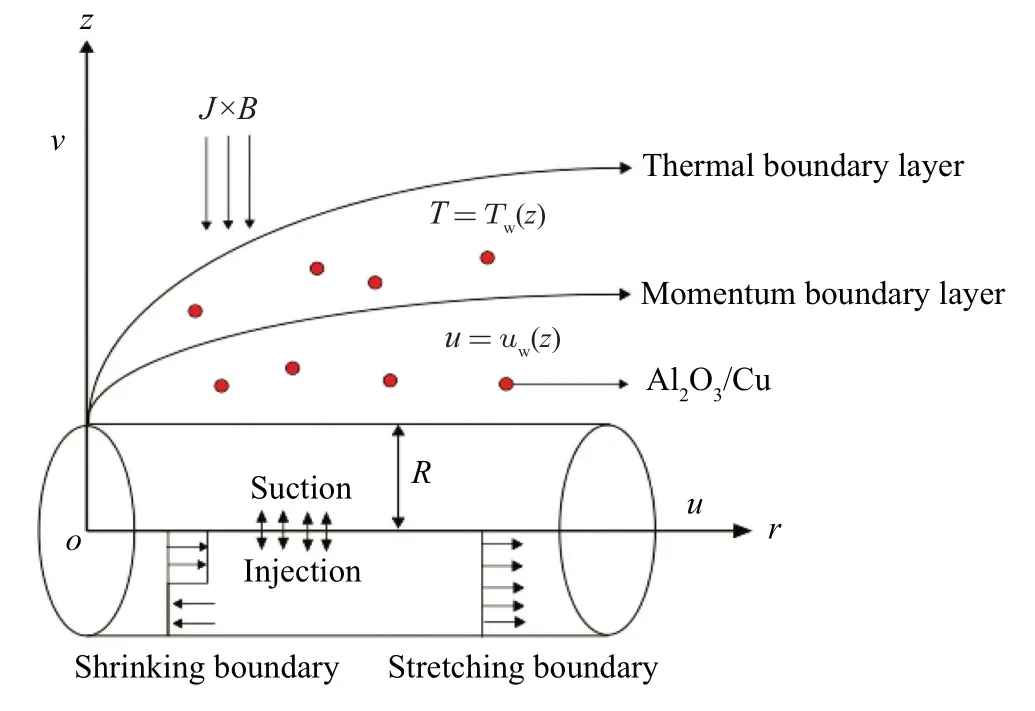
Fig.1.Physical model representation.

Here (r,ϕ,z) are the Cartesian cylindrical coordinates with(r,ϕ)-axes taken in the plane surface of the sheet which is perpendicular tozaxis, the flow is acrossz ≥0.The flow being axisymmetric all variables satisfy the condition∂/∂ϕ= 0.The velocity of the stretched/shrinked sheet isuw(r)=ur(r)λ=ar3λ,whereais a fixed positive constant.The termvwis the velocity of the constant mass flux withvw< 0 (suction) andvw> 0 (injection), respectively.Further, an intensity of the varying magnetic field is assumed to beB(r)=B0reacts perpendicular to the sheet,whereB0is the strength of the applied magnetic field.The surface temperature of the sheet isTw,whileT∞is the uniform temperature of the far flow.The water based fluid is a nanofluid(H2O)containing nanoparticles Al2O3/Cu.Furthermore, the basic fluid with the suspension of nanoparticles is considered to be in an equilibrium condition of temperature, that the nanoparticles have a uniform size and shape, and that they are in a state of thermal equilibrium.

Under these presumptions,the following set of boundarylayer equations governing the nanofluids’continuity,velocity,and heat is represented in Cartesian cylindrical coordinates:(see Shahzadet al.[26]and Devi and Devi[27])

Here(u,v)denotes velocity constituents along the(r,z)plane of the surface of the sheet,Ttaken as sheet temperature, andλas stretched/shrinked parameter withλ>0 for the stretched flow,λ<0 concerns the shrinked sheet andλ=0 is considered for the steady case.

Furthermore,µnfis the known as dynamic viscosity,ρnfrepresents density, (ρCp)nfis the nanofluid heat capacitance withκnfrepresents thermal conductivity, defined as in Ref.[28]by Hoet al.and Ref.[29]by Sheremetet al.

Hereφis known as nanoparticle volume fraction,φ=0 is analogous to a basic fluid with the densitiesρfandρs,κfas well asκsare the thermal conductivities (ρCp)fwith (ρCp)sare referred heat capacitances of H2O and at constant pressure specific heat is given byCp.

The thermophysical characteristics for the base fluid and nanoparticles are listed in Table 1.

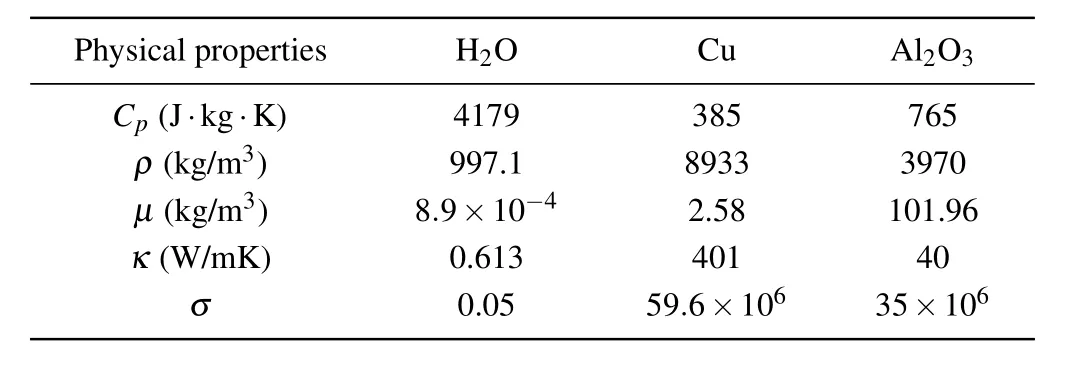
Table 1.Thermophysical characteristics for the base fluid and nanoparticles(Ahmed et al.[30]).

Introducing the following similarity transformations,which are inspired by the boundary conditions Eq.(4)

Using Eqs.(6)and(11),we obtain,

The non-dimensional velocityf′(η) is deduced from the equivalent altered quantitiesF′(z) simply asf′(η) =F′(z)and the non-dimensional wall skin frictionf′′(0)together with the energy fluxθ′(0)since the sheet yields the relevant quantitiesF′′(0) withG′(0) of the rescaled issues as specified by the relations

Following Shahzadet al.,[33]the solution of Eq.(14) is expressed as

where Γ is the gamma function,see Whittaker and Watson.[34]

3.Stability analysis

A thorough analysis of the stability of dual solutions of the nanofluid flow is performed over the stretching and shrinking sheet using dominating expressions, namely Eqs.(8) and(9) and the corresponding boundary constraints in Eqs.(10a)and(10b).Merkin[35]first presented an analysis of the stability of dual solutions,demonstrating that a positive eigenvalue is more stable and reliable than a negative eigenvalue.Assessment of the stability of dual solutions of the stream at the stagnation point in a pore-filled medium is carried out by Harriset al.[36]Later on, many investigations demonstrated the stability of the dual solutions.

Assume that the nanofluid flow in a transient condition as it shrinks or stretches a sheet.Equations corresponding to the problem of unstable nanofluid flow Eqs.(2)–(4)are presented as follows:

Using the newly developed similarity transformations, i.e.,Eq.(24)into Eqs.(22)and(23),it has been possible to solve the following system of differential equations:

Along with boundary conditions:

Note that,F(η) =F0(η) andθ(η) =θ0(η) are included in the model, appropriate nanofluid patterns over the stretched/shrinked sheet have the following unstable form

In Eq.(28),f(η,τ)andφ(η,τ)are considered to be smaller thanF0(η) andθ0(η).An unsteady solutions of the existing issues,i.e.,the unbounded values of the eigenvaluesγare produced by Eqs.(25)and(26)sayγ1<γ2<γ3···.Initial decline of the instabilities is accompanied by positive eigenvalues,whereas initial rise of the instabilities is accompanied by negative eigenvalues,suggesting that the nanofluid flow across the surface is stable.Along with the boundary conditions,the governing differential equations have the following unstable form

whereτ=0 is the steady state.Now, by replacingf(η)=f0(η) andφ(η)=φ0(η) in Eqs.(29) and (30), the following eigenvalue problem and the imposed boundary conditions is gained:

For specific values ofM,η,γ,andPr,the stability of the dual solution, i.e.,F0andθ0are evaluated during the least eigenvalue.

4.Results and discussion

Using the graphical representation, the study of the axisymmetric nanofluid flow and heat transfer properties and the existence of the dual solutions across a radially shrunk sheet has been addressed in this section.The physical interpretation of the nanofluid fluid flow and heat transfer over the radially stretching/shrinking sheet is obtained, along with a thorough discussion of the findings.The dual solutions[38]depicted in Figs.2–8 provide an illustration of the effects of different emerging parameters on the velocity, temperature, and skin friction of the nanofluid.These parameters include magnetic,solid volume fraction, and suction/injection.The graphs also depict the comparison study between Al2O3–H2O and Cu–H2O nanofluids.Further, the results are also compared with the previous results.Whenφ=0,i.e., for the regular fluids,the present results hold good with the results of Shahzadet al.[32]Also, with the absence of the magnetic effect, the current work is in good agreement with the results of Magyari.[31]

4.1.Stretching sheet

Animpactof the magnetic field (M) on the velocity and energy profiles is illustrated in Figs.2(a)and 2(b).As the magnetic parameterMis increased, it can be seen from Fig.2(a)that the magnitude of the dimensionless radial component of velocity decreases.This demonstrates how the Lorentz force slows fluid motion in the radial direction, which causes a reduction in boundary layer thickness.Therefore,the magnetic field enables a way to regulate the thickness of the momentum barrier layer.Further analysis from Fig.2(b) reveals that the temperature of the fluid reduces as the magnetic parameterMincreases.Furthermore, we notice that the Al2O3nanoparticles move faster towards the surface compare to Cu because the density of Al2O3is less than the Cu.The fluid temperature of Al2O3is more than Cu.

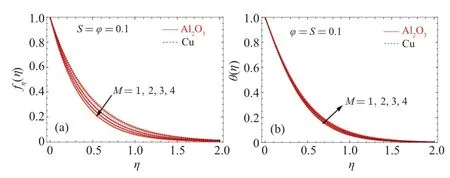
Fig.2.An impact of M on(a)the velocity profile and(b)the energy profile.

An impact ofϕ(solid volume fraction) on the velocity and energy profiles is depicted in Figs.3(a) and 3(b).On a stretched surface the fluid momentum and thermal boundary diminishes with the increased value of the volume fraction parameter (ϕ).Furthermore, the Al2O3nanoparticles move faster towards the surface in comparison with Cu because the density of Al2O3is less than Cu.The fluid temperature of Al2O3nanofluid is more than Cu nanofluid.

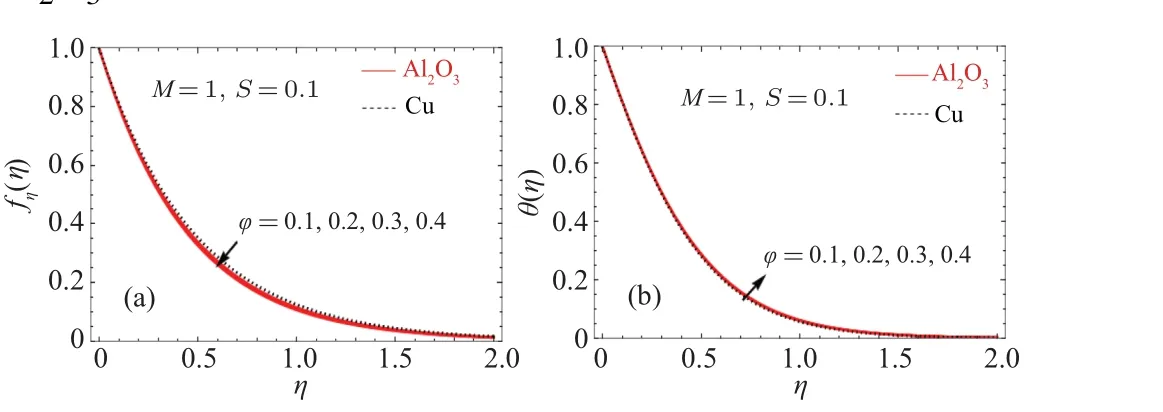
Fig.3.An impact of volume fraction parameter(ϕ)on(a)the velocity and(b)the energy profile.

Figures 4(a) and 4(b) demonstrates the impact of mass transpirationSon the velocity and temperature profiles.It is observed that due to increase in the value ofS,the velocity of the fluid and heat transfer decreases.

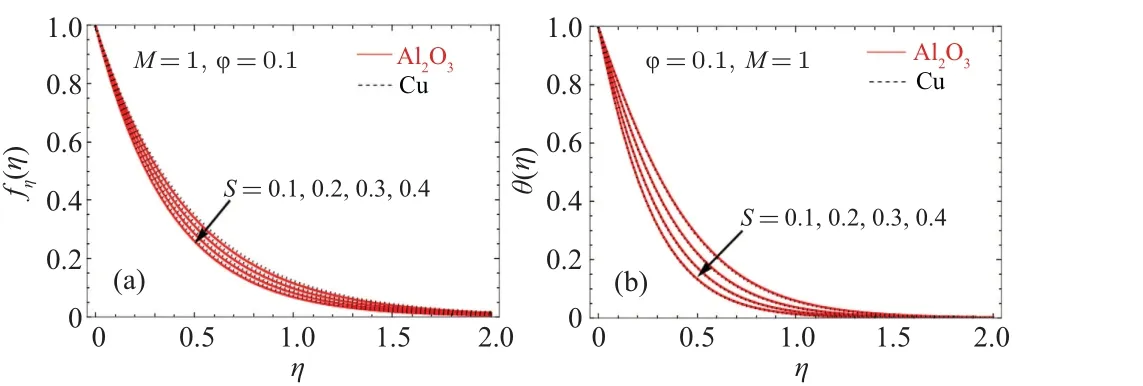
Fig.4.An impact of mass transpiration(S)on(a)the velocity and(b)the energy profile.

Figure 5 shows the sketch of Nusselt number for varying volume fraction.It illustrates that when volume fraction (ϕ)is increased,it leads to the enlargement of the boundary layer partition.

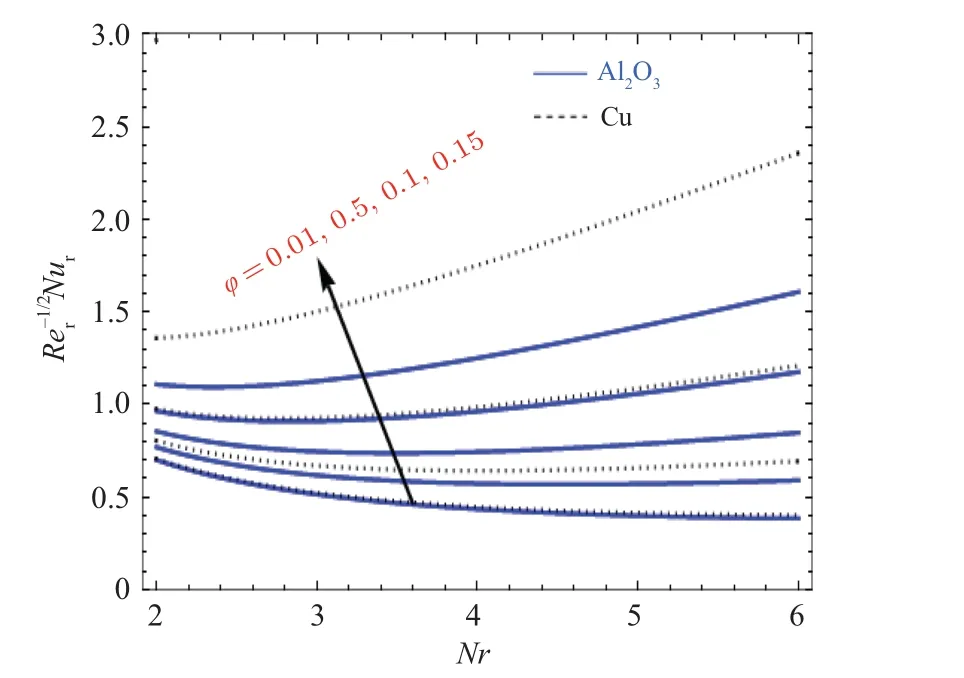
Fig.5.Deviations of Nusselt number Re-1/2r Nur with radiation parameter for various values of φ.

4.2.Shrinking sheet

The shrinking sheet case has two possible solutions based on the+and-signs of Eq.(20),forβ1,β2,and the solution branches are known as the upper and lower branch solutions,in the study we take it as first solution which is represented in solid line and dotted line and the second solution which is represented in blue solid line and orange dotted line.

An impact ofϕon the velocity and energy profile is shown in Figs.6(a) and 6(b).On a shrinking surface, by increasing volume fraction parameter (ϕ) the fluid velocity in the first solution decreases and opposite behavior is observed in the second solution and thermal boundary layer increase for both solutions.

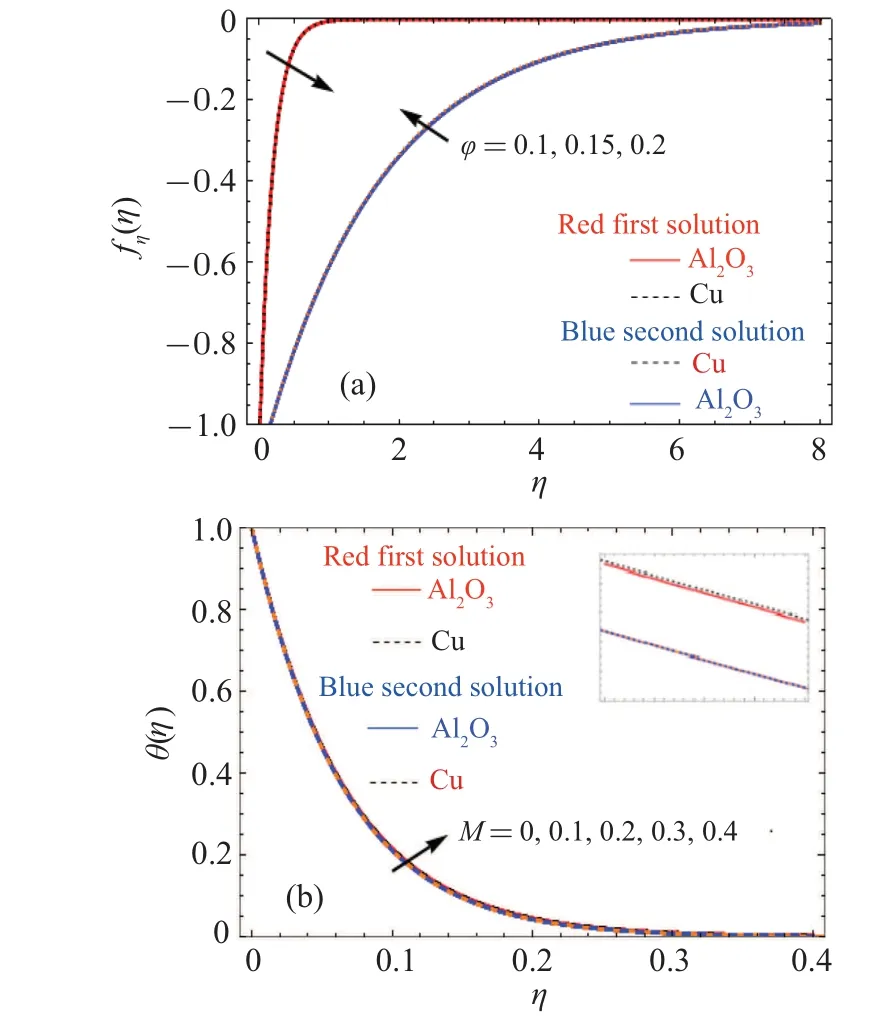
Fig.6.An impact of solid mass fraction parameter(ϕ)on(a)the velocity and(b)the energy profile.

The mass transpiration parameter(S)affecting the velocity with temperature profiles is shown in Fig.7.On a shrinking surface,by increasing mass transpiration(S),fluid velocity rises in the first solution and falls in the second solution along with both solutions result in a thermal boundary layer reduction.

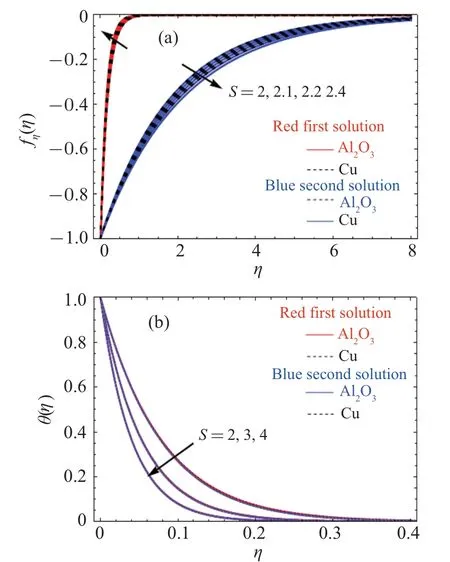
Fig.7.An impact of mass transpiration parameter (S) affecting (a) the velocity and(b)the energy profiles.

Figure 8 depicts an influence of the magnetic parameter(M) on the velocity and energy profiles.On a shrinking surface, by increasing magnetic parameter (M) in the first solution, fluid velocity grows up and reduces in the second solution.Whereas thermal boundary layer is found to rise for the first solution but to decrease in the second solution.

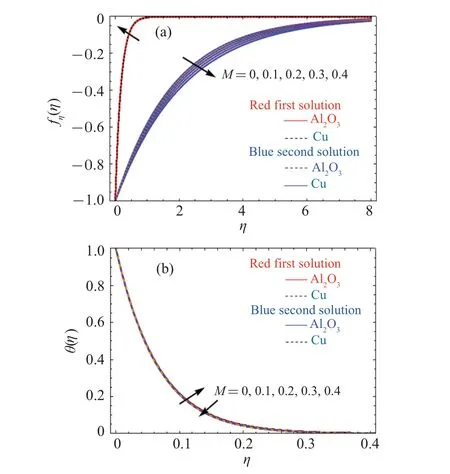
Fig.8.An impact of M parameter affecting(a)the velocity profile and(b)the energy profile.

Fig.9.Deviations of skin friction Re1/2r Cf with mass transpiration parameter for various values of φ: (a)Al2O3–H2O and(b)Cu–H2O.

The relationship between theSandRe1/2fCfskin are displayed for the investigated nanofluids in Figs.9(a) and 9(b).The coefficients of skin friction are deteriorating in the presence of mass suction of the nanofluids on the sheet as the solid volume fraction parameter values increase.When comparing the streamline profiles for mass suction and mass blowing, it is observed that the skin friction coefficient is higher for the mass suction.It is noted that skin friction of the Al2O3–H2O nanofluid is deteriorating faster when compared to Cu–H2O nanofluid.

5.Concluding remarks

In the present study, we examined the boundary-layer flow and heat transfer characteristics brought about by Al2O3–H2O and Cu–H2O nanofluids over a sheet that was either stretching or contracting in relation to magnetic phenomena.The gained transmuted similarity nonlinear ODEs are then analytically solved.Graphs were used to illustrate and debate various dimensionless physical characteristics that influence the velocity and energy of the flow.Following are the summaries of the closing comments.

(i) Existence of dual solution is found for shrinking sheet and unique solution for stretching sheet.

(ii) By raising the value of the parameterSin the stretching situation,the velocity of fluid and thermal boundary layer decrease.

(iii) An increased value ofMon the stretching scenario,the velocity of fluidfalls and thermal boundary layer grows.

(iv) By increasing the value ofϕ,the fluid velocity in the first solution decreases and the conflicting behaviors seen in the second solution.

(v) On raising the value ofM, the fluid velocity in the first solution increases and decreases in the second solution.

(vi) The thermal boundary layer decrease for both solutions by increasing the value of parameterϕandSon shrinking case.

(vii) By raising the value of the parameterMin the shrinking case,the thermal boundary layer increases in the first solution and reduces in the second solution.

(viii) Compared to Cu–H2O nanofluid, Al2O3–H2O nanofluid has significant improvements in the thermal characteristics of the fluid.

(ix) In the future work,the authors will extend the present work to hybrid nanofluids,see for example Refs.[38–40].

It should be noted that the above obtained remarks refer that, in the case of shrinking sheet, the first solutions of the stream are stable and physically realizable, whereas those of the second ones are unstable.

Acknowledgments

LMP acknowledges financial support from ANID through Convocatoria Nacional Subvenci´on a Instalaci´on en la

Academia Convocatoria A˜no 2021,Grant SA77210040.