Electronic property and topological phase transition in a graphene/CoBr2 heterostructure
Yuan-Xiu Qin(秦元秀), Sheng-Shi Li(李胜世), Wei-Xiao Ji(纪维霄), and Chang-Wen Zhang(张昌文)
School of Physics and Technology,Institute of Spintronics,University of Jinan,Jinan 250022,China
Keywords: van der Waals heterostructure, in-plane magnetic anisotropy energy, quantum anomalous Hall effect
1.Introduction
Graphene, a pioneering two-dimensional (2D) hexagonal honeycomb lattice material, attracts a great deal of attention for its excellent electronic, mechanical and optical properties.[1–3]In particular, among graphene’s many properties, its topological properties are of interest due to its potential application in spintronics.[4–6]Up to now,the theoretical exploration of self-supported graphene has been extensive,prompting a shift in focus to graphene applications and the hope of making breakthroughs in graphene-based devices.
The weak intrinsic spin–orbit coupling (SOC) and lack of an orbital band gap in graphene hinder its further application.[7–10]However, the emergence of 2D van der Waals (vdW) opens up possibilities for utilizing graphene in various applications.Due to its sensitivity to the interlayer distance, the proximity effect in 2D vdW heterostructures offers a controllable way to adjust the electronic band structure of materials.[11–19]Significantly, vdW monolayers, unconstrained by the limitations of lattice matching,can be readily assembled into vdW heterostructures with arbitrary designs.[20–25]Moreover, the accumulation and hybridization properties of heterostructures constructed of 2D vdW materials are higher than those of the corresponding monolayer.[26–31]For instance, according to a recent experiment, the intrinsic SOC of graphene on SiO2is determined to be 20 µeV, which is higher than the value for pristine graphene (12 µeV).[32,33]Furthermore, it has been reported that vdW heterostructures have been used to obtain significant progress in achieving topological phases in graphene such as graphene/CrI3.[34–36]In vdW heterostructures, time-reversal symmetry is broken by the presence of magnetic exchange and,combined with SOC,results in and the quantum anomalous Hall effect (QAHE),[37–40]i.e., time-reversal symmetry protects topological edge states, leading to topological protection as determined by Chern numbers.[34,35,37,41,42]Noticeably,some low-power-consumption spintronic devices can be designed based on the tunable dissipationless chiral edge state.
As for devices, the uniaxial magnetic anisotropy also plays a significant role.Recently, research has demonstrated that manipulation of the interlayer spacing in vdW heterostructures can effectively regulate perpendicular magnetic anisotropy(PMA),as exemplified by the graphene/NiI2(Gr/NiI2) system.[43]The PMA of NiI2is significantly enhanced by decreasing interlayer distance, which is conducive to realizing low-power spintronic devices.[43–47]In addition,2D materials with in-plane magnetic anisotropy (IMA), such as 2DXYmagnets CoBr2and CrCl3, have many excellent properties and application prospects.[44,48–50]However,in comparison to PMA, IMA has received significantly less research attention.To explore the variation of IMA and QAHE by decreasing the interlayer distance of vdW, in this work,we provide a systematic theoretical analysis of the electronic and magnetic structures in a Gr/CoBr2heterostructure from first-principles calculations.Studies show that the CoBr2monolayer is an intrinsically ferromagnetic(FM)semiconductor with IMA, belonging to the 2DXYmagnet family with a Kosterlitz–Thouless phase transition temperature(TKT)=23.8 K.[49]By analyzing the magnetic anisotropy energy(MAE)and density of states(DOS),we find that the MAE increases as the interlayer distance of Gr/CoBr2decreases and IMA,enhanced due to the interaction of Co-d orbitals,is modified by its proximity to graphene.Remarkably,decreasing the interlayer distance can lead to exchange splitting and a gap in the electronic band structure of graphene.Naturally, we also evaluate the topological characteristics of Gr/CoBr2when taking the SOC into account and the findings reveal the existence of the QAHE.Moreover, we design a device that suggests a pathway for novel low-power spintronic devices.
2.Computational details
We performed first-principles calculations using densityfunctional theory as implemented in the Viennaab initiosimulation package.[51–53]The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof realization was adopted for the exchange–correlation functional.[54]Considering the solid Co 3d electronic correlation effect in CoBr2, the GGA +Umethod is adopted (U= 5 eV,J=0.0 eV).[43,49,55–57]The cutoff energy for the plane-wave base expansion is set to 500 eV.It is good enough to sample with aΓ-center 11×11×1k-point grid for the Brillouin zone and a center 25×25×1 grid for the magnetic anisotropy calculation.Naturally, the MAE is calculated based on the energy variations between the in-plane and out-of-plane spin direction after considering SOC.The convergence criterion of the parameter for energy is 10-6eV,and the criterion also requires the Hellmann–Feynman force acting on each atom to be less than 10-3eV/˚A.The vacuum space is set to 25 ˚A in thez-axis direction, which is sufficient to avoid false interactions.The topological properties are calculated by the Wannier function method in the WANNIER90 package.[58,59]
3.Results and discussion
3.1.Pristine CoBr2 and Gr/CoBr2 heterostructure
The monolayer CoBr2is exfoliated from bulk CoBr2crystals, having a CdI2-type layered structure, as shown in Figs.1(a) and 1(b), in which a cobalt metal atom forms an octahedron with six bromine atoms.[60]The adjacent layers of monolayer CoBr2are stacked together by weak vdW force, like in graphene, but it is reported to be stable in mechanics and thermodynamics.[48,49]The structure showsP¯3m1 (No.164) symmetry with broken inversion symmetry.The lattice parameters of monolayer CoBr2are calculated to bea=b= 3.80 ˚A, and the band structure of the material[Fig.1(c)] indicates that CoBr2is a semiconductor with a global large band gap of 2.80 eV,which agrees well with previous research.[49]

Fig.1.(a)Top and(b)side views of the CoBr2 monolayer.The primitive cell is marked by the dashed lines in (a).The blue and red balls represent Co and Br atoms, respectively.(c) Band structures of the CoBr2 monolayer,Eg represents the band gap.
Considering that both CoBr2and graphene are vdW crystals, they can easily combine with each other.Here, the 3×3×1 supercell of CoBr2is chosen as the substrate for the 5×5×1 graphene for constructing a vdW heterostructure where graphene is stacked over the CoBr2.[61–66]In Gr/CoBr2,the interfacial Br atoms and the one on the other side are labeled by Br2 and Br1, respectively [Fig.2(e)].Since the interlayer interaction can be dependent on different stackings,we consider four high-symmetry configurations of Gr/CoBr2in Figs.2(a)–2(d).In A1, the Co atom is on the hollow site of the C atom.In A2, the C atom is simply on top of the Co atom.In A3, the C atom is on top of the Br2 atom and, in A4, the C atom is on top of the Br1 atom.Our calculations find that A1 has the lowest energy and we focused on A1 in this study.The top and side views of A1 are shown in Fig.2(a).The optimized lattice constant of Gr/CoBr2is 12.29 ˚A and interlayer binding energy is given byEb=[E(Gr/CoBr2)-E(CoBr2)-E(graphene)]/a2.The distance between the two layers is 3.51 ˚A, with an interlayer binding energy ofEb=-69.49 meV/˚A2, where the interlayer distance suggests that the primary mode of interaction between the monolayers of graphene and CoBr2is a weak vdW force similar to other vdW heterostructures.Considering that the heterostructure is formed by stretching CoBr2in experiments,we simulate the impact on monolayer CoBr2of an external force during heterostructure formation and compute the phonon spectrum of the monolayer CoBr2under the 7.6%strain.In Fig.S1,the phonon spectrum of the 5×5×1 supercell CoBr2has no imaginary frequency, which demonstrates that the CoBr2in the heterostructure is stable.
Next,in order to test the impact of theUvalue,we calculate the lattice constants and magnetic moments of each atom under differentUvalues, as shown in Table 1.The results show that the lattice constants change slightly when theUvalue is varied from 2 eV to 5 eV.Moreover, in Fig.S2(a),we calculate the ground state based on a 2×1×1 supercell of Gr/CoBr2according to the literature.[67]The FM and antiferromagnetic(AFM)energies(Figs.S2(b)and S2(c))are calculated to identify the ground state of the Gr/CoBr2heterostructures.It is shown that the energy of the FM configuration is lower than that of the AFM configuration whenU= 5 eV,∆E=EAFM-EFM=29.2 meV, which shows that Gr/CoBr2presents an FM ground state in the same way as CoBr2.
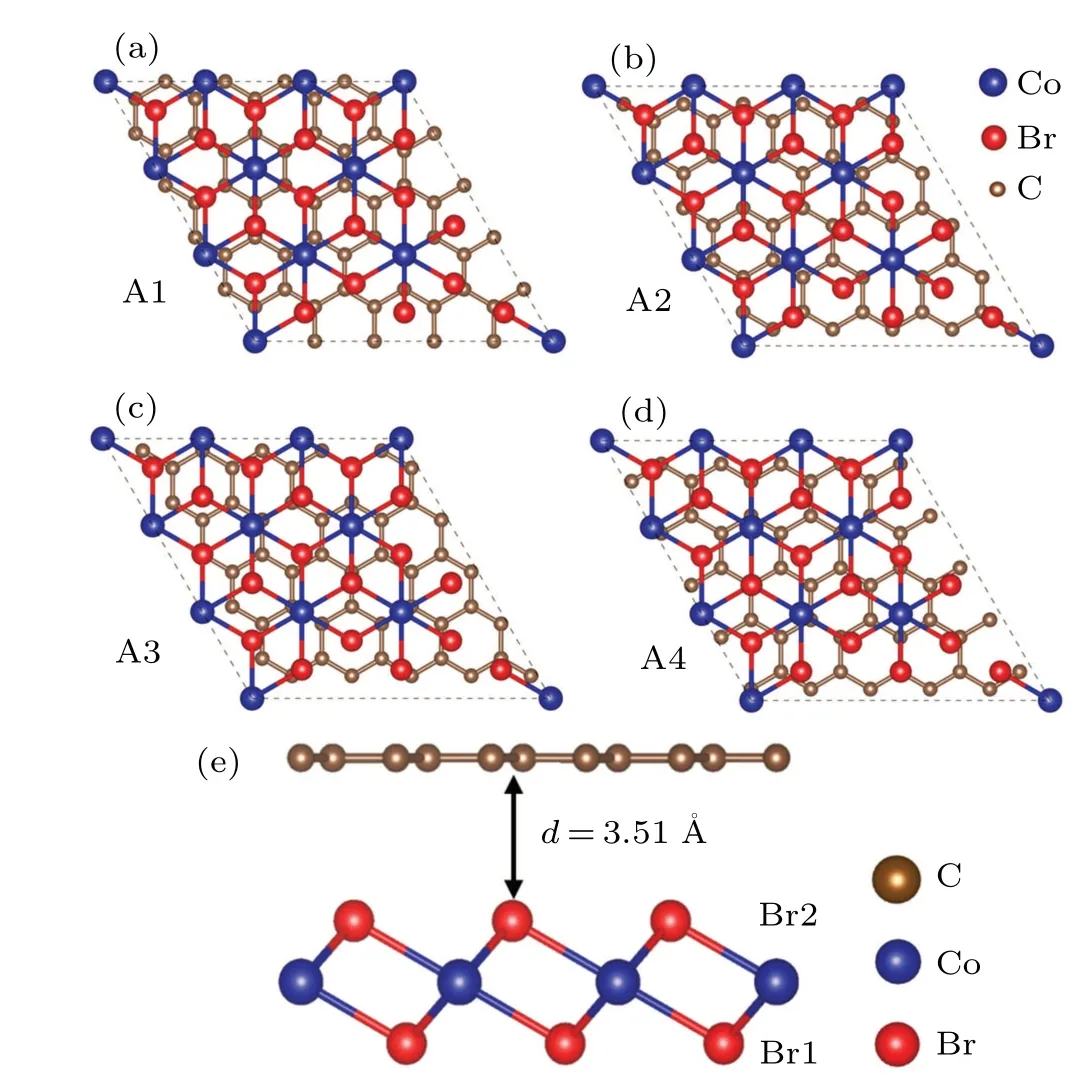
Fig.2.(a)–(d)The top view of Gr/CoBr2 heterostructures with A1,A2,A3 and A4 stackings.The brown spheres represent C atoms.(e) The side view of Gr/CoBr2 heterostructure with A1 stackings.

Table 1.The lattice constants a, magnetic moments of Co mCo, Br1 mBr1,Br2 mBr2 and C mc under different U values.
3.2.Magnetic anisotropy tuned by interlayer spacing
CoBr2is a member of the 2DXYmagnet family, i.e.,it has an easy magnetic axis in the in-plane direction.Our calculation shows that the energy of the CoBr2monolayer is lowest when the electron spins along the in-plane direction, ∆EMAE=Ex-Ez=-0.85 meV, which accords with the above conclusion.The MAE of Gr/CoBr2when the easy magnetization axis is along the in-plane direction is shown in Fig.S3.Similarly, we investigate the MAE of 2D Gr/CoBr2when the SOC is included.In Gr/CoBr2,we can calculate that∆EMAE=-8.17 meV.The calculated result shows a preferred in-plane magnetization that is much larger than that of the monolayer CoBr2.It is clear that the construction of Gr/CoBr2achieves the increase of MAE,providing a promising avenue for the development of spintronic devices.


Fig.3.The layer-resolved MAE of Gr/CoBr2 with ∆d=0.0 ˚A,-0.2 ˚A,-0.4 ˚A,-0.6 ˚A,-0.8 ˚A and-1.0 ˚A,respectively.
After constructing Gr/CoBr2heterostructures, the attenuation of Co-〈dx2-y2|Lx|dxy〉 and the enhancement of Co-〈dyz|Lx|dxz〉 increase the IMA in Fig.4(b).Similarly, in Gr/CoBr2,we find that the IMA of Co atoms increases significantly with the decrease of interlayer distance, which causes the IMA increase of Gr/CoBr2.Moreover,when the interlayer distance between graphene and CoBr2decreases by 1 ˚A, the weakening of the orbital hybridization between Co-dxyand Co-dx2-y2causes the IMA of Gr/CoBr2to increase remarkably, as shown in Fig.4(c).In 2D materials, MAE can stabilize long-range FM order, withstanding the impact of thermal fluctuations.Naturally,MAE includes magnetocrystalline anisotropy (MCA) energy and magnetic shape anisotropy(MSA) energy, i.e.,EMAE=EMCA+EMSA.[68]MSA is not considered in spin-density-based first-principles calculations.The MCA energy is related to the energy difference between the magnetization between the in-plane and out-of-plane direction relative to the CoBr2layer,∆EMCA=ESOCx-ESOCz.



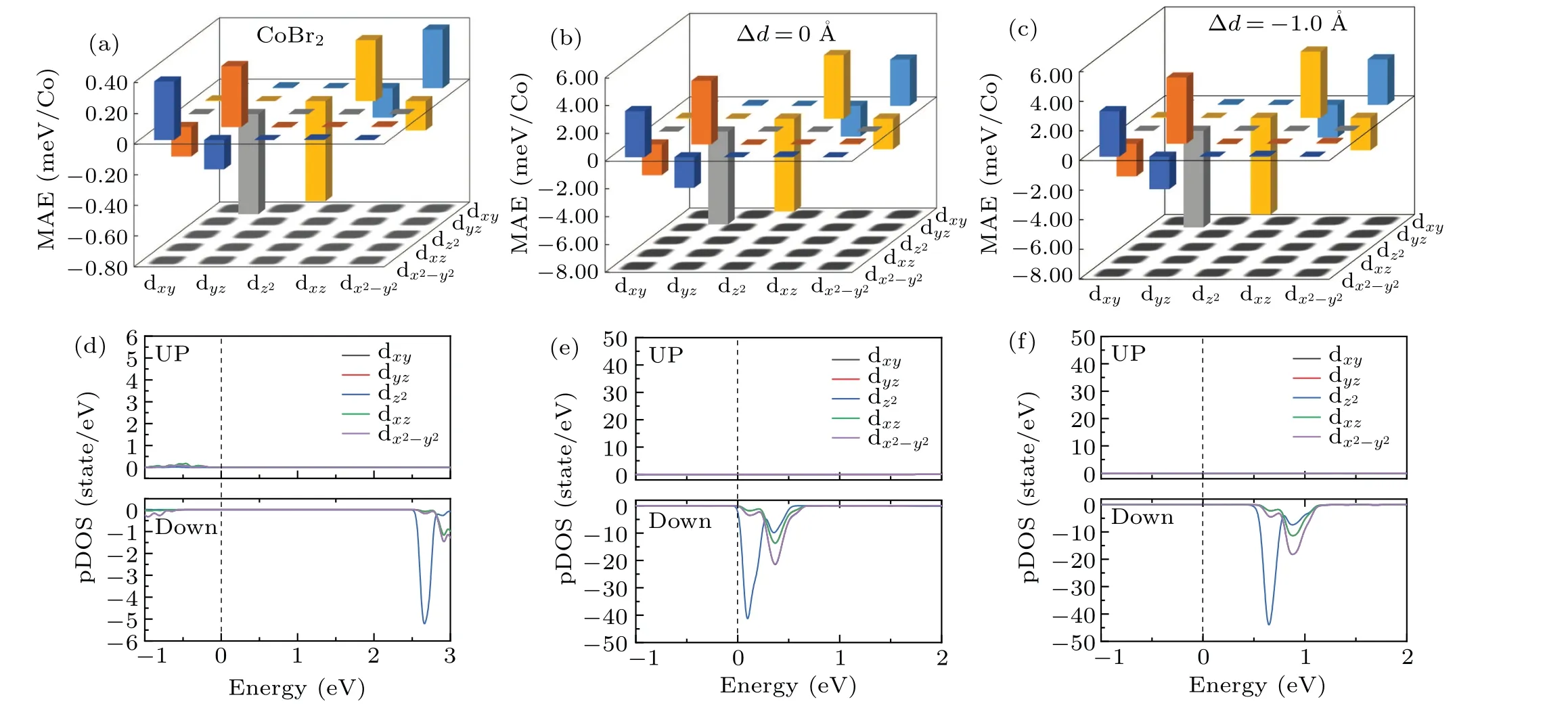
Fig.4.MAE contributions from d-orbital hybridization of Co atoms in (a) pristine CoBr2, Gr/CoBr2 heterostructure with (b) ∆d =0.0 ˚A, (c) ∆d =-1.0 ˚A.The pDOS of Co atom in(d)pristine CoBr2,Gr/CoBr2 heterostructure with(e)∆d=0 ˚A,(f)∆d=-1.0 ˚A.
Our results of the MAE also show that the Gr/CoBr2heterostructures belong to the 2DXYmagnet family.For 2DXYmagnets, the finite size effect can be used to steady its magnetic order.In addition, the results show that the stability of the FM order in 2DXYmagnets is strongly correlated with MAE.In order to demonstrate the effect of MAE on the magnetic transition temperature, we further determine the critical temperatureTKT.[73]According to the classicalXYmodel,we estimate the critical temperature

Here,Sandzrepresent the spin of the Co atom and the number of nearest-neighboring Co atoms,respectively.
Considering only the first-nearest interactions,we obtain the nearest exchange integralJ1=1.31 meV and theTKTis estimated to be 23.8 K.TheTKTof the CoBr2monolayer is calculated as 1.35 K,which is close to the previously reported value (1.7 K).[49]We discover that the transition temperature of the Gr/CoBr2is 17 times higher than that of the CoBr2monolayer.Therefore, the construction of the Gr/CoBr2heterostructure not only enhances the IMA of CoBr2, but also effectively increases its critical temperature, which provides a theoretical basis for its development and application in the future.

Table 2.The matrix element differences of Co-d orbitals between two directions of the magnetization(z[001]and x[100])in Eqs.(2)and(3).
3.3.Electronic properties and band structure of Gr/CoBr2
In Fig.5,we present the electronic band structures in the Gr/CoBr2heterostructure with an equilibrium interlayer distance of 3.51 ˚A.Figure 5(a) shows the representative electronic band structures without SOC of Gr/CoBr2withU=5 eV,which indicates that the system is metallic and the Dirac cones of graphene are well preserved.When the SOC is considered, as shown in Figs.5(b) and 5(c), we discover that the energy band opens up to a very small band gap (Eg=6.25 meV).
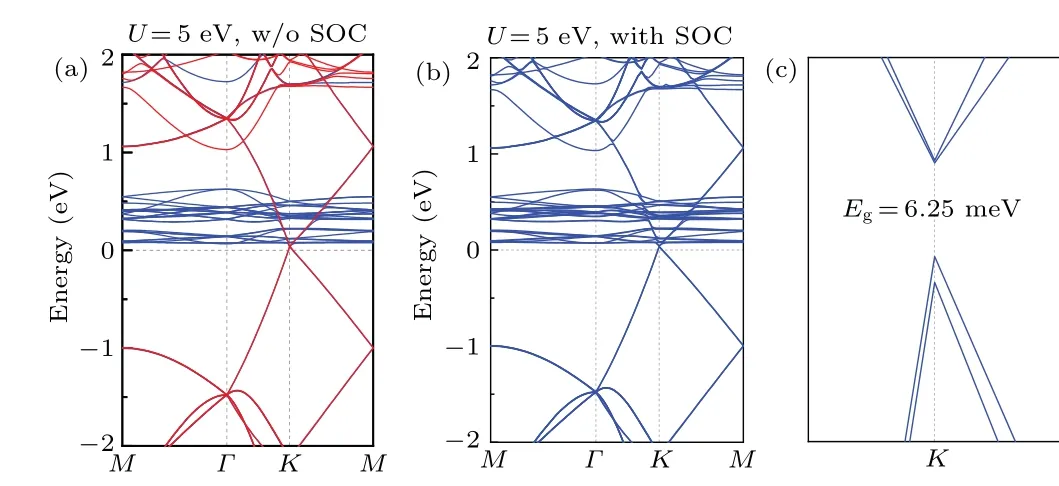
Fig.5.(a)The energy band structures for the Gr/CoBr2 heterostructure,with U values of 5 eV without considering the SOC.The red and blue lines represent spin-up and spin-down states, respectively.(b)Considering the SOC,the band structures with U values of 5 eV(c)Enlarged view of the band gap near the Fermi surface in(b).
Furthermore, in vdW heterostructures, it is proved that decreasing the interlayer distance can effectively tune the Dirac cones of graphene; hence, here we plot the band structure when the interlayer distance decreases by 0.2 ˚A to 1.0 ˚A,as shown in Figs.6(a)–6(e).With decreasing interlayer distance, the opposite spin states are separated effectively by a strong magnetic exchange interaction,which produces significant exchange splitting when the interlayer distance is reduced to 2.51 ˚A, as shown in Figs.6(e) and 6(f).Therefore, we chooseU=5 eV,d=2.51 ˚A for the subsequent calculation of SOC in order to distinctly show the topological properties of Gr/CoBr2.

Fig.6.(a)–(e)In the Gr/CoBr2 heterostructure,the energy band structures with ∆d=-0.2 ˚A,-0.4 ˚A,-0.6 ˚A,-0.8 ˚A and-1.0 ˚A,respectively.(f)Enlarged view of the black circle in(e).
3.4.Topological properties of the Gr/CoBr2 heterostructure
A global band gap of∼14.3 meV opens after SOC is switched on, where theEFis right tuned to lie inside the global gap,as shown in Figs.7(a)and 7(b),indicating that the Gr/CoBr2heterostructure may harbor topologically nontrivial states.
Firstly, in order to analyse the cause of the QAHE, the theoretical model proposed by Renet al.is employed in Gr/CoBr2.[74]The tight-binding Hamiltonian with in-plane magnetization can be written as
For Gr/CoBr2, the broken symmetries ofT ⊗Mz ⊗I(inversionI,time reversalT,out-of-plane mirror reflectionMz) andT ⊗Mzin 2D systems allow nonzero Chern numbers to occur,as expressed in references.[74–76]The emergence of magnetic substrates such as CoBr2and the construction of a supercell provide a possible pathway for the realization of the QAHE by decreasing the nearest-neighbor hopping energy.Onceλ>t, the degeneracy is lifted, the band gap opens and the QAHE is characterized by Chern numbers ofC=1,which is consistent with the model.
To determine whether or not the resulting insulating state exhibits nontrivial topological properties, we evaluate the intrinsic anomalous Hall conductivityσ,
whereeandhare the elementary charge and the Planck constant,respectively,the Berry curvatureΩ(k)summed over occupied valence bands can be expressed by
Herefnis the Fermi–Dirac distribution function,vxandvyare the velocity operators, andEnis the eigenvalue of the Bloch function|ψnk〉.
Figure 8(a) shows the anomalous Hall conductivityσxy.We can see thatσxyis quantized (e2/h) as expected when the band gap of Gr/CoBr2contains a Fermi level.The result means the Chern numberC=1, which also can be obtained by the formula
Theσxyrapidly reaches 0 as the Fermi level moves away from the band gap.Furthermore, the topological property of Gr/CoBr2is also estimated by the hybrid Wannier charge centers (WCCs) in Fig.8(b).The electronic polarization WCC shifts with the winding number 1, which confirms the Chern number.Thus, it can be concluded that the Gr/CoBr2heterostructure harbors topologically nontrivial properties.
Notably,the QAHE can be achieved by changing the interlayer distance.Based on this, we propose a conceptual topological field-effect transistor that operates by switching the topological behavior of the Gr/CoBr2heterostructure on and off, as shown in Fig.9.When the interlayer distance decreases by 1.0 ˚A,the device is in an‘on’state and the current will flow without dissipation in the edge states.In contrast,if the interlayer distance is not compressed,the device could be turned‘off’because of the lack of conductive channels.This study provides a new idea for the development of new spintronic devices with low-power consumption.
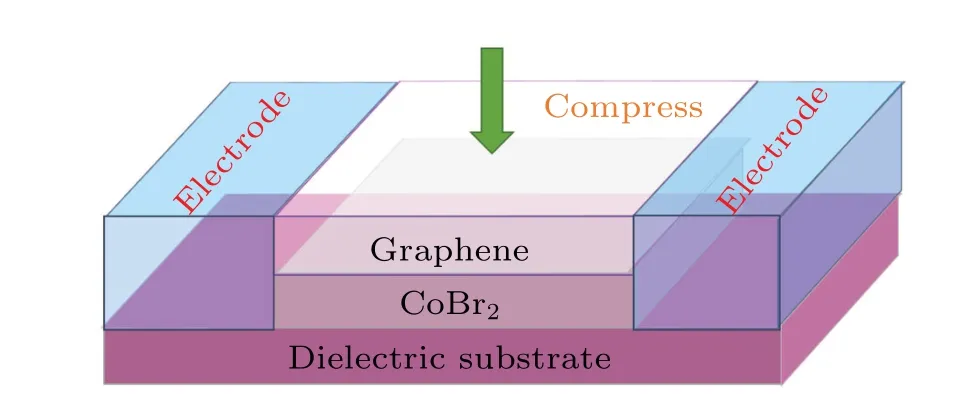
Fig.9.Schematic diagram of the topological field transistor model.
4.Conclusion
In summary, we construct a Gr/CoBr2vdW heterostructure and predict its magnetic anisotropy and topological properties by first-principles calculations.The conclusion reveals that the Gr/CoBr2heterostructure is an FM semiconductor with IMA,belonging to the 2DXYmagnet family withTKT=23.8 K.The MAE can be enhanced by decreasing the interlayer distance.However, the cause of MAE variation is the attenuation of Co-〈dx2-y2|Lx|dxy〉and the enhancement of Co-〈dyz|Lx|dxz〉.The second-order perturbation theory shows that graphene can tune the electronic states of Co atoms, thereby enhancing the MAE arising by hybridization.Moreover, by analyzing the band structure, we elucidate that the decrease of interlayer distance produces a large exchange splitting in Gr/CoBr2.After considering SOC,a global band gap of about 14.3 meV appears.Furthermore, anomalous Hall conductivity, a nonzero Chern number (C=-1) and WCC prove the topologically nontrivial property of Gr/CoBr2.Our findings demonstrate that adjusting the vdW layer distance can not only control the MAE of 2D FM materials,but also provide a new way to realize the QAHE.Finally, on this basis, we design a topological field-effect transistor model,which provides a new idea for the development of new low-power spintronic devices.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.52173283), Taishan Scholar Program of Shandong Province(Grant No.ts20190939), and Independent Cultivation Program of Innovation Team of Jinan City(Grant No.2021GXRC043).
- Chinese Physics B的其它文章
- Unconventional photon blockade in the two-photon Jaynes–Cummings model with two-frequency cavity drivings and atom driving
- Effective dynamics for a spin-1/2 particle constrained to a curved layer with inhomogeneous thickness
- Genuine entanglement under squeezed generalized amplitude damping channels with memory
- Quantum algorithm for minimum dominating set problem with circuit design
- Protected simultaneous quantum remote state preparation scheme by weak and reversal measurements in noisy environments
- Gray code based gradient-free optimization algorithm for parameterized quantum circuit

