Simulation of optimal work extraction for quantum systems with work storage
Peng-Fei Song(宋鹏飞) and Dan-Bo Zhang(张旦波),2,†
1Key Laboratory of Atomic and Subatomic Structure and Quantum Control(Ministry of Education),and School of Physics,South China Normal University,Guangzhou 510006,China
2Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,Guangdong–Hong Kong Joint Laboratory of Quantum Matter,and Frontier Research Institute for Physics,South China Normal University,Guangzhou 510006,China
Keywords: quantum algorithm,quantum thermodyanmics
1.Introduction
Work extraction from heat engineers plays a central role in thermodynamics due to its practical and fundamental importance.[1–4]For quantum systems,identifying how different types of quantum resources,e.g.,entanglement,coherent,or squeezing, can affect the work extraction has drawn much attention.[5–12]Moreover,work extraction can be exploited for formulating quantum thermodynamics as well as for characterizing symmetry-protected thermal equilibrium.[13]Apart from those theoretical interests, recent quantum technology advances have also enabled us to build quantum heat engines and explore quantum thermodynamics on various quantum platforms such as trapped ions and superconducting qubits.[14–17]
For different setups, investigating the amount of extractable work as well as the protocol of realization can be important as it is operational.[18–20]In a prototypical scenario,the work can be extracted from a quantum system by a cyclic unitary evolution.[21]The maximal extractable work, called ergotropy,[3]may be realized by optimizing the cyclic unitary evolution.Another scenario includes a work storage and the unitary operator should be performed on the composite system for transferring the energy from the system to the work storage.[22,23]For generic quantum systems, determining the optimal extractable work as well as constructing the associated cyclic unitary operator are in general hard as they demand optimization in an exponentially growth space.Such difficulty is intrinsic to quantum systems of many degrees of freedom.[24–26]
On the other hand,with advances both in quantum hardware and quantum algorithms, quantum computing has been widely exploited for simulating both static and dynamic properties of quantum systems.[27]For instance,the thermodynamics of quantum systems can be investigated by preparing equilibrium thermal states at finite temperatures and measuring the observables.[28]While recent protocols for optimal work extraction often concern systems with a few degrees of freedom,the current advances have enabled us to simulate work extraction for larger quantum systems.[29–31]
In this paper,we propose a variational quantum computing approach for simulating optimal work extraction for quantum systems with a work storage.[32–35]With a unitary transformation, energy can be transferred from the system to the work storage.We enforce energy conservation in work extraction and consider energy conservation both strictly and on average.We give constructions of unitaries satisfying strict and average energy conservation respectively, and formulate their corresponding variaitonal quantum algorithms.By numeral simulation with a fully connected quantum Ising model,we demonstrate the variational quantum computing approach for the work extraction and compare results for the strict and average energy conservation.
The paper is organized as follows.In Section 2,we introduce the concept of maximum extractable work and its evaluation with a variational quantum algorithm.In Section 3, we discuss the work extraction with work storage under two different scenarios and propose their simulations with a hybridvariable quantum circuit.The simulation results are presented in Section 4.Finally,we give conclusions in Section 5.
2.Maximum extractable work
In this section, we briefly review the maximum extractable work for a quantum system and propose a variational quantum algorithm for evaluating the maximum extractable work.[3,21]
How much work can be extracted from a heat engine is not only of practical value but also lies at the heart of formulating the second law of thermodynamics.Investigation of work extraction has also been generalized for quantum heat engines under different circumstances in recent years.[36–38]Here we restrict our discussion to a prototypical scenario, where work extraction is achieved by performing a cyclic unitary evolution on an isolated quantum systemS(see Fig.1).The maximum extractable work in this scenario is quantified as ergotropyWE.It is possible to generalize the setup to a more realistic process of work extractable by letting the system contact the heat bath.[39]
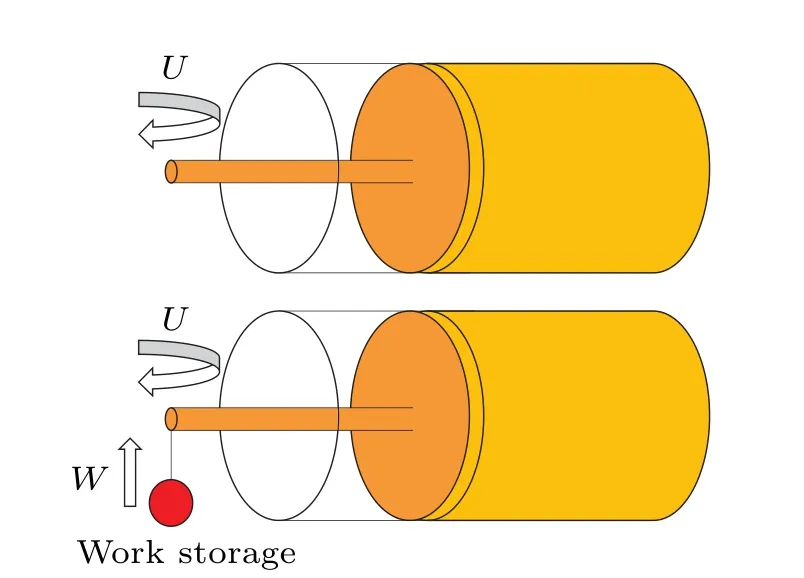
Fig.1.Illustration of work extraction for quantum systems after a cyclic unitary evolution without(up)and with work storage(bottom).Without work storage,the energy is extracted as much work as possible from the system by a cyclic unitary evolution U.When there is work storage,the extracted energy can be used for work,e.g.,lifting a weight.
There are two situations here.When there is no work storage, work extraction is just to extract as much energy as possible from a system through some unitary evolution.However, the goal of extracted work in practice should be of utility.In this case,one can introduce work storage in which the extracted energy is utilized, for instance, for lifting a weight.The work storage can also refer to a battery that can store the extracted energy for later usage.
We first formulate the work extraction and the ergotropy[40,41]by considering a quantum system described by the HamiltonianHand initialized in a quantum state denoted by a density matrix,ρs(t=0)=ρs0.By manipulating the cyclic varying external fieldV(t) in a periodτ, the quantum system evolves under a time-dependent Hamiltonian,H(t)=H+V(t),where the time-dependentV(t)accounts for a transfer of work during the evolution.In a single cyclic process, the systemSis coupled to an external field in a period 0≤t ≤τ,and decouple att>τ.The density matrix at timetfollows the Schrödinger equation

where〈ψi|ψj〉 =δij,Ekand|Ek〉 are the eigenvalues and eigenstates of the Hamiltonian, respectively.Here we have sorted all probability densities ofρsin descending order and eigenvalues of the system Hamiltonian in ascending order.
It is important to note that a unitary transformation onρs0will not change the probability distribution{pi}.Then it can be verified that the final state for the ergotropy should be a mixture of pure states{|Ej〉}with a higher probability for a lower-energy state|Ej〉.In this regard, the final state can be expressed as

The task is to find a cyclic unitary transformation that the maximum work or the ergotropyWEcan be extracted.From above it can be deduced that such a unitary operator for maximal work extraction can be written as
It can be verified thatU†U=∑j|ψj〉〈ψj|=1.
WhileUin Eq.(6) can be explicitly given, it requires diagonalizing both the initial stateρs0and the HamiltonianH.For a generic many-body quantum system, the value of ergotropy as well as the corresponding unitary transformation for extracting the maximum work are not easy to obtain,as can be argued by the curse of exponential growth of Hilbert space with the system size for diagonalization.Such a challenge can be solved by quantum computing.Since the goal is to maximize the extracted energy,it is suitable to exploit a variational quantum computing approach, where the desired unitary operatorUcan be optimized by maximizing the energy reduced for the system.It should be stressed that the optimizedUis specified for a given initial stateρs0and may not be the same as the one in Eq.(6)which is general for all initial states given in Eq.(3).
As it is essential to find a unitary operator in the final state that the lowest energy, we can consider it as an optimization problem and exploit a variational quantum algorithm to find an optimal unitary operator.It should be emphasized that the unitary operator is parameterized by the cyclic evolution of time-dependent HamiltonianH(t), which may be limited by the degree of control HamiltonianV(t).As a consequence,the optimal extractable work may be smaller than the ergotropy.In this work,we assume that the system is highly controllable and can be used to generate arbitrary unitary operators.Thus,we relax the condition of cyclic unitary evolution to a unitary operator generated by a quantum circuit composed of sequences of quantum gates.The unitary operator represented the quantum circuit should be generated with a cyclic evolution of time-dependent Hamiltonian as both can be universal for quantum computing.In other words, we exploit a digital quantum computing approach for simulating work extraction in quantum systems, leaving an analog quantum simulation with more realistic cyclic Hamiltonian evolution for future investigation.
Now we propose a variational quantum algorithm for evaluating the ergotropy.For a parameterized quantum circuitU(θ), the final state evolved fromρs0byU(θ) can be expressed as,ρs(θ)=U(θ)ρs0U†(θ).The variational energy for the final state is
The variational energy can be set as the cost function and should be minimized by finding the optimized parameter setθ*, which can refer to a hybrid quantum–classical optimization procedure.The variational quantum algorithm is closely related to the subspace-search variational quantum eigensolver(SS-VQE),[42,43]whose cost function is a weighted linear combination of variational energies with a set of orthogonal initial state and the same parameterized unitary operator.Alternatively, one can view that the cost function of SS-VQE takes the form of Eq.(7).Ideally,the unitary operatorU(θ*)should transform each|ψj〉into thek-th lowest-energy eigenstate of the system Hamiltonian,and thus the extracted energy is equal to the ergotropy.The variational quantum algorithm can obtain an approximate ergotropy, which depends both on the expressivity of the ansatzU(θ)as well as the optimization.In Algorithm 1,we present the algorithm.

Algorithm 1:U(θ*)Input: Parameter θ to be optimized, system Hamiltonian H,initial state ρs.Output:U(θ*)1 Construct a quantum circuit U(θ)with reference;2 Apply U(θ) to the initial state ρs of the system, then obtain ρs(θ)=U(θ)ρsU†(θ);3 The system energy can be expressed as E=Tr(ρs(θ)H);4 The gradient descent algorithm is used to minimize system energy E;5 When E reaches the minimum value, the optimization stops and the optimization parameter θ* is obtained;6 Bring θ* back to U(θ)to get U(θ*)for the final desired solution.
The obtainedU(θ*)has some capacity for generalization.For any density matrix composed of a mixture of pure states as follows:

3.Work extraction with work storage
Previously,we proposed a variational quantum algorithm for maximal work extraction where the quantum system is not coupled to work storage.In practice, however, work should be output and the work storage is necessary.In this section,we investigate work extraction with the work storage.Following Ref.[1], the work storage is chosen to be described by a continuous variable for two reasons.First, a continuous variable can be used for simulating a process of doing work such as lifting a weight.Second, the continuous variable allows for non-deterministic work extraction(to be explained later in Eq.(2)).As a comparison, a qubit work storage with HamiltonianHw=gZcan only allow for deterministic work extraction.We consider a system of qubits.[20,44–46]In this regard,the whole system consists of both discrete-variable qubits and one continuous-variable, and it is conventional to simulate it with a hybrid-variable quantum circuit.[1,47–49]
With a work storage, the energy can be transferred from the system to the work storage, and therefore energy conservation can be considered in this setup.We investigate energy conservation in two scenarios.The first is restriction which requires that energy conservation should be respected in the process of work extraction.[20,45]In other words, the unitary transformation should commute with the Hamiltonian of the whole system.The second relaxes the condition and requires energy conservation on average.[1]For both scenarios,we propose variational quantum algorithms for optimal work extraction.
We use a simple example to tell the difference between strict energy conservation and average energy conservation.The Hamiltonian of the two systems isHA=ZAandHB=ZB,and the total HamiltonianH=ZA+ZB.Considering the evolutionary operatorU= e-iZAZBtwhich always satisfies the commutation with the total Hamiltonian.Then the total energy is always conserved,regardless of the initial state chosen.On the other hand,if one chooses the evolution operatorUasU=XAXB, thenUdoes not satisfy the commutation relation with the total HamiltonianH.The total energy is still conserved for an initial state|01〉or|10〉but is changed for other initial states such as|00〉 or|11〉.In this regard, energy conservation is kept on average for some given states and one can call it as average energy conservation.
3.1.Strict energy conservation
We first investigate the situation in which the unitary operator commutes with the total Hamiltonian.[13,49]The Hamiltonian of the work storage can be expressed in terms of the position operatorx.We assume that the coupling between the system and the working storage only exists in the process of extracting and transferring energy by implementing a unitary operator on the composite system.Before and after the unitary operation, the interaction between the system and the work storage can be ignorable.Then, the total Hamiltonian of the system and work storage can be expressed as follows:
Now we aim to construct the desired unitary operatorCU.Two conditions need to be satisfied forCUduring the process of transferring work:(i)Energy conservation must be ensured,meaning that the energy lost by the system must be equal to the energy gained by the working storage,even if not all of the extracted work is transferred to the working storage.i.e.,
(ii) The energy transfer should not depend on the initial state of the work storage.That is,CUshould be invariant under energy shifts of the work storage:
wherepis the momentum operator of the work storage.
Following Kitaev construction,[50]the unitary operatorCUsatisfying the above two conditions(i)and(ii)can be written as follows:
This unitary operator is equivalent to the unitary operator found in Refs.[13,44].TheCUacts on the composite system and couples the system with the work storage with the operator e-ipH.This is an evolution of HamiltonianpHwhich involves both discrete variable qubits and continuous variables,which can be decomposed into a set of quantum gates involving a hybrid-variable quantum gate,[48,51]e.g., e-iθ pZ(Zis Pauli matrix).Such a hybrid-variable gate can be engineered on the mainstream quantum platforms.An illustrative quantum circuit forCUis shown in Fig.2.
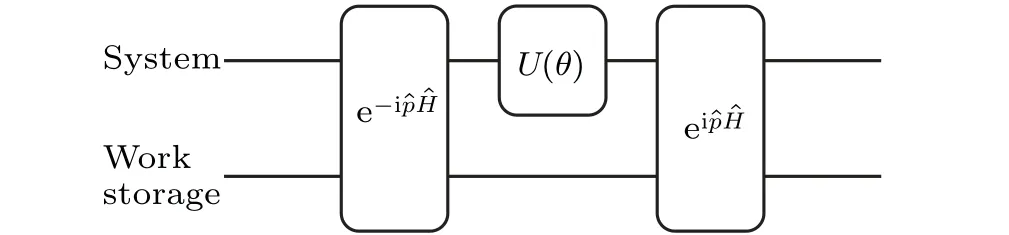
Fig.2.Quantum circuit for CU which commutes with the Hamiltonian of the composite system.The unitary operator U(θ)is constructed by a parameterized quantum circuit and the optimal θ should be obtained by minimizing the transferred energy to the work storage.
We suppose that initially the system and the work storage are uncorrelated.The transferred work can be expressed as an energy increase for the work storage before and after the operation ofCU:
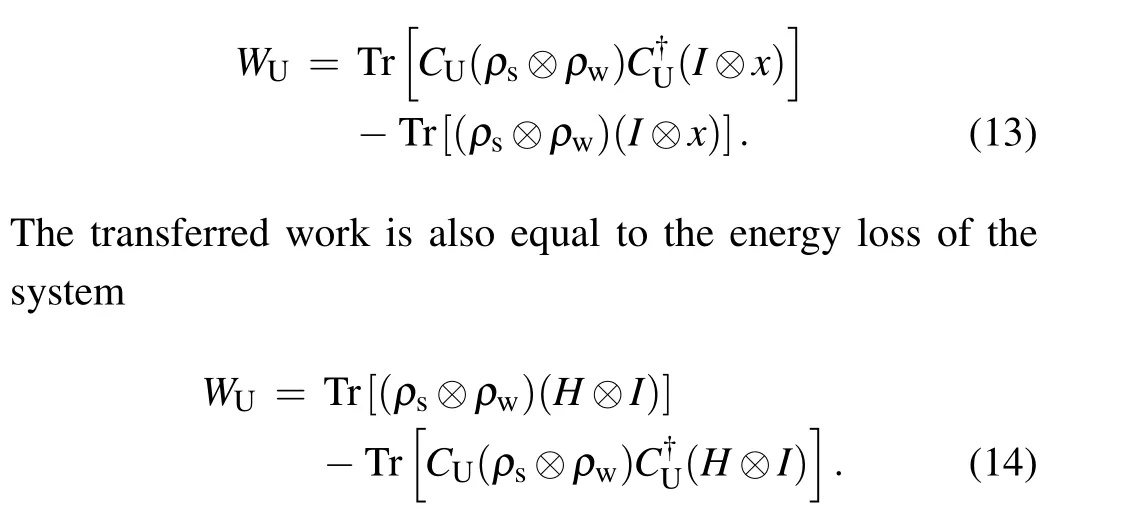
In this regard, the transferred work is equal to the extracted work.We use the transferred work preferably in the presence of work storage.
The transferred work is a function of the unitary operatorUperforming on the system.What is the optimalUthat maximizes the extracted workWU? It is tempting to insert theU(θ*)that can get the ergotropy without the work storage as in Section 3.One may expect that the same ergotropy can be obtained with the work storage.However,such a scheme fails.The reason is that there will be correlation energy between the system and the work storage after performingU(θ*)on a generic initial state.Instead,the optimalUshould be obtained by maximizing the extracted workWU.For a given initial state,this is equal to the task of minimizing the energy of the final state,
We adopt a VQA similar to one for work extraction without the work storage.With a parameterized quantum circuitU(θ),we can obtain theEU(˜θ*)by finding the optimal parameter set ˜θ*with a hybrid quantum–classical optimization procedure.The coupling of the system and the work storage makes the computation harder.However,since the coupling is fixed,the optimization only evolves the system whereU(θ) performs.In Algorithm 2, the corresponding variational quantum algorithm is outlined.

Algorithm 2:CU(θ*)Input: Parameter θ to be optimized, system Hamiltonian H,initial state of the system ρs, initial state of the work storage ρw.Output:CU(θ*)1.Construct a parameterized quantum circuit CU(θ)for the system and work storage as a whole;2.Apply CU(θ) to the initial state ρs ⊗ρw of the system and work storage as a whole, the result is represented by ρ(θ)=CU(θ)ρs ⊗ρwC†U(θ);3.Use gradient descent algorithm to minimize the final energy E=Tr[ρ(θ)(H ⊗I)]of the system;4.Stop the optimization when E reaches the minimum value,and obtain the optimized parameter θ*;5.Inserting θ* into CU(θ) gives the evolution operator CU(θ*)for the entire system and work storage.
The advantage of this approach is that it is operationally simple and does not require additional computational demands.However, the work transferred byCUfrom(ρs⊗ρw)may not be the same as the work extracted byUfromρs.Notably,the optimal transferred workW(U)typically will be smaller than the ergotropy.In the next section, we will consider a setup where the optimal transferred work can be equal to the ergotropy.
3.2.Average energy conservation
When restricting the unitary operator to be commutative with the total Hamiltonian,the optimal transferred energy will be smaller than the ergotropy.A possible way to reach the ergotropy is to relax the restriction to average energy conservation,which requires that energy is conserved before and after the unitary transformation.[44,52–54]We give an expression of the unitary operator as well as how to construct it with a variational quantum computing approach.
We suppose that the system is initially uncorrelated with the work storage.Under such a setup,the work will be maximally extracted if the energy of the system is minimized.For a density matrix as a mixture of{|ψj〉}with a descent order of weighting,p1≥p2≥···,each|ψj〉should be transformed into thej-th lowest-energy eigenstate of the system Hamiltonian, while the probabilitypjis unchanged.The energy differenceεjis
The work extracted from the system is equal to the weighted sum of the work extracted for each pure state|ψj〉, namely,WE=∑j pjεj.Each state transformation|ψj〉→|Ej〉 should be accompanied by an energy transfer ofεjto the work storage.Thus,the unitary operator may be constructed as follows:
whereΓ(ε)= eipεshifts the position of the continuous variable byεand thus the working storage gains energy ofε.By construction, the unitary operatorVwill conserve the energy but typically not commute withHsw.
As seen in Eq.(17), the construction ofVrequires a knowledge of all eigenstates ofHand usually, it is a formidable task.We consider that the initial density matrix is low-rank,e.g.,the mixture is dominated by a few components and the number of elements in the set of pure states{|ψj〉}is small.In this case,we may refer to a variational quantum computing approach in that the work can be maximally extracted and transferred to the work storage.[2]
To be more general, we suppose that the set{|ψj〉}is given but unknown.Moreover, it respects the descent ordering when forming a mixed state.As|ψj〉are orthogonal,it is possible to make a unitary transformation between the computational basis|j〉 and{|ψj〉}.The unitary operator can be parameterized asS(ϑ),which gives the following transformation:
WithS(ϑ), one then can turn each conditional shift operator|Ej〉〈ψj|⊗Γ(εj) as|j〉〈j|⊗Γ(εj) which can be implementable on a digital quantum computer.
We also denote a unitary transformation from|ψj〉to|Ej〉asU(θ).With bothS(ϑ) andU(θ), the unitary operator for work extraction with work storage can be expressed as (also see Fig.3 for the quantum circuit).In this way,AUcan be expressed as
WithS(ϑ), it is possible to decompose the conditional translation operator into|j〉〈j|⊗Γεjwhich is implementable.In the following, we give a procedure to determineAU(ϑ,θ)by dividing the task into three major subroutines: trainingS(ϑ),trainingU(θ),and evaluating{εj}.
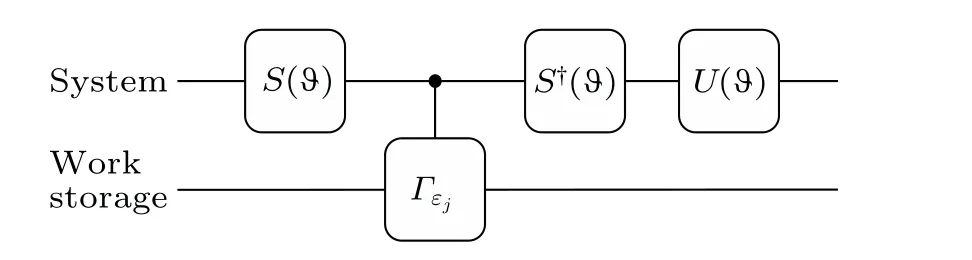
Fig.3.The quantum circuit diagram for the unitary operator AU in Eq.(19) introduces a new operator S(ϑ) to transform the initial unknown but given quantum state into a computational basis.Then, the conditional translation operator |j〉〈j|⊗Γεj is used to perform work transfer operations to ensure energy conservation, and the operator U(θ)is the same as one for maximal work extraction.
(I)TrainingS(ϑ)
The unitary operatorS(ϑ)should satisfy Eq.(18).It aims to transform the system from an unknown but given quantum state|ψj〉to the computational basis|j〉.To transform with the right ordering, we design a HamiltonianHo=∑j j|j〉〈j| and the cost function turns out to be,
The cost function reminds us of the SS-VQE.In fact, it uses SS-VQE in a reverse way.Sincep1≥p2≥···,S†(ϑ)|ψj〉=|j〉can be enforced by minimizingEo(ϑ).The algorithm for determiningS(ϑ)is outlined in Algorithm 3.

Algorithm 3: S(ϑ*)Input: Parameter ϑ to be optimized,initial state ρs Output: S(ϑ*)1.Construct a parameterized quantum circuit S(ϑ);2.Assume a system’s Hamiltonian Hm,with eigenstates|ψj〉and eigenvalues j,where j=0,1,2···;3.Apply the quantum circuit S(ϑ)to the initial state of the system to obtain ρs(ϑ)=S(ϑ)ρsS†(ϑ);4.The energy of the initial state in the system can be represented as E=Tr(ρs(ϑ)Hm).Use gradient descent algorithm to minimize E;5.Stop optimizing when E reaches its minimum value, and obtain the optimized parameter ϑ;6.Substitute ϑ into S(ϑ)to obtain the desired S(ϑ*).
(II)TrainingU(θ)and evaluating{εj}
According to the previous part of this article,U(θ) can be determined by the variational quantum algorithm in the Algorithm 1.In this regard,the optimalU(θ*)for evaluating the ergotropy can be adopted directly here.Then each transferred energyεjcan be evaluated as
It should be pointed out that the approach relies on two variational quantum algorithms and the capacity of maximal work extraction can depend on many factors, including both the ansatzes and the optimization.Notably, the energy may only be approximately conserved as the energy transformation may be affected by the accuracy ofS(ϑ).
4.Simulation results
In this section,we present simulation results for work extraction without and with the work storage.The Hamiltonian of the system is chosen as a fully-connected transverse Ising model.We first investigate the maximum extractable work in the absence of the work storage.Then, the optimal work extraction is explored with the work storage for the cases of strict and average energy conservation,respectively.
4.1.Maximum extractable work
We consider a quantum system described by the fully connected transverse Ising model,which can be written as
The coefficientsaiandJijof the Hamiltonian function are artificially chosen randomly to be close to each other,in order to prevent the coefficients of some terms from differing too much and thus the energy eigenvalues of the different eigenstates of the system from varying too much,which may make the search for minima using the gradient descent algorithm less difficult.Of course, the choice of these coefficients does not affect the final calculation results.
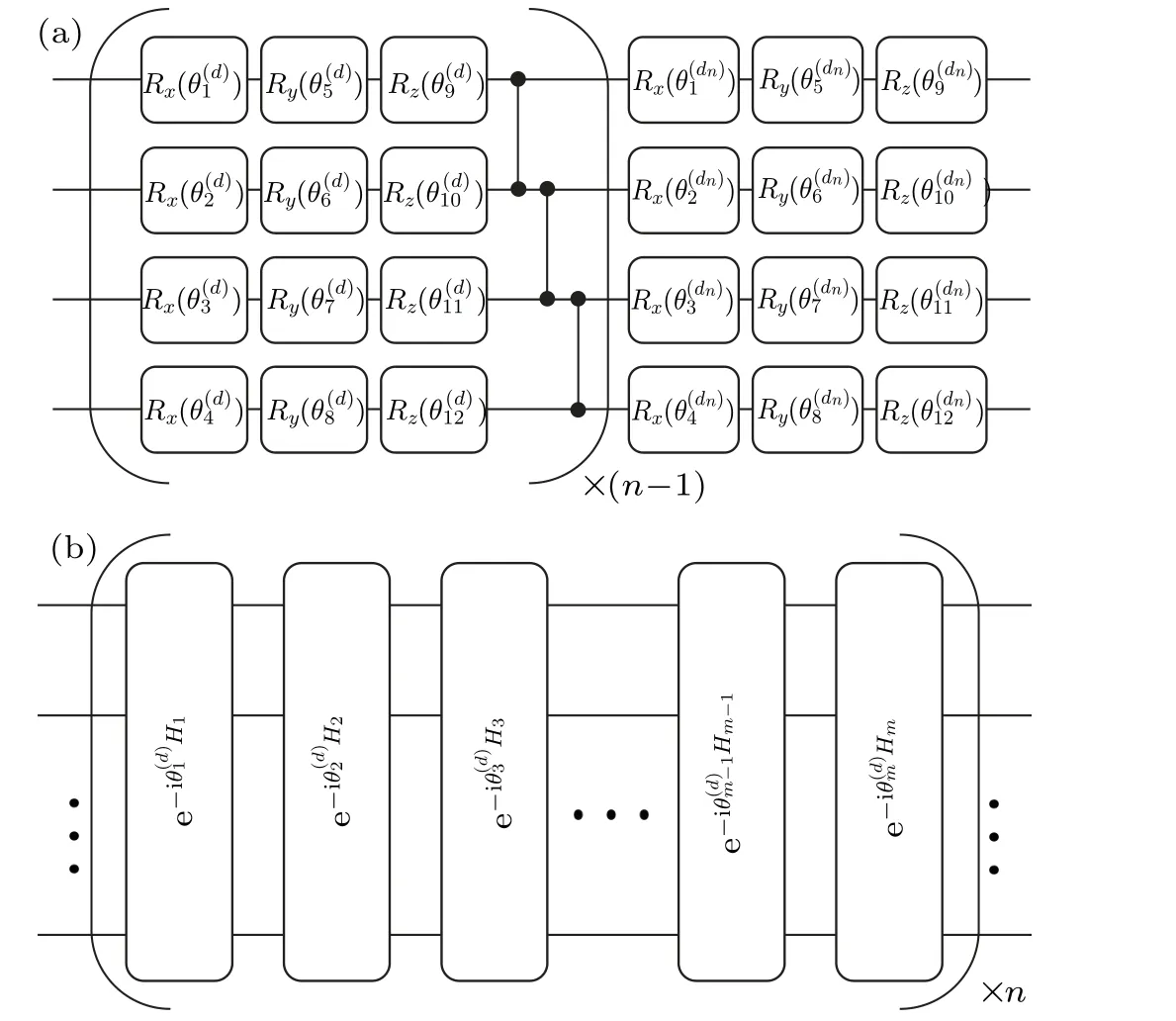
Fig.4.Quantum circuits for two ansatzes.(a)U1(θ)is the hardware-efficient ansatz;(b)U2(θ)is the Hamiltonian variational ansatz.
For variational evaluation of the ergotropy by quantum computing,a chosen ansatz is important.For this we consider two widely applied ansatzes as illustrated in Fig.4.The first one,denoted asU1(θ),is a hardware-efficient ansatz that consists lays of single-qubit rotations and two-qubit gates.[55]Fornblocks,it contains a total of 2nLparameters,whereLis the number of qubits.The second one is the Hamiltonian variational ansatz, which is physically inspired by exploiting the structure of Hamiltonian.By writingH=∑mi=1Hiwhere terms in eachHiare commutative,the unitary evolution is generated by alternating evolution ofHi.Undernlayers of a quantum circuit, it contains a total ofmnparameters, which is independent of the number of qubits.Although the ansatzU2(θ)is typically less expressive than the ansatz,it is easier to optimize and often can represent some special states, e.g., the ground state.[56,57]However,it is not known whether the ansatzU2(θ)is suitable for maximal work extraction.For the Hamiltonian in Eq.(22),we can choose
and thusm=2.
As for demonstration, the number of qubits inHsis set asN=3.To test the performances of the two ansatzes, we choose several random initial mixed quantum states.
We first set the initial state of the system to a diagonal density matrix.The density matrix of the initial state can be represented as diag[0,0.04,0.1,0.41,0,0.16,0.29,0].The diagonal elements of this matrix are the probability densities.Each probability density of the initial state is randomly selected and satisfies the condition that the total probability density adds up to 1.
Next, the initial state is set as a non-diagonal matrix.The method involves simultaneously rotating all computational basis states|j〉〈j| of the diagonal matrix by the same random angle, ensuring that these computational basis states remain orthogonal.We use a tunable rotation operator ei2π(θxiσx+θyiσy+θzσzi)and randomly select the rotation parameterθ1= (0.31,0.725,0.12),θ2= (0.59,0.13,0.126),θ3=(0.17,0.29,0.32) for three qubits.Next, the resulting operators are applied to the 2 basis vectors of each of the three quantum bits, and their results are then direct product with each other to obtain 8 mutually orthogonal computational basis vectors.Then, the probability density(0.29,0.18,0,0,0.11,0,0.42,0) of each computational basis vector is randomly selected under the condition that the probabilities sum to 1, after which they are multiplied and then summed.This gives us a randomized non-diagonal matrix initial state.We do not directly discern any useful information from the density matrix of this random initial state,including its initial eigenstate and individual probability densities.
The calculation results of the initial state as a diagonal matrix are shown in Fig.5(a).The accuracy ofU1(θ)ansatz increases with the circuit depth and finally reaches the maximum extractable work.Instead, theU2(θ)ansatz fails to get the ergotropy for an increasing circuit depth, indicating that the Hamiltonian variational ansatz is not expressive enough for maximal work extraction.The results for an initial state of a non-diagonal density matrix are shown in Fig.5(b), which also exhibit similar behaviors for two ansatzes.
In addition,we test the capacity of generalization for the optimalU1(θ*) by showing the work extraction for a class of initial states respecting the order of mixing weights.As shown in Fig.6, the sameU1(θ*) at a specified circuit depthpcan give the optimal transferred work for all initial states in the class.Moreover, theU1(θ*) can give to the maximal extractable work when the circuit depth is large enough.We should point out that the capacity of generalization is not limited to the use ofU1(θ*),while the ability to obtain the maximal extractable work is ansatz-dependent.
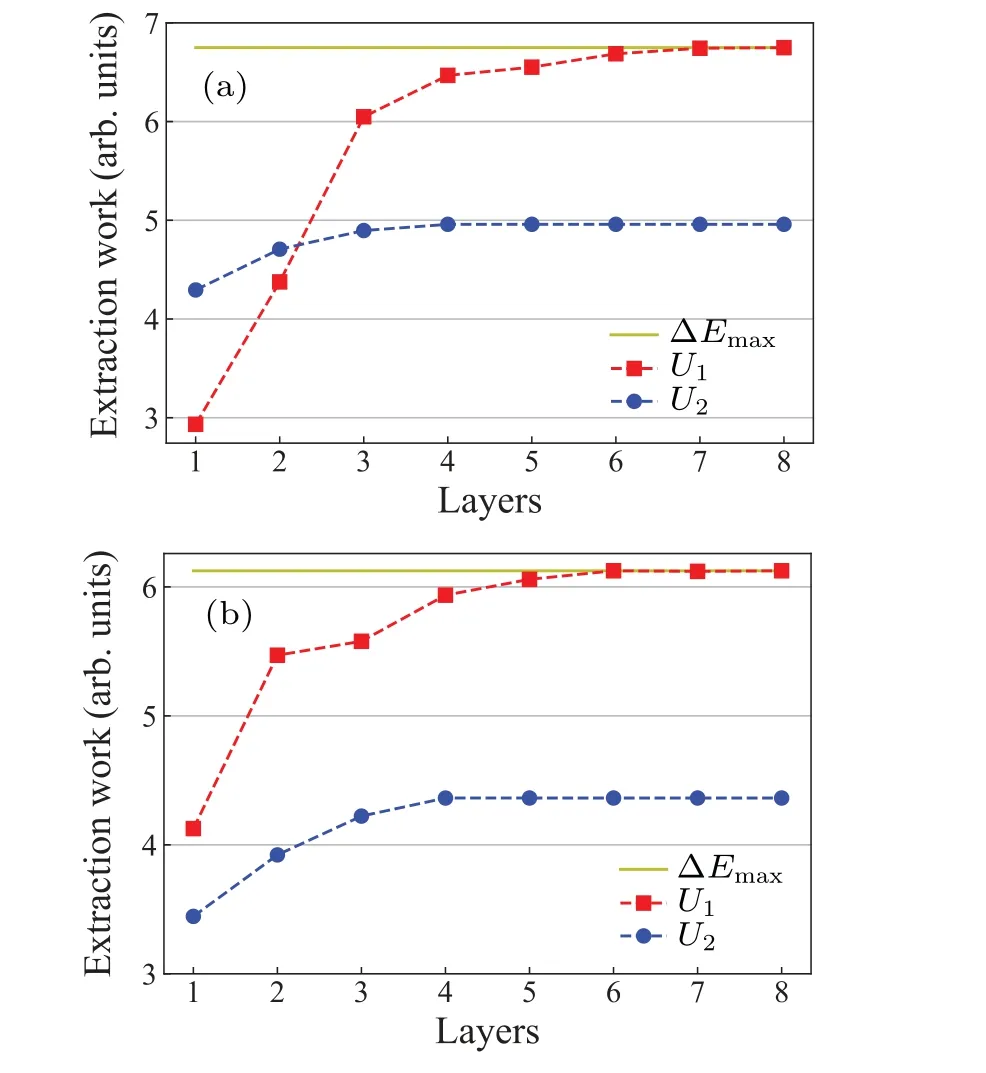
Fig.5.Capacity of work extraction for different ansatz U1 and U2 as given in Fig.4,showing that the ansatz U1 can give to the maximal extractable work ∆Emax.The initial density matrix is diagonal in panel(a)and non-diagonal in panel(b).
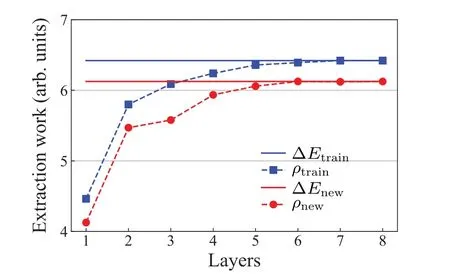
Fig.6.Generalization ability of variational quantum algorithm for work extraction.The unitary evolution trained for the initial state ρtrain with maximal work extraction ∆Etrain can give the maximal work extraction∆Enew for a new initial state ρnew, once ρnew has the same ordering of mixing as ρtrain (see Eq.(8)).
4.2.Energy extraction with work storage
The work storage is represented by a continuous variable and is initialed in the state of zero Fock number|0〉.
For the case of strict energy conservation, we consider two strategies for optimal work extraction.Firstly, we insert the optimal unitary operatorU1(θ*)obtained without the work storage directly intoCUas shown in Fig.6 for evaluations of the transferred work.Secondly, we directly optimizeθinC(θ)by maximizing the transferred work, and the optimalθis denoted as ˜θ*.For the case of average energy conservation,the obtained optimal unitary operatorU1(θ*)without the work storage is used for constructing the optimalAUfor maximal work extraction.
It is clear from Fig.7 that all three are capable of transferring work.The transferred work ofAUis always equal to the extracted work from the system byU1(θ*)in it,and when the depth of the circuit is sufficient,AUsucceeds in transferring all the extracted work to the work storage without any loss of work.In contrast, while inserting the optimalU1(θ*) directly into theCUalso succeeds in transferring work, it only transfers a small fraction of the ergotropy.This limitation is inherent to this approach.As the method of optimizingθdirectly inCU(θ) by maximizing the transferred work requires far more computation than the previous two methods,we limit the quantum circuit depth to less than 6.It can be seen that when the number of layers is less than or equal to 6,the method can achieve a much better result than plugging the optimumU1(θ*)directly intoCU.However,it is still not possible to extract and transfer the maximum extractable work,as expected.
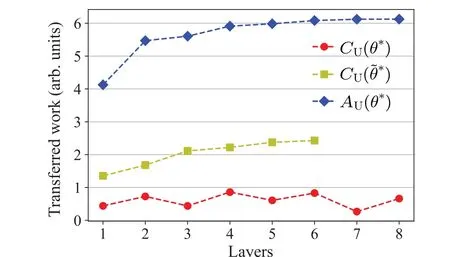
Fig.7.Comparison of optimal work extractions for three different cases.For strict energy conservation, the CU(θ*) inserts the U(θ*)obtained for maximal work extraction without the work storage, while the CU(˜θ*)is obtained by maximizing the work transfer from the system to the work storage.The A(θ*)corresponds to the case of energy conservation on average.
We also investigated the distribution of the probability density of the position of work storage before and after transferring the work,and we selected the results of the distribution of the position of each of the three cases when the respective transferring work reaches the maximum value,and the results are shown in Fig.8.

Fig.8.Comparison of the displacements of the working storage after the three different unitaries (CU(θ*), CU(˜θ*), and A(θ*)) performing on the initial state of zero Fock number|0〉.
The green line shows the initial probability density distribution, with the particles concentrated at position 0.The red curve is the result of the youngestCU(θ*), which has a more uniform distribution of positions, with the overall average position shifted slightly to the right from the initial position.The yellow curve is the result of the youngestCU(˜θ*),whose overall distribution shape is similar to that ofCU(θ*),but the overall shift to the right is larger.The blue line is the result of the calculation of the youngestAU(θ*), and the image result shows two obvious peaks,which correspond to the probability density distribution of the initial state,and their coordinates correspond to the transfer work from thstate to thestate.
5.Conclusions
In summary, we have proposed a variational quantum simulation of optimal work extraction for quantum systems with work storage described by a continuous variable.We have considered energy conservation in the unitary transformation for work transfer both in a strict way and on average.In both scenarios,we have proposed their implementation with quantum circuits and the optimal work extractions using variational quantum algorithms.We have shown that the maximally extractable work can only be realized for energy conservation on average,which has been verified by numeral simulation with a fully connected quantum Ising model.While our work focuses on the digital quantum simulation of work extraction, the variational quantum algorithm developed here may be useful for exploiting work extraction by optimizing the cyclic varying control fields in more realistic setups.
Acknowledgements
Project supported by the Guangdong Basic and Applied Basic Research Fund (Grant No.2023A1515011460) and the National Natural Science Foundation of China (Grant No.12375013).
- Chinese Physics B的其它文章
- Unconventional photon blockade in the two-photon Jaynes–Cummings model with two-frequency cavity drivings and atom driving
- Effective dynamics for a spin-1/2 particle constrained to a curved layer with inhomogeneous thickness
- Genuine entanglement under squeezed generalized amplitude damping channels with memory
- Quantum algorithm for minimum dominating set problem with circuit design
- Protected simultaneous quantum remote state preparation scheme by weak and reversal measurements in noisy environments
- Gray code based gradient-free optimization algorithm for parameterized quantum circuit

