Behaviors of cavitation bubbles driven by high-intensity ultrasound

Chen-Yang Huang(黄晨阳), Fan Li(李凡), Shi-Yi Feng(冯释毅), Cheng-Hui Wang(王成会),Shi Chen(陈时), Jing Hu(胡静), Xin-Rui He(何芯蕊), and Jia-Kai Song(宋家凯)

Shaanxi Key Laboratory of Ultrasonics,Shaanxi Normal University,Xi’an 710119,China

Keywords: ultrasonic cavitation,multi-bubble system,translational motion of bubbles

1.Introduction

Due to the secondary acoustic radiation generated by cavitation bubbles in ultrasound fields, bubble–bubble interactions should be considered to explain cavitation effects,such as the promotion or suppression of bubble oscillations,[1]which also depend on the splitting, polymerization, and nonspherical deformation of bubbles.[3–6]When multiple bubbles coexist in cavitation field,the coupling effect of bubbles cannot be ignored.Haghiet al.[7]studied the collective nonlinear behaviors of bubbles in polydisperse bubble clusters, and found that the large microbubbles in clusters can force the small microbubbles to generate periodic frequency doubling and subharmonic oscillation.Gohet al.[8]observed the interaction between a spark-induced oscillating bubble and another bubble attached to a plate.It is found that when bubbles are close to the plate,they will produce jets towards or away from the plate,and the jet direction is closely related to the oscillation time of the bubble, which provides experimental support for reducing cavitation damage.Due to bubble–bubble interactions,bubbles may attract or repel each other,which results in instability,coalescence,and fragmentation of bubbles.Considering the influence of the acoustic wake effect,the oscillation of cavitation bubbles can be enhanced because bubbles obtain more sufficient expansion through the delayed propagation of ultrasounds.Therefore, the bubbles located in the center of clusters might have the longest life and larger oscillation amplitude.Outer bubbles collapse towards central bubbles, which leads to the formation of jets.[9,10]Therefore, the typical behaviors of bubbles should be affected by the boundary closely related to the distribution of the pressure field in liquid.

Cavitation behaviors are very complicated due to the multiple interactions in the multi-bubble cavitation field.Secondary Bjerknes forces between bubbles are considered to account for the bubble–bubble interactions.Lanoyet al.[11]explored the potential influence of secondary Bjerknes forces on bubbles in microfluidic devices, as noncontact manipulation carriers to attract or repel bubble.Therefore, the secondary Bjerknes forces play a key role in the aggregation of bubbles, which are closely related to translational motions of bubbles.Doinikov[12,13]introduced a general model to explore the translational motions of bubbles in water driven by strong acoustic waves.It is predicted that the forces can make bubbles aggregate together.Zilonovaet al.[14]developed a model to study the dynamics of bubble–bubble interactions by considering the viscoelastic drag effect of viscoelastic medium.They found that due to the influence of elastic resistance on bubble motions, dynamical steady states can be obtained.Wanget al.[15]studied the effect of burst ultrasound on the translation and pulsation of double bubbles,and found that shortening the time interval of a burst and increasing the acoustic amplitude can enhance the translation of bubbles.Thus, bubble motion can be controlled by adjusting the distribution of the acoustic field and environmental parameters.

However, the complexity of bubble behaviors leads to more uncertainty, especially in chaotic acoustic field.Selforganization of bubbles occurs in high-intensity acoustic filed,and bubble streams with high bubble concentrations can be observed.High-intensity ultrasonic wave radiated from the ultrasonic horn induces bubbles to accumulate below the horn tip,and strong cavitation can be generated.[16]Yasuiet al.[17]developed a model to explain strong interactions among bubbles by introducing the coupling effect of bubbles,which conduces to predicting their translational movements by using the interacting forces on bubbles in the near filed of ultrasonic horns.Different bubble cluster structures can be observed near the tips of ultrasonic horns,[18–20]such as “mushroom”, triangular/conical, and filamentary patterns.It is also demonstrated that within a certain range,liquid properties and structure geometries have little effect on attached cavitation.However,the radiation intensity and emitting surface size of sonotrodes may significantly result in different cavitation effects.[18]Cavitation with high bubble concentration is very complex.The negative pulse radiation was observed experimentally and predicted theoretically,[21,22]which is related to the strong interaction among the bubbles with different sizes.Coalescence and fragmentation of bubbles occur all the time.Bubble fragmentation may generate acoustic emission, which might be the source of low-frequency cavitation noise.[22]To the best of our knowledge, the detailed behaviors of cavitation bubbles just below an ultrasonic horn have little been explored due to the fast translational movement of bubbles and high bubble concentration, which hinder directing observations of local bubbles.Although the suppression or promotion mechanism of coupled oscillations in multi-bubble systems has been verified experimentally and theoretically, there are still many unknowns for these aspects.The coalescence and fragmentation might be enhanced by translational motions of bubbles,which may affect the utility of cavitation energy.

In this paper, in order to obtain an insight into bubble–bubble interaction in a strong acoustic field,translational motions of bubbles with a radius less than 10 µm near an ultrasonic horn are traced by videos captured by a high-speed camera.We focus on the bubble behaviors with a radius of less than 10µm,which are difficult to study by conventional observation.It is found that translational motions of bubbles are always accompanied by coalescence and fragmentation of bubbles.Cavitation noise indicates strong negative pressure radiation,possibly originating from the violent collapse of cavitation bubbles.However, it is observed that tiny translating microbubbles in this chaotic field do not oscillate with a large radial amplitude, which might be related to the translational motion,mass transfer,coalescence,and fragmentation of bubbles.In order to include this multiple interaction,we propose a nonlinear model of triple-bubble system to describe the motions of these microbubbles.

2.Experimental observations

An ultrasonic horn driven by an ultrasonic generator(Qingda Sonic, China) was immersed in water 25 mm under the water surface and a large number of cavitation bubbles were generated.The electric power of the ultrasonic generator was about 400 W.The diameter of the horn tip was 20 mm.The operating frequency of the horn was 20 kHz.A highspeed camera (Phantom T3610, Vision Research, Inc., USA)was connected to a computer.The motions of cavitation bubbles generated within 0.5 s of the start of the transducer operation was observed and recorded by using different frame rates with a light source placed behind the transparent tank(20 cm×10 cm× 15 cm).The height of water in the transparent tank was about 100 mm.At the same time,the acoustic pressure was measured by a hydrophone (Miniature Hydrophone Type 8103, Bruel & Kjar, Denmark) connected to the oscilloscope (4 Series Mixed Signal Oscilloscope, Tektronix Inc., USA).The observation area was marked by a dashed box as shown in Fig.1.

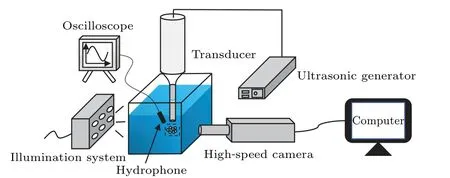
Fig.1.Schematic diagram of experimental setup.

The target bubbles were observed by macro lens (Milvus 2/100M ZF.2, Carl Zeiss AG, Germany) at a frame rate of 5×104fps as shown in Fig.2.The black part at the upper part in each image was 2 cm in diameter transducer tip.Bubbles were found to be generated on the vibrating horn surface,and moved outward away from the surface at a certain speed.There were many dispersed tiny microbubbles and clusters subjected to strong interactions.In order to observe the behaviors of these dispersed tiny microbubbles in the region circled by the red dots, a long focal length microlens(Navitar Zoom 6000, AMETEK, Inc., USA) was mounted on the camera.It is worth noting that the observed region was very close to the central axis of the horn tip, with a vertical distance of about 5 mm away from the tip.Therefore, microbubbles were amplified,but the scope was very limited.

Fig.2.Generation of microbubbles below tip of the transducer, with observed area of long focal length microlens marked by red dots,and its scope varying with shooting frame rate.

2.1.Coalescence and fragmentation

Driven by high-intensity ultrasound, bubbles oscillate,accompanied by coalescence and fragmentation.The nonspherical oscillations affect bubble stability, and eventually leading the bubble to collapse.[23–26]Therefore, bubble behaviors might be disturbed by neighboring bubbles.Figure 3 shows bubble behaviors observed by the long focal length microlens with a recording rate of 4.5×105fps at a resolution of 256×128 pixels(each pixel of the images is about 1µm),and the observation region was about 256 µm×128 µm.In Fig.3(a), a bubble with a radius of about 12 µm was splitting into two and more daughter bubbles, which aggregated into one bubble again after about 4 cycles.Initially, the bubble was almost spherical.However, non-spherical shapes appeared during translation,e.g.,an“arrow”shape at 56µs,followed by a“layered pie”at 62µs,and then the fission evolution continued until 178µs,finally coalesced into a spherical bubble at 267µs.In Fig.3(b),there are two 5-µm bubbles with a distance of about 78µm in between.It is found that bubble fission occurred at about 13µs,followed by asynchronous coalescence at 22µs.The fission state of the upper bubble lasted about 25 µs, while the lower lasted about 9 µs, and the time intervals are both less than one cycle.Figure 3(c) shows the interaction between two bubbles of unequal size.It is observed that bubble fission(89µs–220µs)was followed by an engulfment process(0µs–73µs).From the comparison among the above 3 cases,it is found that for unstable microbubbles,their evolution processes are similar, all of them fissure, and then coalesce.It is worth noting that the observation zone was close to,but not just below,the radiation surface of the horn,where highly concentrated and strongly oscillating bubbles were presented.Moreover, due to shielding effects, the microbubbles did not always oscillate violently.In these photos,there were dots in the background that could be background noise or bubbles that are not in the focal plane.

Fig.3.Microbubbles below ultrasonic horn.(a)Strong interactions among daughter bubbles,(b)twin bubbles,(c)strong interactions between coupled bubbles.See supplementary videos 1–3.

We adjusted the frame rate to 3×105fps at a resolution of 640×192 pixels,and each pixel was about 1µm as shown in Fig.4.Firstly,the translating microbubble oscillated almost spherically during 0 µs–50 µs.After a sudden non-spherical deformation,a first fragmentation occurred,with two daughter bubbles appearing at∼57µs and then coalescing into an ellipsoidal bubble at∼67µs.The unstable oscillation of the ellipsoidal bubble lasted about 27µs before splitting into twin bubbles again(seen in the image at 97µs).Twin bubbles bounced off at an initial velocity of about 3.5 m/s, and the maximum spacing distance was about 24 µm at∼107 µs, and then the twin bubbles underwent radial oscillation with a small amplitude for∼15µs.With the oscillating amplitude of twins increasing, their interactions were strengthened, which brought them together again to form a bubble at∼163µs.Therefore,oscillation behaviors of bubbles were sensitive to liquid environments and acoustic fields.Daughter bubbles could bounce away from each other and recoalesced.It is reasonable to predict that bubble fission may occur during collapse and rebound stages of nonlinear pulsating bubbles.

Fig.4.Entangling of twin bubbles.See supplementary video 4.

2.2.Translational motions of bubbles

Because of the effects of bubble stream below the horn tip, all the bubbles were translated in the liquid, which might increase the possibility of bubble coalescence.Three groups of translating bubbles were traced as shown in Fig.5,which were captured under the same conditions as those in Fig.3.Bubble sizes were similar and range from 2 µm to 7 µm.From the trajectories presented in this image at 467 µs in Fig.5(a), it can be seen that bubbles 1 and 2 kept slowly approaching to each other without collision within about 10 cycles.By contrast, bubble 3 obtained the smallest horizontal displacement.Therefore, we predicted that the three bubbles attracted each other.For the case in Fig.5(b),it is found that the trajectory of bubble 3 is almost vertical,which means that its translational motion is less affected by bubbles 1 and 2.Within about 5 cycles, bubbles 1 and 2 attracted each other and then coalesced into a new bubble, which is named bubble 4, in a very short time(about 4µs).Unlike the case in Fig.5(a), the attraction between bubbles 1 and 2 was dominant.Moreover, bubble 4 maintained the translational direction of bubble 1 or bubble 2.For the case in Fig.5(c), the morphologic transformation of bubbles is complicated.In the beginning,bubbles 1 and 2 attracted each other,and could be observed that a jet was emitted from bubble 1 towards bubble 2 at∼4 µs; and then the two growing bubbles coalesced into an ellipsoidal bubble at 9µs,followed by an arrow-like shape and the second fragmentation in a non-spherical pattern.The trajectories are marked in the image at 133 µs, and it is found that trajectories of bubbles 1 and 2 showed distinct peak bending parts during the strong interacting period(around 10µs–20µs),which means that the strong interaction between two bubbles has a significant effect on translational behaviors.It is also reasonable to conclude that the coupling effect of bubbles plays a dominant role only at a limited distance.From the observations it is found that moving bubbles transfer their mass at gas–liquid interfaces,which might lead to a channel formed between two approaching bubbles, thus they coalesced.The fragmentation and coalescence of bubbles usually occurred at a very short interval,accompanied by violent non-spherical deformation.

Fig.5.Translational motions of a multi-bubble system.(a)Case 1:trajectories of three coupled bubbles,(b)case 2:coalescence of translational bubbles,(c)case 3: translational motions of two strong interacting bubbles.See supplementary videos 5–7.

The oscillation and spacing of bubbles were traced too as shown in Fig.6.Here some points ofR–tcurves of bubbles might be lost when bubbles were too small to be identified.Figures 6(a)–6(c) show the radial pulsations of bubble 1, bubble 2, and bubble 3 (in Fig.5(a)), respectively.Initial radius of bubbles 1 and 2 were∼2.5 µm, and that of bubble 3 was∼3.5 µm.As can be seen from the figure, the radial pulsations of three bubbles were almost in phase.In the fifth acoustic cycle,pulsations were enhanced,and then equilibrium radii of the first two bubbles expanded, which might be due to the mass transfer through bubble surfaces.[27,28]Several violent collapsing spikes were observed (marked by empty circles),which might be related to abrupt perturbations of the surrounding acoustic pressure and strong interactions among bubbles.According to the radial oscillations, we predicted the secondary radiation pressures of bubbles as shown in Figs.6(d)–6(f).It can be clearly seen that some negative spikes on these curves, first discovered by Versluis,[21]might lead to asynchronous collapses of bubbles.[22]Although the secondary radiation was very weak,the accumulation of bubbles could generate a strong effect on surrounding medium.

In Fig.6(g), relative displacements of bubbles (in bubbles Fig.5(a)) are shown.It was found that bubbles 1 and 3 approached to bubble 2 at similar relative speeds and translational motion of bubble 1 should be suppressed to some extent.Figure 6(h) shows that the coalescence of bubbles 1 and 2 occurred within two acoustic cycles, and the new bubble 4 moved faster than bubble 1.Comparing Fig.6(h) with Fig.6(i), it is found that if the distance between two bubbles in a multi-bubble system is less than 30µm,besides the possibility of merging into bubbles, the translational motion will be strongly disturbed in the first acoustic cycle.Accordingly,for tiny micro-sized bubbles, it was predicted that bubble interaction would be weak when their spacing was greater than a critical distance of 30µm.There were many bubbles undergoing complex motions in the liquid near the ultrasonic horn tip,and more examples can be found in Fig.7.It verified that if the spacing distance between bubbles is smaller than 30µm,the possibility of coalescence increases.Because of the high concentration of bubbles, the strong interactions among bubbles play a critical role in determining the features of their behaviors,especially shape oscillations,however,these influences should be limited for tiny microbubble due to shielding effects.[29]

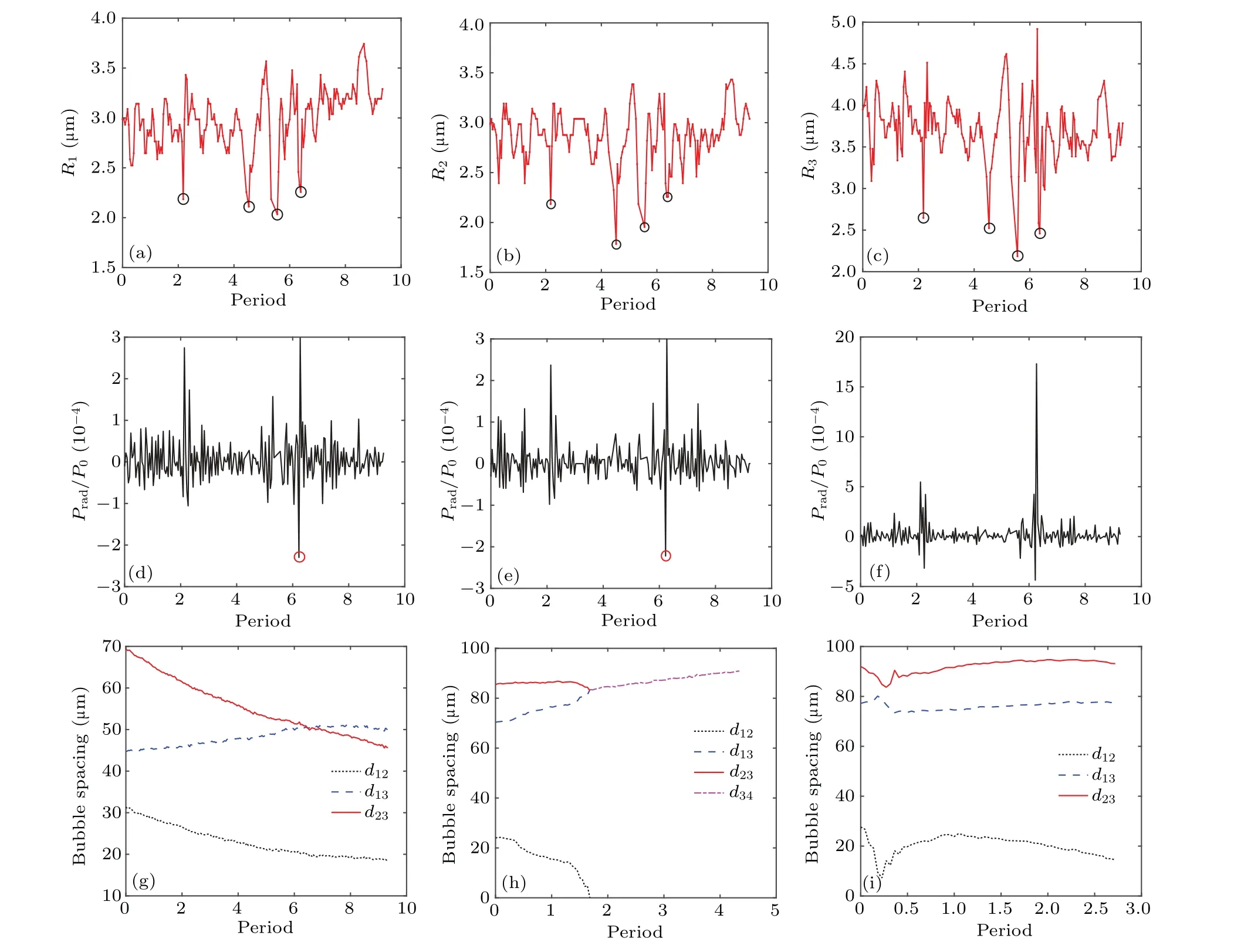
Fig.6.Tracking movements of bubbles in Fig.4.Radial pulsations of(a)bubble 1, (b)bubble 2, (c)bubble 3; and radiation pressure normalized by static pressure P0 of(d)bubble 1,(e)bubble 2,and(f)bubble 3 in Fig.4(a);spacing between bubbles for(g)case 1,(h)case 2,(i)case 3.

2.3.Cavitation signals

The shock wave generated by the bubble rupture can be obtained by the signals collected by the hydrophone, so we can obtain a lot of information about the bubbles from the cavitation signals.[30]The signals measured by hydrophone in the cavitation liquid are shown in Fig.8(a).Bubbles are in a strong negative pressure environment,which might be caused by strong interactions of bubbles with different equilibrium radii.[22]The power spectrum indicates that the fundamental component was dominant in this cavitation field (Fig.8(b)).Due to nonlinear effects,there were harmonics,subharmonics,and broadband noise.The higher the harmonic order,the lower the intensity of harmonics is.Subharmonics may be obtained from prolonged expansion phases and delayed collapse phases of cavitation bubbles,[31]which can be observed on curves marked by circles in Figs.6(a)–6(c).In addition, figure 8(b)shows that broadband noise is suppressed near the fundamental and harmonic frequencies.The broadband noise and abundant harmonics were co-existent, which is attributed to the coexistence of inertial cavitation and stable cavitation.[32,33]Figure 8(c) presents a spectrogram of signals by short-time Fourier transform.It can be seen that the broadband noise was random to some extent and its low frequency components were always present.The low-frequency noise might be caused by the coalescence and fragmentation of bubbles.

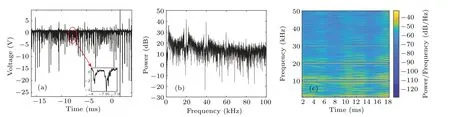
Fig.8.Analyses of(a)representative time-domain signal,(b)power spectrum of the signal,and(c)spectrogram of signal.

3.Mathematical model

Many investigations have been done on bubble dynamics by considering bubble–bubble interactions in multi-bubble systems,[7,12,15]where a bubble pair is the simplest model.According to our observations, it is found that translational motions of cavitation bubbles are usually accompanied by coalescence and fragmentation of bubbles, and strong interactions of bubbles might result in acoustic emissions of negative pressure.To explain the evolution of bubbles in these complex cases,we constructed a three-bubble system,as shown in Fig.9.To simplify,it was assumed that bubble 3 was fixed on theyaxis with coordinate (h, 0), and bubbles 1 and 2 moved along thexaxis, maintaining spherical oscillations.x1andx2were position coordinates of bubble 1 and bubble 2.Distances between bubbles were denoted byd12,d13,andd23,and subscripts represent different bubbles.Instantaneous radii of bubbles wereR1(t),R2(t), andR3(t), respectively.Due to the influence of the secondary radiation of oscillating bubbles,averaged secondary Bjerknes force between bubble 1 and bubble 2 can be given as[34,35]

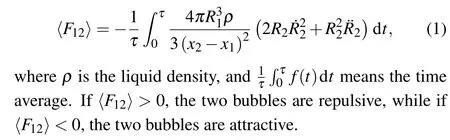
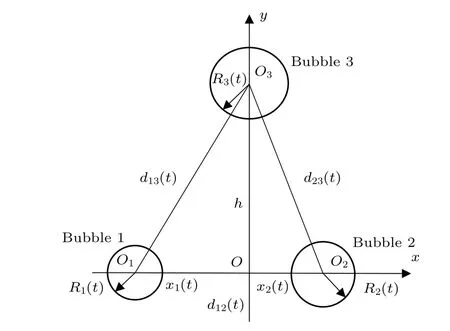
Fig.9.Three-bubble system.

In unbounded liquids,for the radial oscillation and translational movements of bubbles, coupled equations can be given as follows:[12,15]

wherecis the sound speed in the liquid,Pis the ambient pressure,σandµare the liquid surface tension and viscosity coefficient.Equations(2)and(3)represent pulsations and translations of bubble 1 and bubble 2, respectively.Equation(4)represents the radial oscillation of bubble 3.The driving acoustic pressurePd(t)=-Pasin(2π ft),withPaandfbeing the amplitude and frequency.The pressurePsk(k=1, 2,and 3)at bubble walls can be expressed as

Based on the above dynamic equations, the translational motion of bubbles will be simulated and compared with the experimental results in the following.

4.Numerical simulations

4.1.Verification of model

Based on the experimental observations, bubble movements show three translational patterns: triangular layout(Fig.5(a)), accompanied by coalescence (Fig.5(b)), and strong tangling of bubbles (Fig.5(c)).To verify the model introduced in Eqs.(2)–(4),we set the values of the parameters according to cases 1 and 2 in Fig.5, which are presented in Table 1.

Table 1.Parameters used in numerical calculation.

In the table,R10,R20, andR30represent the initial radii of bubbles 1, 2, and 3, respectively.The numerical results are shown in Fig.10, and it is found that if the bubbles are smaller than 3 µm, the oscillation amplitude are relatively weak.The comparisons among the radial motion of bubbles with the curves in Figs.6(a)–6(d)show that they are obviously different,which might be caused by neglecting the multiple interactions.In Figs.10(c)and 10(d),the translational displacements are represented by solid line for theoretical results and the dashed lines for traced lines in experiments.Similar trend can be found for the two results.

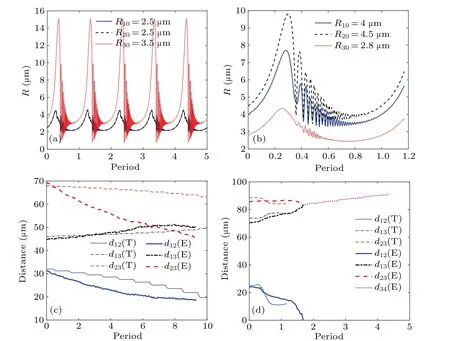
Fig.10.Diagram of theoretical simulation and experimental data of [(a), (b)] bubble radius and [(c), (d)] distance between bubbles over time.The values of these simulations are chosen from [(a), (c)] case 1, [(b), (d)] case 2 in Fig.4, with (T) and (E) denoting theoretical and experimental data respectively.

Theoretical simulations overestimated the expansion radii of bubbles in Figs.6(a)–6(c), which might be caused by following possible factors.First, the radiation of the transducer was modulated by periodic currents, and we did not consider fluctuations in acoustic radiation intensities in numerical calculations.Second, bubble clusters acted as acoustic shelters,leading to anomalous absorption of acoustic energy.Third,due to the image magnification, only localized bubbles were captured,while oscillating bubbles with large amplitude were not tracked.Fourth, translational movements of bubbles in liquids with a high concentration of bubble nuclei increased the possibility of nuclei absorption,which may weaken bubble oscillations.Thus, bubble behaviors in multi-bubble systems may be influenced by many factors, and translational motion may play an important role in instantaneous cavitation field.The theoretical model can only be used to predict the trend of the bubble movements.

4.2.Translational motion of bubbles

4.2.1.Effect of bubble sizes

According to our observations,the size of cavitation bubbles was distributed in a wide range.Effects of bubble equilibrium radii were investigated in two cases,e.g., case 4:R10=6 µm, andR20=7 µm (Figs.11(a) and 11(b)); case 5:R10=3µm andR20=7µm(Figs.11(c)and 11(d)).The equilibrium radius of bubble 3 is chosen to be in a range from 3µm to 15µm withx10=-15µm,x20=25µm,h=40µm,f= 20 kHz, andPa= 116 kPa.The interaction between two bubbles might be quite different when the third bubble is present.For the bubble pair with radii of 6 µm and 7 µm,the repulsion was observed,and there existed a steep rebound of the bubble spacing.Translational modes,such as repulsion,attraction,and stabilization spacing,can be observed from numerical calculations.In the multi-bubble system, the disturbance of surrounding bubbles cannot be neglected,which may lead to an unstable response of the bubble pairs to translational motion, so coalescence and fragmentation of bubbles should always exist.[36]These predictions accord well with previous experimental observations in Section 2.Numerical calculations have also verified that the equilibrium distance of bubble pair is affected by the sizes of surrounding bubbles.[37]

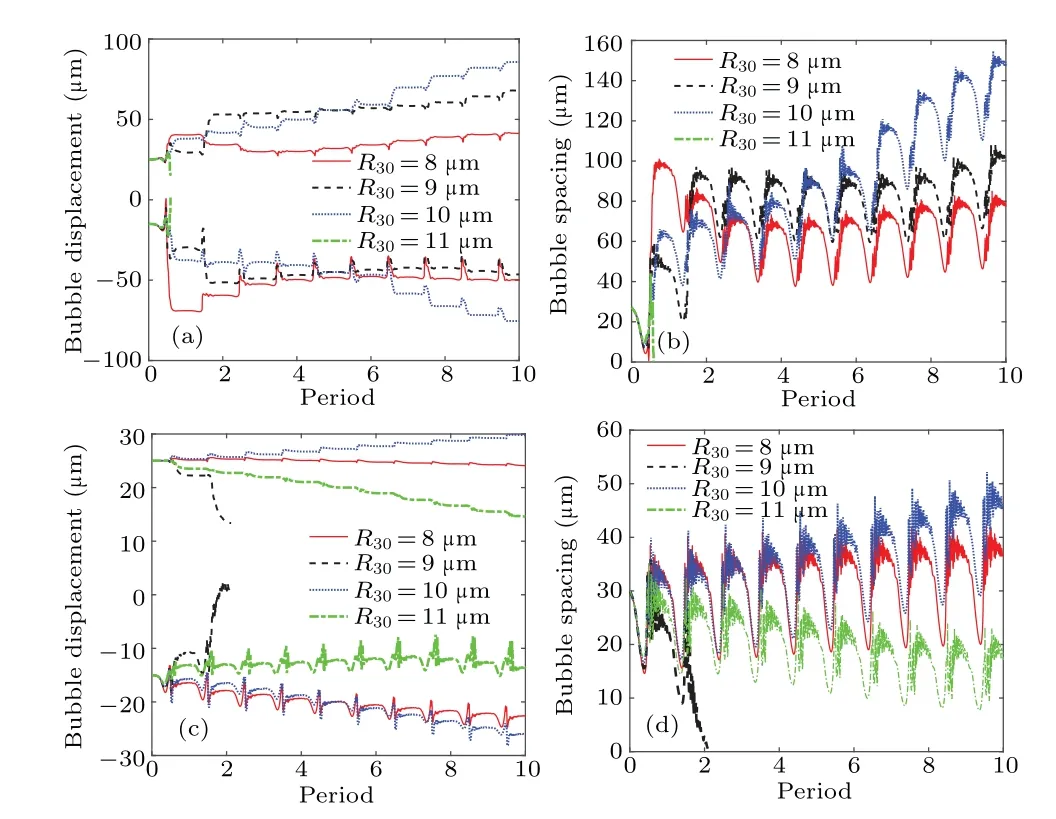
Fig.11.Bubble repulsion,displacement,and spacing of bubbles in[(a),(b)]case 4,and[(c),(d)]case 5.

4.2.2.Effect of third bubble position

The effect of the third bubble on translational movement of the bubble pair should be limited within a finite distance.We adjusted the position (h) of the third bubble on theyaxis.The displacement and spacing of bubbles are shown in Figs.12 and 13.Whenhincreases from 30µm to infinity forR30=8µm and translational motions are represented by colored curves.As can be seen from Fig.12(case 6:R10=3µm andR20=4 µm), the bubbles have attracting tendency, and the approaching time increases with the distancehdecreasing.Therefore,the coalescence of a bubble pair can be manipulated by the third bubble.In contrast,translational motions of case 4(in Fig.13)are very different under the same conditions,and there are bounce, repulsion, and attraction of the bubble pair,in which the mode conversion can be adjusted by the position of the third bubble.Therefore,the position of the third bubble has a significant influence on translational patterns of bubble pairs.

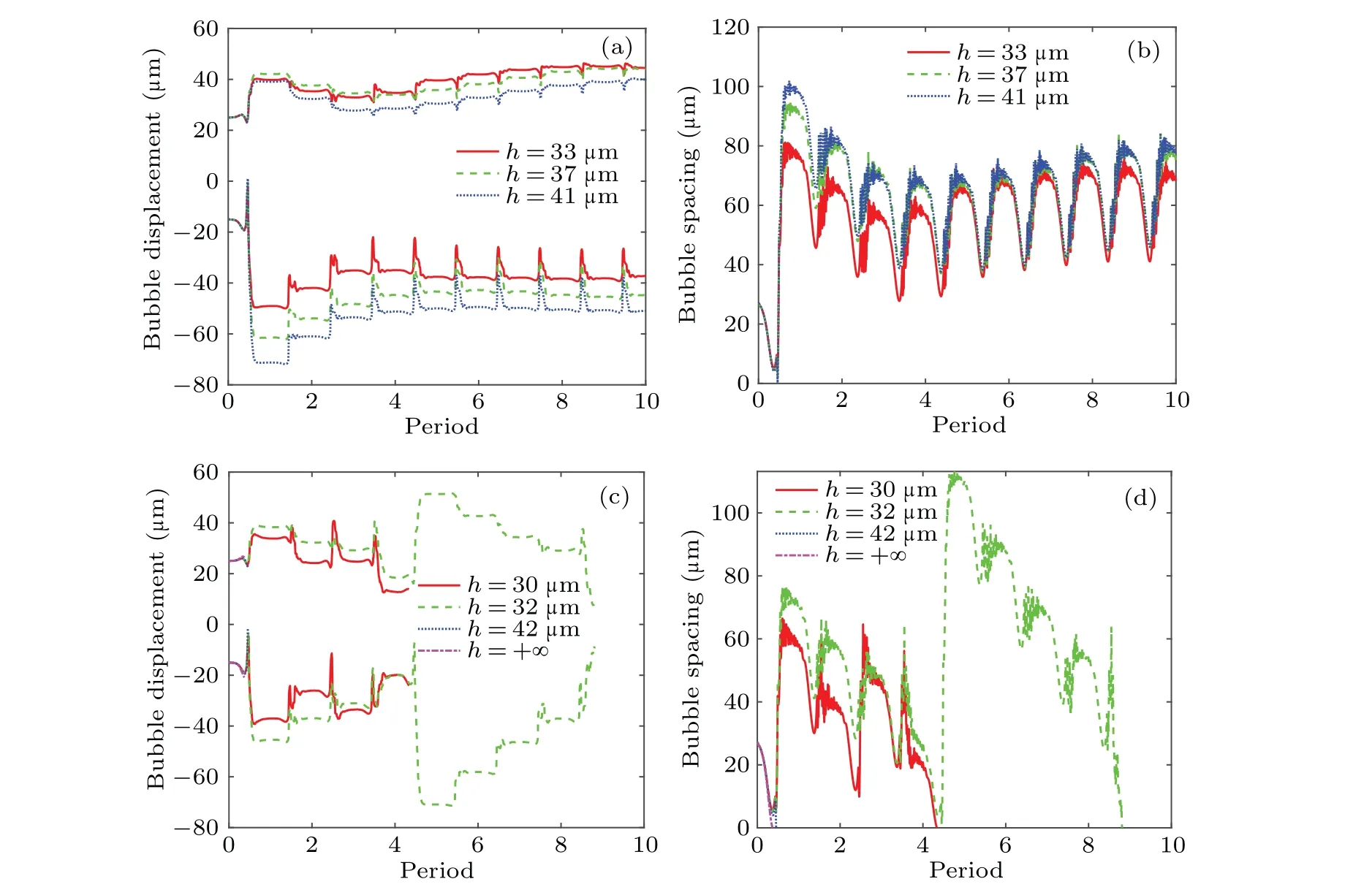
Fig.13.Bubble rebound,coalescence,or moving with a certain fluctuating distance.[(a),(c)]Displacements of bubbles 1 and 2 and[(b),(d)]bubble spacings for case 4 with R10=6µm,R20=7µm.

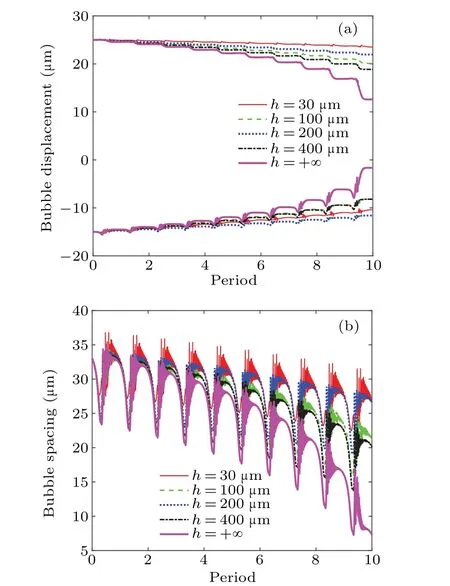
Fig.12.(a)Displacements of bubbles 1 and 2 and(b)bubble spacings for case 6 with R10=3µm,and R20=4µm.

4.3.Secondary Bjerknes forces on bubbles

According to the spectra in Fig.8, there are many frequency components in cavitation fields,and bubble behaviors might be affected by these secondary acoustic emissions.Relative translational movements should be closely related to interactions among bubbles,which could be demonstrated by the secondary Bjerknes force on bubbles.Maps of the force are presented in the acoustic pressure-frequency plane, as shown in Fig.14 with parametersx10=-160 µm,x20=140 µm,h=300µm.R30=2µm,8µm,and 14µm.For case 4(first row in Fig.14),the force is always negative in the entire range of calculation parameters.Thus, the bubble pair is attractive.For cases 5 and 6, some gray stripes and regions with positive force are found, in which the bubble pair are repulsive.The nonlinearity of this system affects acoustic responses of bubbles,and distributions of the secondary Bjerknes force between bubbles are significantly different when the size of third bubble varies.The force distribution exhibit that some regions are separated by curved contour lines in the low frequency range and low pressure range, while narrowband distribution with alternating color contours appears in the high-pressure range.Moreover,bubble repulsion also occurs in this region.

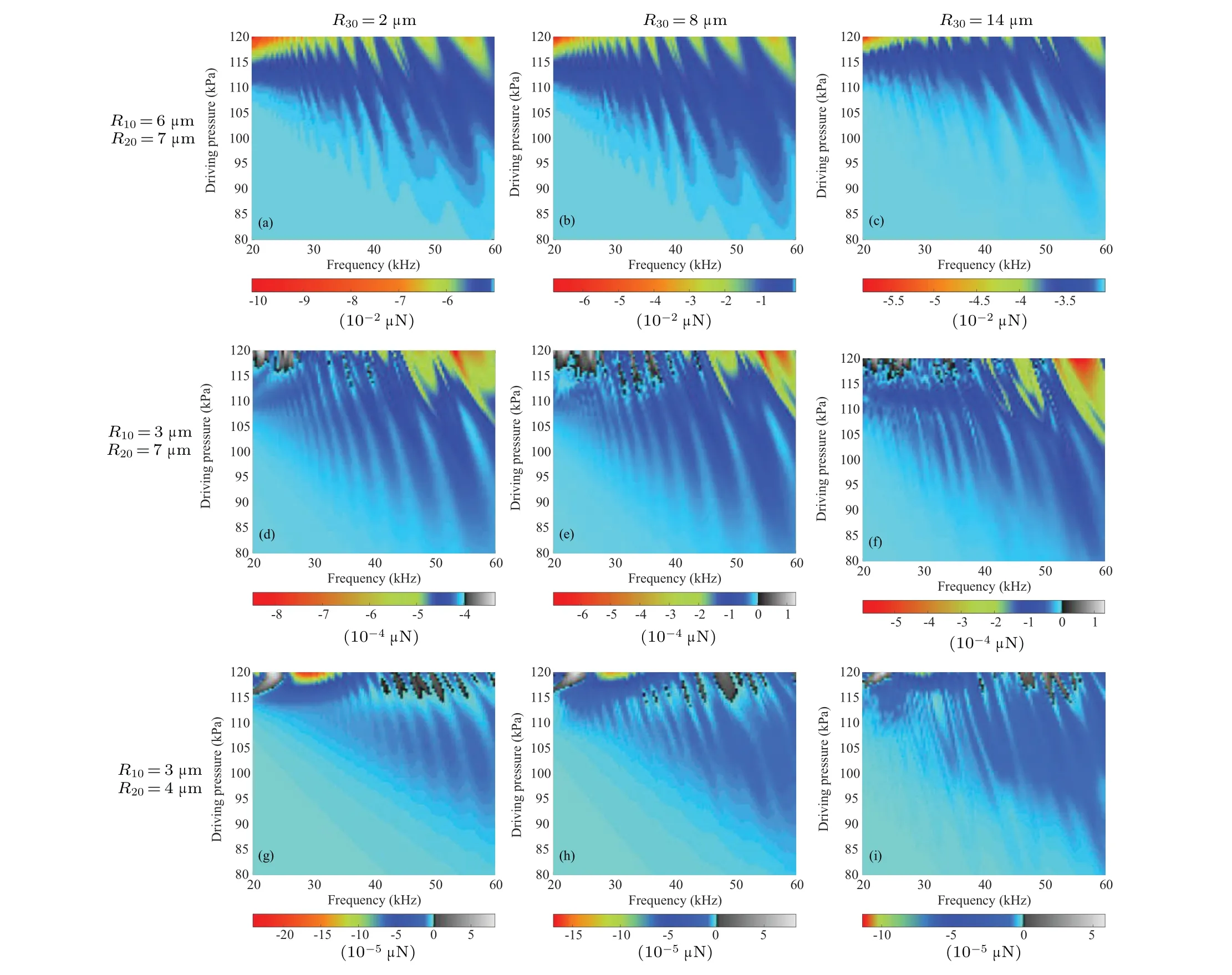
Fig.14.Maps of the secondary Bjerknes force between bubbles 1 and 2 in the acoustic pressure-frequency plane.The first row: case 4; the second row: case 5;the third row: case 6.

Based on numerical calculations, it can be concluded that there is randomness in bubble–bubble interactions because acoustic fields could be affected by acoustic emissions of strongly coupled bubbles in bubbly liquids.The coalescence of bubbles plays a crucial role in cavitation effects,and the coalescence and fragmentation of bubbles have influence on the bubble density in cavitation liquids.

5.Conclusions

The behaviors of bubbles each with an equilibrium radius less than 10 µm are experimentally observed in cavitation liquids under strong ultrasound fields generated by ultrasound horn.The coalescence and fragmentation of bubbles are recorded by videos, and the acoustic signal is measured by a hydrophone.During evolutions of bubbles, bubbles undergo engulfment and fragmentation, accompanied by emergences of different shape patterns, such as arrow-shaped and pancake-shaped patterns.The negative radiation phenomenon in signals is caused by strong interactions among bubbles of different sizes.By tracking the trajectories of three coupled translational bubbles, it is found that bubble–bubble interactions for translational bubbles can be roughly classified into three categories: (i)without coalescence or fragmentation,(ii)accompanied by bubble coalescences,and(iii)with strong entanglements between bubbles.They are closely related to patterns of translational motions, such as repulsion, attraction,and stable spacing of bubbles.In addition, for microbubble smaller than 10 µm, when the distance between two bubbles is less than 30µm,the likelihood of the coalescence increases.These phenomena have also been verified by numerical simulations with a simplified triple-bubble dynamical model proposed in this work.Besides,translational movements of bubbles are also significantly modulated by surrounding bubbles.Acoustic emissions of bubbles affect ambient acoustic fields,accompanied by coalescence and fragmentation,leading to alternating changes in bubble concentration.Therefore,bubble–bubble interactions exhibit randomness.Interacting secondary Bjerknes forces is sensitive to the acoustic frequency and pressure, the size of bubbles, and surrounding bubbles.It is of great importance to investigate the effects of translational motions of bubbles on bubble–bubble interactions in multi-bubble systems, which may highlight applications of high-intensity ultrasounds.According to comparisons between theoretical and experimental results, mass exchange may also be an important factor influencing bubble behaviors, which should be investigated in the future.It should be noted that the triplebubble model can only be used to predict the bubble–bubble interactions.In the future, we will develop a more accurate model to describe the complex behaviors of bubbles in this high concentration bubble field.

Supplementary material

Supplementary videos to this article can be found online.More video materials can be obtained by contacting the authors via email.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.11974232 and 12374441)and the Fund from the Yulin Science and Technology Bureau, China(Grant No.CXY-2022-178).