夹紧变形条件下齿轮齿廓偏差和齿距偏差的评定

丁明亮，陈鸿健

（1.中国航发哈尔滨东安发动机有限公司，哈尔滨 150066；2.哈尔滨工业大学机电工程学院，哈尔滨 150001）

0 引言

齿轮的夹紧方式一般有径向夹紧和轴向夹紧两种，在夹紧齿轮后进行磨齿加工时，受到夹紧力场和磨削力场的耦合作用，导致相对于初始的安装位置会有偏心和偏摆误差，即位姿误差，而机床上的砂轮并不会随着齿轮位置的改变而进行补偿修正，从而导致齿轮的加工精度受到影响。姜忠立等[1]通过有限元法计算得到了齿轮加工中的变形量，并根据约束条件设计出合适的齿轮专用夹具。王欢[2]以薄壁齿圈为研究对象，分析了夹紧力和切削参数之间的关系，以夹紧变形最小为目标优化，得到了扇形卡盘的扇形圆心角。巩赟[3]针对齿轮的液压膨胀式精密夹具进行了有限元分析，计算得到了加压后薄壁套筒的最大变形和夹紧力。段荣鑫[4]通过有限元仿真分析了薄壁齿轮的夹紧变形规律，并用遗传算法对夹紧力进行了优化。液压膨胀芯轴是一种高精度夹具，能使加工后齿轮的径向跳动≤3 μm[5]。航空齿轮加工精度高，精度等级需达到5级以内，成形磨削作为齿轮精加工的最后一道工序，夹紧变形误差和热变形误差能占到总误差的40%～70%，因此有必要深入分析夹紧变形对齿廓偏差、齿距偏差的影响规律，以实现磨削参数的优选，这对提高齿轮成形磨削精度具有重要意义。

1 齿轮齿廓总偏差和齿距偏差的评定方法

在齿轮磨齿加工过程中，受诸多因素的影响，实际得到的齿轮齿廓总是会与理想的渐开线齿廓有一定的偏差，这些齿廓偏差的存在会导致齿轮传动过程中不能保持恒定的传动比，产生振动和噪声，因此在GB/T 10095.1—2008的标准中对齿轮精度评级采用的是齿廓总偏差。因为实际加工得到的齿轮齿廓并不完全是渐开线，在渐开线与齿根圆连接处还有一段圆弧进行过渡，所以在计算齿廓总偏差前还要对计值范围进行界定。GB/T 10095.1—2008中规定了从齿顶圆开始到齿廓上渐开线的起始点为齿廓的有效长度LAE，齿廓的计值范围Lα为有效长度LAE的92%。实际加工得到的齿轮齿廓示意图如图1所示[6]，坐标系中的第一象限内有一条实际的右齿廓，假设已得到该齿廓上一系列测量点的坐标值（xi，yi），对于上面任一测量点K作过它的一条理想渐开线（图中的细实线），设齿廓渐开线的基圆半径为rb、K点坐标值为（xk，yk），则渐开线上K点的向径rk=、压力角αk=arccos（rb/rk）、展角θk=tan αk-αk，K点向径与X轴正方向的夹角φk为

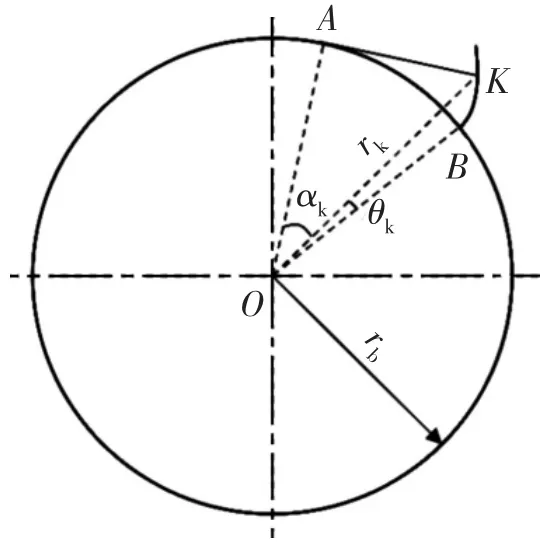
图1 实际齿廓示意图

若K点在第三或第四象限，即yk≤0时，需使φk=2πφk。得到K点的展角θk及向径与X轴的夹角φk后，则过K点的理想渐开线起始角τk=φk-θk。

首先通过计算得到各测量点上的理论渐开线起始角τi，并从一系列τi中找出τmin和τmax。根据渐开线的形成原理可知，同一基圆上两个渐开线的法向距离等于基圆上两渐开线起始点的距离，则实际齿廓的齿廓总偏差Fα[7-8]为

当实际齿廓中同时有处于第一和第四象限的测量点时，得到的τmin和τmax会相差过大，此时求得的齿廓总偏差Fα是错误的，需要对其中一些测量点的τi值进行修正。当τmax-τmin＞2π/z时，从一系列测量点中找出τi＞π的值进行修正，使τi=τi-2π，修正后再从一系列τi中找到τmin和τmax，即可得到最终的齿廓总偏差。

齿轮齿距偏差的存在会使齿轮在传动中产生振动、冲击和噪声，影响了齿轮传动的平稳性，因此在齿轮的精度等级评定时还需考虑齿距偏差的大小，GB/T 10095.1—2008中的齿距偏差有3种，分别为单个齿距偏差、齿距累积偏差和齿距累积总偏差。齿距偏差示意图如图2所示，图中实线为实际齿廓，虚线为理想齿廓，pt为单个理论齿距pt=πd/z。单个齿距偏差fpt为在齿轮的分度圆上任意两个相邻同侧齿廓的实际齿距与理论齿距之差。齿距累积偏差Fpk为任意k+1个同侧齿廓的实际齿距与理论齿距之差，理论上齿距累积偏差Fpk等于k个单个齿距偏差之和，k可从1取到齿数z。在任意齿距累积偏差中的最大齿距累积偏差为齿距累积总偏差Fp。

图2 齿距偏差示意图

当齿廓在分度圆上的点坐标值（xi，yi）已知时，利用余弦定理可以算出分度圆上相邻齿廓两点之间的向径夹角θi，则单个齿距偏差fpti可表示为[7-8]：

齿距累积偏差Fpk可表示为

通过计算得到一系列的齿距累积偏差最大值和最小值后，可求得齿距累积总偏差Fp为[7-8]

2 成形磨齿齿面参数模型的建立

齿轮夹紧变形示意图如图3所示，若在齿轮初始安装位置的中心上建立静坐标系O0-x0y0z0，在齿轮夹紧变形后的位置中心上建立工件坐标系Oi-xiyizi，则可用齐次坐标变换矩阵表示齿轮位姿。

图3 齿轮夹紧变形示意图

当工件坐标系Oi-xiyizi变换到静坐标系O0-x0y0z0时，需要绕xi轴转动Δα，绕yi轴转动Δβ，再绕zi轴转动Δθ，最后再分别沿xi、yi、zi轴平移Δx、Δy、Δz，由于转动角Δα、Δβ、Δθ都为极小的值，旋转矩阵的次序没有影响，设c代表cos、s代表sin，则齐次位姿变换矩阵为[9]

因为转动角Δα、Δβ、Δθ都为极小值，所以各转动角的cos（）值为1，各转动角的sin（）值为其转动角的弧度值，忽略变换矩阵中各项的高阶无穷小，则矩阵可简化为[9]

忽略夹紧变形时，砂轮磨齿加工得到的齿廓在静坐标系和工件坐标系下的参数方程均为标准渐开线参数方程，砂轮加工在静坐标系的位置并不会改变。但是齿轮夹紧变形以后，砂轮在工件坐标系中的位置就会发生改变，利用静坐标系与工件坐标系之间的齐次变换矩阵，可得到在夹紧变形条件下齿轮齿面方程为

根据前述齿廓偏差和齿距偏差的评定方法，则可计算在夹紧变形条件下的齿廓偏差、齿距偏差。

3 齿廓总偏差和齿距偏差的计算步骤

齿廓总偏差的计算步骤如下：1）根据齿轮夹紧变形后的位姿变化，得到齐次坐标变换矩阵rot（x，y，z），将其与标准渐开线齿面方程相乘得夹紧变形条件下的误差齿面参数方程；2）在第i个误差齿面中部的齿廓上等间距取测量点，分别计算出各测量点的展角θk、φk及τk；3）从各测量点的渐开线起始角τk中找出τmin和τmax，根据式（2）计算出该齿廓的齿廓总偏差，若偏差过大，进行修正后重新计算；4）对各轮齿重复2）、3）步，求出各齿的齿廓偏差，各齿中最大的即为该齿轮夹紧变形条件下的齿廓总偏差。

齿距偏差的计算步骤如下：1）根据齿轮夹紧变形后的位姿变化，得到齐次坐标变换矩阵rot（x，y，z），与标准渐开线齿面方程相乘得夹紧变形条件下的误差齿面参数方程；2）求出各个误差齿面中部齿廓与分度圆的交点（xi，yi），根据式（3）、式（4）可算得各相邻轮齿间的单个齿距偏差；3）根据式（5）、式（6）可算得齿距累积偏差和齿距累积总偏差。

4 位姿误差对齿廓偏差、齿距偏差的影响规律

在夹紧变形条件下齿轮产生的位姿误差可分为沿x/y轴的平移、绕x/y轴的转动、沿z轴的平移和绕z轴的转动4种，而沿z轴的平移误差对齿轮的精度评定基本没有影响，计算时忽略不计。以模数为4 mm、齿数为19、压力角为25°、齿宽为72 mm的渐开线直齿圆柱齿轮为例，假设沿y轴平移的误差Δy=3 μm、绕y轴的转动误差Δβ=0.02°，以及绕z轴转动的误差Δθ=0.2°，并取齿轮中部横截面的右侧齿廓进行分析，分析各种误差对齿轮齿廓偏差和齿距偏差的影响规律。

沿y轴平移3 μm误差条件下得到的各轮齿的齿廓偏差、齿距偏差计算结果如图4所示。由图4可见，沿y轴的平移误差对齿距累积偏差和齿距累积总偏差均会产生较大的影响，这两项偏差的最大值大约是平移误差的2倍（6 μm左右），而对齿廓总偏差影响稍小，产生的齿廓总偏差约为2 μm左右，对单个齿距偏差影响最小，产生的单个齿距偏差最大值约为1 μm，因此沿x/y轴的平移误差主要会影响齿轮的齿廓总偏差和齿距累积偏差。

绕y轴转动0.02°误差条件下得到的各轮齿的齿廓偏差、齿距偏差计算结果如图5所示。其中影响最大的是齿距累积偏差和齿距累积总偏差，偏差最大值分别约为22 μm和27 μm左右，其次是对齿廓总偏差的影响较大，产生的齿廓总偏差最大值约为8 μm，对单个齿距偏差的影响是最小的，产生的单个齿距偏差最大值在5 μm以下，因此沿x/y轴的转动误差主要影响齿轮的齿廓总偏差和齿距累积偏差。

图5 绕y轴转动0.02°误差下各轮齿的齿廓偏差、齿距偏差

当齿轮绕z轴转动0.2°时，由于绕z轴的转动误差对齿距偏差基本没有影响，仅考虑其对齿廓偏差的影响，经过计算发现齿轮上每个轮齿的齿廓总偏差大小基本相等，约为0.15 μm左右，这表明绕z轴的转动误差对齿廓总偏差的影响较小。

5 结论

本文综合考虑夹紧变形的影响，通过齐次坐标变换矩阵建立了齿轮成形磨削齿面参数方程，分析了齿轮在夹紧变形条件下位姿误差对齿廓偏差、齿距偏差的影响规律。结果表明：沿x/y轴的平移、绕x/y轴的转动这两类位姿误差主要影响的是齿轮的齿廓总偏差、齿距累积偏差及齿距累积总偏差，而对单个齿距偏差的影响较小。另外，绕z轴的转动误差对齿距偏差基本无影响，对齿廓总偏差影响较小。