基于3d Max 的水库库容计算

宋永嘉，姜文尚，罗 飞

（华北水利水电大学,河南 郑州 450046）

0 引言

我国大多数中小型水库于20 世纪50 年代 ～70 年代建成,存在工程标准低、老化失修严重等问题。同时,随着城乡建设发展,部分水库的用途与蓄水需求也随之改变,库容的改变伴随着特征水位的改变,需重新进行库容计算。在工程项目中,库容计算结果的精确度、可靠度的提高是水利工程事业发展的重要指导,更是对水利工程、水库运行管理决策与整合的技术指导。计算库容的方法有很多,传统方法是采用断面法进行水库的库容计算,为减小公式估算带来的误差,学者们在其基础上进行了改进创新,刘炜[1]对断面法水库的库容计算模型进行了几何分析,为水库库容分层计算与整体计算间的自洽性问题提供了参考。胡跃斌[2]提出库容等效断面间距的概念和计算公式,大大提高了库容计算结果的精度。以上研究均在传统公式的基础上大大提高了计算精度,但始终是基于数字与数字间的计算求解,不能直观地对库区库容进行分析。为改变传统计算方式,同时又避免传统库容计算过程中的精度损失,市面上出现了许多相应的地理信息处理软件。其中较为常见的有ArcGIS 与Global Mapper,与传统断面法相比,使用ArcGIS 与Global Mapper 进行地形分析具有效率高和精度高等优点[3-6]。这两种方法在计算能力上相比传统算法具有很大优势,但在模型展示上有所欠缺,故本文引入3d Max 软件,旨在高效计算库容的同时,为相关施工建设提供模型参考。

1 数据与方法

1.1 数据

本文以两个有改建需求的小水库为例进行计算说明,水库位于我国中部某县境内,库区狭长,库区边坡不平整,以防洪、灌溉为主,为结合水产养殖等综合利用的小（2）型水库。库区高程数据于2019 年实测得出,取水库A 高程196 m～207 m,水库B 高程191 m～199 m 进行计算,其中水库A 196 m 高程处库容为0,水库B 191 m 高程处库容为0。现场实测数据见表1。

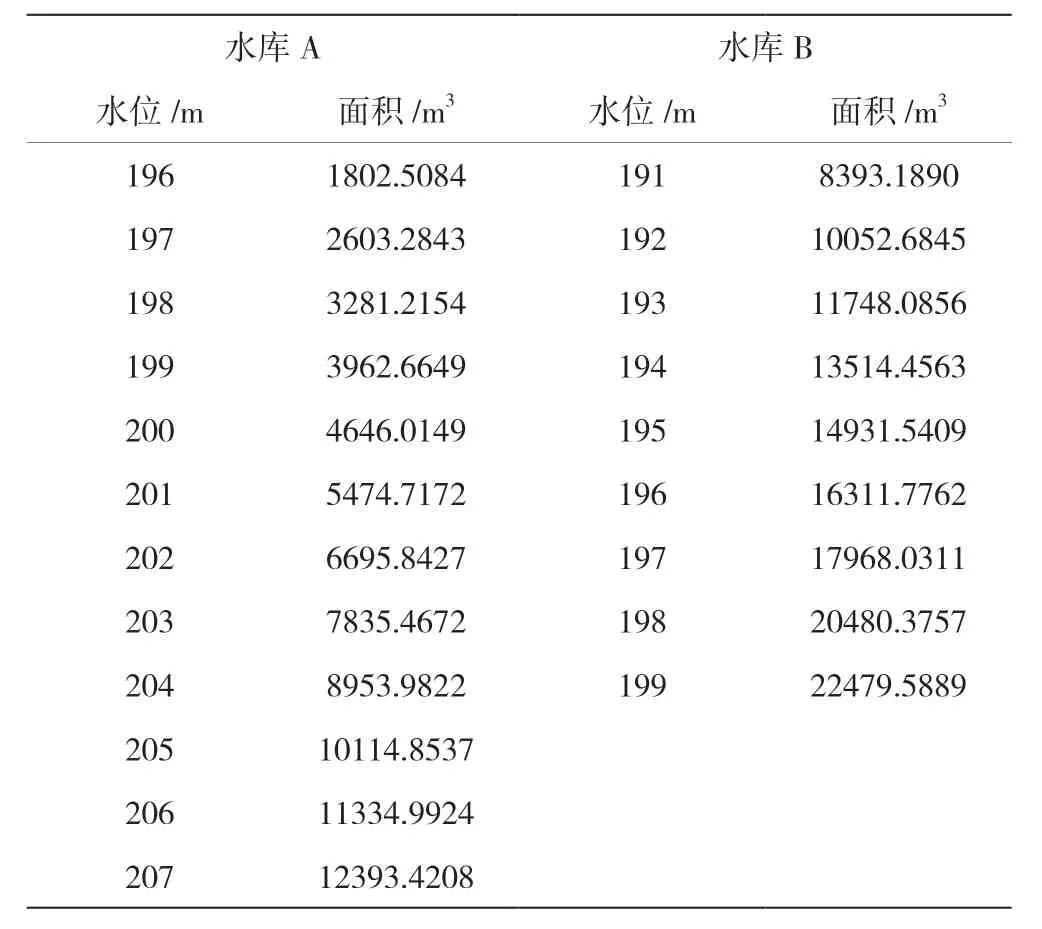
表1 两水库高程、面积关系

1.2 方法

1.2.1 断面法

断面法是沿河道布设一系列垂直于河道的横断面,将河道分割为n段,计算出每个横断面的面积S,根据相邻两断面的面积及间距d,算出每相邻两断面间的体积,然后各体积求和,得出该处水域的库容量。测量中断面法常用的库容计算公式有2 种: 梯形公式和截锥公式[1]。

梯形公式,又称为一般计算公式,具体公式为：

截锥公式,又称为严密计算公式,具体公式为：

式中：V为库容,m3；di为第个断面到第i+1 个断面的间距,m；n为分段个数；Si为第i个断面的面积,m2。

本文选用截锥公式作为基本组进行计算,取di=1。

1.2.2 ArcGIS 方法

在ArcGIS 软件中,利用等高线数据建立不规则三角网,再根据三维地表模型（TIN）生成DEM,利用DEM 法计算给定高程下的水库库容[7]。计算过程为：将已有等高线模型导入ArcGIS 中,生成相应线型模型。选中模型,将其Polyline导出为Shapefile 格式,将导出的Shapefile 格式模型导入图层中,选中改模型,通过ArcToolbox 菜单栏中3D Analyst 工具的数据管理选项,创建TIN,其中,将高程字段设为Elevation格式,生成TIN 模型。将生成的TIN 模型通过转换命令中的TIN 转栅格命令转换为栅格模型,方法选用NATURAL_NEIGHBORS,采样距离选用CELLSIZE 1,Z 因子保持默认为1,通过计算生成相应模型后,通过表面体积命令,参考平面选为BELOW,输入所需计算高程即可得出相应库容。

1.2.3 Global Mapper 方法

将水库A 等高线模型导入Global Mapper 中,在菜单栏的分析命令中,通过3D 矢量创建高程网格,根据所需计算水位高程,在AutoCAD 2021 软件中截取相应高程的等高线,保持其x、y轴坐标不变,将其导入Global Mapper 中,通过3D 矢量创建高程网格。通过工具菜单栏的配置选项,对单位尺寸及比例尺进行调整,在菜单栏的分析命令中使用测量地表间的体积命令,在第一个命令栏中选中相应高程面,第二个命令栏中选中地形模型,单位设置为cubic meters 确认后即可得出结果,重复以上步骤可计算出各水位库容。

1.2.4 3d Max 方法

3d Max 拥有强大的建模、材质和渲染功能[8-9],在实际应用中,3d Max 能够直观且真实地展现现实世界,帮助人们获得更加立体的景物观感[10]。使用3d Max 进行水库地形建模,通过其内置算法进行计算,可以直观地展示水位变化过程。本文通过3d Max 软件中块体之间的差集计算,得出相应库容水体体积。

以水库A 计算过程进行说明：为减小模型计算量,提高模型运算速度,通过AutoCAD 2021 软件截取所需计算的上水库部分等高线模型,将其导入3d Max 中,通过单位转换后可得到1∶1 的现场模型。

通过复合对象命令生成地形（图1）,通过标准基本体菜单栏中的平面命令创建平面,根据所需精度对平面进行网格划分,划分网格数量越多,生成模型精度越高,但对电脑配置要求也越高,本次模型使用100×100 进行网格划分,使创建平面模型在顶视图上包含图1（a）模型,且前视图中平面最低点在图1（a）模型最高点之上。

图1 水库A 地形模型

以所建平面为基础,对其使用一致命令,拾取包裹通过复合对象命令所生成的地形,使网格规整化,便于后续数据处理。生成规程网格后,将原有的不规则地形网格删除,选中规则网格,通过修改列表使其转化为可编辑多边形,选中生成多边形边界,通过挤出命令,将其边界挤出至前视图模型最低点之下,通过封口命令使挤出边界封口,将片状模型转化为实体模型。创建新的实体结构当作水体,使其涵盖于模型顶视图内,又使其包含所需计算地形轮廓（图2）。将其底边高程与所需计算起始高程196 m 保持一致,通过对其高度的改变模拟库区水位高程变化。

图2 水库A 两实体模型图

通过复合对象菜单栏中的布尔命令,截取两个模型实体间的差集,使用测量命令得出相应体积。

2 结果分析

本文以传统库容计算方法截锥法作为基本组,以ArcGIS、Global Mapper 与3d Max 作为对照组进行计算分析,同水库A 计算过程,可对水库B 进行计算,得出通过4 种方式计算出的水库库容的各结果。为分析各软件计算结果的精度与正确性,将各软件计算结果与传统算法计算结果通过以下公式进行计算：

计算得出结果见表2、表3。

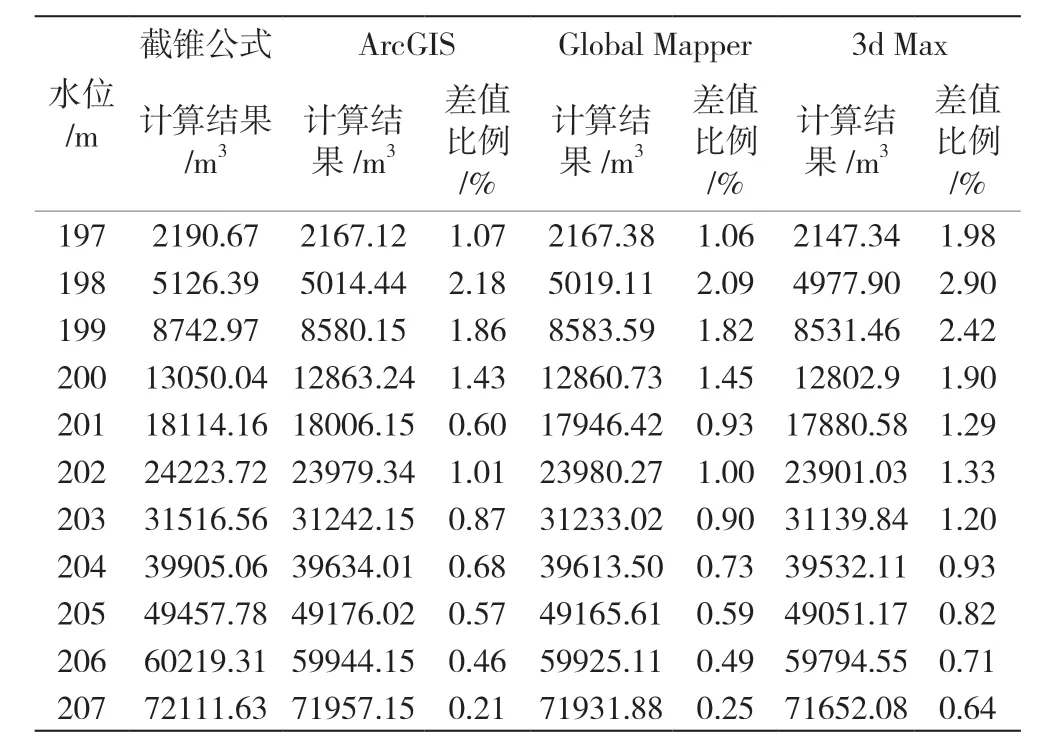
表2 水库A 各方法计算库容结果

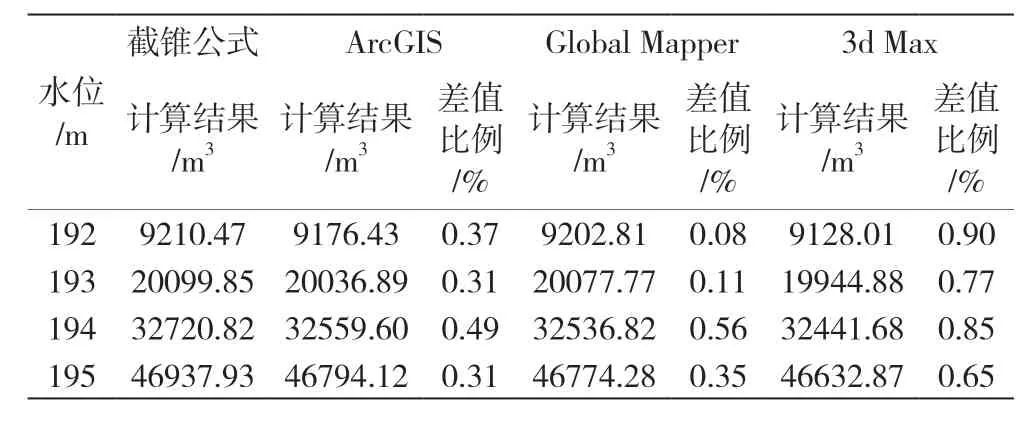
表3 水库B 各方法计算库容结果

根据水利设计、水库管理及测量单位要求,库容计算差值需控制在2.5%以内[11],由表可知各算法在两水库计算中所得出的总库容误差均完全符合要求,其中水库A 中ArcGIS 平均差值比例为0.99%,Global Mapper 平均差值比例为1.03%,3d Max 平均差值比例为1.47%,水库B 中ArcGIS 平均差值比例为0.22%,Global Mapper 平均差值比例为0.23%,3d Max 平均差值比例为0.51%。

三种软件的计算方法对比于传统计算方法,均存在差值比例随水库水位增高,断面面积增大而减小的趋势（图3（a）、图3（b））。为进一步证明该趋势,以水库A 为例,取1 m 作为相邻两断面的间距,计算出各方法中,每相邻两断面间的体积,将通过软件计算结果的各相邻断面体积分别对传统方法所计算出的结果做差值比较,计算过程不再赘述,计算结果见图3（c）。

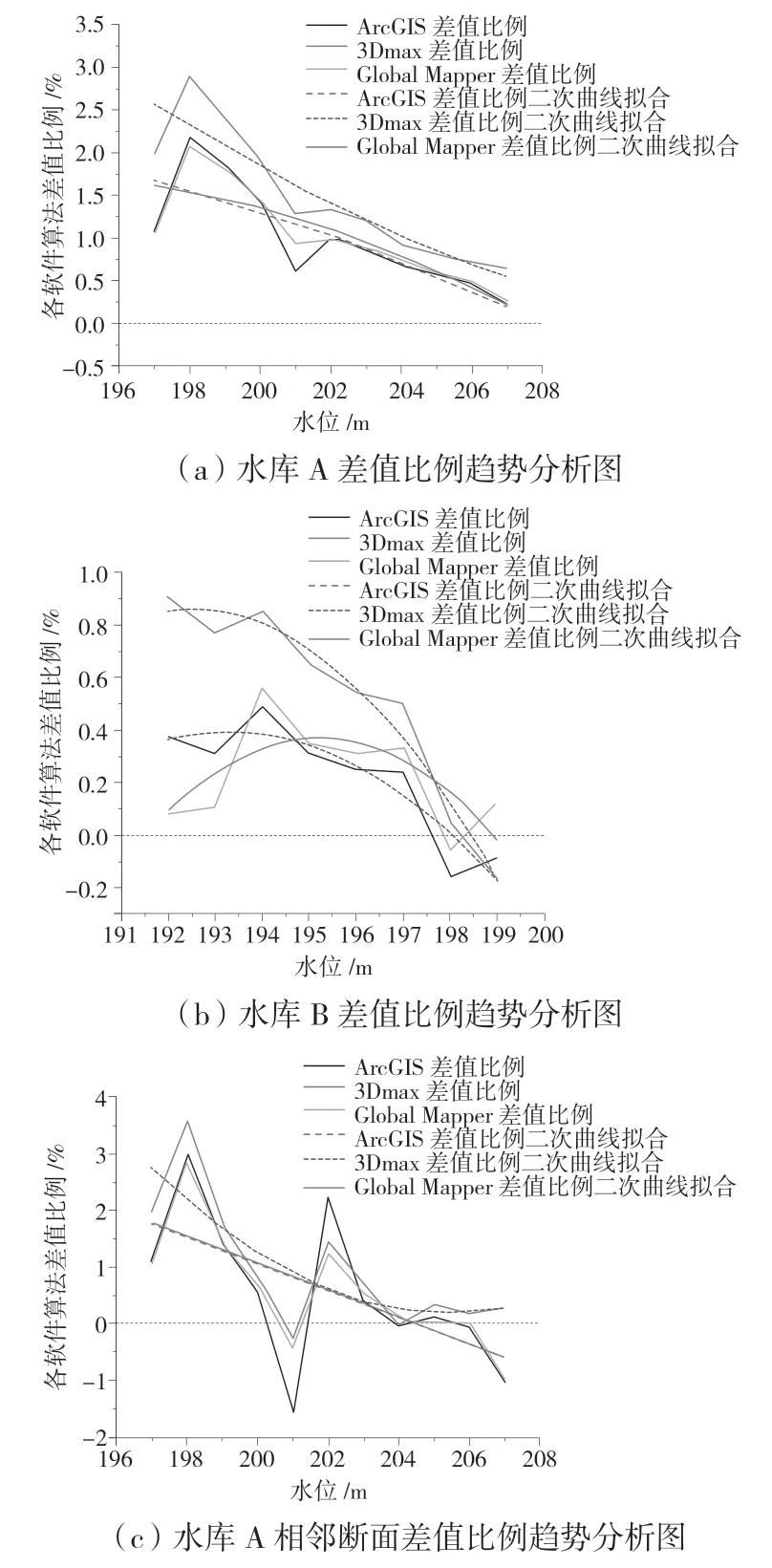
图3 趋势分析图

由图3 可知,本次研究的两水库通过软件计算所得数据的差值比例随着水位变化虽有所波动,但总体趋势为随着水位的提升其差值比例愈加趋近于0,存在差值比例随水库水位增高而减小的趋势,结果表明：随着水库库容的增加,各软件计算结果的精度也随之增加。

3 结论

（1）计算结果表明,ArcGIS、Global Mapper、3d Max 计算结果完全符合实际的工程应用需求,三种软件均可为水库库容计算提供新的参考方向。

（2）三种软件的计算方法对比于传统计算方法,均存在差值比例随水库水位增高,断面面积增大而减小的趋势。故推测,对于低水位情况,实测地形图测量的相对点密度较低,从而使等高线模型较为粗糙,导致软件与传统方法的计算结果差异相对较大,进而推测,对于库容越大的水库,三维软件计算误差越小。由于条件所限,本次研究未对中、大型水库进行计算,以上推理有待后续验证。

（3）3d Max 模型在计算过程中摆脱传统的数据分析与公式计算模式,直观地展示水库的地形条件,相比ArcGIS 与Global Mapper,其优势体现在可以很好地观测各水位淹没地形的变化过程,在水库有降等或升等的施工需求时,为土方开挖或回填位置提供参考。