喷水引纬机构动态特性对自由射流的影响
袁汝旺,孙英栋
(1.天津工业大学 机械工程学院,天津 300387; 2.天津工业大学 天津市现代机电装备重点实验室,天津 300387)
喷水引纬织机最早由V.Svaty开发并生产[1]。多年来随着市场需求的不断扩大,如今喷水织机正向高幅宽、高入纬率的方向发展。而水射流初始段最大距离与纬纱所受射流牵引力的大小直接决定了引纬质量的好坏,因此针对喷水引纬机构动态特性对射流影响的研究很有必要。
在喷水织机引纬机构动态特性的研究上,李克让等[2-4]通过联立功能原理求解得到了柱塞运动方程并分析了不同参数对织造的影响,Josef等[5]精确建立了含沿途阻力损失的柱塞运动方程;在水射流距离的研究上,文献[6-8]研究得到喷射长度、射流破碎位置与射流初始条件之间的关系,Zhan等[9]得出流速是射流破碎主要条件的结论,万云霞等[10]拟合了射流破碎长度随雷诺数变化规律;在射流对纬纱牵引作用的研究上,徐存强等[11]计算了不同气流纬纱相对速度时摩擦因数的变化。路翔飞等[12]、Belforte等[13]使用Fluent对射流流场中纬纱所受牵引力进行了仿真模拟;周浩邦[14]对不同截面形状喷嘴对中心轴线流速及牵引力进行了数值模拟。
本文从满足不同织机幅宽的需求出发,建立引纬机构动力学模型,分析了不同弹簧刚度系数与弹簧最大压缩量条件下喷水引纬机构动态特性的变化情况,并进一步计算了水射流初始段最大距离与射流对纬纱的牵引力,以期为不同织机幅宽需求下系统参数的选择提供理论依据与参考。
1 引纬原理与射流分析
1.1 引纬原理
喷水引纬机构通常是由凸轮与摇杆滑块机构串联的形式组成,图1为喷水引纬机构示意图。凸轮升程时柱塞左行挤压弹簧,在此过程中柱塞泵经进水阀执行吸水操作;凸轮回程时柱塞在弹簧的作用下迅速向右运动执行喷水操作,同时储纬器开启,此时水流通过喷嘴的整流充分作用于纬纱表面,纬纱受到射流牵引力的作用由静止开始加速穿过梭口,完成引纬动作。
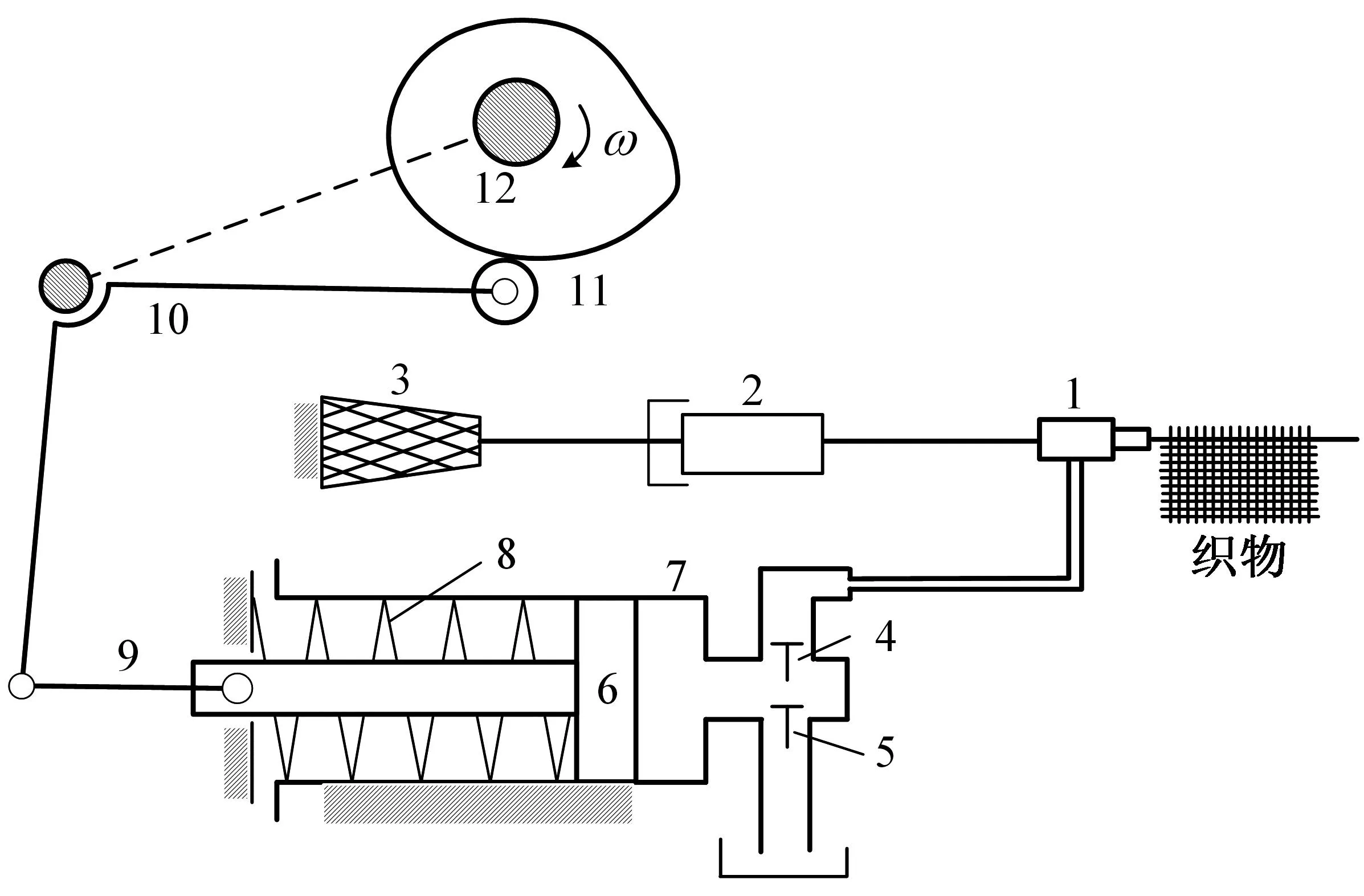
1—喷嘴; 2—储纬器;3—纱包;4—出水阀;5—进水阀;6—柱塞;7—泵缸;8—弹簧;9—连杆;10—角型杠杆;11—滚子从动件;12—凸轮。图1 引纬机构简图Fig.1 Schematic diagram of the weft insertion mechanism
1.2 射流分析
图2示出喷嘴射出水流在梭口中的飞行过程,水流在梭口中分别经历了以下3个区域:连续流体段(初始段)LA、单独流体段(基本段)LB、水雾。图2中v为喷嘴出口流速,vz为水射流截面开始扩散后其轴心位置的水流速度。

图2 水射流结构示意图Fig.2 Schematic diagram of the structure of the water jet
由图2可知,射流初始段截面为近似的圆形,轴心线上流速一致且等于喷嘴出口流速,具有比较高的能量密度,此阶段纬纱由静止开始加速,与水流速度的差值最大,纬纱所受的牵引力也是最大的;由于卷吸和掺混现象,射流基本段截面开始不断扩大,轴心速度逐渐下降,但射流仍未分离[15]。雾化段便失去了对纬纱的牵引作用。为满足不同织机幅宽的引纬需求,需要建立射流初始段最大距离、纬纱所受射流牵引力与不同参数条件下机构动态特性之间的数值模型,并进行分析研究。
2 数学模型
2.1 柱塞动力学模型
柱塞在运动过程中受到惯性力Fg、弹簧回复力FT、水的压力FS以及摩擦阻力Ff的作用,动力学方程如下:
Fg-FT+FS+Ff=0
(1)
其中FS、Fg、FT的表达式如下:
(2)
式中:m为柱塞组件质量,kg;x为柱塞位移,m;k为弹簧刚度系数,N/m;x0为弹簧最大压缩量,m;P为管内水压,Pa;S为柱塞截面积,m2。
图3为柱塞喷射系统示意图,管内水压P可通过流体的伯努利方程求得。同时为方便计算,做如下假设:柱塞泵体配合为理想状态;流体运动遵循伯努利原理;忽略水的可压缩性;忽略沿途压力损失。
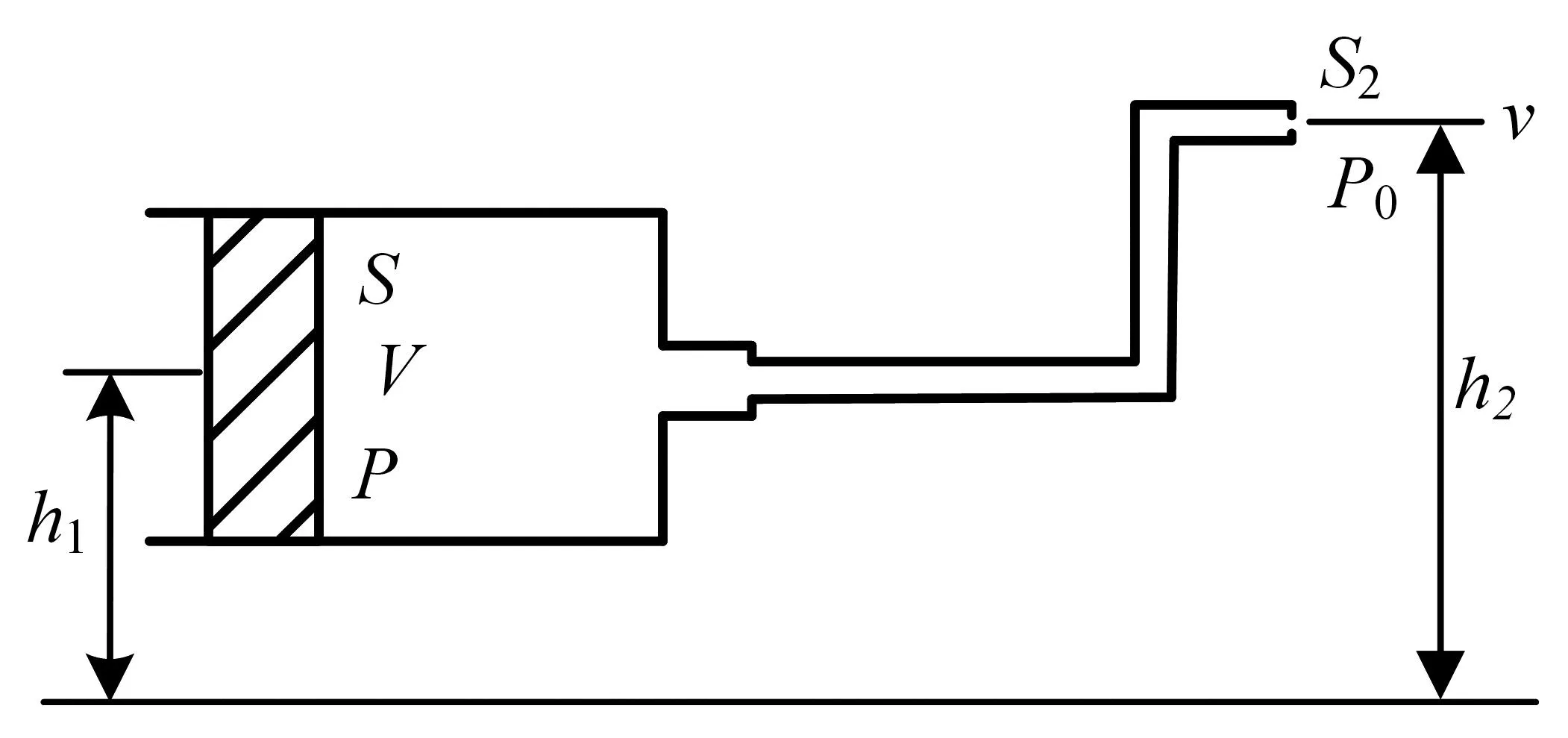
图3 柱塞喷射系统示意图Fig.3 Schematic diagram of plunger injection system
(3)
式中:P0为大气压,Pa;ρ为流体密度,kg/m3;g为重力加速度,m/s2;h1、h2分别为为柱塞与喷嘴的离地高度,m;V为柱塞运动速度,m/s;v为射流速度,m/s。
喷嘴射流速度可通过液体连续性原理求得:
v=SV/CS2
(4)
式中:S2为喷嘴出口截面积,m2;C为流量系数,一般取0.95~1。
通过式(4),管内水压P可进一步表示为:
(5)
将式(5)代入式(1),则完整的柱塞动力学方程为:
(6)
利用高精度四阶Runge-Kutta(龙格-库塔)数值方法对此微分方程进行求解,便可得到取不同弹簧最大压缩量与弹簧刚度系数条件下柱塞动态特性随时间的变化规律,进而求得射流性能参数的数值。
通过柱塞系统的动力学方程可得到系统自由振动的固有频率ω:
(7)
系统的相对阻尼系数ξ:
(8)
式中:c为系统的黏性阻尼系数,N·s/m。
系统阻尼自由振动频率ωn:
(9)
系统阻尼自由振动周期T:
(10)
对应的凸轮最低转速n:
n=30/T
(11)
2.2 射流参数模型
喷水引纬采用的喷嘴截面通常为圆形,且射流速度很快,其流动状态为湍流。故在求解水射流初始段距离时,使用圆柱射流湍流状态下基于流体雷诺数的射流初始段距离经验公式进行近似求解:
(12)
式中:LA为射流初始段距离,mm;Re为雷诺数,一种用来表征流体流动情况的无量纲数;μ为流体黏性系数,Pa·S;d为喷嘴直径,m。
在引纬的初始阶段,纬纱完全处于被水流包裹的状态且为定速水流。在此过程中,水射流作用于纬纱上的牵引力Fy可用下式表示:
(13)
式中:u为纬纱的飞行速度,射流初始段通常取值为0.8v;d0为纬纱的直径,m;l为纬纱的长度,m;B为实验常数。
3 结果与讨论
利用动力学模型求解柱塞动态特性以及求解射流初始段最大距离与射流对纬纱牵引力时,相关射流组件参数见表1。

表1 射流组件参数Tab.1 Jet component parameters
3.1 柱塞运动特性
图4、5分别示出选择不同弹簧最大压缩量x0、弹簧刚度系数k时柱塞第1个运动周期内的位移x随时间的变化情况。

图4 不同最大压缩量时柱塞位移随时间的变化曲线Fig.4 Variation curve of plunger displacement with time at different maximum compression amounts
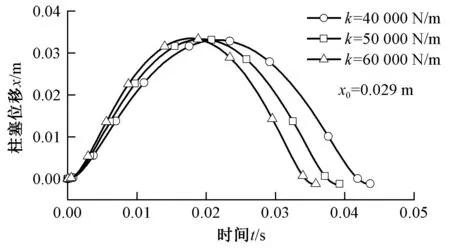
图5 不同弹簧刚度时柱塞位移随时间的变化曲线Fig.5 Variation curve of plunger displacement with time at different spring rates
表2、3分别示出不同弹簧最大压缩量x0与弹簧刚度系数k条件下柱塞喷射系统的阻尼自由振动周期T与对应主动凸轮的最低转速。
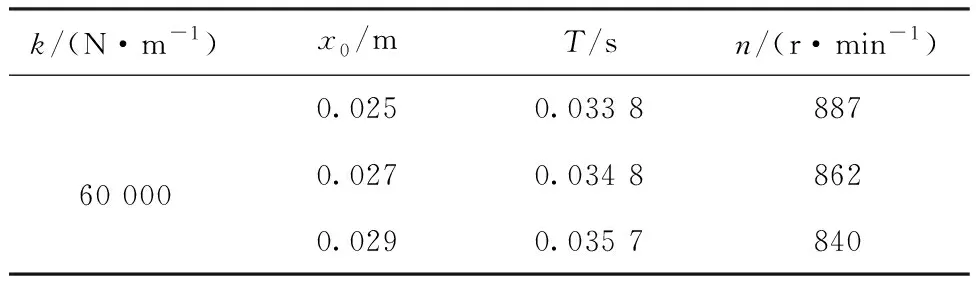
表2 不同最大压缩量对应的周期与转速Tab.2 Cycles and rotational speeds corresponding to different maximum compression amounts
结合图4、5与表2、3可以得出:弹簧刚度系数引起柱塞运动周期的变化非常明显。随着弹簧刚度系数的增大,柱塞运动周期变小,即柱塞在更短时间内便完成了射流动程,对应的系统最低转速应越大;而弹簧最大压缩量对柱塞运动周期影响的幅度很小,但是对柱塞位移的影响较大,在实际生产中可通过改变凸轮从动件最大动程来控制弹簧最大压缩量以实现每纬用水量的调节。
3.2 引纬凸轮设计
弹簧最大压缩量取0.029 mm时,根据相应机构尺寸,可求得凸轮摆动从动件最大动程H。进一步对凸轮机构进行设计,在运动规律的选择上:从外形尺寸最小、系统无量纲转矩最小角度考虑,在升程与回程皆采用等速运动规律[16],同时为防止交接处因加速度突变产生刚性冲击,在等速运动端两侧使用摆线函数进行修正。
根据不同弹簧刚度系数条件下确定的最低转速,图6示出凸轮回转1周摆动,从动件角位移随时间的变化情况。
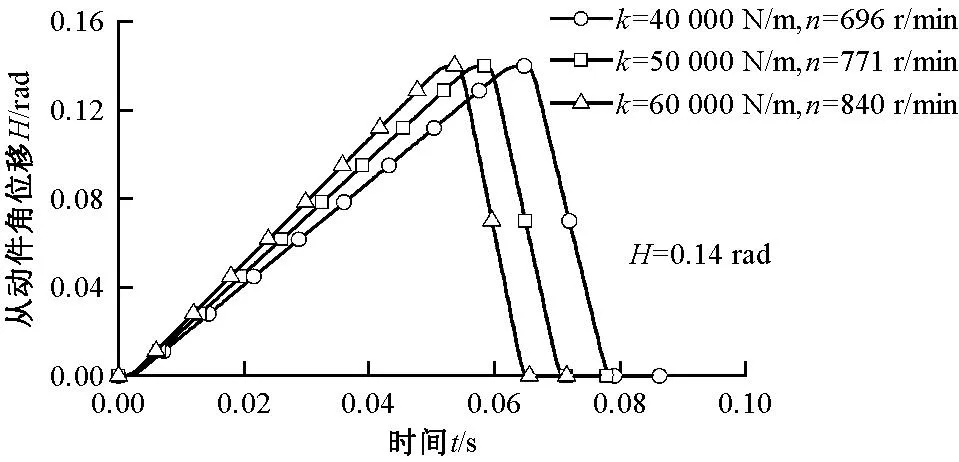
图6 从动件角位移随时间的变化曲线Fig.6 Angular displacement curve of the follower over time
由图6可知:不同转速条件下凸轮回转1周所用时间分别为0.086 21、0.077 82、0.071 43 s,回程运动角为90°,所用时间分别为0.021 6、0.019 5、0.017 9 s,与表3中柱塞喷射系统半周期近似相等,可有效减少柱塞在运动过程中因弹簧残余振动而导致的误吸水操作与系统振动。由此可知,本文中通过系统弹簧刚度系数确定凸轮最低转速的方法是合理的。相应的凸轮轮廓曲线如图7所示。
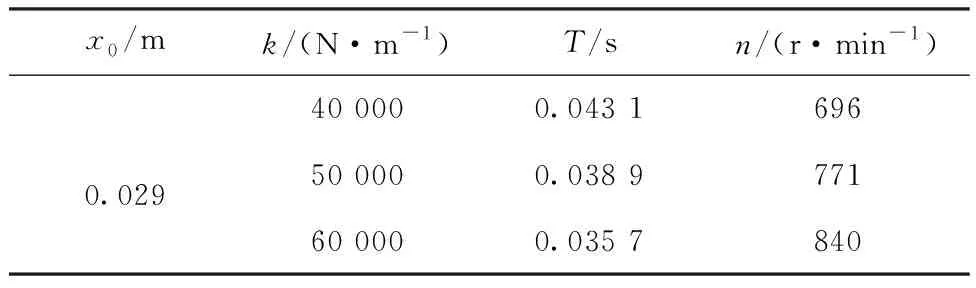
表3 不同弹簧刚度对应的周期与转速Tab.3 Cycle and speed corresponding to different spring rates
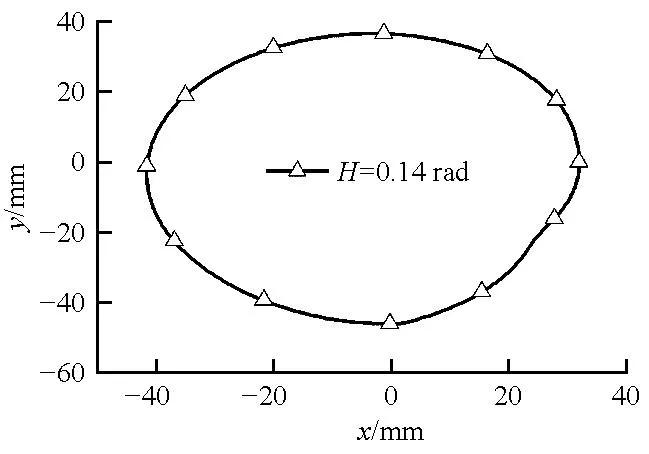
图7 凸轮轮廓曲线Fig.7 Cam profile curve
3.3 射流性能参数
图8、9分别示出选择不同弹簧最大压缩量x0、弹簧刚度系数k时柱塞第1个运动周期内,速度V随时间的变化情况。

图8 不同最大压缩量时柱塞速度随时间的变化曲线Fig.8 Curve of plunger velocity with time for different maximum compression amounts
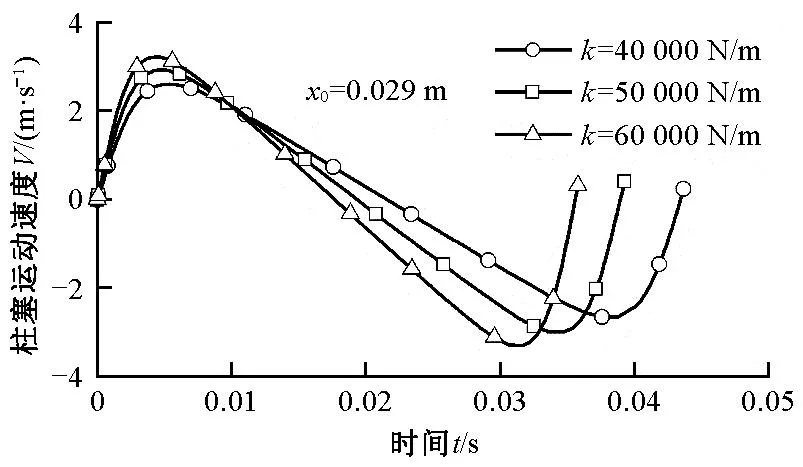
图9 不同弹簧刚度时柱塞速度随时间的变化曲线Fig.9 Variation curve of plunger velocity with time at different spring rates
在得到柱塞运动速度V随时间的变化规律后,取柱塞的射流动程(即柱塞运动周期的前半段),通过液体连续性原理可求得喷嘴出口的射流速度v。
图10、11分别示出在选取不同的弹簧最大压缩量x0以及弹簧刚度系数k时,射流速度随时间的变化情况。
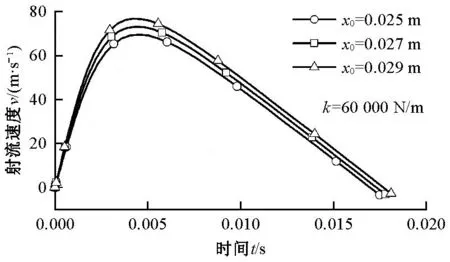
图10 不同最大压缩量时射流速度随时间的变化曲线Fig.10 Curve of jet velocity with time for different maximum compression
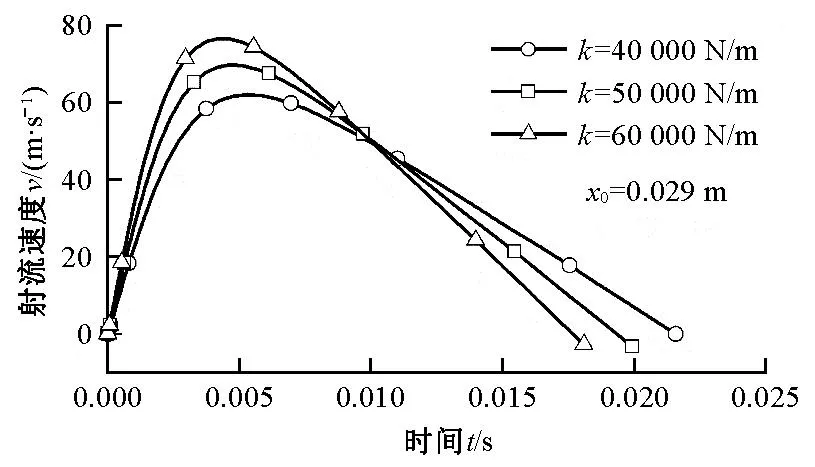
图11 不同弹簧刚度时射流速度随时间的变化曲线Fig.11 Curve of jet velocity with time at different spring rates
通过射流速度峰值vm,进一步求得初始段射流为定速流体时雷诺数Re、射流初始段最大距离LA与射流对纬纱的牵引力Fy随系统参数x0、k的变化情况,结果如表4、5所示。

表4 弹簧最大压缩量对射流性能参数的影响Tab.4 Effect of maximum spring compression on jet performance parameters
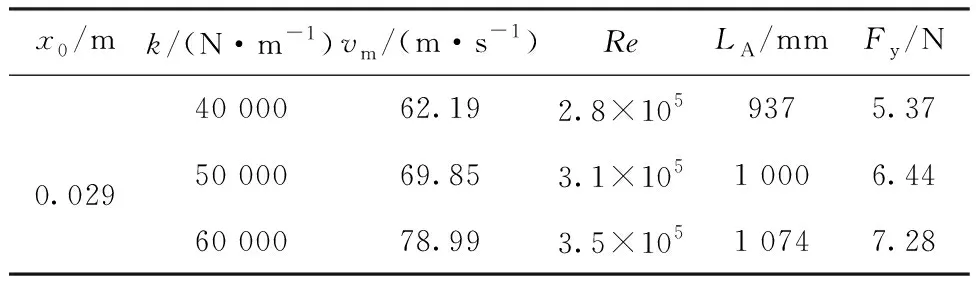
表5 弹簧刚度系数对射流性能参数的影响Tab.5 Effect of spring rate coefficient on jet performance parameters
结合图10、11与表4、5可以得出:随着弹簧刚度系数的增大,射流速度峰值变大,同时射流速度峰值出现的时间更早,在弹簧刚度系数每增大10 000 N/m时,其射流速度最大值vm、雷诺数Re、射流初始段最大距离LA、纬纱牵引力Fy的平均增幅分别为12.7%、12.7%、7.1%、11.75%;而弹簧最大压缩量的变化对射流速度峰值以及上述射流参数的影响幅度很小。故在引纬幅宽需求增大时应优先选择更大的弹簧刚度系数。
4 结 论
本文从不同喷水引纬织机幅宽的需求出发,联立伯努利与液体连续性方程建立了柱塞运动过程的动力学模型,分析了不同弹簧刚度系数与最大压缩量对柱塞的动态特性以及对喷嘴自由射流的影响。得到结论如下:
①随着弹簧刚度系数增加,喷水引纬系统阻尼自由振动周期减小,为了防止柱塞在运动过程中因弹簧残余振动而导致的误吸水操作与系统振动,凸轮最低转速应相应增加。
②弹簧刚度系数对射流雷诺数、初始段最大距离、纬纱所受射流牵引力等参数具有显著影响,当弹簧刚度增幅10 000 N/m时,射流雷诺数、初始段最大距离、纬纱所受射流牵引力平均增幅分别可达12.7%、7.1%、11.75%;而弹簧压缩量对上述变量的影响幅度很小。故在大幅宽织机需求下应首要考虑使用更大刚度系数的弹簧。

