基于两点模型的堆芯功率多目标保性能控制
刘雨昆,王俊玲,张玉衡
(核安全与仿真技术国防重点学科实验室,哈尔滨工程大学,哈尔滨 150001)
已随着现代能源行业的实际需要,核电机组在电网整体中的占比有所增加,这就要求核电机组具有随着电网负荷改变输出功率的能力[1].但是由于核反应堆是一个高度非线性的时变系统,在大范围内进行功率变动时,负荷跟踪的实现更加困难.由于目前大规模采用的PID控制方法难以满足实际需要,因此现在一些先进的控制方法被引入了核反应堆控制技术当中[2],包括:现代控制理论中的自适应控制技术[3]、变结构控制技术[4]、最优控制技术等[5];智能控制理论中的模糊控制技术、神经网络控制技术等以及多种控制方法结合[6]的控制技术等.上述方法均在所设定的工况下获得了较为理想的控制效果,但是由于核电堆芯的重要性以及现在所设计的控制器在实际工程中还存在着实用价值不足等问题[7],因此仍需要继续反应堆堆芯控制进行研究.
此外,现有的研究在设计反应堆堆芯控制器时,大多数都以反应堆点堆模型为基础进行设计[8],这一模型无法考虑由于轴向氙震荡等原因引起的堆芯轴向的功率分布变化.但是实际工程中轴向功率:ΔI=(nrt-nrb)/(nrt+nrb)的分布是影响堆芯安全运行的重要因素[9].因此需要采用多点模型设计控制器,将轴向功率偏差控制作为一个控制目标,使偏差值在全工况下低于阈值[10].
鉴于保性能控制方法可以在一定范围内寻找一个控制策略使系统进行状态转变时获得良好的性能指标,据此可设计有效实现负荷跟踪控制目标的控制器[11].但是在堆芯功率模型中,部分变量会随着时间或工况变化,一般设计过程中会将这一部分参数假设为定值,但是这一设计方式不利于适应压水堆堆芯的时变性,因此在设计保性能控制器时,将保性能控制器与线性参数变化(LPV)控制方法相结合,以实现理想的控制性能.
本文基于两点堆芯18阶堆芯增广模型进行控制器设计,采用LQR-LPV方法通过调节权值矩阵等参数,实现保性能控制指标的同时获得较强的抗时变参数能力,满足各种工况下负荷跟踪控制及轴向功率偏差控制的需要.采用16阶堆芯两点模型进行模拟,验证设计的多目标控制器满足负荷跟踪和轴向功率分布控制需要.
1 两点模型建模
核反应堆功率系统模型由一组非线性模型组成,两点堆芯模型中将堆芯分为上下两部分进行建模,并通过一个耦合系数将上下部分参数进行联系.
所得到的16阶堆芯两点模型见式(1),其中:下角标t为堆芯上半部分,b为堆芯下半部分[12];模型中所采用相关参数值见表1[13].
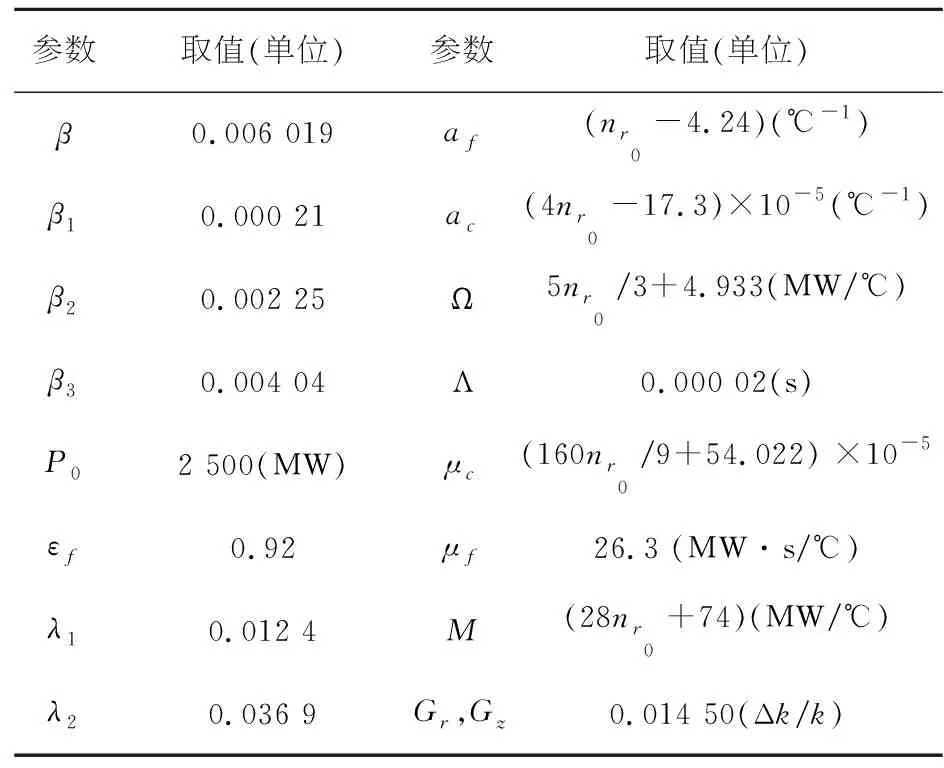
表1 模型中相关参数值
(1)
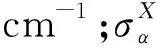
其中:D为中子扩散系数;v为热中子速度;S为两半面之间的界面的面积;d为堆芯的上半部与下半部之间的距离;V为堆芯一半的体积.
在功率平衡点nrt0,nrb0处对模型进行线性化处理,由于反应堆控制时一般采用冷却剂入口温度恒定策略,因此δTe=Te-Te0=0,氙碘浓度取相对值以降低矩阵的刚性,得到16阶状态空间模型如下:
(2)
其中状态变量为:
x(t)=[δnrtδcrt1δcrt2δcrt3δnrbδcrb1δcrb2δcrb3δTfδToδIrtδIrbδXrtδXrbδρtδρb]T
系统输入为:u(t)=[Zr1Tr2]T;
系统输出:y(t)=[δnrΔI′]T;其中ΔI′为轴向功率偏差简化值ΔI′=δnrt-δnrb+ΔI′0,系统矩阵为:
系统矩阵B、C以及A的具体构成如下:
A1=
求解时设置nrd为预期功率,设置ΔI′d为轴向功率偏差预期值ΔId=AOaim×nr,ΔI′d=ΔId×nr.其中:AOaim为满功率状态下轴向功率偏差的预期值.根据这一性能需要构建增广状态空间模型,增广状态向量为:
上述两种跟踪量计算方法如下:
(3)
保性能控制器在设计过程中通过调整各个状态量和控制输出量的增益权值,实现各种预期性能.本文将上述两个跟踪变量所对应的权值调整至较大水平,即可实现负荷跟踪控制和轴向功率分布多目标控制.
增广后得到的状态空间模型和系统矩阵如下:
(4)
其中:dr=[nrdΔI′d]T,本文在实际进行控制器设计求解时,取nrd=0,ΔI′r=0.本文基于式(4)增广模型和表1中参数进行控制器设计.
2 核反应堆LQR-LPV多目标控制器设计
针对式(5)所示的模型,设计对应的保性能控制器成本函数:
(5)
其中:Q和R分别为状态量和控制输入的成本矩阵,tf为控制的终止时间.根据系统(4)和式(5)可以得到引理1[14].
引理1对于系统(4)和保成本成本函数(5),若存在一个正定矩阵P和向量K使得如下的不等式成立,则求解得到K为系统(3)的LQR保性能控制增益.
(A+BK)TP+P(A+BK)+Q+KTRK<0
(6)
由于式(6)中存在交叉相乘项,无法直接求解,因此根据式(8)和Schur定理[14]可以得到定理2.
定理1 对于堆芯增广模型(4),存在一个保性能控制器,当且仅当存在一个正定矩阵X=P-1及向量W使得如下的不等式组成立:
(7)
(8)
(9)
将不等式(8)带入式(9)中可以得到:
(10)
由此,结合李雅普诺夫稳定性理论,可证明闭环系统(9)渐进稳定.进一步基于LQR控制器设计能够适应堆芯功率模型时变性的LQR-LPV多目标控制器.堆芯功率模型(4)中,在进行堆芯功率调节时,存在部分参数会随着堆芯中子相对密度nr,nrt,nrb而变化,在实际进行控制调节时,这一部分参数会影响到控制性能,因此将堆芯功率模型中含有相关参数的部分分离出来,设m为堆芯相对功率值:
(11)
按求解LQR控制器的思路对LQR-LPV控制器进行求解,可以得到如下的定理:
定理2:设有权值矩阵Q、R,若存在正定矩阵X和向量组Wi(i=0,1,2,3),若满足如下所示的线性矩阵不等式组:
W′+W0+r1W1+r2W2+r3W3
(12)
若方程组有可行解, 可以求解得到Ki=WiX-1,进一步得到LQR-LPV控制增益:
K=K0+r1K1+r2K2+r3K3
(13)
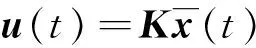
3 数值仿真
对设计得到的LPV-LQR多目标控制器进行仿真模拟,并与LQR保性能控制器进行对比.
设置权值矩阵:
Q=diag[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,200,200]
T=diag[200,200];
设置控制棒棒速的变化区间:-0.02 m/s≤Zr≤0.02 m/s;
设定轴向功率偏差基准值:
ΔIaim=AOaim×nr,AOmax=-0.1, ΔI′d=ΔIaimnr

工况A(堆芯功率阶跃变化):仿真时间200 s,初始功率水平为40%FP,功率预期值在运行至50 s时阶跃变化值60%FP,之后稳定在60FP这一功率水平.
工况B(堆芯功率线性变化):仿真时间600 s,初始功率水平为40%,功率预期值在运行至100 s时以0.05%FP/s的速度线性上升至50%FP,维持这一功率水平至400 s后,功率预期值以0.05FP/s的速度线性下降至40%FP,维持这一功率水平直至模拟结束.
两种工况下的模拟结果见图1~6,从图1和图4的模拟结果中可以看出,LQR-LPV控制器跟踪性优于保性能控制器,LQR-LPV控制器响应速度更快且调节时间更短,负荷跟踪性能更加优秀.从图2和图5中可以明显的发现,LQR-LPV控制器相对于保性能控制器能够更快速的调节堆芯功率轴向功率偏差,有抖震出现但是震荡范围处于限制范围之内.
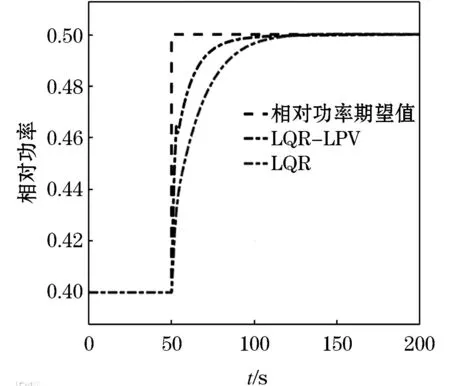
图1 工况A相对功率变化Figure 1 Change in relative power under condition A

图2 工况A轴向功率偏差变化Figure 2 Changes in axial power deviation under operating condition A
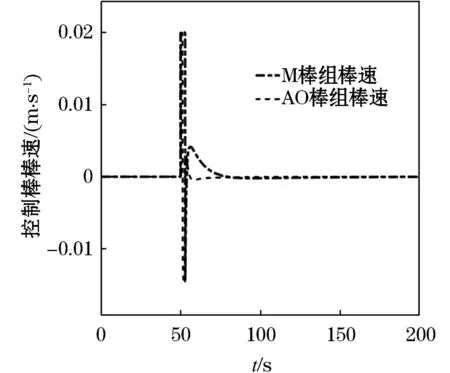
图3 工况A下控制棒棒速Figure 3 Control rod speed under condition A

图4 工况B堆芯相对功率变化Figure 4 Change in relative power under condition B

图5 工况B轴向功率偏差变化Figure 5 Changes in axial power deviation under operating condition B
从图3和图6的仿真结果表明:在两种工况下,控制棒棒速在调节过程中均未超过限制棒速.LQR-LPV控制器调节速度更快,超调量更小,在受到干扰后能够更有效的做出调整,有着优秀的轴向功率分布控制能力.综合上述仿真结果进行分析可以发现,由于LPV-LQR多目标控制器相对于保性能控制器能够更好的适应堆芯功率模型的时变性,因此能够获得更好的控制性能.
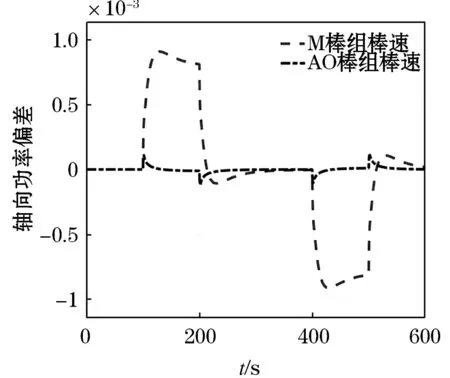
图6 工况B控制棒棒速Figure 6 Control rod speed under condition B

