基于足底压力分布的下肢步态识别方法*

颜兵兵，王 强，宋佳宝，殷宝麟，胡春玉

（佳木斯大学 机械工程学院，黑龙江 佳木斯 154007）

0 引言

人与外界环境的交互是多模态的，可以通过视觉、味觉、嗅觉、听觉和触觉获取外界信息，利用大脑对获取的信息进行处理，用以理解外部世界［1］。针对助力外骨骼机器人，良好的下肢步态感知能力是人与外骨骼机器之间融合度评价的关键指标，也是人机共融领域［2］的热点问题。

杨敏等人［3］利用足底压力采集装置对行走、跑步和下蹲3种步态信号进行采集并用于人体步态分析。魏鹏娜等人［4］采集脑电波（electroencephalogram，EEG）信号和表面肌电（surface electromyography，sEMG）信号，采用K 最近邻（K-nearest neighbor，KNN）算法和核支持向量机（kernel SVM，KSVM）算法进行下肢步态感知。刘薛勤等人［5］采集足底周期性运动步态的压力数据，利用支持向量机（SVM）对下肢步态数据进行分类，由此感知下肢步态。贾晓辉等人［6］提出了一种基于模型映射和卷积神经网络（convolutional neural network，CNN）区分人体步态相位的方法，并对不同的步态进行识别，可准确感知人体运动意图。Ivanov K等人［7］使用带有传感器鞋垫来收集59 名户外行走的运动数据，利用CNN对这些数据进行身份识别，平均识别准确度为93.3%。刘今越等人［8］将压力传感器和惯性测量单元（inertial measurement unit，IMU）采集的数据融合为足部运动数据，搭建CNN 识别行走步态相位，平均识别准确率为94.58%。

基于前人研究结果可将下肢步态感知的实质理解为：通过不同的感知方式获取下肢运动信息，并采用不同的神经网络方法感知不同的下肢步态。可以看出，下肢步态感知方式可归纳为生物信号感知、惯性感知与足底压力感知。其中，生物信号sEMG的采集易受外界环境的干扰；惯性传感器佩戴位置的差异性大，均会降低下肢步态感知的效率与精度。相对于上述2 种感知方式，基于足底压力感知的步态感知方法具有良好的灵敏度与测量精度。

基于此，本文以足底压力分布为研究对象，构建足底压力分布采集装置，采用多元线性回归法将足底压力分布数据转换为地面反作用力，并基于CNN分类算法进行下肢不同步态的感知。

1 足底压力分布采集

1.1 足底压力分布采集装置

足底压力分布数据是下肢步态感知的数据基础，鉴于压力传感器的数量大小和位置分布方案会直接影响足底压力采集装置的采集性能［9］，本文拟定8 只压力薄膜传感器的位置分布方案（如图1）：在足后跟的内外侧分布3个传感器节点（M3，M4，M5）；在足中部外侧安装2 个传感器节点（M7，M8）；在足前部安装3个传感器节点（M1，M2，M6）。

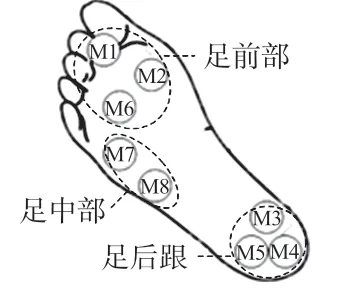
图1 压力传感器的位置分布

本文鉴于成年人站立时的最大足底压力为（1.28 ±0.33）kg／cm2，运动时的最大足底压力为（2.96 ±0.66）kg／cm2，且站立与运动时足底与地面最小接触面积为2 cm2［10］。本文采用柔性薄膜压力传感器ZNX—01，设计出一种可穿戴在鞋内的足底压力采集装置，装置实物及其接线图如图2所示。

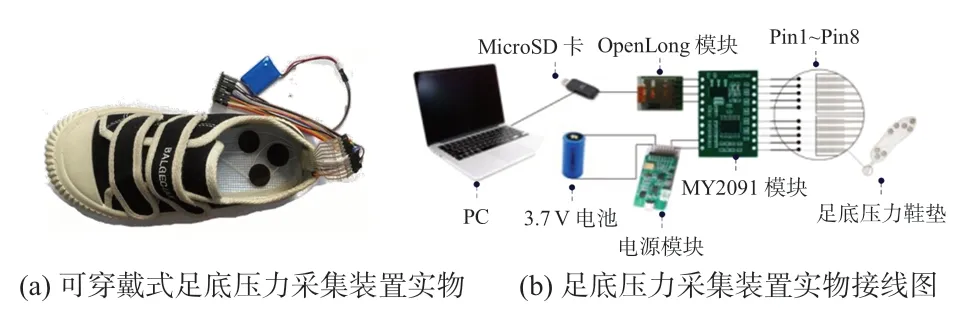
图2 足底压力采集装置

1.2 足底压力分布采集试验

邀请身体健康、下肢关节骨骼正常的人员（身高为178 cm，体重为85 kg）为试验采集对象，开展平地行走（行走速度为1.2 m／s）足底压力分布数据的采集试验，试验结果如图3所示。其中，M1—M8分别为足底压力采集装置中8只压力传感器采集的压力数据。

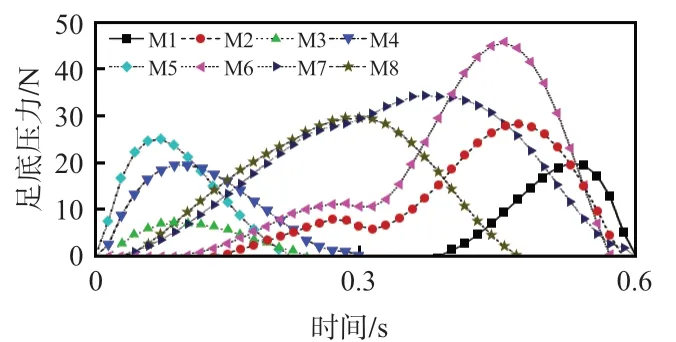
图3 平地行走时足底各区域压力曲线

由图3可知，平地行走一个步态周期内足底压力变化顺序依次为：触地期时足后跟与地面接触，足后跟区域（M3，M4，M5）受压逐渐增大，随着运动进入承重期，足后跟区压力逐渐变小，足中前部区域（M2，M6）与地面接触，足底压力随足中前部区域压力增大而逐渐增大。当运动进入站立期，足后跟区压力下降，足中部区域（M7，M8）受压明显增强。离地期时足前部区域（M1）受力达到峰值，足底其他区域压力减小或为零。其运动过程与受力顺序符合足底生物力学分析结果［10，11］，可用于地面反作用力预测。

2 地面反作用力预测

2.1 地面反作用力预测模型

借助足底压力采集装置虽能采集不同步态足底压力分布数据，但若要感知下肢步态，则需获取足底整体压力数据（或称地面反作用力），而非分布压力数据。因此，本文基于多元线性回归法构建足底压力分布数据X 与地面反作用力Y之间的关系模型

式中 α为回归系数。若能确定平地行走、平地慢跑和坡路行走3个步态的回归系数α1，α2和α3；再通过前一节搭建的足底压力分布采集装置采集3个步态足底压力分布数据X1，X2和X3；即可通过式（1）获得地面反作用力Y。

为获取回归系数α，首先借助文献［12］中经验公式（见式（2））分别获取上述3 个步态地面反作用力经验值

式中 m为人体质量，β为支撑期占比，q为凹陷系数，p为峰值对称参数，T为步态周期，t为时间；不同步态时，β，q和p取值不同［13，14］；基于式（2）可获得地面反作用力经验值

式中 y，y′和y″分别为平地行走、平地慢跑和坡路行走的经验值；n为采样样本数。

然后利用足底压力分布采集装置分别采集3个步态足底压力分布数据X1，X2和X3

式中 x，x′和x″分别为平地行走、平地慢跑和坡路行走足底压力分布的采样数据。

最后利用式（5）计算出3 个步态的线性回归方程的回归系数

将式（4）和式（5）代入式（1）中，即可获得平地行走、平地慢跑和坡路行走3个步态的地面反作用力的预测模型

2.2 地面反作用力预测试验

首先，针对平地行走（1.2 m／s）、平地慢跑（2.2 m／s）和坡路行走（坡度为10.8°，1.2 m／s）3 个不同步态，分别采集试验者在平坦地面上20 组足底压力分布数据；其次，将表1设定的参数［13，14］代入式（2）中计算出地面反作用力经验值；然后，选取10 组足底压力分布数据进行线性回归试验分析，并将调整后拟合度指标（R2）最高的一组确定为足底压力分布数据；最终，由式（5）求得上述3个步态对应的回归系数α1，α2和α3

表1 不同步态地面反作用力经验参数

以此确定该试验条件下3个步态的地面反作用力预测模型。基于此模型，从3个不同步态的20组数据中选择另外的10组足底压力分布数据进行地面反作用力预测获得预测值Y1，Y2和Y3，并与经验值进行对比。选取其中一组对比结果，如图4 所示。可以看出，3 个不同步态地面反作用力的预测值与经验值基本一致。

图4 不同步态地面反作用力预测值与经验值对比

引入归一化均方根误差（normalized root mean square error，NRMSE）作为误差评价指标，将预测值与经验值做误差对比分析，结果如图5所示。可以看出，3 个步态地面反作用力预测值与经验值的NRMSE均在4%～10%之间，平均误差分别为7.4%，7.7%和6.0%，预测结果均在工程应用的接受范围内［15］，满足后续步态感知的需求。

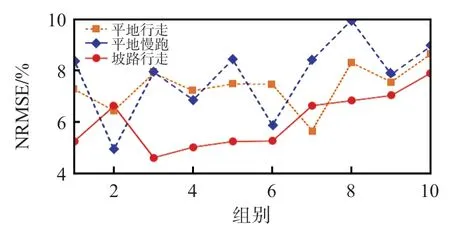
图5 地面反作用力预测值与试验值的NRMSE

3 下肢步态感知

3.1 下肢步态感知算法

平地行走、平地慢跑和坡路行走3 个步态的地面反作用力的变化趋势存在明显差异，可从上述3 个步态的地面反作用力原始数据中提取包括均值、标准差、均方根和最小值在内的特征值，再采用Mapminmax函数针对上述特征值进行归一化处理，以便得到用于CNN学习所用的训练与测试数据，最终获得下肢不同步态的分类结果，以此实现基于足底压力分布的下肢步态感知功能，具体流程如图6所示。

图6 基于足底压力分布的下肢步态感知流程

本文搭建的CNN架构（如图7）由卷积结构和分类器构成，其中卷积结构由2 个卷积（Con1，Con2）层、1 个最大池化（Maxpool）层和2个批归一化（Norm1，Norm2）层组成，分类器由1个全连接（FC）层和1个SoftMax层组成。

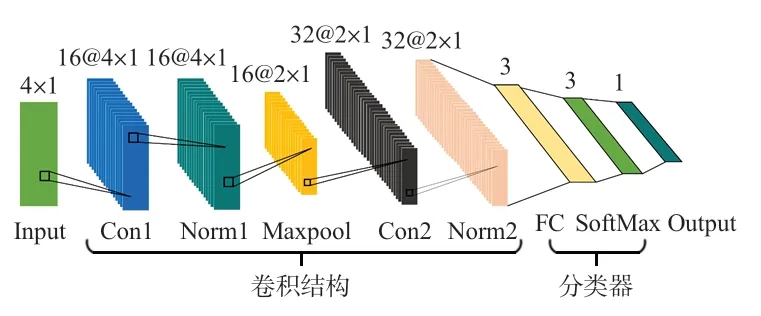
图7 用于下肢步态感知的CNN架构

首先将归一化处理后数据样本作为CNN的输入（Input），经由卷积结构进行数据特征提取，再经过分类器中的FC层将其映射至样本标记空间，然后通过SoftMax 层选择最大预测概率的类别作为分类结果，最终输出至Output。

3.2 试验分析

针对平地行走、平地慢跑和坡路行走3 个步态展开足底压力分布采集试验，利用地面反作用力预测模型分别获取上述3个步态的地面反作用力数据，经过提取特征数据与归一化处理，获得300 组数据样本，并将其划分为CNN所需的训练集与测试集（见表2）。

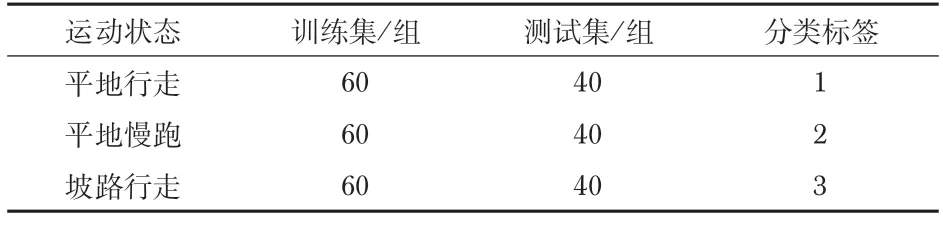
表2 CNN不同步态的训练集与测试集

训练过程中，设置学习率为0.001，训练次数为500，训练集损失值及准确率的结果如图8 所示。可以看出，训练样本的准确率达到98.95%，而损失值在训练400 次后趋于稳定，其值为0.05。

图8 训练集的损失值及准确率

将测试集输入上述训练得到的CNN模型，进行下肢步态感知的测试试验，其结果如图9所示。可以看出，平地行走中40组测试样本的预测结果完全正确，而平地慢跑和坡路行走中各有1组测试样本的预测结果有误。

图9 测试集的测试结果

根据统计测试集各分类标签的真实值和预测值数量，绘制基于测试集的预测分类混淆图（如图10）。可以看出，平地行走、平地慢跑和坡路行走的精确率（Precision）分别为95.2%，100%和100%，召回率（Recall）分别为100%，97.5%和97.5%。

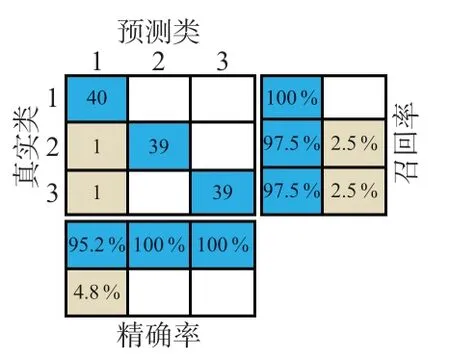
图10 基于测试集的预测分类混淆图

引入Fscore指标（如式（8））综合评价基于测试集的不同步态感知性能

式中 β 为查准率与查全率的调整权重，本文将精确率和召回率视为同等重要，即β ＝1。基于式（8）计算可知平地行走、平地慢跑和坡路行走3 个步态感知的识别率分别为97.5%，98.7%和98.7%，平均识别率达到98.3%，能够满足不同步态感知与运动意图识别的需求。

3.3 对比验证

为进一步验证本文所构建的下肢步态感知CNN 的有效性，分别采用SVM 和BP神经网络替换下肢步态感知流程中的CNN，开展相应的步态感知试验测试，并进行试验结果的对比分析。

基于SVM 的步态感知试验中，选用高斯径向基函数（radial basis function，RBF）为核函数，采用网格搜索和交叉验证的方法，在范围（2－10，210）内寻找最优惩罚参数c和核函数参数g并进行优化，最终获得惩罚参数c为0.015 6，核函数参数g为1。基于BP神经网络的步态感知试验中，隐含层神经元的个数设置为6，输入层到隐含层之间的传递函数设置为tansing，隐含层到输出层之间的传递函数设置为purelin，训练方法为trainlm，最大迭代次数为500，学习率为0.01，训练误差目标为1×10－6。由此可以获得基于不同识别方法的下肢步态感知识别率的对比结果，如表3所示。

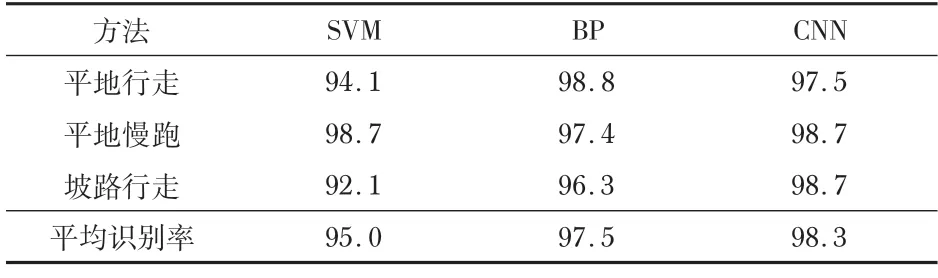
表3 不同识别方法识别率 %

可以看出，本文构建的基于CNN的下肢步态平均识别率达到98.3%，优于SVM和BP神经网络两种方法。为诸如下肢助力外骨骼机器人等相关装置在人机交互技术方面的研究提供了一种可选的方案。

4 结论

本文以足底压力分布为研究对象，基于足底生物力学分析搭建了一种可穿戴式足底压力分布采集装置，并用于平地行走、平地慢跑和坡路行走3 个步态的足底压力数据采集；基于多元线性回归法构建出地面反作用力预测模型，准确地将足底压力分布数据转换为地面反作用力；基于CNN分类算法实现了下肢不同步态的运动感知，并与SVM和BP 神经网络进行对比分析，验证了本文提出的基于CNN分类算法能够更为准确地感知下肢不同步态。这有助于下肢外骨骼能够更好地理解用户意图，可进一步推动下肢外骨骼在康复、行动辅助和劳动增强等应用领域的技术创新。