考虑材料腐蚀的大跨径钢箱梁悬索桥疲劳可靠度分析

丁 亮

(武汉综合交通研究院有限公司 武汉 430010)

伴随着交通建设需求的不断增长,大跨径钢箱梁悬索桥因其造型美观、跨越能力优异,以及传力清晰等优点得到了广泛应用[1]。然而,其在服役过程中难免存在一定的腐蚀和疲劳损伤,将影响桥梁的承载能力和耐久性能[2]。因此,综合考虑大跨径钢箱梁悬索桥腐蚀和疲劳的双重影响,分析其腐蚀疲劳性能退化规律,进而评估钢箱梁服役期时变可靠度性能,将极大保证桥梁的安全运营。

对于钢箱梁腐蚀疲劳的研究,张振浩等[3]引入了腐蚀与疲劳2类因素,结合BP神经网络开展斜拉桥钢箱梁局部构造细节的腐蚀疲劳可靠度评估,并以苏通大桥为例进行了评估。温腾等[4]通过疲劳试验研究表明,节段式钢箱梁腐蚀疲劳的薄弱位置主要为顶板及U肋焊接区域。韩晓东等[5]提出了一种腐蚀疲劳试验方案,该方案可通过特定次数下应变获得钢箱梁在腐蚀环境下的损伤规律。战昂[6]开展了梁桥腹板疲劳试验研究,对材料腐蚀状态下桥梁疲劳裂缝形成和扩展规律进行了系统分析。许睿文等[7]结合有限元方法研究了腐蚀减薄量对钢箱梁服役性能的影响,分析表明桥面板抗拉强度随剩余厚度减薄呈近似线性降低。郑重等[8]通过外推法分析钢箱梁焊接区域热点应力规律,分析发现在使用年限内,由于腐蚀的影响,钢箱梁局部热点应力将超过其对应的屈服强度。董彩常等[9]以红岛航道桥钢箱梁为例,结合实测数据分析了材料腐蚀对钢箱梁抗疲劳性能的影响,分析发现该桥具有良好的抗疲劳寿命。上述研究发现,腐蚀疲劳对钢箱梁的服役性能具有较大影响,但该领域研究大多集中在试验和有限元分析方面,有关其腐蚀疲劳的可靠度研究仍较少,而对于大跨径钢箱梁悬索桥疲劳可靠度分析更鲜有涉及。

鉴于此,本文拟开展考虑材料腐蚀的大跨径钢箱梁悬索桥疲劳可靠度分析,以典型实际工程大跨悬索桥为研究对象,引入考虑腐蚀疲劳的钢箱梁抗力和荷载效应时变模型,结合RBF神经网络方法计算该钢箱梁悬索桥的疲劳可靠指标,并对材料参数进行敏感性分析。

1 考虑腐蚀疲劳的钢箱梁抗力和效应时变模型

1.1 腐蚀疲劳抗力时变模型

大跨径钢箱梁悬索桥腐蚀疲劳的抗力主要表现为材料疲劳破坏的极限强度。参考已有研究,在环境温度和湿度一定的条件下,材料疲劳的极限强度σ可通过抗拉强度fu近似估计,其主要存在如下关系:

σ=38+0.43fu

(1)

考虑钢材强度随时间的影响,由于荷载循环和钢材表面锈蚀影响,大跨径钢箱梁悬索桥内部将逐渐出现裂纹,进而导致钢箱梁强度随之下降,其强度随时间变化的函数R(t)表达为

R(t)=φ(t)R0

(2)

式中:R0和R(t)分别为大跨径钢箱梁悬索桥的初始承载能力和衰减后的结构承载力承载能力随时间的衰减模型;φ(t)为承载能力随时间的衰减模型,φ(t)=1-0.3×10-6t3。

综合式(1)、式(2),得到大跨径钢箱梁悬索桥腐蚀疲劳抗力模型如式(3)。

σ=38+0.43R0(1-0.3×10-6t3)

(3)

1.2 腐蚀疲劳荷载效应时变模型

大跨径钢箱梁悬索桥腐蚀疲劳荷载效应主要表现为车辆往复荷载引起的疲劳效应,假设车辆荷载效应比值服从Gumbel分布,大跨径钢箱梁悬索桥服役时间为t年,结合统计学理论,钢箱梁荷载效应最大值分布函数Ft(x)进一步表示如式(4)。

Ft(x)=exp{-exp[-(x-βt)/αt]}

(4)

式中:βt和αt分别为位置参数和尺度参数。

其中,分布函数Ft(x)的均值μt和标准差σt分别表示为

(5)

再而,基于钢结构腐蚀深度模型,采用指数函数表示为

C=FtB

(6)

假设钢箱梁腐蚀前后厚度分别H0和H,则H可通过腐蚀前的厚度与腐蚀深度的差值表达,即

H=H0-C

(7)

随机变量方面,选取钢材的弹性模量E、横截面面积A、厚度H、汽车荷载P,以及时变效应t作为随机参数,其统计参数和分布类型见表1,计算过程参考文献[3],兹不赘述。进而,大跨径钢箱梁悬索桥构件的腐蚀疲劳荷载效应如式(8)。

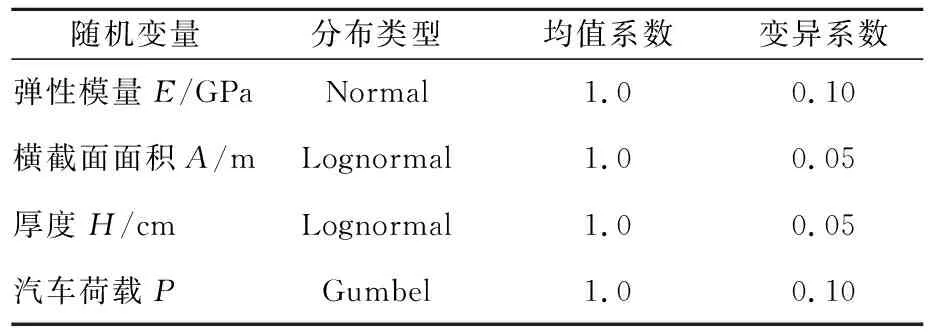
表1 钢箱梁随机变量及其统计参数

Δσ=f(E,A,H,P,t)

(8)

2 基于RBF神经网络的钢箱梁疲劳可靠度计算方法

2.1 RBF神经网络模型

该模型对本文随机变量和疲劳破坏功能函数作为输入和输出进行连接训练,兼具高效性和准确性的优点,具体原理图见图1。

图1 RBF神经网络结构原理图

RBF神经网络模型中,网络输入层和隐含层分别采用随机向量x和向量h表示,具体为

x=[x1,x2,…,xn]T

(9)

h=[h1,h2,…,hn]T

(10)

式中:hi为隐含层中第i个神经元的输出值,通过高斯函数作为基函数,表示为

(11)

隐含层变换到输出层过程中,采用权值向量进行输出,即

Δσ=w1h1+w2h2+…+wnhn=

(12)

2.2 腐蚀疲劳极限状态方程

结合第1节抗力和效应计算方式,大跨径钢箱梁悬索桥的功能函数表示为抗力和效应的差值,即

G(t)=ΔσR(t)-ΔσS(t)

(13)

式中:G(t)为大跨径钢箱梁悬索桥腐蚀疲劳功能函数;ΔσR(t)和ΔσS(t)分别为钢梁腐蚀疲劳承载能力随机过程和荷载效应随机过程。

基于剩余强度疲劳可靠度模型,大跨径钢箱梁悬索桥的极限状态方程可进一步表示为

G(t)=a+b[38+0.43φ(t)R0]-

(14)

2.3 基于RBF神经网络的钢箱梁疲劳可靠度计算流程

基于RBF神经网络的钢箱梁疲劳可靠度计算实际是建立钢箱梁随机变量与荷载效应的关系,得到腐蚀疲劳荷载效应的时变显式表达式,并结合传统可靠度方法计算疲劳可靠指标,具体计算步骤如下。

步骤1。确定大跨径钢箱梁悬索桥悬索桥随机变量的分布类型及统计特征(如表1),并采用LHS抽样选取随机变量样本点。

步骤2。通过有限元方法建立合理准确的大跨径钢箱梁悬索桥非线性力学模型。

步骤3。通过大跨径钢箱梁悬索桥有限元模型,批量计算随机样本点对应的结构响应,进而求解其极限状态函数值(式(13))。

步骤4。将随机变量值和极限状态函数值分别作为输入和输出样本,基于RBF神经网络模型进行网络训练(式(9)～式(12))。

步骤5。通过训练后符合计算精度的神经网络的权值和阈值,确定腐蚀疲劳荷载效应的时变显式表达式,进而得到大跨径钢箱梁悬索桥极限状态方程的显式函数。

步骤6。通过大跨径钢箱梁悬索桥极限状态方程的显式函数,并结合验算点法计算结构的疲劳可靠指标,对钢箱梁悬索桥进行寿命评估。

3 工程实例分析

3.1 有限元模型建立

为说明本文腐蚀疲劳可靠度计算的可行性,以某大跨钢箱梁悬索桥工程为例进行分析。该悬索桥为三跨悬索桥,主跨跨度为1 500 m,标准节段为16 m。采用通用有限元软件ANSYS APDL建立数值模拟,采用LINK10单元模拟主缆和吊索,BEAM4单元模拟分配梁、加劲桁架和桥塔。边界条件方面,对悬索桥两侧施加对称边界条件,桥塔底部施加固定约束。材料强度方面,该桥钢箱梁采用Q355钢材,弹性模量为206 GPa,桥面板和顶板U肋抗拉强度分别为270,275 MPa。最终,有限元模型共1 365个节点和1 268个单元,模型结构和节点模拟处理如下,最终大跨悬索桥数值模型见图2。

图2 大跨钢箱梁悬索桥有限元模型

3.2 疲劳可靠度计算结果

获得腐蚀疲劳状态下大跨径钢箱梁悬索桥桥面板和U肋的极限状态方程后,采用验算点法计算疲劳可靠指标,其使用年限-疲劳可靠度曲线见图3。

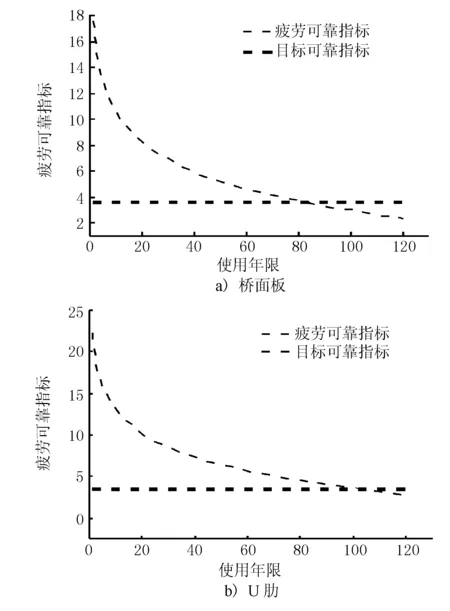
图3 使用年限-疲劳可靠度曲线

由图3可知,桥面板和U肋腐蚀疲劳可靠指标同使用年限成反比,随着使用年限的增大,钢箱梁桥面板和U肋在腐蚀疲劳状态下的可靠指标下降速度逐渐增大,其中桥面板疲劳可靠指标下降最为剧烈。

表2给出了疲劳可靠指标随随使用年限变化数据,根据GB/T 50283-1999 《公路工程结构可靠度统一标准》[10],对于一级延性破坏的桥梁结构,其目标可靠指标不应小于3.7。由表2可见,桥面板和U肋分别在90年和80年以后低于目标可靠指标,说明按规范的目标可靠度要求,该大跨径钢箱梁悬索桥在80年以后将面临失效的风险,与设计年限100年尚存在一定距离,间接说明了开展钢箱梁疲劳可靠度评估的必要性。此外,由表2亦可以看出,随着年限的增长,疲劳可靠指标逐年下降,在10年之内,桥面板和U肋的疲劳可靠指标下降百分比分别高达41.78%和42.26%,120年以后桥面板和U肋的疲劳可靠指标分别为1.526和2.311,下降百分比分别为93.14%和89.61%,远小于目标可靠指标要求,已不适合继续承载。

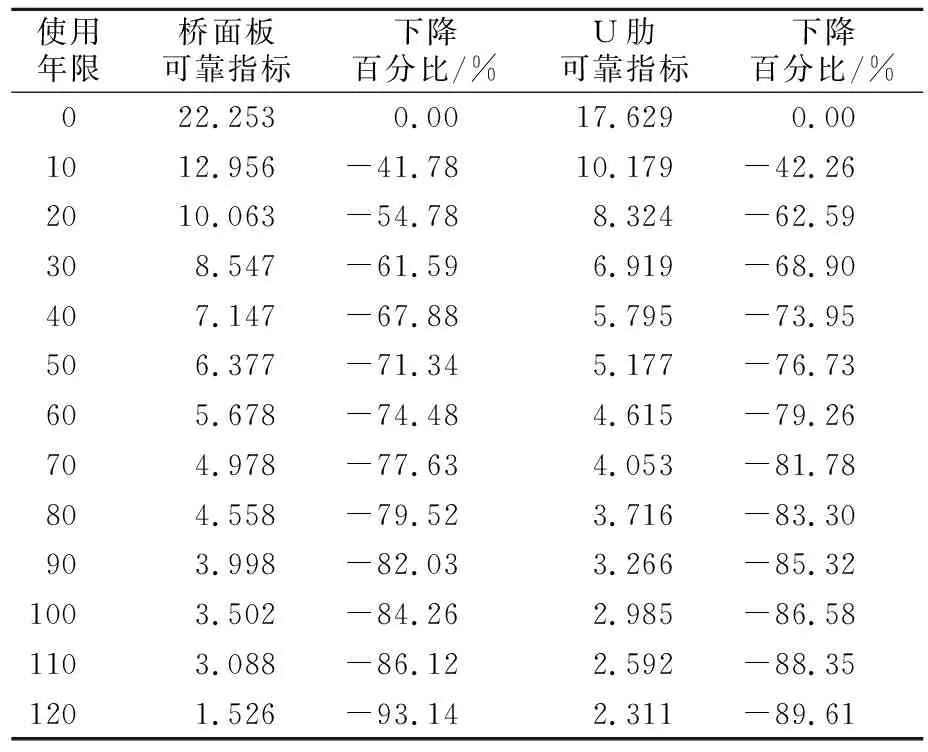
表2 疲劳可靠指标随使用年限变化数据

3.3 材料参数的敏感性分析

以30年腐蚀年限为例,分析钢材的材料参数对大跨径钢箱梁悬索桥疲劳可靠度的敏感程度。钢材强度参数和弹性模量参数对大跨径钢箱梁悬索桥疲劳可靠指标的敏感性曲线分别见图4、图5。如图4、图5所示,随着钢材强度均值和钢材弹性模量均值的增大,钢箱梁桥面板和U肋腐蚀疲劳可靠指标随之增大,而随着钢材强度变异系数(偏差/平均值)和钢材弹性模量变异系数的增大,钢箱梁桥面板和U肋腐蚀疲劳可靠指标随之减小。从总体变化趋势来看,大跨径钢箱梁悬索桥疲劳性能受钢材材料性能较为敏感,因此建议计算疲劳可靠度时有必要重点考虑材料参数的影响。

图4 钢材强度-疲劳可靠度曲线

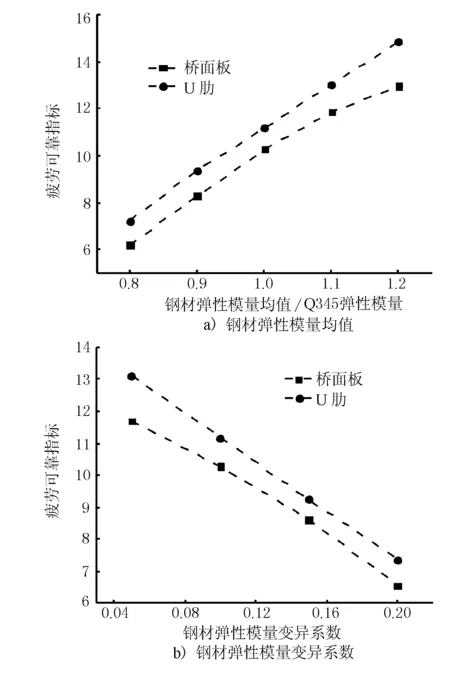
图5 钢材弹性模量-疲劳可靠度曲线

4 结语

腐蚀疲劳是影响大跨径钢箱梁悬索桥服役安全性的重要因素,本文依托典型桥梁工程实例,结合钢箱梁腐蚀疲劳抗力、荷载效应函数,以及RBF神经网络模型开展了考虑材料腐蚀的大跨径钢箱梁悬索桥疲劳可靠度研究工作,得出主要结论如下。

1) 引入腐蚀疲劳抗力和荷载效应时变模型,并基于RBF神经网络模型及非线性有限元方法,建立了考虑材料腐蚀的大跨径钢箱梁悬索桥疲劳可靠度分析方法及计算框架。

2) 根据钢箱梁疲劳可靠度计算结果发现,桥面板和U肋腐蚀疲劳可靠指标同使用年限成反比,并分别在使用90年和80年以后低于目标可靠指标3.7的要求,说明80年以后结构可能面临失效的风险,间接说明了从疲劳可靠性角度预测桥面板的使用寿命的必要性。

3) 由材料参数敏感性分析发现,大跨径钢箱梁悬索桥桥面板和U肋腐蚀疲劳可靠指标同钢材强度均值和弹性模量均值成正比,而与其对应的变异系数成反比,说明大跨径钢箱梁悬索桥疲劳性能对钢材材料性能较为敏感,建议疲劳可靠度评估时应重点考虑材料参数的影响。