基于改进粒子群算法的地铁隧道维护策略优化*

顾亦宁 艾 青 袁 勇

(1.上海交通大学船舶海洋与建筑工程学院, 200240, 上海; 2.同济大学地下建筑与工程系, 200092, 上海)

地铁隧道由于自身建设历史、地理位置和结构型式各异,其维护工作具体细节可能不同,但总体上可归纳为检查、服役性能评估和维修等几项主要任务。以上海轨道交通为例,隧道维护采用定期检查模式,以服役性能评估结论为依据,从结构安全角度判断是否需要进行预防性维修。上海轨道交通隧道维护工作实践取得了良好效果,近年来未发生过较大的结构安全问题。然而,由于我国大部分城市的地铁运行时间尚短、服役状态尚好,定期检查模式和经验性预防性维修存在的问题还未暴露。由发达国家的经验可知,基础设施在服役后期将发生大规模退化,维护资源短缺问题难以避免,管理部门将面临严峻的工作量和资金预算压力。因此,为了提升地铁隧道维护的科学性,有必要进行维护策略优化,在保障地铁隧道高水平服役运行的前提下降低全寿命期维护成本。

本文采用隧道结构状态导向维护方法[1]中的非周期性检查模式和控制-极限维修规则,探究通过对检查维修方案中的变量取值进行组合,达到对地铁隧道维护过程和全寿命期维护成本进行优化管控的目的。

1 地铁隧道维护策略优化模型

1.1 地铁隧道服役性能退化过程

地铁隧道服役性能退化过程可用Gamma过程表示[1-2]。Gamma过程是单调递增的随机过程模型,非常适合描述以累积损伤为特征的地铁隧道退化过程,其概率密度函数gX(t)(x)为:

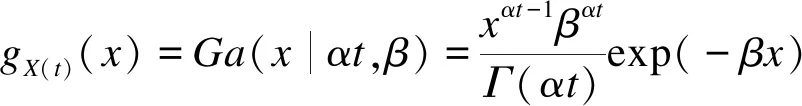
(1)

式中:

X(t)——t时刻的地铁隧道服役性能退化指标;

α——Gamma过程的形状参数;

β——Gamma过程的尺度参数;

Ga(x|αt,β)——形状参数为αt,尺度参数为β的Gamma分布;

Γ(x)——Gamma函数。

地铁隧道服役性能退化并不严格遵循上述稳态增长的Gamma过程,由于不同的退化机制,可能会出现加速或减速的现象[3]。因此,使用时间转换方法建立非稳态Gamma过程,即在稳态Gamma过程中使时刻t与t+Δt之间的增量Δt满足式(2)—式(4):

X(0)=0

(2)

X(t+Δt)-X(t)～Ga(v(t+Δt)-v(t),β),

Δt>0

(3)

v(t)=ctq

(4)

式中:

v(t)——时间转换方程;

c——时间转换方程中的拟合常数;

q——时间转换方程中的拟合幂指数。

1.2 检查计划函数

一般认为,随着地铁隧道服役性能退化程度上升,需要减小检查时间间隔。因此,结合以往非周期性检查研究结论[3-4],采用的检查计划函数为递减凸函数,即:

Tinsp(X(t))=

(5)

式中:

Tinsp(X(t))——检查时间间隔;

a——初始检查时间间隔;

b——地铁隧道服役性能退化临界指标,表示地铁隧道已接近失效,超过该指标后需每年进行一次检查。

1.3 维修措施效果

令A(t)表示地铁隧道维修措施效果,X′(t)表示执行维修措施后地铁隧道的服役性能退化指标。由于地铁隧道维修措施大多数为隐蔽措施,其效果不确定性较强,因此,假设A(t)为随着隧道退化指标上升而下降的随机数,则:

(6)

式中:

s——预防性维修阈值,当X(t)大于该数值时进行预防性维修;

f——失效阈值,当X(t)大于该数值时进行重建;

R——预防性维修效果的基础值,服从下限值l至上限值u之间的均匀分布,即R～U(l,u)。

1.4 全寿命期维护成本

地铁隧道全寿命期维护成本等于所有检查、预防性维修和重建的总成本。由于隧道的退化过程和维护措施效果都存在随机性,因此可通过N次蒙特卡洛模拟求全寿命期维护成本的期望值E(Clife),其计算公式如下:

E(Clife)=CinspE(Qinsp)+CprE(Qpr)+

CfE(Qf)

(7)

式中:

Cinsp、Cpr、Cf——地铁隧道单次检查成本、单次预防性维修成本和重建成本;

Qinsp、Qpr、Qf——检查次数、维修次数和重建次数;

E(·)——数学期望操作符。

1.5 参数取值和决策变量

1) 退化过程。以地铁隧道中常见的管片锈蚀引起隧道收敛变形增大为典型退化机制,可认为地铁隧道服役性能退化过程服从加速退化模式[3]。Gamma过程的参数取值为:c=0.006,q=2,β=0.5。

2) 检查计划函数。为方便执行检查计划,Tinsp(X(t))、a应为整数。在初始状态,隧道服役性能未产生退化,此时Tinsp(0)=a,即最长检查时间间隔为a。在工程实践中,地铁隧道检查时间间隔不宜过长,假设a的取值范围为[1年,20年]。当X(t)接近b时,Tinsp(X(t))≈1年,需要每年对地铁隧道进行检查以降低失效风险。一般认为b≤f。根据相关试验结果,地铁隧道收敛变形在大于140 mm(即X(t)>140 mm)后会快速增长,因此可以取f=140 mm[5]。为提供一定安全储备,b略小于f,可以取b=130 mm。

3) 维修措施效果。假设维修措施效果的基础值服从-30至-20的均匀分布,即R～U(-30,-20)。s的工程单位为mm,取整数值。

4) 维护成本。假设不同维护措施的成本取值为:Cinsp=0.01万元,Cpr=500万元,Cf=500 000万元。需要说明的是,维护措施成本因受不同地区经济水平和技术发展变化影响会存在一定差异,本案例主要关注各类成本之间的比值关系。

5) 决策变量。本优化问题的决策变量包括a和s。

为了反映地铁隧道真实退化过程和维修措施效果,本模型引入了大量不确定性,因此其优化问题难以通过规划模型或网络模型等方法求解,为避免参数组合叠加蒙特卡洛模拟带来的大量计算需求,需要提出高效的优化求解算法。

2 维护策略优化的改进粒子群算法

2.1 模型的随机性分析

首先,在s和a取值不同的情况下进行几次试验,大致探索参数s和a对目标函数E(Clife)的影响及模型的收敛规律。结果表明,当s取值较小(s<100 mm)时,大量的预防性维修会导致E(Clife)很高。此时,当模拟次数N较大(N≥1×106次)时,计算结果稳定,但是计算非常耗时;而减小N(N≈2×104次),计算时长可以接受,但是计算结果不稳定。当s取值较大(约s>125 mm)时,在E(Clife)中预防性维修占比较低,重建成本占比很高。因此,当蒙特卡洛模拟次数N较小时,可能会造成E(Clife)出现异常高值或异常低值的现象,这种偶然出现的异常低值称为伪最优解。

粒子群算法是一种较高效的启发式优化算法,可用于求解带有随机性的优化问题[6]。在传统粒子群算法中,若N设为较大的值,所得结果相对可靠,但计算效率很低;若N设为较小的值,一旦伪最优解在某次迭代中出现,则全局最优解容易陷于这个异常解中,从而给出错误的解。为保证计算效率和结果可靠性,本文提出了一种改进粒子群算法来求解上述优化问题。

2.2 改进粒子群算法

基于传统粒子群算法,首先采用较小的模拟次数Ns=2×104次在每次迭代中粗略但快速地求解。若在此过程中出现了新的个体最优解,则在较大的模拟次数Nm=2×105次下对该个体最优解再进行3次计算,以判断该个体最优解是否为伪最优解。本研究提出的改进粒子群算法的伪代码如图1所示。

图1 改进粒子群算法截图

若Ns下求得的解与Nm下求得的解相比误差小于15%,则认为该个体最优解是真实解。若此个体最优解小于当前的全局最优解,则更新全局最优解为3次Nm下求得的解的均值。

若Ns下求得的解与Nm下求得的解相比误差大于15%,则认为该个体最优解是伪最优解,将其更正为3次Nm下求得的解的均值。

在伪最优解出现的情形中,为保证全局最优解仍能得到更新,算法将寻找次小个体最优解并将其与全局最优解进行比较。在Nm下对次小个体最优解进行3次计算并取均值。若该个体最优解小于全局最优解,则更新全局最优解为该个体最优解。

改进粒子群算法的参数设置为:粒子数为20个,最大迭代次数为50次,个体和全局学习率均为2,惯性权重随着迭代次数线性下降,最大和最小惯性权重分别为0.8和0.4,以保证算法在早期拥有较强的全局搜索能力,而在后期拥有较强的局部搜索能力使算法收敛。

2.3 求解过程分析

根据2.1节的分析结果,将s的搜索范围划定为[100 mm,125 mm],a的搜索范围划定为[1年,20年]。采用改进粒子群算法在50次迭代后得到最优成本期望值E(Clife)=215.24万元,对应的s=122 mm,a=11年。E(Clife)随着迭代次数的下降过程如图2所示。由图2可见E(Clife)最终收敛至稳定值,即所提出的改进粒子群算法适用于求解本优化问题。

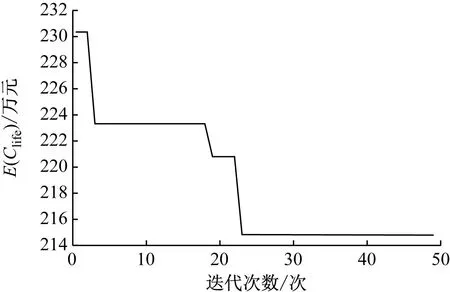
图2 目标函数迭代收敛过程

3 算法验证与分析

3.1 改进粒子群算法验证

为验证改进粒子群算法的准确性,将其计算的最优解与网格枚举法计算结果进行对比。构建参数组合,s分别取值为101、104、107、110、113、116、 119、122和125 mm,a分别取值为1、 5、 9、 13、 17和20年,在N=1×106的条件下共进行54次蒙特卡洛试验。E(Clife)较小的3个值分别为226.97、 227.40和231.04万元,对应的s均为122 mm,a分别为9、20、5年,与2.3节中的改进粒子群算法结果十分接近。

根据网格枚举法计算结果,绘制s和a组合下E(Clife)的等值线图,如图3所示。由图3可见,E(Clife)对a不敏感,对s更敏感。另外,改进粒子群算法解(图中圆点)恰好落在等值线图的中心。

图3 不同s和a取值下的E(Clife)等值线图

进一步研究不同s和a对E(Clife)的影响,在最优解附近进行多次(N=1×106次)的蒙特卡洛试验,进一步分析参数敏感性和最优解准确值。

图4为当a固定取最优值(a=11年)时不同预防性维修阈值s下的E(Clife),以及由改进粒子群算法得到的最优解。

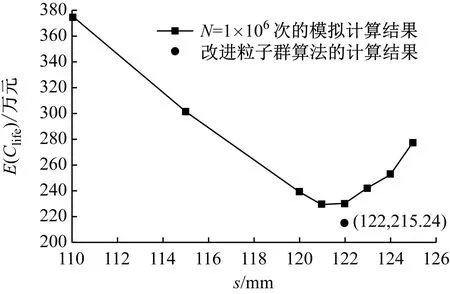
图4 a取最优值时不同s下的E(Clife)

当s小于121 mm时,E(Clife)随着s的增大而减小;当s大于122 mm时,E(Clife)随着s的增大而增大。产生该现象的原因是,当s过大时,地铁隧道的失效概率增加,而Cf很高,这将会极大地增加E(Clife)。

在N=1×106次的试验结果中,E(Clife)次小值出现在s=122 mm和a=11年组合,与改进粒子群算法的结果一致。E(Clife)次小值为230.59万元,与E(Clife)最小值仅相差0.32%,与改进粒子群算法结果相差6.67%。

图5为当s固定取最优值(s=122 mm)时不同a下的E(Clife),以及由改进粒子群算法得到的最优解。

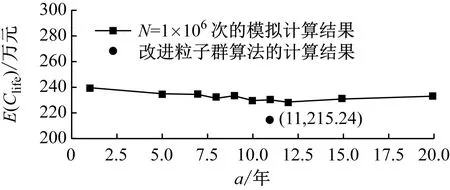
图5 s取最优值时不同a下的E(Clife)

图5结果与图3结果基本一致,E(Clife)对a的变化较不敏感。在N=1×106次的试验结果中,E(Clife)较小的3个值分别为228.68、229.75和230.89万元,分别对应a为12、10和11年。三者之间非常相近,相互之间仅相差0.47%和0.96%。改进粒子群算法结果与第三小的解都位于a=11年处,二者E(Clife)之间相差6.78%。

结合图3—图5计算结果进行比较分析:由于本优化问题假设大多数参数取值均为整数,因此该优化问题可能存在多解的情况;考虑到改进粒子群算法的最优E(Clife)更低以及等值线图指示的最优解所在区域,可认为改进粒子群算法可以较高效、准确地求解本优化问题。

3.2 改进粒子群算法的评价与讨论

1) 计算成本。本文所提出的改进粒子群算法在每次迭代中需要对20个粒子分别进行2×104次计算,并且对2个粒子分别进行至多3×2×105次计算,在50次迭代中,总共最多进行8×107次计算。网格化枚举可以保证得到最优解,但是需要巨大的计算成本。虽然已将决策变量约定为整数,已极大地降低了计算代价,但s和a分别有26和20种取值,共有520种组合,对于每种组合需要进行1×106次计算以保证结果收敛,总共需要进行5.2×108次计算,是改进粒子群算法的6.5倍。可见,在计算成本上,改进粒子群算法具有明显优势。

2) 求解精度。对于所提出的随机优化问题,改进粒子群算法虽然难以保证给出严格的最优解,但是可以给出与最优解非常接近的满意解,对于本问题,其求解精度已满足工程需求。此外,适当增加改进粒子群算法的蒙特卡洛模拟次数,预期可以得到更为准确的最优解。

3) 适用情景。改进粒子群算法更适用于决策变量多、组合复杂的优化问题。对于一些不太复杂的优化情景,可以设计层次化、精细程度不同的网格枚举方法,从而降低枚举法的总成本,在这种情形下枚举法可能更为高效、可靠。

4 结语

本文提出了一种对地铁隧道维护策略进行优化的改进粒子群算法,分析了不同决策变量对全寿命期维护成本的影响,并对改进粒子群算法的应用效果进行了评估。主要结论如下:

1) 本文所提出的改进粒子群算法极大地提升了随机优化问题的计算效率,可以得到与最优解非常接近的满意解。对于本问题其求解精度满足工程需求。相比于网格枚举法,所提出的改进粒子群算法更适用于决策变量多、组合复杂的优化问题。

2) 通过维护策略优化可以降低地铁隧道全寿命期维护成本。在决策变量中,预防性维修阈值比初始检查时间间隔更为敏感。因此,建议在工程实践中合理设定预防性维修阈值,在保证安全的前提下尽可能减少维修次数,降低地铁隧道的全寿命期维护成本。