基于损失变化的CNN混合精度量化方法

何益智，李 钊+，李鉴柏，张少爽，刘文龙

(1.山东理工大学 计算机科学与技术学院，山东 淄博 255000；2.淄博职业学院 电子电气工程学院，山东 淄博 255000)

0 引 言

边缘计算由于其低延迟、低成本、低功耗、隐私保护等优点在近年被广泛研究。然而，许多CNN模型因为其较高的计算成本和内存占用，减缓了模型推理和训练速度[1]，限制了它们在边缘设备上的应用。因此，研究人员提出了许多CNN模型的压缩方法。

Howard等[2]提出了一种轻量级CNN模型Mobilenet-V3采用深度可分离卷积代替传统的卷积计算，极大地降低了参数数量。He等[3]提出一种基于卷积核范数的卷积核剪枝方法，删除可以被替代的网络层，降低模型中的冗余度。另外，还提出了许多量化方法，在文献[4]中表明，CNN模型中参数可以被量化为低位宽定点数，代替32位浮点数运算，节约硬件资源，提高运算速度，便于部署在FPGA(field programmable gate array)等移动平台。Liu等[5，6]提出超低位宽量化方法，将权重和激活值量化到1或-1。然而在超低位宽的情况下使用统一的量化位宽会严重影响模型的性能，解决这个问题的一个非常有效的方法是通过混合精度量化。已有工作使用的强化学习[7]或者可微分搜索混合精度量化[8]允许神经网络的每一层拥有不同的量化位宽，在很大程度上保证模型的推理准确率，但是确定每一层的位宽导致了一个指数级的搜索空间，同时每搜索一步都需要重训练CNN模型，使得已有算法非常耗时。

针对上述问题，本文提出一种基于损失变化的混合精度量化方法，根据量化层的一阶和二阶导数信息确定量化层的敏感度，指导位宽分配。然后利用K-means方法将敏感度相近的量化层聚类为量化块，以块为单位调整位宽分配策略降低搜索空间。同时提出一种自适应量化策略搜索方式，根据按历史策略训练后的反馈结果自行调整“压缩态”和“恢复态”，可在压缩模型的同时确保模型推理准确率始终控制在设定范围内。此外，将量化训练中的参数量化和BN(batch normalization)层进行整合，以减少传统量化训练中冗余的乘法计算，在不影响结果的条件下可加速量化训练过程。

1 基于损失变化的混合精度策略搜索设计

CNN模型中存在大量乘加运算，采用全精度浮点数进行运算需要较高的算力，并且乘加运算主要集中在卷积层和全连接层，因此选取出以上网络层作为量化层，将量化层按照混合精度策略分配不同量化位宽。该过程具体思路如图1所示。

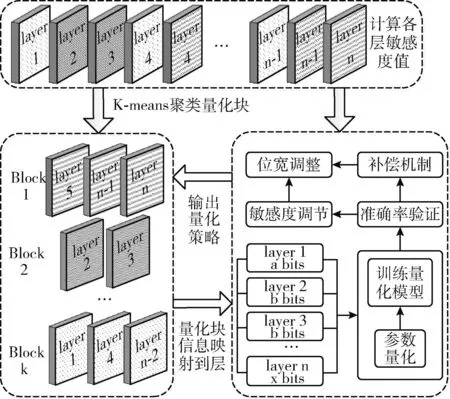
图1 混合精度量化方法框架

首先计算出CNN模型中各量化层加入干扰后引起的模型损失变化量，依据损失变化量确定每个量化层敏感度值，然后采用K-means方法根据量化层敏感度值将其聚类成量化块。把策略搜索模块得出的量化策略对应到每个量化块中，进而传递到所有量化层中。按照策略重新训练网络，并将训练结果反馈给策略搜索模块，根据反馈结果和敏感度调整输出策略，直至找到最佳位宽分配策略。

1.1 量化后模型损失值变化分析

模型量化后产生的损失值变化是由于CNN模型中原32位浮点型参数通过量化转化成n位表示的低位宽数后，两种数据类型间的误差导致的，我们对参数量化过程和损失值的变化做出理论分析。首先由32位浮点数X转化为n位整数Xint，过程如式(1)所示

(1)

其中，Qmin=-2n-1，Qmax=2n-1-1，z为常数，表示零点，S为缩放因子，其计算表达式如式(2)所示

(2)

Xmax和Xmin分别为X集合中最大值和最小值，round()为取整函数，clamp()函数定义式(3)为

(3)

随后按照式(4)恢复成近似原值X的可用n位表示的数XQ

XQ=(Xint+z)×S

(4)

因此X值经过式(1)，式(4)量化成XQ后产生一个了量化误差。同理CNN模型中权重值W量化后变为WQ，WQ代替原32位浮点数W引起了模型损失函数值的变化，该过程如图2所示。

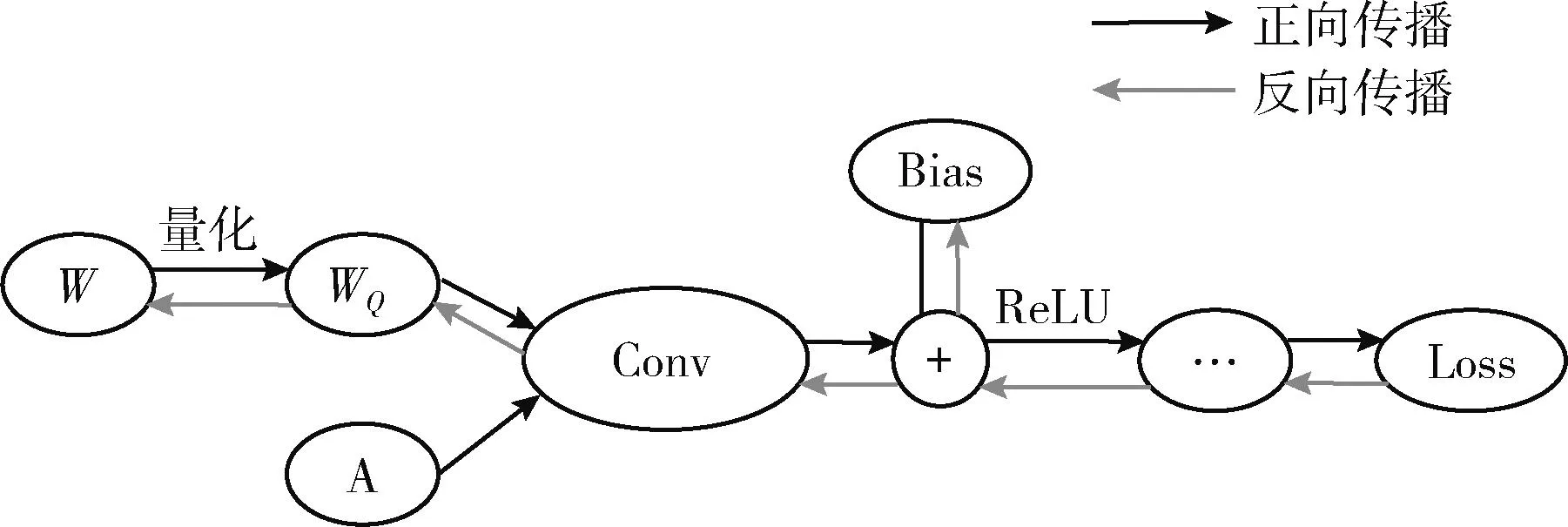
图2 经过量化后的部分CNN模型

把量化误差视为一种干扰，并且在原参数W处利用泰勒公式展开，可近似计算出由量化引起的模型损失变化[9]如式(5)所示

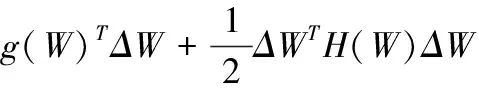
(5)

ΔW为量化引起的误差，L表示损失函数，g为关于参数W的一阶导数，H为关于参数W的二阶导数(Hessian矩阵)。一般情况下，模型量化后会造成损失函数值的增大和推理准确率的下降。因此，为保证模型量化后的推理准确率，需将目标函数ΔL取最小值，ΔL表示为

(6)

从上式可以看出量化后引起的损失值变化与每层网络的一阶，二阶导数信息和量化误差ΔW相关。

1.2 计算量化层敏感度值

通过以上分析可以表明量化后模型损失值在一阶和二阶信息下都会受到影响。在研究二阶信息带来的损失变化时，由于在CNN模型中的权重数据很多，直接计算Hessian矩阵相关值十分困难。所以，可利用幂迭代方法来近似估计Hessian矩阵的最大特征值，沿对应的特征向量方向对每层网络参数加入干扰，衡量模型损失变化量[10]。

因此我们可以对模型中每个量化层中分别加入梯度方向和Hessian矩阵特征向量方向上的扰动，作为量化误差。然后分别计算模型损失函数值，用损失函数变化值衡量每个量化层的一阶和二阶信息带来的影响，作为量化层的敏感度值，根据敏感度值合理分配位宽。具体过程如算法1所示：

算法1：量化层敏感度计算

输入：预训练模型，训练数据集

输出：各量化层敏感度值

(1) 计算预训练模型的损失值Loss=Criterion(Model(inputs),targets)

(2) 计算各量化层权重的一阶导数g=Loss.backward()

(3) fori=1 toNdo:

(4) 设置一个与第i个量化层相同维度的随机向量Vi=random(gi)

(5) 标准化Vi=normalization(Vi)

(6) forj=1 toMaxIterdo:

(7) 计算第i个量化层Hessian矩阵特性向量,记作HiVi

(8) 标准化Vi=normalization(HiVi)

(9) end for

(10) 第i个量化层加入第一种干扰Wi=Wi+λ·direction(gi)

(11) 计算加入干扰后的模型损失值L1=Loss(Model(inputs,W),targets)

(12) 第i个量化层加入第二种干扰Wi=Wi+λ·direction(Vi)

(13) 重新计算模型损失值L2

(14) 确定每个量化层敏感度值Si=Max(L1,L2)

(15) end for

在算法1中，步骤(1)～步骤(9)介绍了幂迭代法的过程，首先按照步骤(1)利用常见的交叉熵损失函数Criterion()计算预训练模型的损失值，通过步骤(2)反向传播计算出预训练模型中各个量化层的梯度g。接下来选取第i个量化层，初始化一个随机向量v，要求与目前第i个量化层维度相同，并做归一化处理，如步骤(4)、步骤(5)所示。通过步骤(7)对该层的Hessian矩阵的特征向量HiVi，采用如式(7)所示链式求导法则，其中gi，Hi，Wi分别为第i层的一阶导数、二阶导数和权重

(7)

按照步骤(8)把该值归一化处理后迭代执行步骤(7)、步骤(8)，则计算出预训练模型第i个量化层梯度和Hessian矩阵的最大特征值对应的特征向量。然后在这两个方向上加入干扰值作为量化产生误差。步骤(10)、步骤(11)表示对第i个量化层施加梯度方向的干扰，并计算在该层受到扰动后整个CNN模型损失值L1，λ值可用来调整扰动值大小。步骤(12)、步骤(13)表示对第i个量化层施加最大特征向量方向的干扰，然后重新计算其模型损失值L2。最后取L1和L2的最大值作为第i个量化层敏感度值。按照上述流程计算出所有量化层敏感度值。

在文献中[11]，仅采用一阶信息作为敏感度值，可能会造成位宽分配不合理的情况。例如在一个函数的极小值点处，此时一阶导数为零，假设极小值处二阶导数大，曲线曲率大，即使加入较小的干扰也会引起函数值较大的变化。若只把一阶信息作为衡量敏感度的指标，则在后续过程中可能导致位宽分配不合理。因此需要综合考虑根据每个量化层的一阶和二阶信息，可更加准确判断每个量化层对整个CNN模型的影响大小，选择出更合适的位宽值。

1.3 K-means聚类量化层

目前量化研究已经可以实现在统一分配8位及以上位宽情况下，实现无损压缩。本文提出的方法是在此基础上探索更高压缩比，所以量化位宽设定为2～8位。但是为模型中所有量化层确定位宽会带来指数级搜索空间，因此提出采用K-means方法根据量化层的敏感度值将其聚类成量化块，以量化块为最小单位调整位宽分配策略，降低搜索空间。其中关键问题是对K值的选择，在本文中K值选择是基于量化策略的设定，网络中所有量化层位宽均在[2，8]区间内，在理想情况下，根据位宽数可将所有量化层分为7个量化块，因此可将K值设定为7。

假设CNN模型中有n个量化层，需把所有量化层集合N={N1，N2，…，Nn} 聚类到k个量化块集合K={K1，K2，…，Kk} 中。从所有量化层中随机选择k个量化层的敏感度值作为k个量化块的质心，并根据距离式(8)计算出每个量化层Ni与量化块质心μj的距离，并把所有量化层就近归入到量化块中

(8)

其中，S(Ni) 表示量化层Ni的敏感度值，μj为第j个量化块的质心，量化层加入到量化块后，根据质心计算式(9)更新每个量化块的质心值

(9)

迭代计算式(8)、式(9)，使得目标函数(10)达到收敛状态。即每个量化块中的量化层处于稳定状态，不再做出调整，质心不再发生变化，各量化层敏感度与质心误差平方和达到最小，则完成将量化层聚类为量化块的过程

(10)

1.4 自适应搜索设计

由于原敏感度值表示较为复杂，在搜索设计时不便于使用，因此采用相对敏感度代替原敏感度。把所有量化块K的质心μ从大到小排序，把排序后的相对顺序值设定为量化块的相对敏感度值S′，可表示为

S′i=Sort(μi)

(11)

考虑到敏感度大的量化块在量化时会引起更明显的扰动，则设计搜索方法时，需要按照S′值依次确定量化块的位宽值，同时满足高敏感度值的量化块分配的位宽要不少于低敏感度量化块的原则。具体设计流程如图3所示。

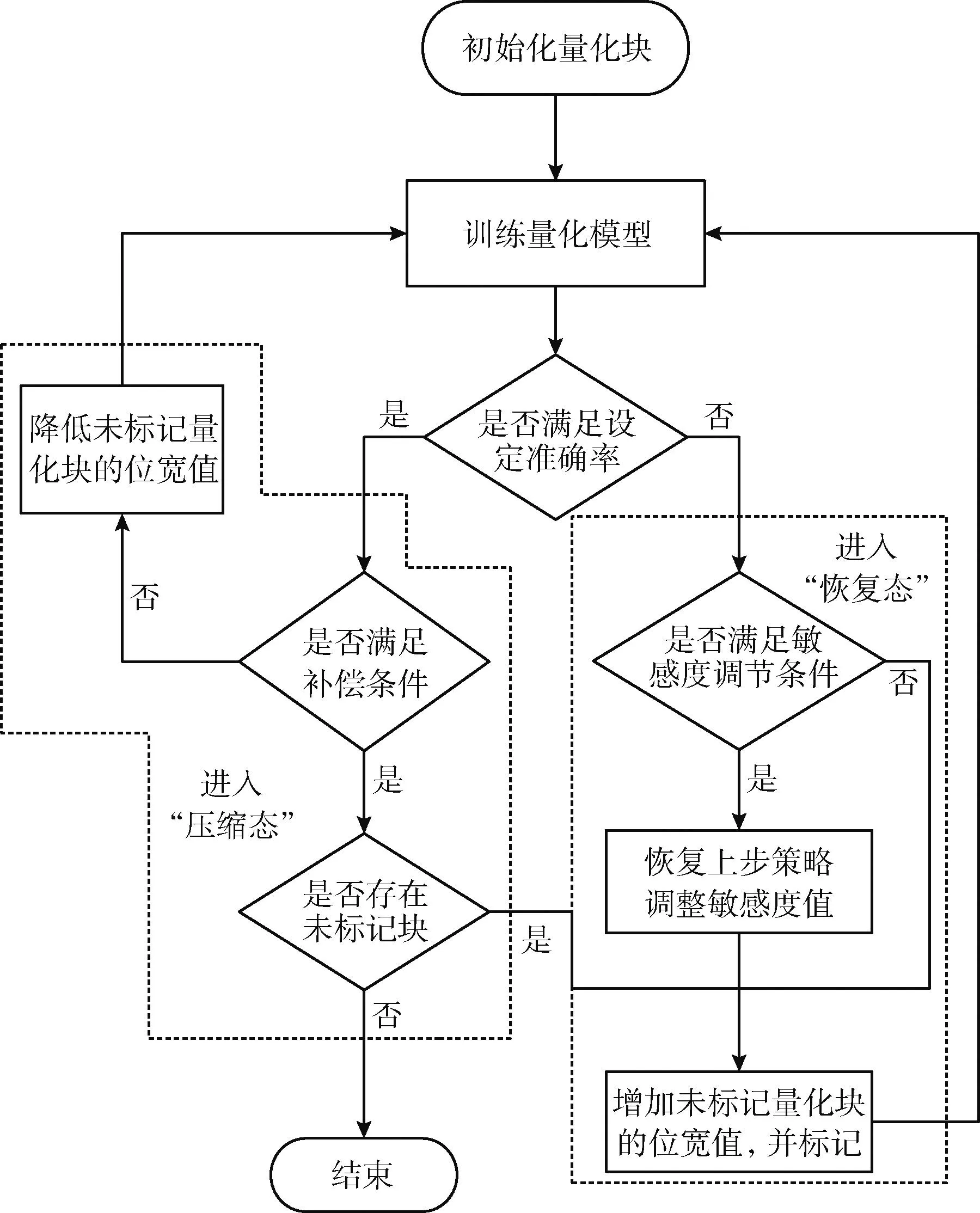
图3 策略搜索流程

首先，将所有量化块设定为未标记状态，所有位宽设定为8位，从全8位量化开始搜索。并设定了两种搜索状态：“压缩态”，在该状态下降低所有未标记量化块位宽数；“恢复态”，即逐步增加未标记量化块中量化块的位宽数。

每确定一个位宽分配策略，均按照此策略采用第2节所述量化方法训练模型，将训练结果与设定的准确率比较结果，若满足设定要求，则将当前搜索策略置于“压缩态”，将所有未标记量化块位宽数减1；若不满足设定要求，则将当前搜索策略置于“恢复态”，选择未标记且具有最大S′值的量化块，增加其位宽数。按照更新后的量化策略重新训练模型，判断结果是否满足设定要求，若不能满足设定要求，仍然按照“恢复态”增加量化块位宽数；若能满足，则把选择的量化块都置为已标记状态，位宽设定为当前策略下的位宽值，直至所有量化块都置为已标记状态。策略搜索方法均以量化块为单位，相比于以层为单位调整位宽可避免大量无效的量化策略，加快搜索过程。

在实验过程中发现，在策略搜索处于“压缩态”时，虽然位宽减小后可以达到设定的精度要求，但是当前策略与历史策略模型推理准确率变化较大，则在后续压缩过程中并不利于找到最优解，易陷入局部最优。为避免该情况的出现，在“压缩态”种嵌入补偿机制，即在策略搜索处于“压缩态”时，若满足式(12)，将当前搜索策略切换到“恢复态”，按照相对敏感度值依次恢复量化块的位宽值，直至不满足式(12)，继续进行压缩

Plast-Pnew≥α(P-Pset)

(12)

其中，Plast为历史策略下模型准确率，Pnew为当前策略下模型准确率，P为全精度模型准确率，Pset为目标准确率，α为超参数，可根据Pset调节。

另外，在“恢复态”中引入敏感度调节模块。某些量化块在增加位宽，训练结果较之前没有明显改善，故引入该模块可根据实际训练结果动态调节量化块。即在搜索策略处于“恢复态”时，若Pnew-Plast≤0，将策略恢复成历史策略，并且降低对应量化块的相对敏感度值。

2 量化训练

一般情况下，原32位浮点型权重量化成低位宽数后，模型推理准确率会有较大损失，因此采用量化训练恢复原有的准确率。本文提出将量化训练中的参数量化和BN层合并，改变传统量化训练中原有的卷积操作，在不影响结果的条件下可减少计算量。同时考虑到量化后CNN模型能充分发挥边缘计算平台的优势，将同一量化层中的权重和输入特征量化为相同的位宽数，可在后续工作中采用定制乘法器提高资源利用率，降低模型部署难度。

在CNN模型中，为加快模型收敛速度，防止梯度爆炸，梯度消失和过拟合等问题，许多网络设有BN层。但是这个网络层带来的额外计算量使得神经网络在硬件资源有限的平台更加难以实现，因此可以通过将BN层与卷积层融合，可减缓硬件资源压力。

假设在某个卷积层中权重为W，输入特征为A，则卷积过程可以表示为

Yconv=W*A+b

(13)

BN层计算过程可以表示为

(14)

μ，σ分别表示为一个batch内的均值和标准差，γ表示缩放参数，β为偏移参数，ε为一个非常小的常数，设定为0.001，则卷积层与BN层融合后整个过程可表示为

Y=W′*A+b′

(15)

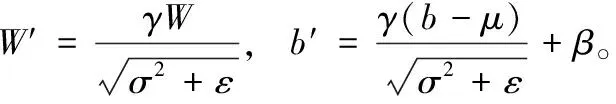
在传统量化训练中常用计算方法是通过式(4)和式(15)按顺序计算结果。为进一步加快量化训练过程，我们将参数量化，卷积层与BN层重新整合。将式(4)和式(15)结合，可得式(16)

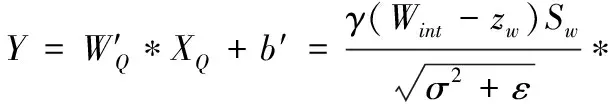
[(Xint-zw)Sx]+b′

(16)

由于卷积运算为线性运算，因此可以将把式(16)可转化为

Y=(Wint-zw)*(Xint-zx)Sy+b′

(17)

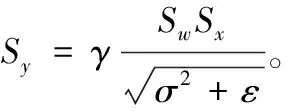
在量化训练中，常用层级量化与通道级量化两种量化粒度，可根据实际情况选择。若量化粒度选为层级量化，则Sw和Sx在每个量化层中为一组定值，因此在改进传统的量化训练后每个量化层中Sy只需计算一次，最后与卷积运算后的结果相乘即可；若量化粒度选为通道级量化，则Sw和Sx在每个通道内为一组定值，在每个通道内计算一次Sy值即可。另外，若量化方式采用对称量化，即zw=zx=0，式(17)中卷积运算可转化为整型运算，结合目前许多GPU中的Tensor Cores技术(可支持INT8和INT4等不同的精度模式)，可进一步提高模型训练速度。

3 实验验证

为了验证本文提出方法的有效性，选取常用对比网络Resnet18、Resnet20、Resnet56在cifar-10和cifar-100数据集上进行量化实验，分别测试3种CNN模型量化后的分类准确率和位宽。

实验环境采用深度学习框架pytorch，在配有NVIDIA Tesla T4 GPU的LINUX系统服务器中完成模型预训练和量化实验过程。在训练全精度模型时初始学习率设定为0.01，每训练100轮调整到原来的1/10，量化训练时学习率统一定为10-4，均使用SGD优化器调整模型权重。

设定模型量化后推理准确率损失小于1%(可根据实际需求调整该设定值)。在量化实验前，将全精度模型训练300轮后选取具有最高准确率的模型作为量化实验的预训练模型。每种量化策略训练20轮，保存每种量化策略与对应的最高记录作为实验结果。实验从压缩比和量化后的CNN模型推理准确率两方面进行对比分析，通过准确率的变化和压缩比衡量量化工作的可行性。

3.1 cifar-10数据集上的量化实验

实验选取cifar-10数据集，该数据集包含5万张训练图片和1万张测试图片，共10类物体图像。在上述设定条件下进行量化实验，测试原模型和量化后的模型分类准确率以及位宽值。具体实验结果见表1。

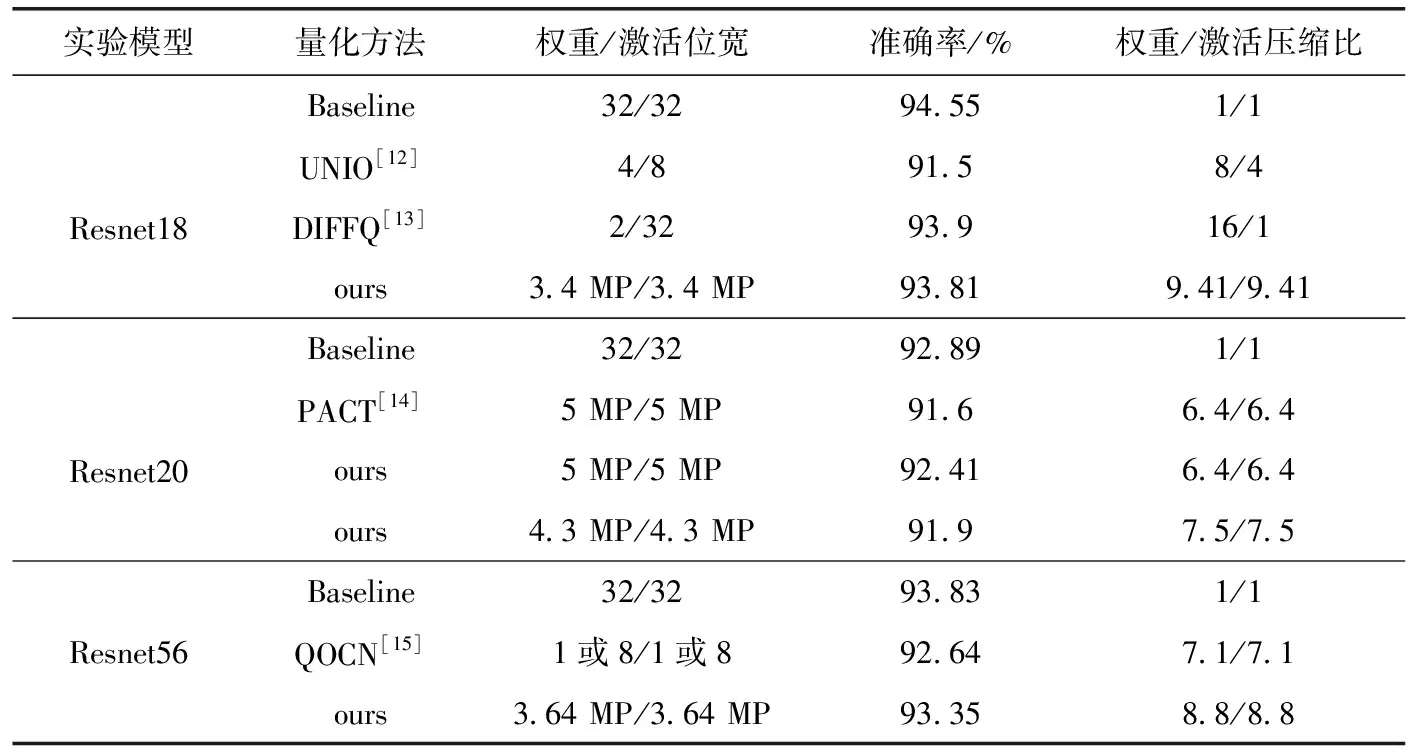
表1 cifar-10数据集中量化实验结果

Resnet18网络预训练后，推理准确率为94.55%，将预训练量化后其推理准确率仍然可达到93.81%，权重和激活值位宽可从32位量化至3.4 MP(MP表示为混合精度量化的平均位宽值)，在准确率仅损失0.74%的情况下，权重位宽与激活位宽平均压缩9.41倍，其内存占用空间仅为全精度模型的10.63%。表1中另外给出了Resnet18网络使用不同量化方法得到权重和激活的位宽，压缩比以及模型的准确率。可以看出，与UNIO方法相比，在具有更高压缩比的同时，准确率也高出2.31%。DIFFO方法准确率高于本文方法0.09%，然而激活位宽仍采用32位浮点数，从后续部署到移动端方面考虑，仍然需要高成本的浮点数乘法器运算和高数据带宽。本文方法权重与激活平均位宽压缩至3.4位，只需要低位宽定点数乘法器和更低的数据传输量便可实现，因此整体上要更优于DIFFO方法。

另选取量化相关工作中常用的Resnet20网络进行量化，量化结果见表1，量化后权重与激活平均位宽仅有4.3位，经量化训练后模型准确率恢复至91.9%，相比于全精度模型仅损失0.99%。相比于PACT方法采用混合精度量化策略，本文方法在量化位宽平均5位时，Resnet20网络的分类准确率要高出此方法0.81%，可以说明本文方法的位宽分配要更加合理。

选取层数较深的ResNet56网络进行实验，量化后权重和激活位宽可压缩至平均3.64位，同时量化后模型准确率达到93.35%，相比于全精度模型准确率损失仅0.48%，所占内存空间只需全精度模型的11.4%。相比于QOCN方法，本文方法的选择的量化策略不仅准确率提高了0.71%，而且压缩比也高于该方法。因为此方法只简单地采用两种量化位宽，难以得到精细的量化粒度，而本文采用2～8位位宽选择，提供多级量化位宽粒度，根据敏感度值可精细分配位宽，可兼顾压缩比与准确率。

3.2 cifar-100数据集上的量化实验

为验证方法的通用性，采用cifar-100数据集继续测试，该数据集共包含5万张训练图片和1万张测试图片，分类结果增加至100种，对比测试Resnet18和Resnet20网络全精度模型和量化后模型分类准确率的变化和量化后的位宽数，实验结果见表2。

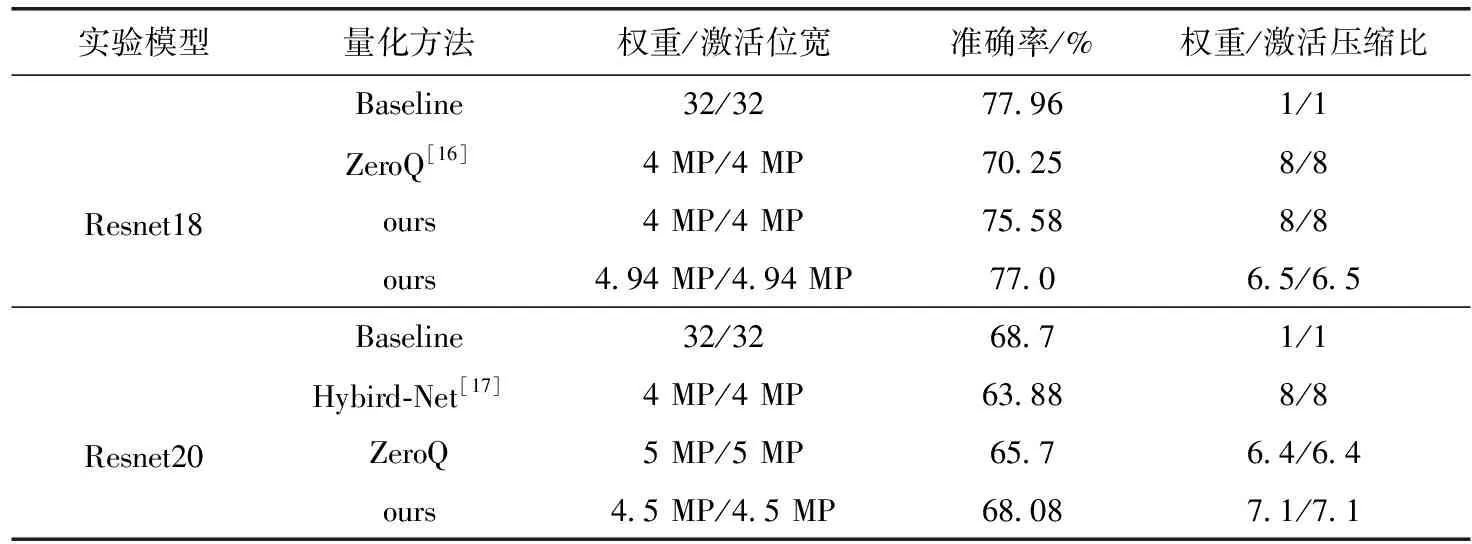
表2 在cifar-100数据上实验结果对比

Resnet18网络权重和激活位宽可量化至平均4.94位，量化后的模型推理准确率达到77.0%。为更直观的与其它方法比较，选取实验过程中一组权重和激活平均位宽量化至4位的策略进行对比分析，ZeroQ方法同样是基于量化层敏感度分析实现混合精度量化，经对比可以看出其分类准确率要远低于本文方法，本文方法选用的敏感度指标对量化层分配的位宽更加合理，在相同压缩比下，准确率高出5.33%。Resnet20网络在cifar-100数据集上量化后权重与激活位宽平均有4.48位，模型准确率恢复至68.08%。与表中ZeroQ方法相比，可以看出本文方法分配的更少的位宽，准确率仍然高出2.38%。与Hybird-Net方法相比，虽然压缩比方面略低，准确率却高出该方法4.2%。

3.3 量化层不同位宽的可视化实验

为验证第1.1节中的结论，进一步说明各量化层中不同位宽带来的差异性，本文选取不同量化位宽方案训练的Resnet20网络，在同一位置可视化输出值并进行对比，结果如图4所示。

图4 不同位宽Resnet20网络量化层输出特征

图中每一行代表不同位宽的网络在同一量化层输出结果，实验选取了网络中3个不同位置比较。可以看出，本文采用混合精度量化图4(c)后的模型，即使在模型不同的位置其输出特征基本与全精度模型图4(b)保持一致，因此保证量化后准确率损失较小。在图4第一、第二行中可以看到，虽然使用不同位宽值，直至量化至3位图4(e)，模型在该层输出基本相同，但是在图4第三行中，从4位模型产生的特征图4(d)区别开始变大，说明统一量化为低位宽会造成模型与全精度模型输出产生较大差异，易造成模型推理准确率的下降。

4 结束语

在本文所述的工作中，我们提出了一种CNN模型混合精度量化的方法，利用敏感度信息和聚类方法极大缩小了搜索空间，并且提出一种自适应策略搜索方案，可以根据目前量化策略结果自行调整搜索状态，逐步调整量化策略。同时重新整合量化训练过程，减少了传统量化训练的计算量，可加快模型训练速度，更高效寻找规定准确率下的最优量化策略。最后在cifar-10和cifar-100数据集上选取不同的CNN模型进行测试，与目前各项主流方法对比，综合各项指标来看，均有提升。但是该方法量化后的模型只完成了在PC端的实验验证，还未实际部署在边缘计算设备上，同时这也是下一步的研究方向，结合FPGA并行计算和可自由配置乘法器及位宽的特点，真正实现CNN模型在边缘设备上的高效应用。