外门空气幕对供暖期高校宿舍室内温度的影响

杨玉昕, 罗 君, 王飞飞, 邱 屹, 葛 航

(1.华中科技大学 环境科学与工程学院, 湖北 武汉 430074; 2.武汉市计量测试检定(研究)所, 湖北 武汉 430050)

1 概述

夏热冬冷地区一般无集中供暖系统,空调器供暖是比较常见的方式。受空调器送风方式的限制,室内温度分布不均,外墙和门窗散热对室内温度的分布有一定影响。

高校学生宿舍作为学生学习、休息的主要场所,环境舒适性对学生健康、学习效率有重要影响[1]。与一般住宅建筑不同,高校学生宿舍的一个房间内一般有多人居住,每位学生均有各自的学习区域,保证宿舍内部不同区域的舒适性水平接近有着重要意义。然而,校内老旧宿舍的节能水平、室内舒适度往往不能满足相关标准和学生需求[2]。传统节能改造不但施工期长、成本高,而且主要目标为提高室内的平均温度,并不能解决温度分布不均的问题。因此,考虑在外门窗上部安装空气幕,以减少外墙和门窗散热量,并改善供暖期高校学生宿舍内温度分布不均问题。

目前,空气幕主要安装在冷库进出口[2]、冷冻陈列柜外侧[3]、建筑出入口[4],减少空气幕内外区域换热作用显著。

有大量研究针对空气幕在烟气扩散控制[5]、污染物扩散控制[6]方面的应用。也有文献研究了空气幕减少外墙和门窗传热的作用。刘泽勤等人[7]在采用上送风上回风方式的空调房间的外窗内侧安装空气幕,将未安装空气幕的空调房间作为对照,对供暖期两种房间的温度场、速度场进行模拟,计算能源利用率。研究表明,增设空气幕可在节能的基础上,提高室内舒适度。

本文以武汉某高校安装空调器、空气幕的4人学生宿舍为研究对象,在供暖期不同室外温度条件下,对人员坐姿时头部所在高度面(1.1 m高度面)的温度场、速度场进行模拟。以1.1 m高度面的空气温度整体水平、空气温度分布均匀性作为评价标准,选取适宜的空调器送风角度。以1.1 m高度面低温(低于23 ℃)区面积比为5%作为评价标准,确定不同室外温度条件下,空气幕最佳送风风速。

2 研究对象与方法

2.1 物理模型

本文以武汉某高校学生宿舍为研究对象,房间几何模型见图1。宿舍为4人间,采用上床下桌布置形式。房间x轴、y轴、z轴尺寸分别为5.0 m、3.3 m、2.9 m。设4个床位,分2组双人床板靠墙布置,每组配置1套储物柜。假设4人均在宿舍并且为坐姿,将人体简化x轴、y轴、z轴尺寸分别为0.4 m×0.2 m×1.2 m的长方体,人体散热量为68 W/人。

房间yOz面为外墙,灰色区域为玻璃外门(通向阳台),y轴、z轴尺寸分别为3.3 m、2.1 m。房间其他面均视为实体内墙。顶棚安装2盏日光灯,始终处于开启状态,发热功率为10 W/盏。

在供暖期,采用壁挂式分体空调器供暖,室内机紧贴房间顶棚安装在玻璃外门上方(水平居中)。回风口位于室内机上边缘与水平面垂直,送风口与水平面夹角45°朝向斜下方,送风口与回风口的长×宽均为0.8 m×0.1 m。空气幕安装在外门上沿,x轴、y轴、z轴尺寸分别为0.2 m×3.3 m×0.2 m,进风口和出风口的长×宽均为3.3 m×0.2 m。储物柜x轴、y轴、z轴尺寸分别为1.45 m×0.87 m×1.75 m,床板x轴、y轴、z轴尺寸分别为4.00 m×0.87 m×0.05 m。人员等效长方体中点x轴、y轴坐标分别为 (1.175 m,0.770 m)、(3.825 m,0.770 m)、(1.175 m,2.530 m)、(3.825 m,2.530 m)。

2.2 数学模型

采用ANSYS Fluent 19.2进行数值模拟,求解的基本数值控制方程包括能量方程、连续性方程、动量方程。采用标准的k-ε模型求解流场,空气假设为不可压缩理想气体,利用boussinesq假设计算由温度梯度引起的自然对流。压力和速度耦合过程采用SIMPLE算法求解,各数值方程采用二阶迎风精度离散格式进行离散。

2.3 网格模型

采用ICEM CFD软件对房间几何模型进行网格划分,在人体表面、风口处等温度梯度和局部风速较大的位置进行网格加密。得到网格数量分别为201 730、797 052、1 187 346的3种网格模型,以室外温度为3 ℃、空调送风速度为3 m/s、空调送风温度为25 ℃为例,模拟房间竖向中心线的温度分布。由模拟结果可知,网格数量为797 052、1 187 346时,模拟结果非常接近,因此网格数量选取797 052。模型网格划分见图2。

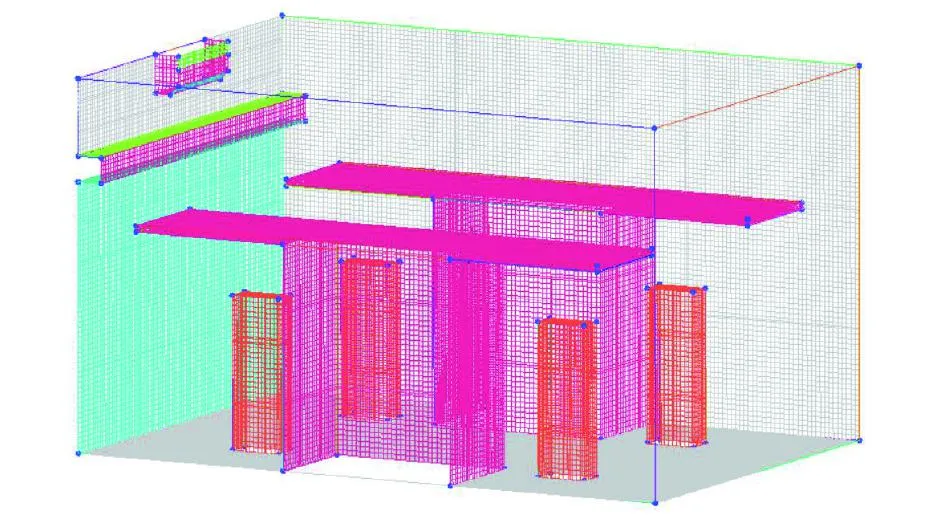
图2 模型网格划分

2.4 边界条件

房间内墙、顶棚、地面均设为绝热壁面,床板、储物柜等家具壁面均设为绝热壁面。外门与外墙的综合传热系数为2.76 W/(m2·K),传热面积按9.57 m2计算,不考虑冷风渗透耗热。

供暖室内设计温度取23 ℃,室内外温差分别选取10、15、20、25 ℃,分别对应室外温度13、8、3、-2 ℃。空调送风温度为25 ℃,送回风速均为3 m/s。空气幕进风、送风风量平衡,内部无加热装置。室内仅有人员及灯具发热。室内空气初始温度为23 ℃。

3 结果与讨论

学生在宿舍环境中多采用坐姿,因此分析人员坐姿时头部所在高度面(1.1 m高度面)的温度、速度分布。

3.1 空气幕关闭

① 空调送风角的影响

在室外温度为3 ℃、空气幕关闭时,模拟空调送风角(送风方向与水平方向夹角,简称送风角)对室内空气温度分布的影响。送风角为0°、45°、90°时,1.1 m高度面的空气温度分布见图3。

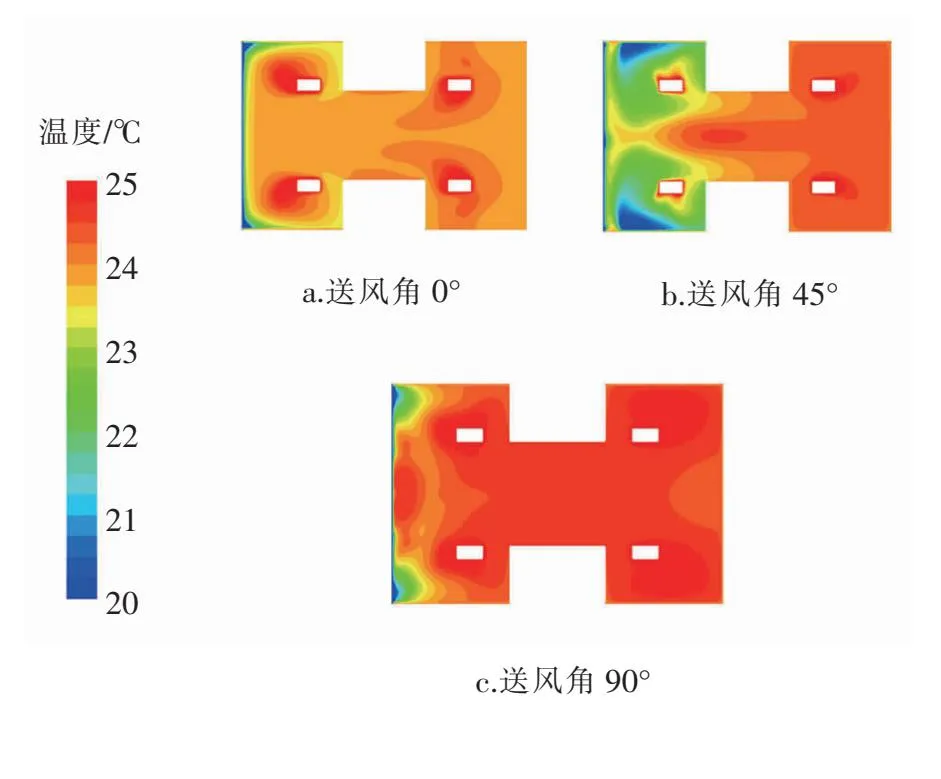
图3 送风角为0°、45°、90°时1.1 m高度面的空气温度分布

由图3可知,送风角为0°时,1.1 m高度面的空气温度整体偏低。送风角为45°时,低温空气区域主要集中在靠近外门一侧,远离外门空间的空气温度比送风角为0°时有所上升。与送风角0°、45°相比,90°时1.1 m高度面的空气温度分布更加均匀,且温度水平有所上升。

在3种送风角中,送风角90°所营造的室内空气温度场最均匀且平均温度最高。但实际中,空调器的送风角度有限,不能实现送风角90°。因此,送风角宜选取45°。

② 室外温度的影响

在送风角为45°、空气幕关闭时,模拟室外温度对室内空气温度分布的影响。室外温度分别为13、8、3、-2 ℃时,1.1 m高度面的空气温度分布见图4。由图4可知,1.1 m高度面上,外门附近的空气温度明显低于远离外门空间的空气温度。随着室外温度降低,低温区域逐渐扩大。当室外温度为13 ℃时,室内主要区域空气温度在23 ℃以上,不需要使用空气幕加以改善。

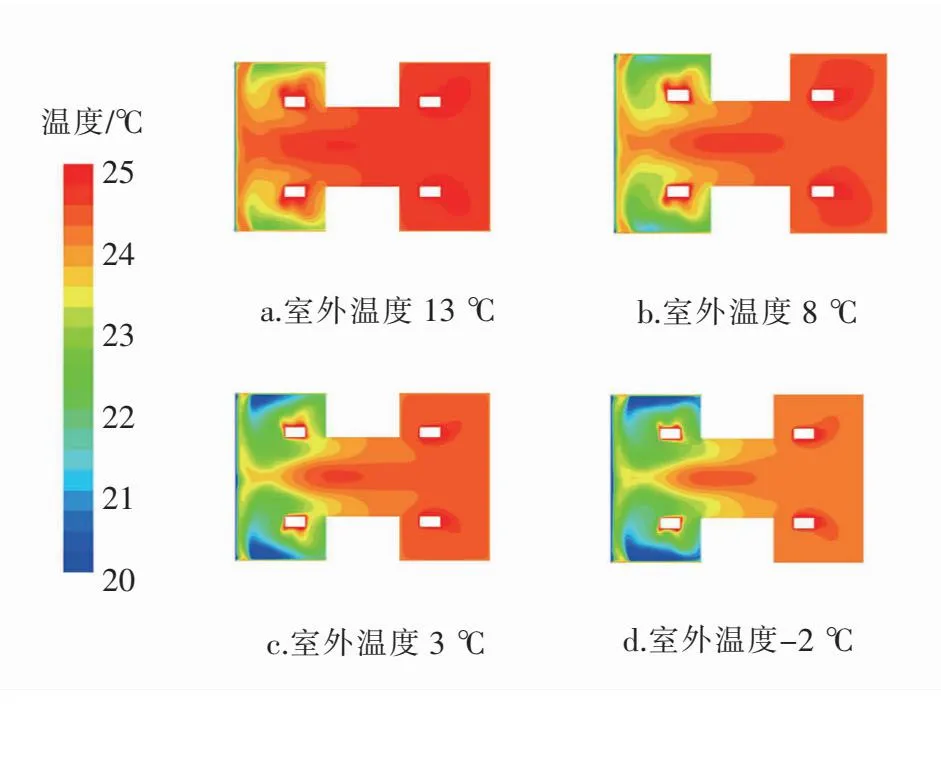
图4 室外温度分别为13、8、3、-2 ℃时1.1 m高度面的空气温度分布

3.2 空气幕工作

在空调送风角为45°、空气幕工作时,模拟室外温度及空气幕送风风速对室内空气温度、速度分布的影响。空气幕送风风速为0.1～1.5 m/s,不同室外温度1.1 m高度面的空气温度分布分别见图5～8。由模拟结果可知,室外温度对室内速度分布的影响比较小,因此仅给出室外温度为3 ℃时1.1 m高度面的速度分布。室外温度为3 ℃时,不同空气幕送风风速1.1 m高度面的空气速度分布见图9。

图5 空气幕送风风速为0.1 m/s时不同室外温度1.1 m高度面的空气温度分布

图6 空气幕送风风速为0.5 m/s时不同室外温度1.1 m高度面的空气温度分布

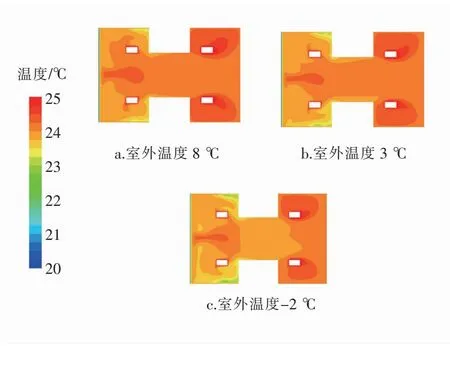
图7 空气幕送风风速为1.0 m/s时不同室外温度1.1 m 高度面的空气温度分布

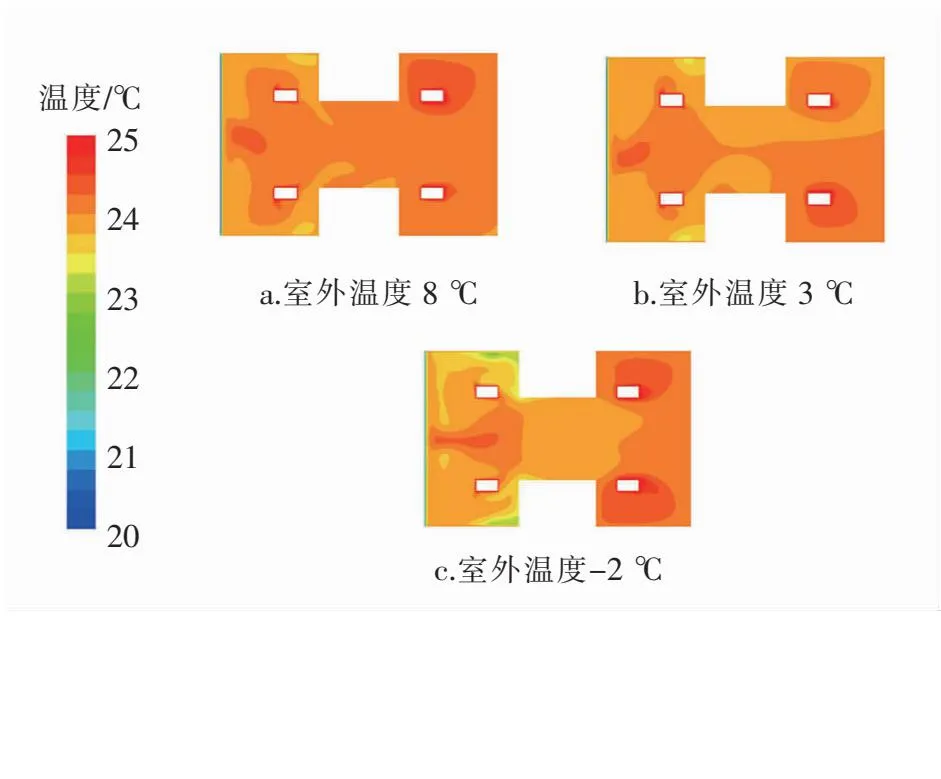
图8 空气幕送风风速为1.5 m/s时不同室外温度1.1 m高度面的空气温度分布

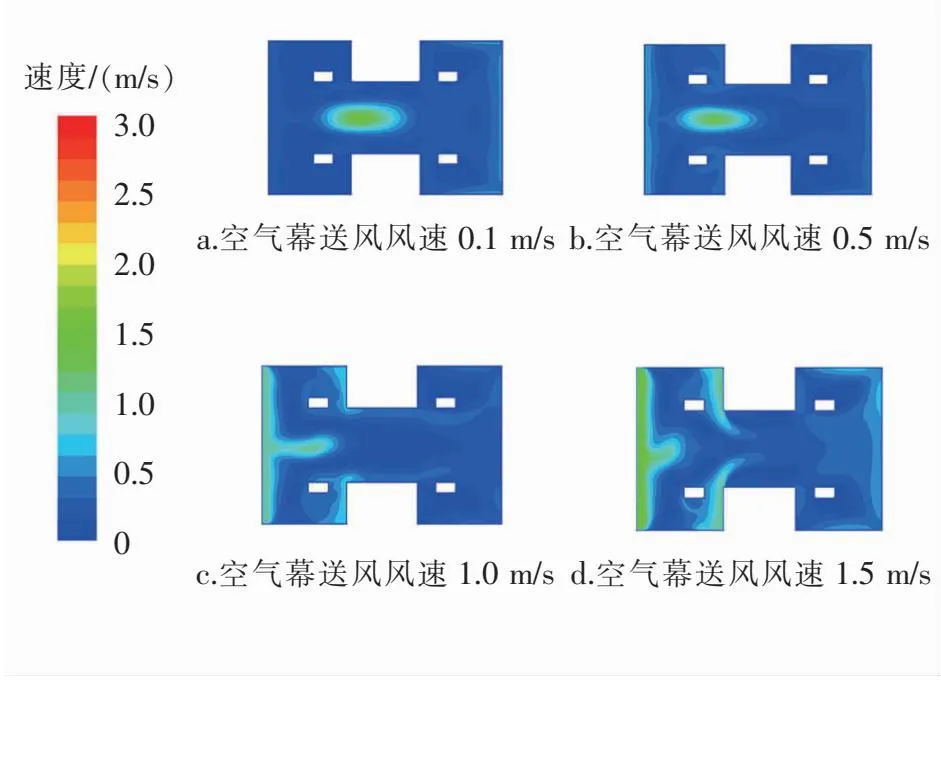
图9 室外温度为3 ℃时不同空气幕送风风速1.1 m高度面的空气速度分布

由图5～8可知,相同室外温度下,随着空气幕送风风速增大,1.1 m高度面空气温度分布更加均匀,增大空气幕送风风速对进一步改善室内空气温度均匀性的作用逐渐减小。

由图9可知,当空气幕送风在较低风速时,1.1 m高度面空气速度分布仍以空调送风为主导,高速区出现在两储物柜中间位置。当空气幕送风风速达到1 m/s后,空气幕送风对1.1 m高度面空气速度分布的影响开始显现,甚至逐渐占据主导地位,坐在外门附近的人员能感到吹风感。

3.3 空气幕最佳送风风速

虽然增大空气幕送风风速有助于室内空气温度分布更加均匀,但空气幕耗电量也随之增大,而且继续增大空气幕送风风速对进一步改善室内空气温度均匀性的作用不明显。

本文以1.1 m高度面低温(低于23 ℃)区面积比为5%作为评价标准,确定不同室外温度条件下,空气幕最佳送风风速。

由模拟结果可知,当空气幕送风风速为0.5 m/s时,不同室外温度1.1 m高度面的空气温度大部分达到甚至高于23 ℃。因此,以0.1 m/s作为步长,模拟计算空气幕送风风速0.1～0.5 m/s范围内1.1 m高度面低温区面积比,见图10。由图10可知,不同室外温度的1.1 m高度面低温区面积比均随空气幕送风风速增大而减小。空气幕送风风速一定时,1.1 m高度面低温区面积比随室外温度升高而减小。

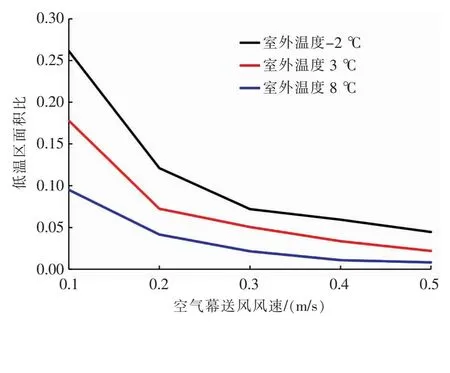
图10 不同室外温度1.1 m高度面低温区面积比随空气幕送风风速的变化

1.1 m高度面低温区面积比为5%时,室外温度8、3、-2 ℃对应的空气幕最佳送风风速分别为0.18、0.30、0.46 m/s。1.1 m高度面的空气速度分布以空调送风为主导,高速区出现在两储物柜中间位置,空气幕送风风速对1.1 m高度面的空气速度分布基本无影响。

4 结论

① 空调送风角宜选取45°。

② 1.1 m高度面低温区面积比为5%时,室外温度8、3、-2 ℃对应的空气幕最佳送风风速分别为0.18、0.30、0.46 m/s。1.1 m高度面的空气速度分布以空调送风为主导,高速区出现在两储物柜中间位置,空气幕送风风速对1.1 m高度面的空气速度分布基本无影响。