高转速柔性转子动平衡设计及研究

洪琪琛，张 川，王 希

（1.中国航发湖南动力机械研究所，湖南 株洲；2.直升机传动技术重点实验室，湖南 株洲）

引言

传动系统是直升机的三大动部件之一[1]，直升机性能在很大程度上取决于传动系统的性能。作为直升机传动系统的重要组成部分，尾传动轴的作用是将主减速器的功率和转速传递给尾减速器，同时补偿输入/输出轴线之间的轴向、径向和角向偏移。

尾传动轴属于空心薄壁转动件，由于设计、制造及安装误差等因素，所有实际转动的中心惯性主轴均或多或少偏移其旋转轴线，此种情况称为转子的不平衡[2]。不平衡会引起转子的挠曲和内应力，使系统产生振动及噪声，加速轴承等零件磨损，降低传动系统工作效率，严重时甚至使转子元件断裂，因此高转速下转子动平衡研究对直升机传动系统的研制和工程应用显得十分必要。

20 世纪50 年代起，国外学者开始对转子的平衡问题展开了广泛且深入的研究。R.E.D.Bishop[3]通过经验总结，进一步发展了振型平衡法，其目标是使转子两端的支承动反力以及各阶的振型不平衡量为零。T.P.Goodman[4]为解决转子质心不在转轴上的问题，对影响系数法进行了全面且系统的论述。针对残余弯曲效应问题，W.L.Meacham[5]等推广了复模态理论方法，但是由于难以得到转子系统较为准确的数学模型，该方法在多数情况下不适用。Artiles A F[6]等研究了瞬态积分对转子系统稳定性的影响，并建立了转子系统运动方程。Ku C[7]等深入研究了阻尼系统对于转子系统的稳定性，研究表明内阻尼增加会导致转子系统失稳。

目前，国内学者对于转子系统的平衡问题也展开了大量研究。林水泉[8]详细介绍了转子动平衡与特点，并对转子动平衡技术的发展趋势作了阐述。张莹，王鲲鹏[9]等人将影响系数法和传递函数法应用于航空发动机柔性转子动平衡，有效降低了不平衡转子的振动。刘红梅[10]等提出将广义回归神经网络和粒子群算法结合的旋翼调整方法，对桨叶的调整参数寻优，可在较少的飞行调整下完成旋翼的动平衡调整。

综上所述，鲜有学者针对高转速下薄壁型柔性转子件的动平衡设计展开研究，因此本文以直升机尾传动轴为研究对象，选取合适的动平衡设计值，并进行振动试验验证，对传动轴的动平衡具有指导意义。

1 动平衡相关概念

当轴系存在偏心距（e）时，轴就会受到此力产生动挠度（γ），当转子的刚性小，转动的角速度较高时，此时动挠度相对于偏心距就会很大，转子发生弯曲变形，根据牛顿第二定律可知：

从图1 可知，当ω/ Ω为0.707 时，挠度γ 恰好等于偏心距e，工程上常以此为界限，即工作转速低于0.707 ω 的转子为刚性转子，高于0.707 ω 的转子则称为柔性转子。一般来说，挠度的存在使得转子沿着一个完全轴线旋转，在支撑处产生交变载荷，易造成转子件疲劳损伤。

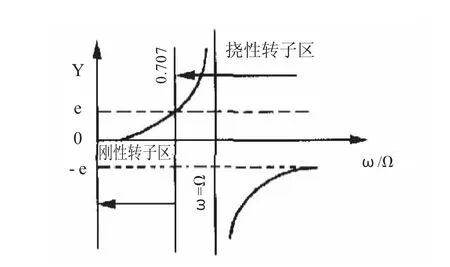
图1 γ 与ω/ Ω关系曲线

由于转子质心与旋转轴线不重合，旋转时转子产生的不平衡离心力为：

式中：n 为转子的转速。

由于离心力的存在，当转子沿着轴线旋转时产生一个空间力系，要想达到动平衡，则需要满足空间力系的平衡条件：

式中：F 表示惯性力；M 表示惯性力产生的力矩。

转子经过动平衡后，不可能将不平衡量完全消除，只能将其降至一个许可程度，经校正后的残余不平衡量称为许用剩余不平衡量（eper）。从式（2）中可知，离心力与转速平方成正比，因各系统轴承承载情况不同，导致确定一个转子的许用剩余不平衡量并非易事。

大量的实践证明，一个转子的许用剩余不平衡量与其自身质量成正比，同类转子各平衡品质等级的转速范围内，许用剩余不平衡量与转子最高工作角速度成反比，计算公式如下：

式中：M 为转子重量；r 为转子校正半径；n 为转子转速；G 为平衡等级。

考虑到技术的先进性和经济上的合理性，1940 年国际标准化组织（ISO）制定了世界公认的ISO 1940平衡等级，分为11 个级别，每个级别之间以2.5 倍为增量，单位为mm/s。对于直升机常用的动平衡等级为G2.5、G6.3、G16 级别等。

2 校正方法

想要转子系统达到平衡，其实就是改变转子的质量分布，使其中心主惯性轴与旋转轴线重合而达到平衡的目的。当测量出转子不平衡的量值或相位后，工程应用上通常有以下校正方法：

（1） 去重法，即在重的一方用钻孔、磨削、錾削、铣削和激光穿孔等方法去除一部分金属。

（2） 配重法，在轻的一方用螺钉连接、铆接、焊接和喷镀金属等方法，即在合适的位置加上一部分金属达到平衡的目的，如图2 所示。

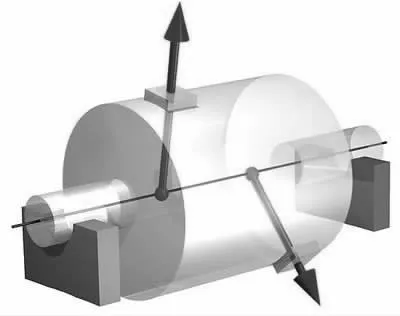
图2 配重法调解动平衡示意

（3） 调整法，通过拧入或拧出螺钉以改变校正重量半径，或在槽内调整两个或两个以上配重块位置；进行热补偿，通过对转子局部加热来调整工件装配状态。

3 某直升机尾传动轴应用

3.1 许用剩余不平衡量计算

某尾传动轴转速约3 300 r/min，质量约为8.4 kg，直径φ134 mm，长度约2 100 mm，按照工程经验，一般可选取G2.5、G6.3 等动平衡等级，本例选取G2.5 级别，尾传动轴为长轴薄壁管且长径比＞5，因此需要选择两个或以上校正面，在两端法兰盘处设置去材料区域，详见图3。

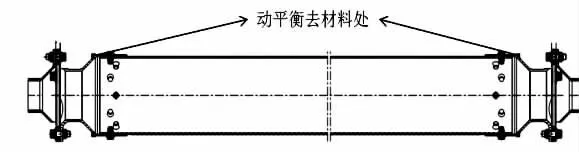
图3 某尾传动轴去材料区域示意

上述参数代入式（5）中计算得许用剩余不平衡量为0.90 g，分配到两端为0.45 g，折算到传动轴半径上的许用不平衡为30.15 g·mm。根据尾传动轴安装状态，动平衡要求为：在三个角向位置（0°、120°、240°）进行动平衡，工作转速下动不平衡量每端≯30 g·mm。

3.2 试验验证

为验证上述动平衡量的合理性，需进行转速试验考核。将被试件安装于试验台上，测试项目主要有转速、振动、位移等，其中转速、振动可通过计算机集中显示和自动采集，在输入/输出端的支座上安装振动传感器，试验过程对振动加速度进行监控；将电涡流位移传感器安装至试验件的1/2 处。试验件安装示意如图4 所示。

图4 试验件安装示意

转速由0 增加至1.155 倍最大工作转速（Nr），验证尾传动轴在最大工作转速的115.5%范围内有无临界转速，振动加速度随转速变化曲线如图5 所示，振动位移随转速变化曲线如图6 所示。

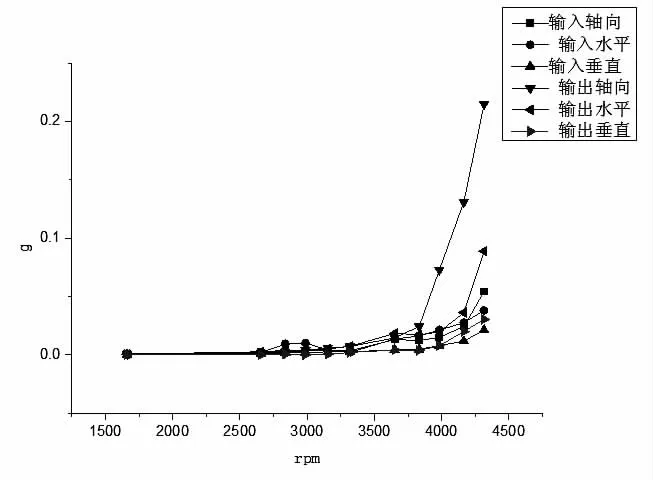
图5 振动加速度随转速变化曲线

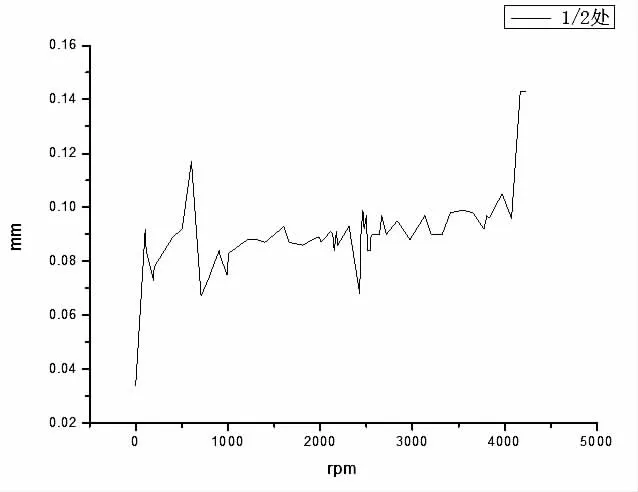
图6 振动位移随转速变化曲线

试验结果表明该尾传动轴振动位移基频响应总体随试验转速增加而逐步递增（最大值约为0.2 g），期间振动位移未出现可识别的基频响应峰值，且没有发现转子过弯曲临界时由自定心导致的相位突变，表明按上述动平衡要求加工后的尾传动轴能够满足振动要求。

4 结论

通过针对转子的动平衡理论研究和试验验证，可得出以下结论：

（1） 在传动轴设计时，动不平衡量要求可根据理论公式进行计算，转速试验结果表明传动轴可满足振动要求，对后续传动轴的设计工作具有指导意义。

（2） 由于尾传动轴组件一般带有膜片联轴节等柔性连接部件，整轴非完全刚性回转体，故理论计算得到的动不平衡量仅供参考，可根据具体结构进行优化，使得平衡工艺更加有效、经济，满足实际工程需要。