基于多特征融合的水工闸门剩余寿命预测

杨 涛,张钰奇,付春健,赵华东

(1.郑州大学 机械与动力工程学院,郑州 450001; 2.河南省智能制造研究院,郑州 450001)

0 引 言

水工闸门由于工作环境恶劣,在运行过程中会不可避免地出现性能退化,最终导致破坏。一旦闸门发生破坏,会造成巨大的经济损失。因此准确预测闸门剩余寿命(Remaining Useful Life,RUL)对于实时评估闸门健康状态,确定合适的维修策略以保证闸门运行安全具有重要意义。

目前研究主要认为锈蚀是影响闸门寿命的最大因素[1]。Kuz’Mitskii等[2]基于锈蚀分阶段模型预测了闸门剩余寿命;李伟康等[3]考虑到锈蚀会影响材料性能,基于D-H曲线对闸门进行RUL预测;然而,目前的研究存在着预测指标单一、精度不高,难以给出剩余寿命的概率分布等问题。

目前,闸门上的锈蚀模型一般为确定性函数,难以体现锈蚀过程的不确定性。而Gamma过程可以很好地模拟锈蚀演化过程[4],体现闸门锈蚀过程的不确定性。因此,考虑采用Gamma过程进行锈蚀模拟,通过数值模拟方法得到闸门退化数据。在获取闸门的退化数据后,同时考虑到工程实际中设备运行工况复杂,反映设备退化的指标往往并不唯一。因此,如何将多种信息进行融合来共同反映设备退化状态,已成为剩余寿命预测的关键。目前,许多研究通过将多种特征融合成健康因子(Health Index,HI)来解决这一问题。任子强等[5]将多维数据融合成一个健康指标来表征发动机的退化过程,提高了RUL预测的精度;赵广社等[6]基于欧式距离构建了健康因子,并对发动机进行了RUL预测。

RUL预测的方法可以大致分为基于数据驱动和退化模型两种[7]。其中,基于退化模型的方法不依赖于大量同类型设备的全寿命周期数据,而是根据历史数据建立退化模型来描述设备的退化趋势,因此得到了广泛的运用[8]。LI等[9]利用维纳过程刻画了涡轮发动机的退化过程;张英波等[10]基于Gamma过程建立了行星架RUL预测模型。

粒子滤波是基于退化模型实现RUL预测的有效手段,在非线性、非高斯系统中具有明显优势。基于粒子滤波的RUL预测方法可以给出剩余寿命的概率分布,改善长期预测的不确定性问题,相较于单一的预测值,更具有参考价值。李玥锌等[11]基于维纳过程对电池退化过程进行建模,并基于粒子滤波算法得到了其剩余寿命概率分布;王玺等[12]基于粒子滤波算法对陀螺仪进行了RUL预测,取得较高的精度。

基于上述分析,本文提出了一种多特征信息融合预测闸门剩余寿命的方法,利用非线性维纳过程对闸门进行退化建模,并基于粒子滤波算法实时跟踪闸门退化曲线并进行RUL预测,同时给出了闸门剩余寿命的概率分布,可以更好地指导工程实际。

1 闸门锈蚀过程模拟

由于闸门运行工况复杂,影响其锈蚀的因素(如水流、干湿循环等)具有不确定性,因此闸门的锈蚀过程也伴随着随机性。此外,锈蚀过程还具有累积性。为了表征锈蚀随时间发展的不确定性和累积性,考虑采用Gamma随机过程模拟锈蚀深度的发展过程。

Gamma过程是一种具有非负增量的随机过程,特别适合模拟具有微小增量的累计渐变过程,如锈蚀、疲劳、蠕变等[13]。假设t时刻的锈蚀量d(t)满足Gamma分布Ga(α(t),β),其概率密度函数为

(1)

式中:d为锈蚀量;α(t)和β分别为形状参数和尺度参数;Γ(α(t))为Gamma函数。

根据Gamma过程的性质,t时刻锈蚀量的均值可以表示为

E[d(t)] =α(t)β。

(2)

当采用Gamma过程描述退化过程时,一般认为尺度参数β为常数,形状参数α(t)与时间的幂成正比[14],即

α(t)=ctb;c>0,b>0 。

(3)

式中c和b均为常数。对于特定退化过程b一般为定值,文献[15] 给出了不同退化类型下b的取值,闸门锈蚀与钢筋锈蚀属于同类,取b=1。

当确定参数b之后,模型中的参数c和β可以结合既有结构的锈蚀观测数据采用极大似然估计法或矩估计法来进行估计。然而,由于缺乏闸门长期锈蚀监测数据,同时考虑到t时刻的锈蚀深度与平均锈蚀速率有关,因此利用已有锈蚀率的统计数据对参数c和β进行反向标定[16],即首先假定参数β为某个固定值,根据式(2)并结合锈蚀速率统计数据即可确定参数c。

当确定参数之后,闸门锈蚀深度发展过程便可以采用Gamma顺序采样法进行模拟:

(1)将总时间T等分为n个子区间。

(2)当t=ti时,生成服从Ga(α(ti)-α(ti-1),β)的随机数Δdi,Δdi便为时段ti-ti-1的锈蚀增量。则ti时刻的锈蚀累积深度为di=di-1+Δdi。

(3)重复以上过程,直至达到总时间T。

2 健康因子的构建

闸门的退化过程可由多种特征参数变化来表示,不同的特征对于闸门退化过程的敏感性不同,并且各个特征之间存在一定的相关性。若将多个特征指标进行单独建模,不仅不符合多变量相互耦合实际情况,也会增加建模的复杂性。因此,对于多特征的情况,常常采用信息融合的方法,利用降维等手段将多维数据转化为一维复合健康指标,这种方法不仅充分考虑了多变量相互关联的情况,也更有利于对闸门退化过程进行建模。因此,将多种特征指标进行融合得到能够表征闸门退化过程的健康因子是进行寿命预测的关键。

2.1 数据获取

闸门锈蚀会使构件截面面积变小,空间结构整体效应发生改变,从而影响闸门的强度和刚度。同时,闸门锈蚀会引起自振频率和振型等模态参数的改变。为此,本文综合考虑了闸门静力学和动力学特性,选取了应力、变形、主梁挠度,“干模态”下前10阶自振频率、位移模态、应变模态,以及考虑流固耦合作用下的“湿模态”前10阶自振频率、位移模态、应变模态,共63种特征指标来共同反映闸门退化过程。

2.2 特征指标筛选

特征筛选是指从特征集中选择出最优的子集来反映闸门退化过程。考虑到单调性强的特征能够很好地表征闸门的退化趋势,因此首先对特征进行单调性筛选。Spearman相关系数可用于评估2个变量之间相关关系的程度,考虑到时间序列是严格单调的,因此计算每一种特征时序与对应时间序列的Spearman作为该种特征的单调性得分。同时,考虑到变化程度大的特征能更好地反映退化过程。因此,综合考虑单调性和离散性对特征指标进行筛选。

对于某一特征参数序列X=(x1,x2,…,xn),相应的时间序列T1=(t1,t2,…,tn),则:

(1)单调性指标为

(4)

式中:n为数据的个数;分别将X,T1中的元素按照从小到大的顺序编秩;Ri表示xi在X中的秩次;Qi表示ti在T1中的秩次。

(2)离散性指标为

为发现最优特征指标,首先选择出单调性较强的特征指标,然后再对离散性高的特征指标进行选择。

2.3 特征融合及健康因子的构建

多特征参数可以很好地表征设备退化状态,也会使设备建模和数据处理复杂化。因此,要将多维数据融合成一维数据,即通过采用健康因子来表征闸门的退化过程。

主成分分析(Principal Component Analysis,PCA)是一种数据融合和特征提取的重要方法,主要思想是通过寻找一组正交基,将高维特征映射到低维空间,从而达到降维的目的。其主要步骤为:

(1)将性能退化指标构成特征数据矩阵Y为

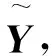
(7)

(3)计算P的特征值m1,m2,…,mp并从大到小进行排序,计算对应的特征向量e1,e2,…,ep。

(4)根据特征值mq,计算第q个主成分对应的贡献率

(8)

一般取贡献率ξ>80%的主成分可以较全面地反映出特征的信息[17],将其当做特征融合后的健康因子来反映设备退化过程。

3 闸门寿命预测

3.1 粒子滤波原理

粒子滤波是一种基于蒙特卡洛(Monte Carlo,MC)理论的贝叶斯估计算法,可用于处理非线性、非高斯系统的状态估计问题。贝叶斯算法是粒子滤波的基础,通常采用状态转移方程和观测方程来描述系统的状态空间

(9)

式中:xk-1、xk分别表示k-1和k时刻系统的状态值;fk表示系统的状态传递函数;εk-1表示系统的过程噪声;yk表示k时刻系统的观测值;hk表示观测函数;vk表示系统的测量噪声。

贝叶斯滤波是对系统的后验分布进行求解,首先根据状态转移方程,根据k-1时刻的观测值,可预测得到k时刻系统状态的先验分布

p(xk|y1:k-1)=

(10)

式中:p(xk|xk-1)由状态转移方程定义;y1:k-1为1:(k-1)时刻的系统观测值。

在此基础上,根据k时刻观测值,利用贝叶斯理论得到k时刻的后验概率密度分布

式中p(yk|xk)由状态测量方程定义。

由式(10)、式(11)可知,上述过程存在着复杂的积分运算,往往难以得到精确解。为了解决上述问题,粒子滤波算法借鉴蒙特卡罗方法将k时刻的后验分布离散加权为

(12)

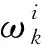
由式(12)可知,得到粒子对应的权值分布,就可以实现对状态概率分布的近似估计,假设q(x0:k|y1:k)表示过去时刻状态的后验估计,同时状态和观测信息遵循一阶马尔科夫过程,则序贯重要性采样粒子权重可转换为

(13)

然而,随着迭代次数的增加,权重有可能只存在少数粒子中,大部分粒子的权重可能小到忽略不计,造成估计性能的下降。因此,常常通过采用重采样方法降低粒子退化问题。

3.2 退化模型的建立

闸门在运行过程中由于工作环境恶劣,其退化过程呈现出明显的不确定性。Wiener过程可以很好地描述复杂设备退化过程中的不确定性,在RUL预测中得到了广泛运用。考虑到以上因素,利用非线性维纳过程来刻画闸门随机退化过程,即

X(t)=X(0)+λeθt+σBB(t) 。

(14)

式中:X(t)表示t时刻的系统状态;X(0)为系统初始状态;λ为漂移系数;eθt为时间t和参数θ的非线性函数,用于表示退化过程中的非线性;σB为扩散系数;B(t)为标准维纳过程。

因此,闸门的退化过程可以描述为

xk=xk-1+λk-1(eθk-eθ(k-1))+ηk。

(15)

式中ηk=σB(B(tk)-B(tk-1))服从于正态分布N(0,σ2Δt),Δt=tk-tk-1。

事实上,由于测量结果与真实状态之间不可避免地存在误差,因此,测量状态和真实状态之间的关系可以表示为

yk=xk+v。

(16)

式中v为测量噪声,服从于正态分布N(0,γ2)。

同时,由于过程噪声可以由其他参数的不确定性实现[18]。因此,根据退化模型可以得出其状态空间模型,即

由式(17)可得,利用Yk=[xk,λk,θk,σk,γk] 可表示出系统的状态,并结合第3.1节所叙述的粒子滤波原理,利用在线数据实时更新未知参数,便可以实现RUL预测。

3.3 剩余寿命预测

在得到状态空间方程之后,根据第3.2节所述的粒子滤波算法对模型参数进行更新,可以得到t时刻的系统状态,根据退化模型进行递推,可以对t+φ时刻的系统状态进行预测[19]。退化模型递推公式为

1≤ζ≤φ。

(18)

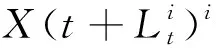
图1 RUL预测示意图Fig.1 Schematic diagram of RUL prediction

4 案例验证

4.1 有限元模型建立

某溢洪道露顶式弧形钢闸门尺寸为12 m×10.5 m(宽×高),主要材料为Q345B,弹性模量取2.06×105N/mm2,密度取7 850 kg/m3,泊松比取0.3,作用水头取9.4 m,主梁计算跨度为7.6 m,现场原型如图2所示。闸门为空间薄壁结构,采用Shell181壳单元模拟。闸门湿模态仿真时,上游水体长度取超过闸门高度10倍的长度,取150 m,采用Fliud30单元模拟,水流和闸门的相互作用表现在闸门迎水面上,将其设为流固耦合面。

图2 闸门现场Fig.2 Site photo of the gate

4.2 闸门锈蚀深度演化过程模拟

根据文献[20] 提出的锈蚀线性模型,闸门上的锈蚀深度变化可根据式(19)计算,即

(19)

式中:dL(t)为闸门t时刻的锈蚀量;t为闸门运行年限;v0为锈蚀速率;tI为闸门开始锈蚀的年限,一般取3～7 a,本文取5 a。

闸门上的锈蚀分为全面锈蚀和局部锈蚀,根据工程实际,全面锈蚀常常发生在面板、支臂、纵梁、肋板、次梁等结构上,局部锈蚀常常发生在下主梁积水处、面板边侧和边梁漏水处。根据统计我国闸门锈蚀速率的均值在(0.015～0.070)mm/a范围内,考虑面板和局部锈蚀区域与水长期接触,因此对面板和局部锈蚀区域锈蚀速率取v1=0.07 mm/a,对于支臂、纵梁等其他区域取v2=0.06 mm/a。

假定尺度参数β=0.1,结合式(2)、式(19)便可以得到形状参数α(t)为

α(t)=c(t-5),t>5 。

(20)

式中:v1=0.06 mm/a时,c=0.6;v2=0.07 mm/a,c=0.7。

确定形状参数α(t)和尺度参数β后,便可以利用Gamma顺序采样法模拟闸门锈蚀发展过程。值得说明的是由于锈蚀过程存在着不确定性,利用Gamma顺序采样法会产生多条锈蚀曲线,通过实际检测的锈蚀数据的增加,利用参数估计方法可减少这种不确定性。为了数据的可重复性和合理性,本文采用了设置随机种子的方法,找到与线性模型相近的曲线,既能保证其锈蚀过程的不确定性,又保证其合理性,得到的锈蚀发展过程如图3所示。图3中线性增长模型为文献[20] 提出的锈蚀模型,其无法体现锈蚀过程中的不确定性;考虑锈蚀深度发展过程的不确定性,利用Gamma过程模拟锈蚀深度发展过程时,其是由一系列不同长度的微小增长段构成。

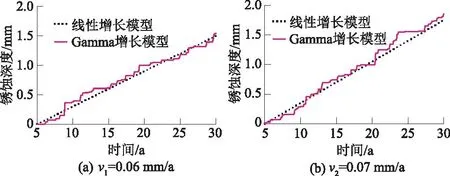
图3 锈蚀深度演化过程Fig.3 Evolution process of corrosion depth

根据文献[21] ,当最大应力发生处厚度≤16 mm时,取[σ] =225 MPa。通过对不同运行年限下的闸门进行仿真,结果表明在29 a时闸门上最大应力σmax>0.95[σ] =213.75 MPa达到失效的条件,图4为闸门失效时刻应力云图。

图4 闸门应力云图Fig.4 Stress contours of gate

4.3 闸门特征指标筛选

利用第2.2节所叙述的单调性和离散性指标对特征进行筛选,特征指标得分如图5所示。图5中横坐标1～3分别为应力、变形、主梁挠度,4～33分别为干模态下前10阶自振频率、位移模态、应变模态,34～63分别为湿模态下前10阶自振频率、位移模态、应变模态。

图5 特征指标得分Fig.5 Scores of characteristic indices

综合考虑,先取单调性得分>0.9的特征指标,然后再从单调性筛选之后的指标中进行离散性筛选。考虑到10阶之后的离散性得分趋于平稳且数值较小,对健康因子的构建影响不大,因此取离散性得分前10特征用于融合健康因子,共筛选出应力、变形干模态下3、4、5、8阶位移模态,湿模态下4、5、8阶位移模态,5阶应变模态在内的10种特征,10种特征的退化曲线如图6所示。闸门所筛选出的变形、位移模态、应变模态等特征的初始状态云图如图7所示。(由于应力图4已给出,本处不再列出)。

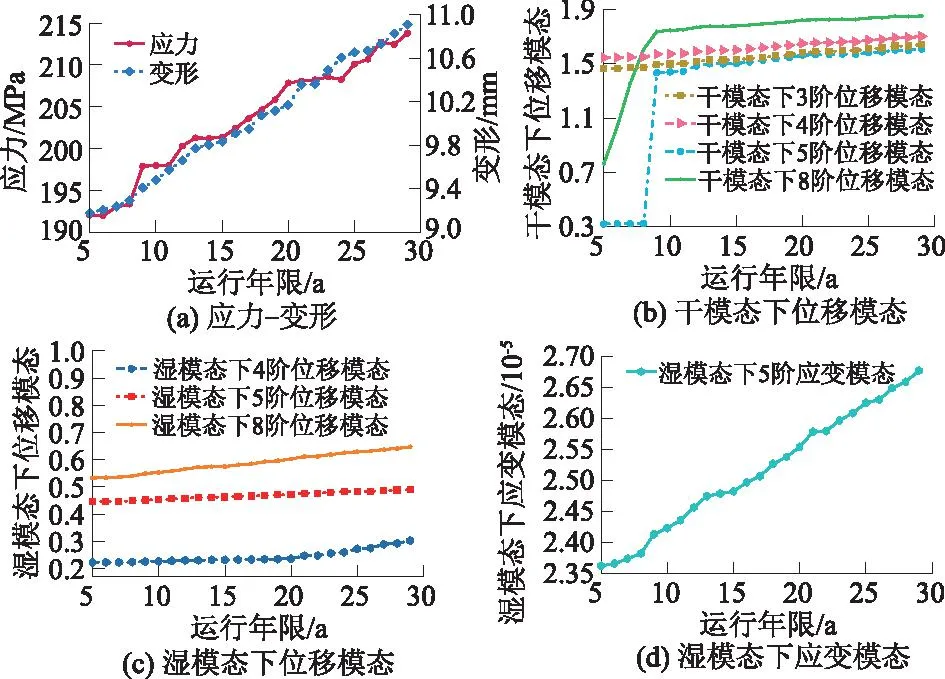
图6 特征指标退化曲线Fig.6 Degradation curves of feature indices

图7 特征指标云图Fig.7 Contours of feature indices

4.4 闸门健康因子的构建

根据2.3节所论述的PCA方法对筛选后的特征进行融合以构建健康因子,利用PCA方法得到的各主成分分量得分如图8所示。

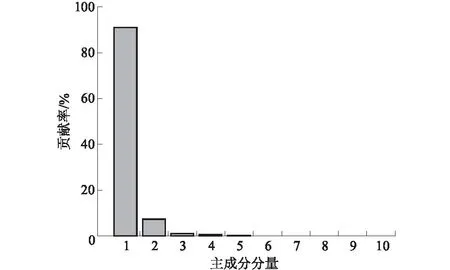
图8 各主成分贡献率Fig.8 Contribution rate of each principal component

其中,第一主成分贡献率ξ=90.960 1%,满足ξ>80%的要求,因此,取第一主成分构建健康因子,健康因子曲线,如图9所示。

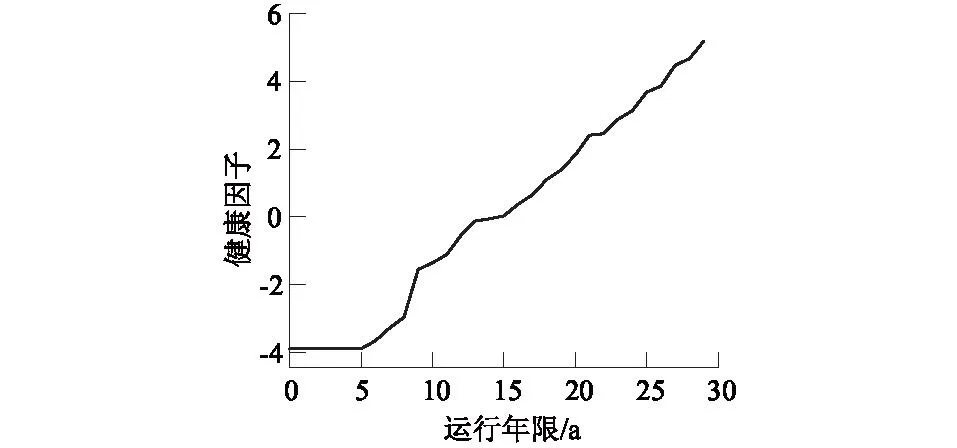
图9 健康因子曲线Fig.9 Health index curve

4.5 闸门剩余寿命预测

在得出健康因子退化曲线之后,便可以利用粒子滤波方法实时跟踪退化曲线,并进行RUL预测。在利用粒子滤波方法进行寿命预测前,需先确定粒子的初始分布。然而事实上,对于一个特定的系统很难进行足够多的寿命测试以获取可靠的参数先验分布[22]。因此,参数的先验分布一般是根据经验得出,通过对闸门腐蚀退化过程进行反复试验并结合先验知识,发现初始分布为均匀分布更加符合闸门退化过程,具体参数如表1所示。

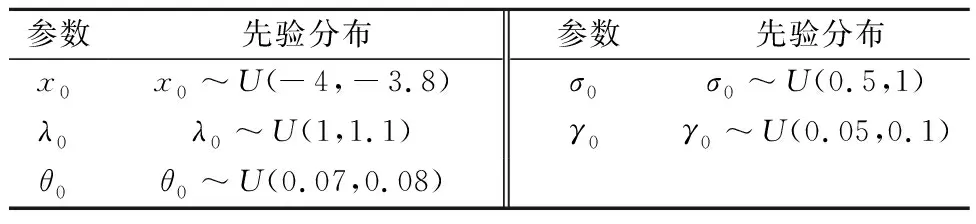
表1 初始参数分布Table 1 Initial parameter distribution

利用第3.1节所叙述的粒子滤波原理对闸门进行RUL预测,由于粒子滤波中的粒子是从初始分布中随机产生的,导致每次循环预测结果在微小范围内波动。为了更好地说明粒子滤波进行RUL预测的原理和步骤,图10—图12是粒子滤波单次循环预测的结果。粒子滤波实时跟踪退化曲线如图10所示,由图10可以看出所提方法能很好地跟踪退化曲线,并能有效地预测闸门RUL。

图10 实时跟踪退化曲线Fig.10 Tracking of degradation process

状态跟踪集(即不同的预测时刻)和粒子数是衡量粒子滤波算法有效性的关键参数。表2为算法在不同的组合方案下的仿真,仿真次数为100次,从表2可看出在不同组合方案下,该算法的预测精度均较高,表明该算法具有较强的稳定鲁棒性、泛化适用性。

表2 不同组合下RUL预测结果对比Table 2 Comparison of RUL prediction results under different combinations

综合考虑预测精度和时效性,将粒子数设为1 000,则在每一个预测时刻可以得到1 000个RUL预测值,从而得出RUL分布直方图,部分预测时刻的RUL分布频率直方图如图11所示。将粒子滤波预测中值当做预测值,由图11可知,在95%的置信区间内,预测值与真实值吻合程度较高。随着闸门运行年限的增加,在不同预测时刻可以得到预测的剩余寿命概率密度函数,如图12所示。从图12可以看出,随着闸门运行年限的增加,剩余寿命的概率分布区间范围在逐渐减小,说明预测的不确定性在逐渐降低。

图11 剩余寿命分布直方图Fig.11 Histogram of RUL distribution

图12 剩余寿命概率密度函数Fig.12 Probability density function of RUL

4.6 RUL预测结果及分析

为了验证所提算法的稳定性以及预测性能的优劣水平,对每一预测时刻进行100次重复试验。同时为了更好地指导工程实际,给出了各个预测剩余寿命区间出现的概率,部分预测时刻结果如表3所示,表3中预测值是指100次循环下预测RUL的均值,Var是指100次循环下预测RUL的方差,AE代表预测值与实际RUL的绝对误差。

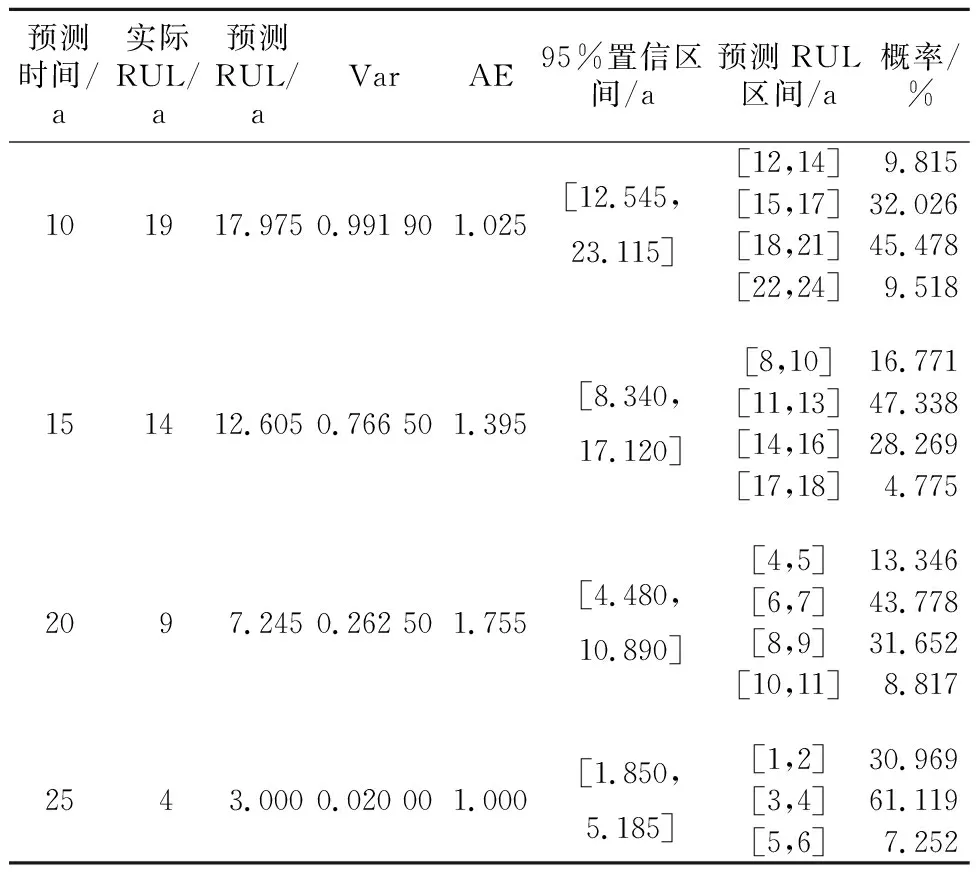
表3 100次重复试验结果Table 3 Results of 100 replicate tests

从闸门运行第10年开始预测,按照上述方法可得到闸门不同运行年限下的RUL预测结果,如图13所示。由图13可以看出,RUL预测结果与实际RUL结果相近,且真实RUL均在95%的预测RUL置信区间内。

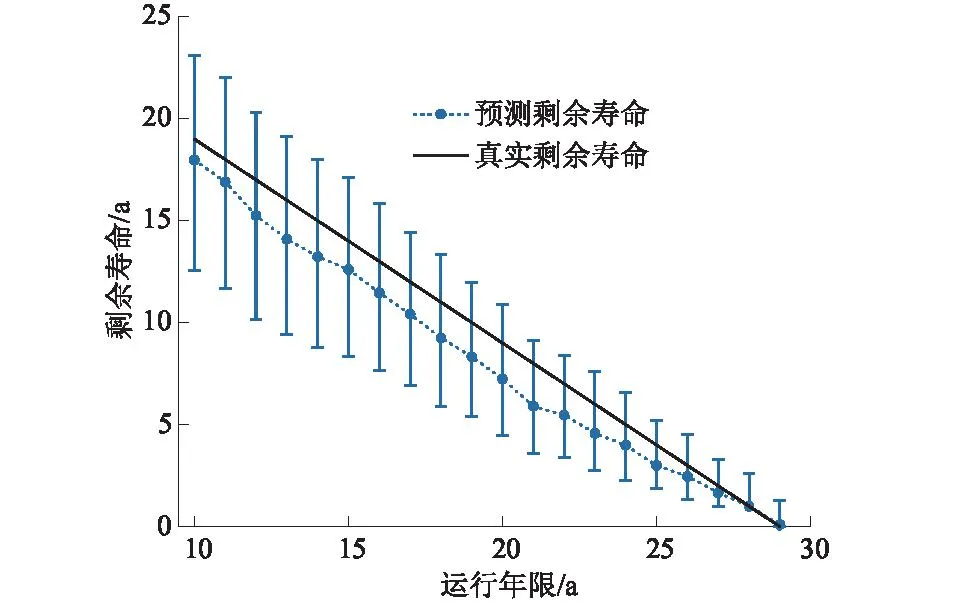
图13 剩余寿命预测结果Fig.13 RUL prediction results

为了客观衡量预测的精度,引入均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)和方差绝对误差(Variance Absolute Error,VAE)来进行评价(式(21)),评价指标得分越小说明预测的精度越高,结果如表4所示。从表4可以看出3个评价指标得分均比较小,说明所提方法预测闸门RUL具有较高的精度。

表4 评价指标得分Table 4 Scores of evaluation indices

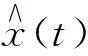
5 结 论

(1)利用应力、自振频率、位移模态、应变模态等多特征参数相较于单一指标更能全面、准确地反映闸门退化过程。

(2)利用非线性维纳过程对闸门退化过程进行建模,并基于粒子滤波对其进行剩余寿命预测,可以得到剩余寿命的概率分布以描述预测结果的不确定性,从而更好地指导闸门日常管理。同时,由评价指标RMSE为1.395 5,说明所提方法具有较高的预测精度。

(3)未来根据剩余寿命预测结果,综合考虑经济性、安全性等因素以确定合理的维修策略是下一步研究的关键。