时间-温度-应力等效原理在PET蠕变拉伸中的应用

李智勇

(湘潭大学土木工程学院)

聚对苯二甲酸乙二醇酯（Polyethylene tere‐phthalate，PET）是一种黏弹性高聚物，由于其质量轻、耐高温等优点被广泛应用在建筑材料、机械制造等领域。PET 材料在实际应用时会经历长时间的静态储存，这一过程中温度和载荷的作用使PET 产生一定的蠕变变形。长期蠕变会使PET 材料的使用性能受到影响，导致材料提前失效。研究PET 长期蠕变变形的演化规律，有助于在工程中安全地使用其材料，降低事故的发生。

对于PET 材料的蠕变性能的研究，Wu 等[1]利用数字图像相关法（Digital Image Correlation，DIC）对钻孔增强PET 材料进行蠕变拉伸，使用Findley 模型分析了PET 在高温下的短期蠕变行为。Yeo 等[2]采用阶梯等温法（SIM）对PET材料的蠕变性能进行测试，结果表明PET蠕变第一阶段的应变速率与施加荷载无关，基于蠕变实验数据通过四参数的Weibull 模型预测其长期蠕变行为。Moghaddam 等[3]对PET 改性沥青进行不同温度和不同应力水平下的蠕变实验，利用三阶Zhou 模型对混合料的蠕变第一、第二阶段进行描述。黏弹性材料的力学性能与温度、应力水平、老化等因素相关，对于黏弹性材料长期力学性能的演化，研究人员大多应用时间-温度-应力等效原理来研究这一现象，利用实验室内短期实验数据来预测其实际工程状况下的长期力学行为。Brostow[4]研究温度、应力对分子链松弛能力的影响，得出了时间-温度-应力等效原理，并给出应力移位因子的方程式。罗文波等[5]考虑了温度和应力对材料自由体积的影响，基于WLF 方程，提出了温度-应力联合因子，并给出了温度-应力联合移位因子的表达式。张建伟等[6]对丁腈橡胶进行了不同温度和不同应力下的热处理实验，采用时间-温度-应力等效原理对温度和应力对丁腈橡胶热处理加速效果进行描述。赵龙等[7]对PBX材料进行了不同温度下和不同梯级应力下的蠕变拉伸实验，发现时间-温度-应力等效原理可以较好的描述PBX的蠕变行为。Wang 等[8]考虑到物理老化和流变损伤等因素对PMMA 长期蠕变性能的影响，推导了一种包含损伤因子的时间-温度-应力叠加原理表达式。

对此，本文以PET材料作为研究对象，对PET材料开展了不同温度、应力下的蠕变拉伸实验。研究时间-温度-应力等效原理在PET 材料中的适用性，得到恒温度应力移位因子和恒应力温度移位因子，从而构成在参考状态下的蠕变柔量主曲线来表征PET 材料的长期力学性能。此方法对分析PET 材料非线性黏弹性力学行为和预测其使用寿命有重要意义。

1 时间-温度-应力等效原理

Willimas[10]根据自由体积理论提出WLF 方程用来描述高聚物的时间-温度等效原理，认为材料的自由体积分数f和温度T的改变存在着线性关系：

式中：φT为材料的热膨胀系数，f0为材料在参考温度T0下的自由体积分数。存在时间-温度移位因子αT=η/η0=τ/τ0，η0、τ0分别为参考温度下材料的粘度和松弛时间，使得：

将式⑴带入式⑵得到移位因子的表达式为：

式中C1，C2为材料常数，这便是广泛应用于黏弹性材料力学行为温度相关性研究的WLF方程。

而罗文波等[12]发现应力水平也会对材料的自由体积产生类似的影响提出了时间-温度-应力等效原理，即：

式中：φσ为材料的应力膨胀系数，σ0为参考应力。存在温度-应力联合移位因子αTσ使得：η(T，σ) =η(T0，σ0)αTσ，结合式⑶和式⑷得到温度-应力联合移位因子的表达式为：

当应力为恒定值，式⑸退化为式⑶。除此之外还存在恒应力温度移位因子和恒温应力移位因子有：

根据时间-温度-应力等效原理，材料在温度T0、应力σ0、t时刻下的蠕变柔量可以用温度T、应力σ、t/αTσ时刻的柔量值表示即：

因此可以用较高温度、应力下的短期蠕变实验来预测材料在较低温度、应力下的长期蠕变行为。

2 蠕变实验

2.1 试验材料与设备

实验所使用的PET 材料来自广东省东莞市兴燕塑业有限公司。样品通过静压加工成矩形条样品。PET材料的试样尺寸为：长150mm，宽15mm，厚2mm。

实验仪器由配备恒温箱的M-3000 电磁式疲劳试验机，恒温箱的控温精度为±1℃，M-3000 的载荷量程为0.01N～3000N，载荷精度为显示值的±0.05%，最大位移限值为25mm，位移精度为±0.01mm。

2.2 试验方案

对PET 分别进行恒温不同应力和恒应力不同温度下的蠕变实验，在进行蠕变实验前将PET 试样置于恒温箱保持1h，恒温时间到达后将应力伺服至0然后开始蠕变实验，设置蠕变时间为1h，荷载加载速率为50N/s。

3 结果与讨论

3.1 温度对蠕变柔量的影响

通过恒应力不同温度下的蠕变实验考察温度对蠕变变形的加速作用，同时验证时间-温度等效原理在PET 材料中的适用性。在13.3MPa 和16.0MPa 下对典型温度(26℃，30℃，34℃，38℃，42℃)下的PET 材料进行3600s 的短期蠕变实验，结果如图1 所示。可以发现温度对PET 的蠕变性能有着明显的影响，温度越高，蠕变变形越大，材料的蠕变速率随着温度的升高而增大，随着时间的增长蠕变速率减弱然后进入稳态期。

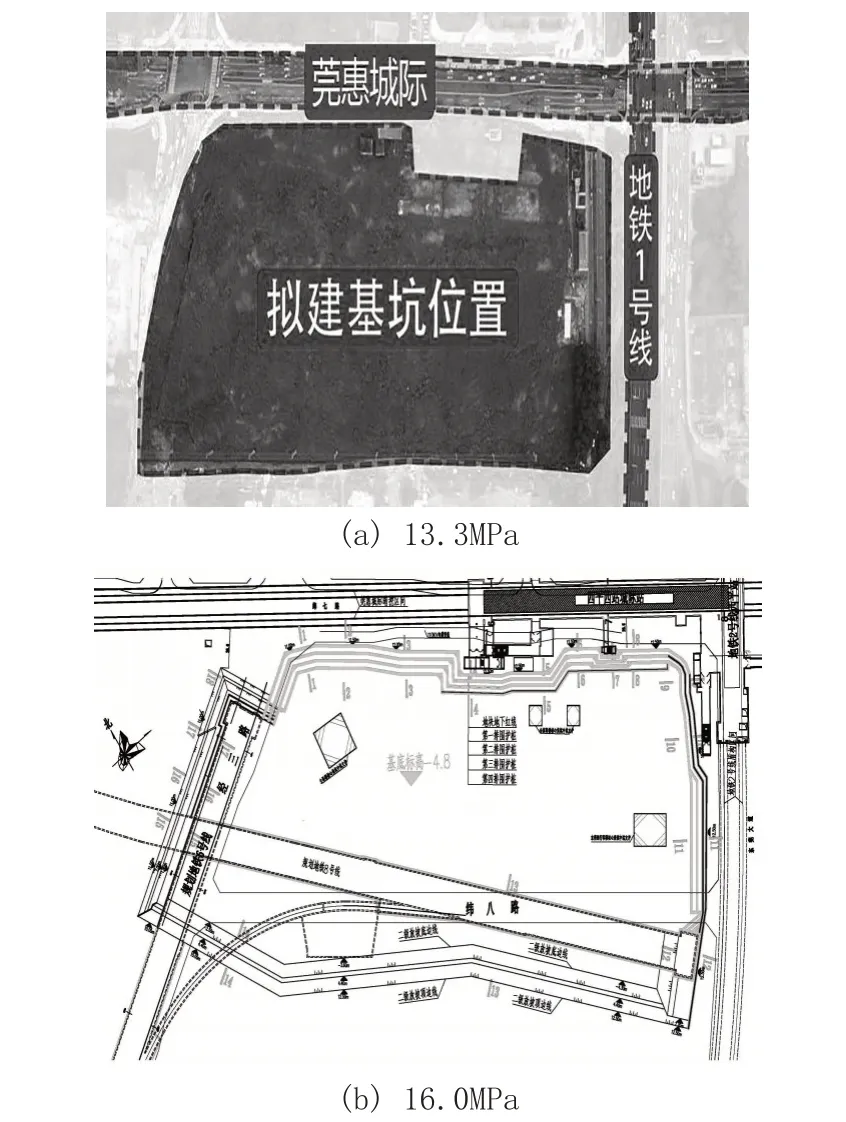
图1 不同温度下的PET蠕变柔量曲线

3.2 应力对蠕变柔量的影响

为考察应力对PET蠕变性能的影响，在30℃和34℃下对PET 材料进行不同应力水平(13.3MP℃，14.6MPa，16.0MPa，17.3MPa，18.6MPa）下的蠕变实验。由图2 可以看到，应力也会加速PET 的蠕变变形，随着应力水平的增大PET 的蠕变柔量增长速率增加，这表明在本实验研究的应力范围内，PET呈明显的非线性特征。

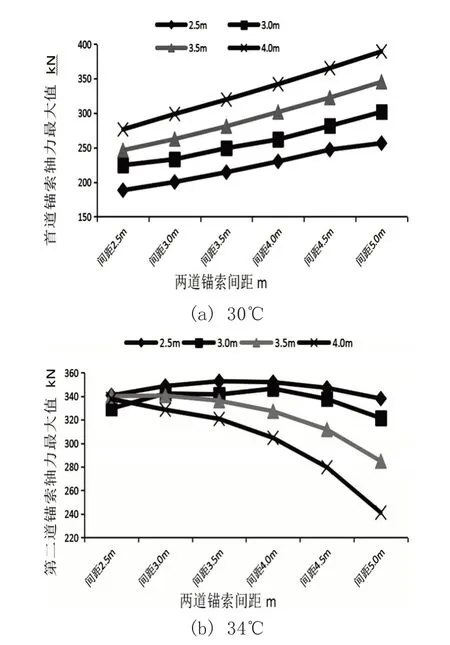
图2 不同应力水平下的PET蠕变柔量曲线

3.3 时间-温度等效原理构建蠕变柔量主曲线

对PET 进行时间-温度等效性分析时，以T0=30℃作为参考温度，将图1 中其他温度下的蠕变柔量曲线向参考曲线平移,移位距离为相应温度的移位因子。最终获得恒应力参考温度下的蠕变柔量主曲线如图3 所示，温度移位因子logαT见表1。从图中可以看出，在对数时间坐标轴上平移后，蠕变柔量曲线簇形成一条光滑的主曲线，主曲线的时间跨度与试验时间相比显著增长，13.3MPa 下的蠕变柔量曲线在参考温度T0=30℃交汇后时间尺度接近105s，除此之外，从表1 可以发现，不同应力下相同温度的移位因子不同。

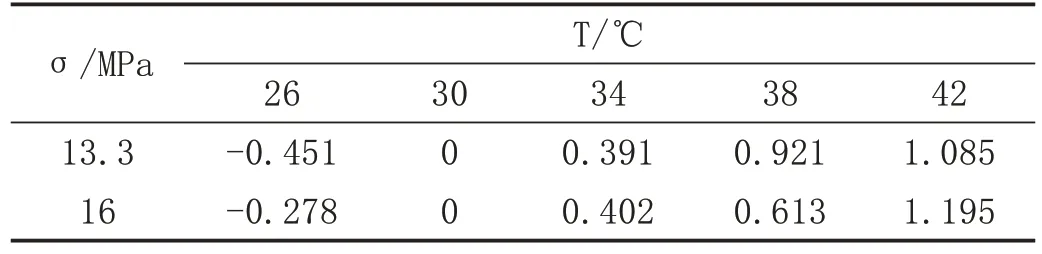
表1 恒应力下PET温度移位因子log αT

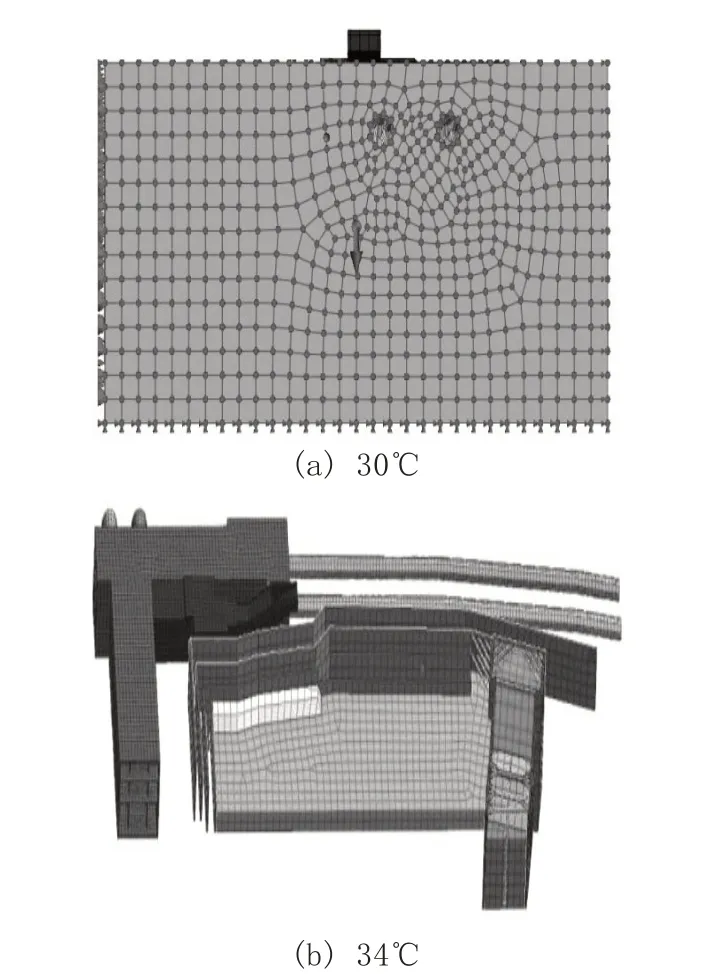
图3 PET在13.3MPa下的蠕变柔量主曲线

图3 PET在30℃下的蠕变柔量主曲线

3.4 时间-应力等效原理构建蠕变柔量主曲线

对30℃和34℃不同应力下PET 的蠕变柔量曲线进行时间-应力等效性分析，以σ0=13.3MPa 的蠕变柔量曲线作为初始主曲线，将2 中其余应力下的蠕变柔量曲线按照应力从低到高的顺序依次平移并更新主曲线，移位距离为相应应力的移位因子，最终获得恒温度参考应力下的蠕变柔量主曲线如图4 所示，计算得到的应力移位因子logασ见表2所示。

图4 不同移位顺序的蠕变柔量主曲线

3.5 时间-温度-应力等效原理在PET 中的适用性

单一的时间-温度等效和时间-应力等效原理在PET 中有很好的适用性，为验证时间-温度-应力等效原理，可以将两条恒力不同温度柔量主曲线和两条恒温不同应力柔量主曲线放入同一坐标系进行耦合对比。为了减少主曲线的数量，以T0=30℃，σ0=13.3MPa 作为参考温度和参考应力，将两组主曲线进一步移位得到同一条件下的主曲线。

将不同移位顺序的两条主曲线绘制在同一坐标系中，得到温度应力耦合蠕变柔量主曲线，如图5 所示。可以发现，恒温蠕变柔量主曲线和恒应力蠕变柔量主曲线在图中相同的时间坐标内重合度较好，整体曲线较光滑，耦合后的主曲线时间尺度与先温度移位后应力移位的主曲线相当。这一结果表明，时间-温度-应力等效原理在PET中依然有很好的适用性，20条蠕变柔量曲线交汇形成的耦合柔量主曲线表现出一致的变化规律。

图5 温度-应力耦合蠕变柔量主曲线

3.6 移位因子比较

要想将力学曲线对任意温度T0和应力σ0下移位，需要求得温度-应力联合移位因子。计算温度-应力联合移位因子的方法有三种：⑴直接将其他试验条件下的蠕变柔量曲线向参考温度、应力下的曲线平移，由Matlab 曲线移位函数计算得到移位因子。⑵先进行恒力不同温度移位求得温度移位因子，再进行恒温不同应力移位求得应力移位因子，两者之和为联合移位因子⑶先求得恒温应力移位因子，再求得恒力温度移位因子，两者之和也为联合移位因子。用公式表示为：

现对这三种方法得到的联合移位因子进行比较，以30℃、13.3MPa 为参考条件，将34℃、16MPa 下的试验曲线向参考条件移位。⑴利用平移函数计算获得的联合移位因子为1.021。⑵先应力移位后温度移位：将34℃、16MPa下的蠕变柔量曲线先向34℃、13.3MPa的曲线平移，由表2 可知恒温应力移位因子为0.668，再向30℃、13.3MPa的曲线平移，由表1可知恒力温度移位因子为0.391，最终得到的联合移位因子为0.668+0.391=1.059；⑶先温度移位后应力移位：将34℃、16MPa 下的蠕变柔量曲线先向30℃、16MPa 的曲线平移，恒力温度移位因子为0.402，再向30℃、13.3MPa 的曲线平移，恒温应力移位因子为0.648，最终得到的联合移位因子0.402+0.648=1.05。

可以看出，通过三种方法获得的温度-应力联合移位因子间的相对误差较小，基本在10%以内，表明三种移位方法都具有合理性，同时也验证了联合移位因子分步获取的可行性。

4 结论

⑴温度和应力对PET 材料的蠕变性能具有明显的加速效果。温度越高，PET 的蠕变变形越大，应力越大，PET 的蠕变柔量增长速率越大。PET 在试验条件下表现出明显的非线性特征。

⑵通过温度移位因子和应力移位因子可以将不同温度和应力下的蠕变柔量曲线在对数时间坐标轴上移位得到参考条件下的蠕变柔量主曲线。将两条主曲线在同一坐标系上耦合，两者在对应时间尺度上重合度较好，20 条蠕变柔量曲线交汇形成的耦合柔量主曲线呈统一的变化规律，验证了时间-温度-应力等效原理在PET材料的适用性。

⑶利用温度-应力联合移位因子可以将任意条件下的力学曲线向参考条件移位。温度-应力联合移位因子可以直接计算得到，也可以由恒力温度移位因子和恒温应力移位因子分步获得。三种不同方法获取的温度-应力联合移位因子比较接近，误差在10%以内。