Benford与XGBoost模型融合的财务风险预警研究
——基于2000-2021年沪深A股上市公司数据分析
王 冲 刘亚丽
一、引言
公司的经营必然会与风险相伴,这让公司的未来充满了更多的不确定因素。如果公司没有控制好自己的风险,就会导致公司陷入财务危机。一般而言,公司倒闭危机初期总会出现一些局部问题。在财务方面,它会呈现为单个和与之有关的指标的异常,这就是所谓的财务风险预警。一个有效的财务风险预警系统,可以对企业运营管理进行预警,防止企业破产。企业的财务风险受多种因素的影响,而各种因素的作用最后又会通过财务指标反映到企业。所以,要对财务危机企业和正常企业在财务指标上存在的不同点进行分析,找到财务风险与财务指标之间的关系,构建出危机预警模型,这样能够使公司高管及时判断、预防及管控财务危机。
随着信息化进程的加快,财务风险的预测已由传统的统计学方法向更加智能、更加精确的人工智能方法发展。流行的基于机器学习(ML)的财务风险预警模型包括朴素贝叶斯(NB)、神经网络(NNS)、K-近邻(KNN)、支持向量机(SVM)、决策树(DT)等。集成学习算法是将多个弱分类器聚合为一个较强分类器,被认为是主流的基于ML 的模型(Pavlicko et al.,2021;Yan et al.,2020)。像梯度提升树模型(GBDT)(Liu et al.,2022)这样的增强集成方法被认为是财务风险预警的流行解决方案。
然而现有研究较少考虑财务数据质量的问题,最近几年国家一直在加强对上市公司的监督。但是财务舞弊仍然时有发生,迫切需要探索一种新的财务风险预警模式(钱苹和罗玫,2015)。财务舞弊指的是一家公司为了虚报利润,来美化价值表现,利用各种手段,刻意修改自己的财务指标数据,从而高估自己的资产或低估自己的负债(余思明等,2020)。会计造假会造成会计信息的扭曲,使会计信息质量下降,从而对会计信息的风险预警能力产生很大的影响。在构建财务风险预警模型的时候,一定要对财务数据质量问题所带来的影响进行充分的考量,从而提升对财务风险预警模型进行预测的精度(杨贵军等,2019)。
本文考虑到财务舞弊等原因对财务数据质量的影响,以我国A股上市公司2000-2021年的财务数据为研究样本,根据Benford 律构造Benford 因子,构建基于集成方法XGBoost的财务风险预警模型,本文的研究成果将为企业在危机发生前预警、防范风险、提升企业经营效率等提供参考。
二、财务风险预警研究进展
1930 年至今,针对企业财务风险预警的研究方法从开始的趋势分析、判别分析,再到现在的人工智能技术,从传统的计量模型再到机器学习模型和深度学习模型的应用,财务风险预警模型的研究日渐成熟,为企业财务风险预警研究奠定了基础。
对公司破产危机预警的研究,国外相对更早一些。1920 年起,针对财务比率的分析就已经在企业财务状况分析中占据重要地位,例如著名的杜邦分析法,通过几个重要财务指标之间的分解和联系,从而综合分析企业的财务状况。这是一种经典的财务业绩评价方法,一直被沿用至今。而学术界认可的最早的财务风险预警研究,即单变量分析,也是基于财务指标进行预测。单变量预警模型最早由Beaver(1966)所提出的,该模型是研究某个单一的财务指标的变化趋势,从而对公司未来的危机进行预警。他的研究选取了158 家企业作为样本量,并采用AB测试,即79家为危机企业,再找79家行业和规模与之相匹配的正常企业进行对比分析,选取了30个财务指标进行研究,时间窗口为1954-1964 年期间。研究表明正常企业和陷入财务危机的企业财务指标之间存在较大差异,通过单变量的差异分析对财务风险预警有一定作用。然而该模型的问题也很明显,仅通过单一变量去预测企业整体财务状况是不准确的。单变量预警模型随机性和抗干扰性较弱,容易受到外部因素的干扰而得出错误结论。于是,Ratios(1968)提出了基于Beaver单变量模型的改进模型多元变量模型,也就是著名的Z-Zscore 模型。该模型的核心是采用多元线性判别方法,用多个指标测试财务风险,然后通过赋权综合计量得出一个计量值Z 值。通过判断Z 值的大小来预测企业整体财务风险的可能性,该值越大发生危机的可能性越高,相反则越低。虽然该模型改进了单变量模型的不足之处,但实际应用中很难满足该模型苛刻的统计假设前提。
在国外学者提出将判别模型应用于财务风险预警研究并取得显著效果后,国内的学者通过借鉴国外的经验在该领域的研究也迅速发展起来。最早由吴世农和黄世忠(1987)将判别模型应用与国内企业财务风险预警,验证了该模型在国内企业同样适用。后来的陈静(1999)同样借鉴了国外的研究方法,选取国内ST 和非ST 配比公司各27 家做AB 测试对比实验,并分别进行单变量和多变量判别模型预测,研究验证了多元判别模型的预测准确性效果更好。随后的张玲(2000)在陈静的研究基础上,以A 股上市公司为研究样本进行实验,结果进一步验证了上述结论。周首华等(1996)在改进Z-score 模型基础上提出F-score 模型,与Z 计分模型相比,F-score加入了现金流量自变量,充分考虑了在财务危机预警中现金流量比率这一有效变量。
无论是单变量模型还是多元线性判别模型都存在其方法论的假设条件,如样本需满足高斯分布,且变量之间不存在多重共线性及配比样本均方差矩阵相等。为了提高模型的适用性和有效性,Martin(1977)选择了较低样本分布要求并且适用性更广的Logistic 回归模型,与线性回归模型相比,logistic 不要求样本数据服从正态分布以及相关严苛的前提条件,打破了传统线性判别方法难以实际应用的困境。Martin的研究表明,与传统线性判别模型相比,Logistic模型的财务风险预测效果更好。Ohlson(1980)截取1970-1976 年间105 家危机企业和2058 家非危机企业为研究对象,发现非财务指标,如企业规模、资本结构等也能预测财务风险。吴世农和卢贤义(2001)以国内企业为样本采用相同指标体系,进行多元判别模型和Logistic 模型预测财务风险对比实验,验证了logistic模型的预测精度更高。此后一些学者对Logistic回归预警模型的参数估计方法进行研究,如Jabeur(2017)应用偏最小二乘法对于精模型进行求解,并考虑了缺失数据的处理。
人工智能的发展加速了各个领域的研究发展,越来越多的学者倾向于将计算功能强大的人工智能技术引入财务风险预警研究。神经网络算法是人工智能技术的一个基础算法,源于模拟人脑神经的研究。相较于线性判别模型和logistic 这些传统数量统计计量模型,神经网络对样本要求较低,没有统计假设前提,适用性更强而且预测准确性高。Dutta(1988)在研究债权等级分类时最早引入神经网络进行研究。Odom(1990)在对财务风险预警研究中,将线性判别模型和神经网络做对比,发现神经网络模型的预测效果更好。我国最早关于神经网络财务风险预警的研究是1995年黄小原发表的文章,但也仅是理论阐述。王玉冬等(2018)分别对比了FOA和PSO这两种算法优化后的BP模型的预测效果,研究发现后者的性能更优。
除神经网络外,作为机器学习中备受欢迎的支持向量机(SVM)算法也被应用于财务风险预警研究。它是一种以统计理论为基础的ML 方法。该方法泛化能力强,在各种实际问题中表现优秀。Li et al.(2014)将SVM、Logistic 和Z 模型进行对比实验,结果显示SVM 的预测准确性更高。刘玉敏等(2017)构造了PCA-PSO-SVM 财务风险预警模型,先用PCA降维,再用粒子群算法对SVM进行优化,得到比单一SVM预测性能更好的优化模型。
随着人工智能技术渐渐成熟,研究者开始倾向于融合多个模型的集成学习算法,集成学习方法是将多个弱分类器整合起来构造一个强分类器,通过整合多个学习器,可以得到比单一分类器明显优越的泛化性能,目前被认为是基于ML 的主流研究方法。West et al.(2005)为了使单一分类器尽可能有较大的差异,于是采用bagging 提升方法构造企业风险预警模型,并和神经网络模型对比,实验证明了集成学习算法的优越性。同年谢纪刚等(2005)也采用bagging 方法,以国内上市企业为样本构造了国内企业财务危机预警模型。Choi et al.(2018)提出了一种基于集成分类器的承包商财务困境预测模型,将六个单分类器,如支持向量机(SVM)、人工神经网络(ANN)、逻辑回归(LR)、决策树(CART)、K 近邻(KNN)和朴素贝叶斯(NB)分别和综合这六个模型的集成分类器相比较,利用2007-2012 年韩国承包商的财务报表评估了模型的预测准确性,研究显示集成分类模型的预测性能比单一分类器的效果好。Wang et al.(2018)发现在以往的研究中,文本信息,情绪信息等非财务信息预测信息和阶层失衡问题往往被忽略,于是他们用CSMAR 数据库中的上市公司为研究样本,将情感和文本信息结合到集成随机子空间方法(ISTRS)中进行财务风险预警。结果表明,该方法能够显著提高财务困境预测性能。Xu et al.(2021)将定性分类器(专家系统法,ES)和定量分类器(卷积神经网络,CNN)相结合,并且引入互联网搜索指数作为财务困境预测的新变量,通过构建每个分类器的软集表示,然后利用软集上的最优决策来识别企业的财务状况,结果表明该模型的准确性和稳定性方面有较好的表现。Liu et al.(2021)提出了一种用于信用评分的多粒度多层梯度增强决策树(GBDT)。多层GBDT考虑了基于树的模型的显示学习过程和区分申请人好坏的表示学习能力的优势。在6个信用评分数据集上的实验结果表明,分层结构可以有效的减少信用评分数据集的类内距离,增加信用评分数据集的类间距离,从而进一步提高信用评分的性能。
国内外大量文献均已证实了机器学习人工智能对公司财务风险预警的良好表现,但少有关注财务数据质量对集成学习模型预测准确性影响的研究。现实中,为了避免持续亏损导致的“退市”,企业常常会产生“粉饰”的心理,随着企业的经营业绩不断恶化,企业对会计信息的控制也会不断增强。所以,在上市公司存在着财务数据操纵的情况下,财务风险预警研究应该将企业的财务数据质量作为重点,建立预警指标体系并建立预警模型时,应该将财务指标和数据质量结合起来。Benford定律是一种基于财务数据开头数字的分布规则,它可以用来检验财务指标数据的质量。如果一组数据的头位数字的观察频率与Benford 律不符合,则很大概率有人为操纵的嫌疑(Nigrini &Mittermaier,1997)。而Benford 定律可以有效地鉴别出各类财务信息的造假行为,并被广泛地应用于会计理论与实践中。赵莹等(2007)利用Benford 定律,对危机和正常两类公司的净利润特征第一个数值分布情况进行了检验,并得出了A股净利润的数值操作规则。罗琪(2020)也是用相同的方式,把Benford 因子加入到SVM中,最后得出的结论是,Benford因子可以帮助预测一家公司是否会出现财务危机,带有Benford因子的组合模型的预测效果更好。杨贵军等(2022)除了构造Benford 因子外,还根据Myer 指标构造了Myer 因子,带入到BP 模型进行预测,研究表明:两种因子都提高了BP 模型预测的精度。因此,本文用Benford 律来检验财务指标的有效性和真实性,构造Benford-XGBoost预警模型,一方面既发挥了XGBoost集成分类器的优势,又能保证用于预警的数据集的数据质量,从而保证预警模型的有效性。
三、Benford因子
(一)Benford定律
Benford 定律是指任何未经过人工刻意设计的自然数据,其第一个数字的排列分布具有一定的规律。即数字1 到9 的概率分布是单调递减的,Hill(1995)给出了Benford定律的数学公式。记d=1,2,3,...,9,首位数字D为d的概率为:
在一组数据中,统计每个样本的第一顺位数字出现频率,若满足上述公式,即表明数据的质量好。判断第一顺位数字分布律是否满足Benford律的一般方法为χ2拟合优度检验,公式如下:
公式(2)中N 为样本量、fd为d 的观测频率、fB,d为Benford定律。若χ2值超过10%显著的临界值,则否定原假设,并且财务数据第一位数字的频率被认为与Benford定律不一致。然而通过这种方法,只能总体评判出该组数据质量的好坏,但并不能定位到某个具体样本点。因此,本文参考杨贵军等(2022)的研究,构造Benford因子带入XGBoost模型。
(二)数据质量因子的构造方法
假设X(ii=1,2,3,...n)为不符合Benford定律有质量问题的变量数据,记Xi第一位数字d的观测频率fd与Benford定律的理论频率fB,d的差值为。
依据Benford定律的显著性检验原理,指标Xi(i=1,2,3,...n)的某个首位数字观测频率不同于理论频率极有可能存在舞弊操作,并且这种操作往往会存在某种倾向,实际表现为首位数字的观测频率会远大于理论频率。因此,本文将首位数字中观测频率高于理论频率的最大数字视为风险值。记差值最大且为正数的首位数字为ui,差值最小且为负数的首位数字为ni,有如下公式:
考虑到差值的正负,有两种指标Xi(i=1,2,3,...n)的Benford 质量因子构造方式。记为Ci s和Cs,如公式(6)和(7)所示:
公式(6)和(7)中,若观测样本点S的指标Xi,s的首位数字满足ui,则取值1,否则取值0,Cs同理。
(三)基于Benford定律的XGBoost模型
在已收集的数据集E={(X1,Y1),(X2,Y2),...,(Xn,Yn)}(其中Xi=(Xi,1,Xi,2,...Xi,k)表示自变量,Yi表示分类变量,n 为样本量,k 为指标个数)的基础上,利用Benford 定律理论对数据集E 进行数据质量检验并构造Benford因子。根据公式(6)和(7)将构造好的Benford 因子与数据集E 整合,再带入模型进行实验。
四、模型构建方法
(一)模型构建流程
本实验选取XGBoost 算法进行财务风险预警建模。整个基于XGBoost 的A 股上市公司财务风险预警及其特征分析模型的构建流程如图1所示,主要包括因子构造、模型训练、超参数优化、多模型对比以及模型解释分析等核心模块。
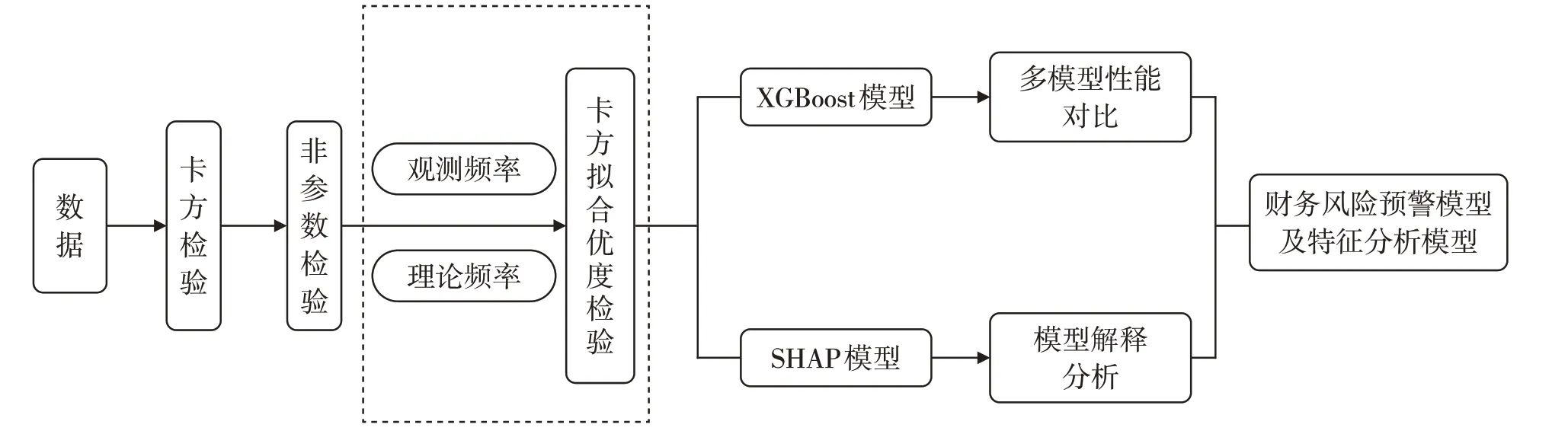
图1 财务风险预警及特征分析模型流程图
(二)XGBoost模型
XGBoost 是一种新型的梯度增强算法,由于其高效的并行训练和基于ML应用的显著改进,在ML应用的比赛中很受欢迎。XGBoost是集成方法GBDT的变体,它结合了梯度增强优化策略和DT分类器,即将多个DT组合成一个梯度提升框架,迭代优化训练目标。GBDT是由m个基学习器加成组合模型,若第m 次迭代训练的树模型为fm(xi),则GBDT的表达式为:
其中,L(m)表示的是真实值yi与其预测值之间的差值。为了缓解过拟合问题,XGBoost 在损失函数中增加了正则化项∑kΩ(fm),结合上述两个公式,可以得到如下的XGBoost损失函数:
然后对上述公式进行二阶泰勒展开,去除常数项,公式推导如下:
其中,gi、hi分别表示目标函数的一阶导数和二阶导数:
而正则化项Ω(fm)用来衡量树的复杂度,分别由叶子结点数量和叶子结点权重两部分组成。展开式中,T代表叶子结点的个数、w表示叶子结点的权重,为防止过拟合通过系数γ 和λ 进行控制。正则化项表达式如下:
定义一棵树fm(x)=wq(x),w∈RT,q:Rt→{1,2,...,T},包括两部分:叶子结点的权重向量w 和叶子结点的映射关系q。将fm(x)和正则化项展开式带入(13)式:
五、中国A股上市公司财务风险预警分析
(一)财务风险预警指标体系
现有财务风险预警研究大都是用财务指标数据,本文参考现有研究,分别从偿债能力、盈利能力、发展能力、营运能力和现金流量这五个方面选取财务指标进行模型训练,如表1所示。

表1 财务风险预警指标
(二)样本选取与数据来源
本文参考现有文献,选取2000-2021 年A 股上市公司中标记为ST 的公司为研究对象,并选择被标记为ST 的上一年的财务数据作为实验数据,然后在相同年份同一行业中按照资产规模相近原则匹配正常公司,即未被标记为ST 的上市公司。实验数据剔除了金融业的上市企业。经过缺失值处理后,各得到174家上市公司。将列为ST的上市公司标记为1,未列为ST的公司标记为0,并作为模型的预测变量。以上数据来源于CSMAR数据库。
(三)指标变量的筛选
在进行Benford 因子构造前,先对财务指标特征进行差异性检验,通过差异性检验对指标进行初选,可以过滤掉一些对预警模型无效的指标。本文采用SPSS23.0 先对各项指标进行K-S 正太分布检验,若不满足正太性,则采用非参数Wilcoxon检验。结果如表2所示:
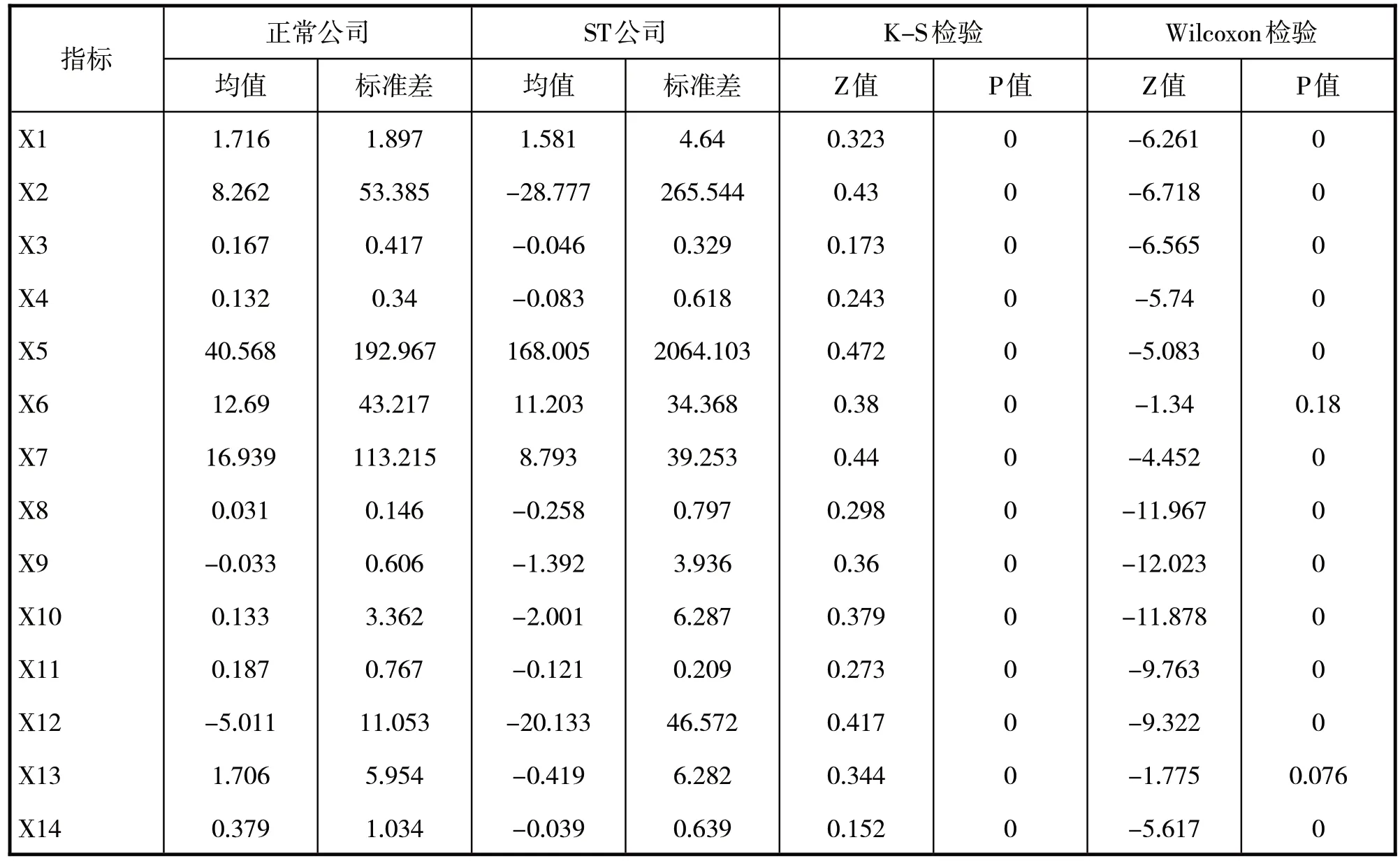
表2 ST公司与正常公司财务指标的差异性检验
由表2 中的K-S 检验结果可以看出,p 值均显著,表明拒绝原假设,14 个特征均不满足正太分布。因此用非参数Wilcoxon 对上述14个特征进行差异性检验,从表2的p值可以看出,在本文选取的14 个财务指标中,除存货周转率(X6)和每股经营活动产生的净流量增长率(X13)的非参数检验不显著外,其余12 个财务指标都可以显著地区分ST公司和正常公司。因此删掉存货周转率(X6)和每股经营活动产生的净流量增长率(X13),用剩余的12个指标构造Benford因子带入模型。
(四)构造Benford因子
表3 是筛选出的12 个指标的观测频率和理论频率的卡方拟合优度检验结果,显著性水平10%的检验临界值是20.09。当χ2值大于20.09 时,则表明该指标存在质量问题。
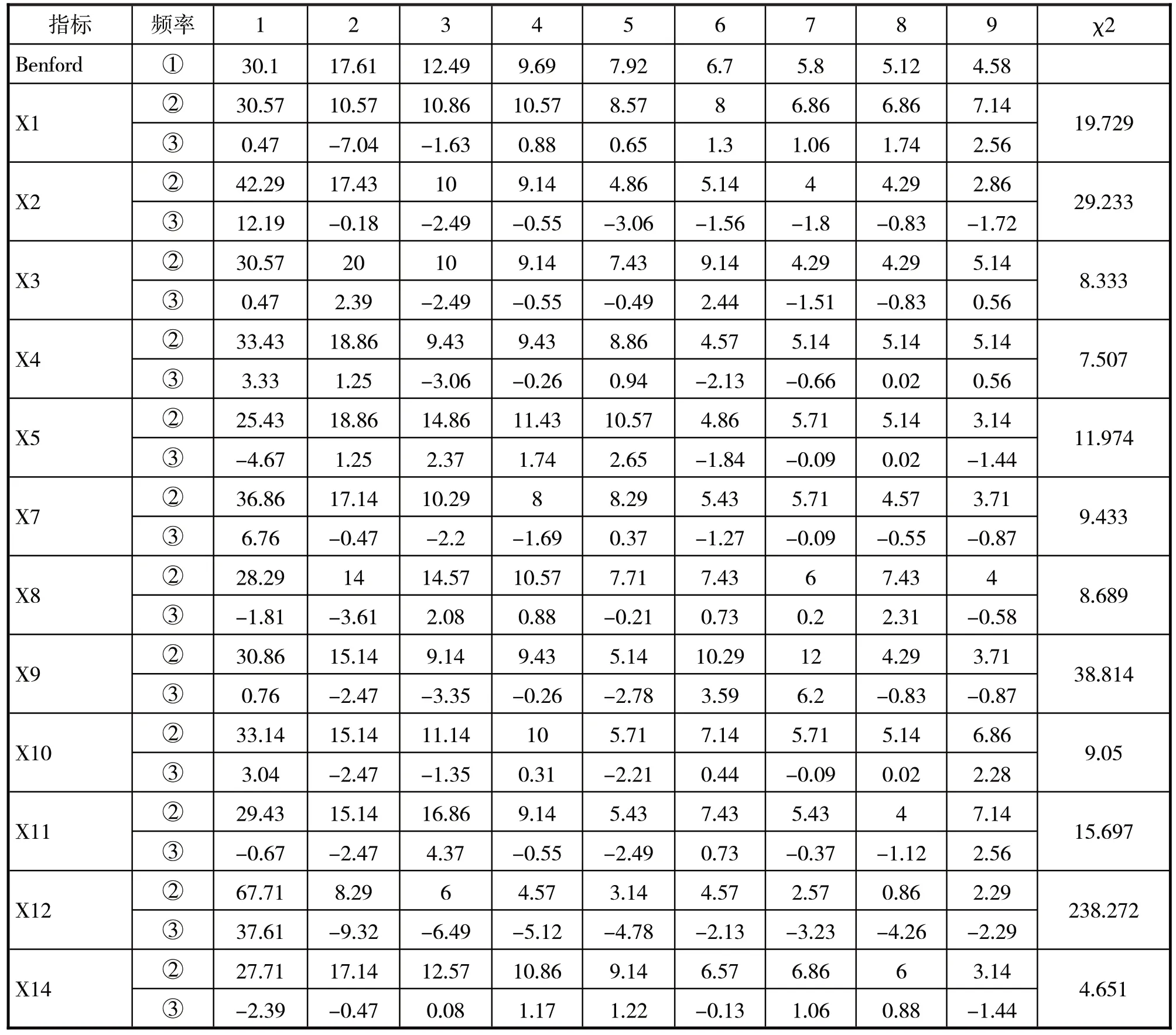
表3 财务指标首位数字观测频率与卡方拟合优度检验结果
从表3 中的χ2检验的结果可以看到,利息保障倍数(X2)、净资产收益率(X9)和营业利润增长率(X12)的χ2都超过了临界值,说明这三个指标的首位数字分布频率不满足Benford 定律,观察指标X2、X9、X12 的首位数字,可以发现其与Benford 理论频率正向差值最大的数字分别是1、7、1,根据公式(6)构造相应的因子并标记为B1、B2、B3。X2、X9和X12的首位数字中与Benford理论频率负向差值最大的数字分别是5、3、2,根据公式(7)构造相应的Benford质量因子,记为B4、B5、B6。将构造好的这6个因子以及上述12个财务指标带入XGBoost模型进行训练。
(五)构建基于Benford定律的XGBoost模型
将上述构造的因子和原来的12个财务指标全部带入XGBoost模型。根据交叉验证思想,将数据集划分为训练集和测试集,其中训练集占80%、测试集占20%。通过训练集建立基于Benford 定律XGBoost 的初始模型,用测试集的预测准确率判断模型的优劣。利用中国A 股上市公司财务数据建立的基于Benford定律XGBoost模型的预测准确率。结合学习曲线对加入Benford因子和未加因子的模型进行最优参对比,图2和图3是加入Benford因子的XGBoost 财务风险预警模型和未加因子的预警模型,在不同n_estimators 参数下的交叉验证准确率的学习曲线,可以看到加入Benford 因子和未加因子的模型在n_estimators参数200左右时,两个模型的预测准确率都比较高。并且,由图2 和图3 可以看出,加入Benford 因子的模型在参数25-200 范围内的整体交叉验证准确率均高于未加因子的模型。

图2 加入Benford因子的不同n_estimators下交叉验证准确率
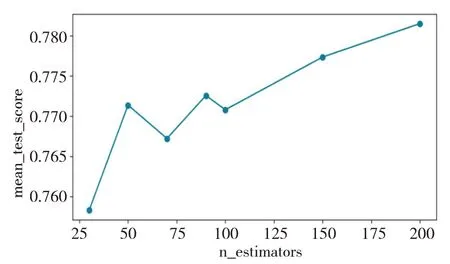
图3 未加因子的不同n_estimators下交叉验证准确率
为进一步说明加入Benford 因子的XGBoost 模型的预测效果,计算模型的准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值。其中准确率(Accuracy)作为最基本的一个评价指标,是指将实际非ST公司分类为正常公司或将实际ST公司分类为ST 的比例。精确率(Precision)是指实际ST 公司样本中被分类为ST样本的比例。召回率是指分类正确的ST公司样本占整个数据集中所有实际ST公司个数的比例。分类矩阵见表4,计算公式如下:

表4 分类结果混淆矩阵
将加入Benford 因子和未加因子的XGBoost 模型的预测效果进行对比,实验结果如表5 所示,可以看到,加入Benford 因子的XGBoost 模型的准确率、精确率、召回率和F1值都高于未加因子的XGBoost 模型。且加入Benford 因子的预测准确率比原有模型的预测准确率提升了3%。

表5 加入Benford因子和未加因子的XGBoost模型的预测效果对比
为使建模更具有说服力,将上述模型的建模过程分别重复100 次、200 次、500 次和1000 次,分别计算含有Benford 因子的XGBoost 财务风险预警模型和不含因子的XGBoost 模型的AUC、准确率、精确率、召回率、F1值,得到表6。可以看到不同迭代次数下,含因子的模型整体预测效果优于不含因子模型的预测效果。
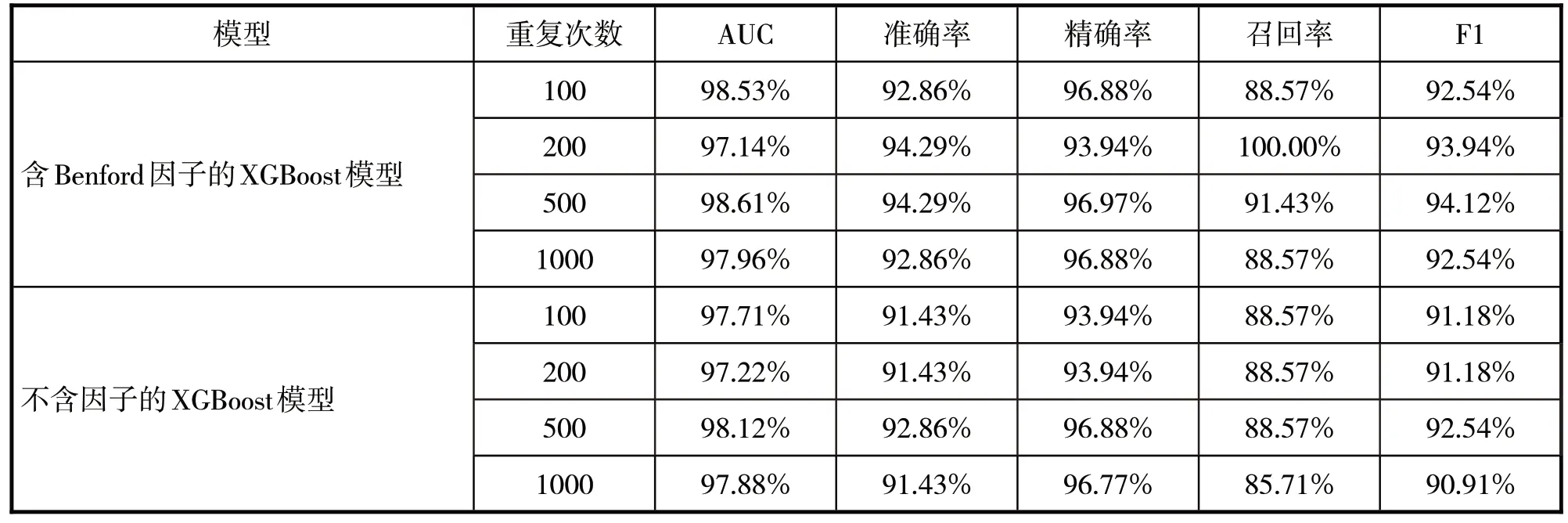
表6 加入Benford因子和不加因子的XGBoost模型预测效果对比
(六)与已有工作的实验对比
将XGBoost模型与已有的基于逻辑回归(LR)、KNN、极端森林(DF)、决策树(DT)以及GBDT 几种模型进行对比实验,结果见表7 和图4。从表中可以看出,与其他模型相比,XGBoost 模型的预测性明显优于其他模型。
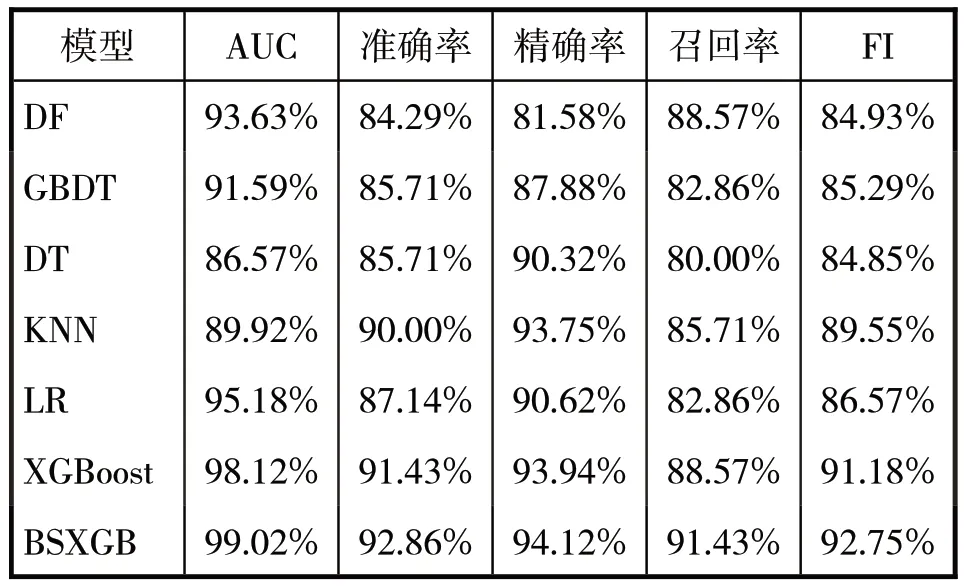
表7 模型性能对比
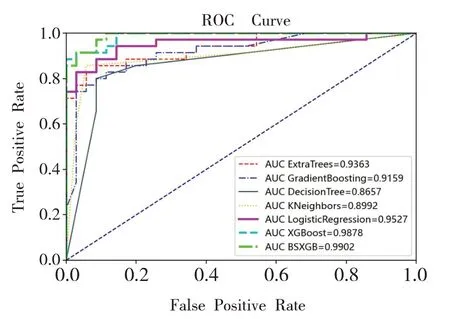
图4 多模型性能对比
(七)模型参数优化
通过上述实验结果,我们可以得出结论:XGBoost 模型具有较好的预测性能。为了进一步提高XGBoost模型的预测性能,本文对模型进行了参数调优。常用的超参数调参方法包括网格搜索、随机搜索和贝叶斯优化。其中,网格搜索是应用最广泛的超参数搜索算法,相当于穷举法且计算资源消耗较大。随机搜索则是从指定的分布中采样固定数量的参数设置,它一般比网格搜索要快一些,但结果不确定。贝叶斯调参是一种使用贝叶斯定理指导搜索以找到目标函数的最小值或最大值的方法,它会在进行一次迭代的时候,回顾之前的迭代结果,避免搜索那些结果太差的参数值,从而大大提高搜索效率。因此,本文选择贝叶斯调参方法来优化XGBoost 模型,进一步提高其预测性能。通过调参找到参数最优值,其中learning_rate 的最优值为0.3、max_depth 最优值为7、n_estimators 最优值为79,此时模型的预测效果达到最优,准确率达到92.86%,AUC值达到99.02%,相比未经过调参的XGBoost模型的准确率提高了1.43%,AUC 值提高了1.1%。
六、XGBoost模型指标贡献度分析
虽然XGBoost 算法的预测性能很好,但是和大多数机器学习方法一样存在可解释性差的问题,如同一个“黑盒子”无法衡量每个指标的贡献。因此,本文通过引入SHAP 模型计算出每个财务风险影响因子的shap value 值,以增强模型的可解释性。SHAP的全称是SHapley Additive exPlanation,这是一种可以用来解释较复杂的机器学习模型的后验推理方法。通常情况下,机器学习模型都是一个黑箱,只要在前端输入用于预警的指标,通过模型训练后就可以直接得出预测结果。然而,对于模型内部是怎样进行预测的,以及每个输入的特征在模型预测中发挥了多大的作用,我们并不清楚,尤其是一些较为成熟的集成学习模型,其解释能力更低,而SHAP模型则能很好的解决这一难题。SHAP以合作博弈论理论为基础,其关键在于对模型中的各个指标计算Shapley Value。SHAP将每个变量都当作“贡献者”,而且还可以计算出单个样本的预测值以及单个样本中各个变量的贡献值。
设第n 个样本为xn,样本xn的 第m 个特征 为xnm,模型对该样本的预测值为yn,整个模型的基线为ybase,则Shapley Value满足下列公式:
其中f(xnm)为xnm的SHAP 值,即为第n 个样本中第m个指标对最终预测值yn的贡献值,当f(xnm)>0,表示该指标有积极作用,可以提高预测值。若f(xnm)<0,则表示会降低预测值。
(一)全局归因分析
图5向我们展示了每个特征的Shap影响,每行代表一个特征,而每个点则代表一个样本。通过观察图5,我们可以清晰地了解每个特征对模型预测结果的影响程度,进而在优化模型的过程中有针对性地对特征进行调整。同时,图6则展示了各特征Shap值绝对值的均值,以此反映了每个特征的重要性。根据表中的数据,我们可以发现在XGBoost模型中,净资产收益率(X9)、营业利润率(X10)、资产报酬率(X8)、应收账款周转率(X5)以及经营活动产生的现金流量净额÷负债合计(X3)这五项特征,对于预测企业的财务风险预警模型具有重要的贡献。这些特征反映了企业的盈利能力、营运能力以及偿债能力,是影响企业财务风险的重要因素。此外,Benford 因子B2、B3、B4 在模型中也扮演了预测贡献的角色。这些结果为我们提供了更深入的洞察和优化模型的依据,进一步帮助我们理解模型预测结果的形成过程,提高模型预测的准确性和稳定性。

图6 XGBoost模型特征SHAP全局均值
(二)局部归因分析
SHAP方法是一种具有局部精确性质的特征重要性评估方法。它可以在单个样本上取得每个指标对当前模型预测结果的影响,这对于理解模型的预测结果非常有帮助。以测试集中的山东东方海洋样本为例,我们使用XGBoost模型对其当年的财务风险特征值进行预测,并使用SHAP图进行可视化解释。如图7所示,山东东方海洋2018年的最终值为5.34。我们发现净资产收益率(X9)、固定资产周转率(X7)、资产报酬率(X8)、应收账款周转率(X5)、经营活动产生的现金流量净额÷负债合计(X3)和利息保障倍数(X2)等特征值均为负数,并且表现为负数的特征值所占长度越长,预测结果为存在财务风险的概率越高。这些特征变量的影响可以通过SHAP图直观地展示出来,帮助我们更好地理解模型的预测结果。

图7 山东东方海洋2018年XGBoost模型SHAP图
七、结论
鉴于上市公司财务数据质量会对危机预警模型的预测效果产生偏差,本文根据Benford 定律构造了Benford 因子带入XGBoost 模型,通过带有Benford 因子的XGBoost 模型和未加Benford 因子的XGBoost 模型的预测精度、准确率等各项指标进行比较,实证检验结果表明,数据质量会影响财务危机预警模型的预测效果,并且通过Benford 因子还可以定位到那个样本点存在财务高风险。根据上述实验结论,本文还将带有Benford 因子的数据集用其他模型进行实验,对比逻辑回归(LR)、K-近邻(KNN)、极端森林(DF)、决策树(DT)、GBDT 几种模型和XGBoost模型的预测效果,结果表明XGBoost 模型的预测性能最好。基于机器学习模型的可解释性较差,本文引入了SHAP 模型对XGBoost 模型的特征贡献度进行分析,可以从全局进行归因分析,也可以从具体样本点进行归因分析,通过计算SHAP 值对模型中财务风险的影响因素进行解释分析,增强了模型的可解释性。

