船舶应急抛锚贯入深度计算方法研究

黄勇

摘 要：本文应用常规公式和有限元CEL大变形分析法，研究了3.5万吨级船舶7.09 t船锚、20万吨级船舶13.35 t船锚、40万吨级船舶18.8 t船锚在长江电力隧道工程锚地、航道等区域的应急抛锚贯入深度情况。常规公式法计算的最大应急抛锚贯入深度为4.37 m，CEL大变形分析法计算的最大应急抛锚贯入深度为5.33 m，常规公式无法考虑贯入过程中土壤的竖向和横向推力的变化，计算结果相对偏小，CEL大变形法则能考虑多层土壤刚度以及土壤刚度随土层变形增加后的折减，计算精度相对较高。针对地层组成多变的复杂情况，建议采用计算过程客观、精度高的有限元 CEL方法。

关键词：贯入深度；电力隧道；埋深

0 前 言

目前，输电线路工程在穿越长江等高等级航道时多采用电力隧道的形式，电力隧道的埋深直接影响工程安全和建设运行成本，如：电力隧道埋设过深会增加工程投资运行成本，埋设过浅会增加工程安全隐患。由于高等级航道上通航船舶等级较高，船舶流量密度较大，通航环境较复杂，存在通航船舶遇险后应急抛锚的情况，船舶应急抛锚贯入深度是影响隧道埋深的一个重要因素，如何合理准确的确定船舶应急抛锚贯入深度是一个难点，分析计算船舶应急抛锚情况下船锚贯入河床的深度，可为电力隧道工程的设计和敷设提供科学合理的依据。

本文根据工程河段航道条件、地质条件、水文条件等因素，确定了工程水域代表船型、锚型和锚重，对工程河段的水道、锚地、航道等区域开展应急抛锚贯入深度的分析与模拟计算，对比常规公式和有限元CEL大变形分析法计算的优缺点，为电力隧道工程的安全敷设提供了必要的设计参数，同时可为类似穿江隧道工程中船舶应急抛锚贯入深度计算提供参考。

1 应急抛锚贯入深度计算方法

1.1常规公式法

目前，常用的船舶抛锚贯入深度计算方法主要有经验预测模型法、Young公式法。

（1）经验预测模型法

经验预测模型法是根据不同种类船锚的抛锚贯入深度经验公式建模，并以此预测不同种类船锚的抛锚贯入深度。以船舶常用的霍尔锚为例，其抛锚贯入深度的经验公式为：

式中：d为抛锚贯入深度，α为锚爪展开角度，Ha为锚爪高度，为锚身厚度B1为锚身厚度。上述霍尔锚的相关结构参数可参考标准《霍尔锚》（GB／T546—2016）[1]。

虽然经验预测模型法实际运用较为简单，但其只考虑了锚自身尺寸的问题，而并未考虑河床底质特性，故很难以此确定船舶应急抛锚富余埋深。

（2） Young法

桑迪亚国家实验室从1960年开始研究土侵彻项目，至今已进行约3 000次试验，建立有重要的试验数据库。1997年，Young 的报告《侵彻公式》[2]在已有试验的基础上提出对土、岩石和混凝土使用形式相同但系数不同的公式，给出的物体贯穿土壤深度经验计算公式（Young公式）如下：

当V约 ＜61m/s时

当V约≥1m/s时

式（2）和（3）中：D为贯穿深度，m；N为物体的形状系数，一般平均值为9.61；S为土壤系数；W为物体的质量，kg；V为物体接触土壤时的速度，m/s；A为物体的横截面面积，m2。极端抛锚情况下，锚触底的贯穿情形适用于式（2）的形式。

1.2 CEL大变形分析法

在有限元分析中，主要通过有限元网格描述有关物理量。拉格朗日算法能够清晰地描述物体界面，但当所描述的物体发生大变形时，由于有限元网格的运动与物体质点的运动重合而使网格严重扭曲，将严重影响计算的收敛性；而欧拉算法中有限元网格在空间上固定不动，因此不会出现网格大变形问题，但是它很难给出精确的物体界面。耦合拉格朗日欧拉算法（Coupled Eulerian-Lagrange，CEL）是结合单纯的拉格朗日算法和单纯的欧拉算法各自的优点而得到的一种新算法，其采用拉格朗日网格离散结构物，采用欧拉网格离散河底土壤，结构物与河底土壤间的接触面采用拉格朗日域边界来描述，很好地解决了物体界面描述与网格大变形问题[3]。

2 基于工程实例的应急抛锚贯入深度分析计算及对比研究

2.1 工程概况

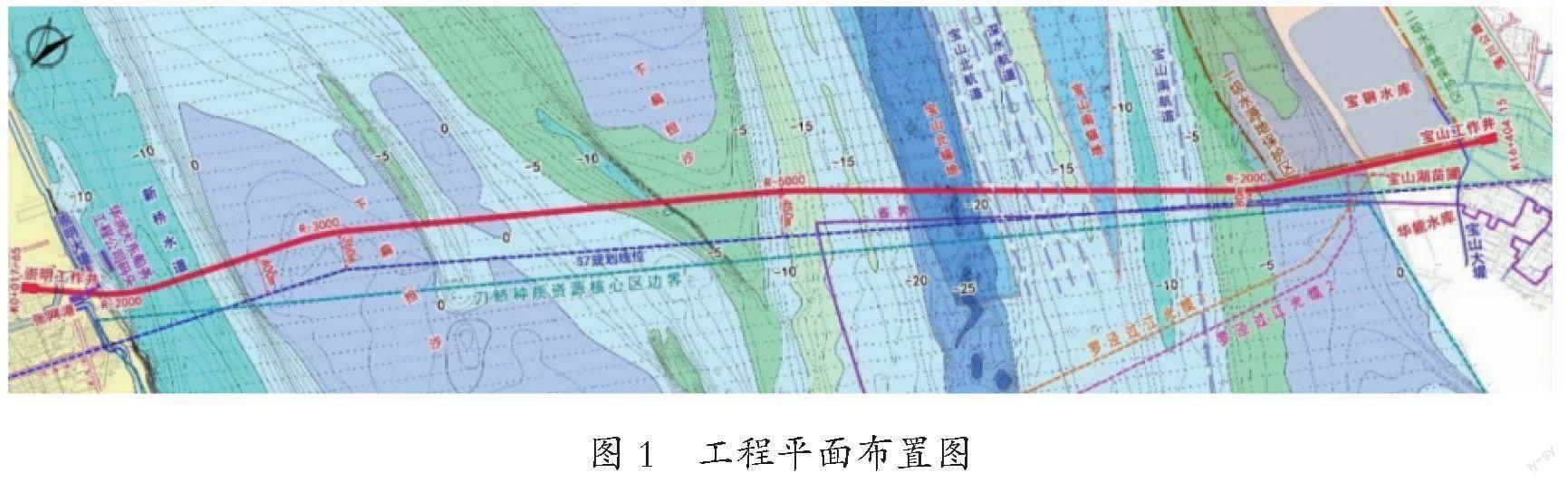
拟建电力隧道工程起自上海市崇明区城桥镇张网港东侧，沿宝钢水库西侧走行，至宝山罗泾镇新陆村登陆，工程全长约 16.4 km。本工程江中自东向西分别下穿长江南北主江堤、新桥水道、下扁担沙沙体、宝山北锚地、宝山北航道（含深水航道延伸段）、宝山南锚地和宝山南航道。工程平面布置图如图1所示。

拟建隧道工程穿越长江南支航道，通航船舶等级较高，船舶流量密度较大，通航环境较复杂，存在通航船舶遇险后应急抛锚的情况。

2.2 代表船型和錨型

根据工程河段船舶交通流、航道通航代表船型和锚地锚泊代表船型综合确定了应急抛锚计算代表船型和校核船型，根据工程河段调研和相关锚重计算方法确定了锚型和锚重。选取计算代表船型为3.5万吨级和20万吨级船舶，锚重分别为7.09 t和13.35 t，计算校核船型为40万吨级船舶，锚重为18.8 t，锚型均为AC-14大抓力锚。

2.3 公式法计算成果

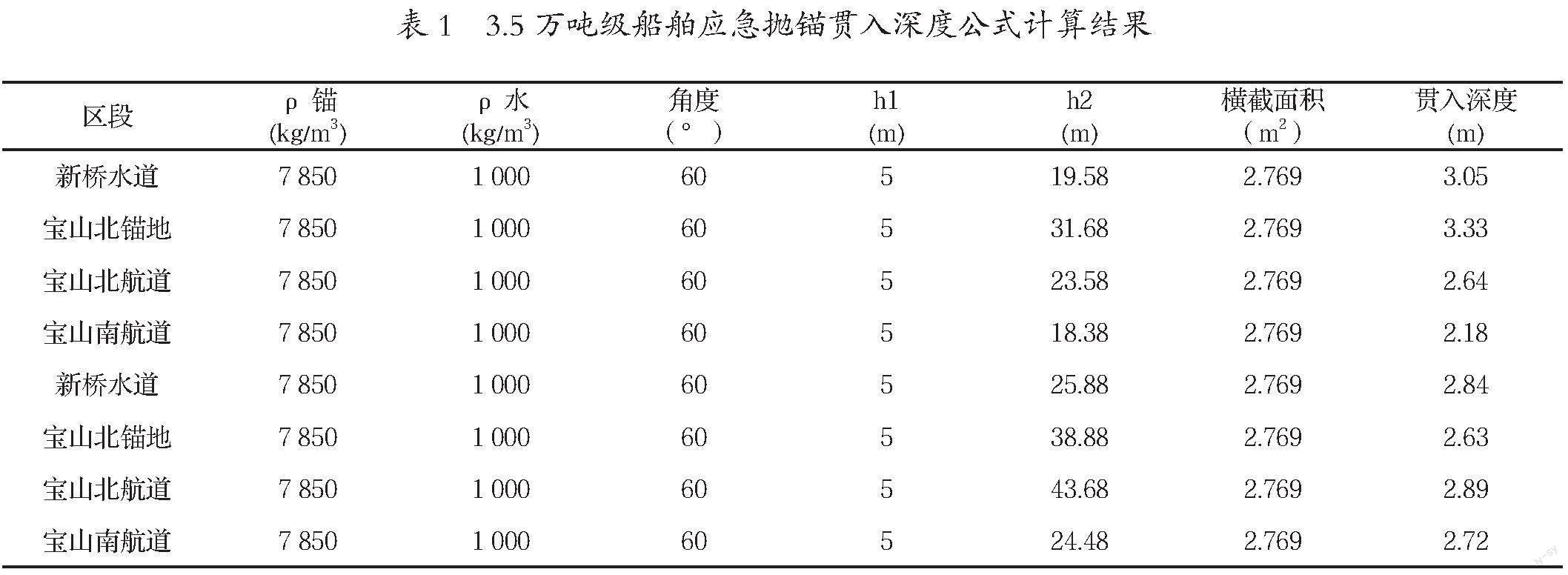
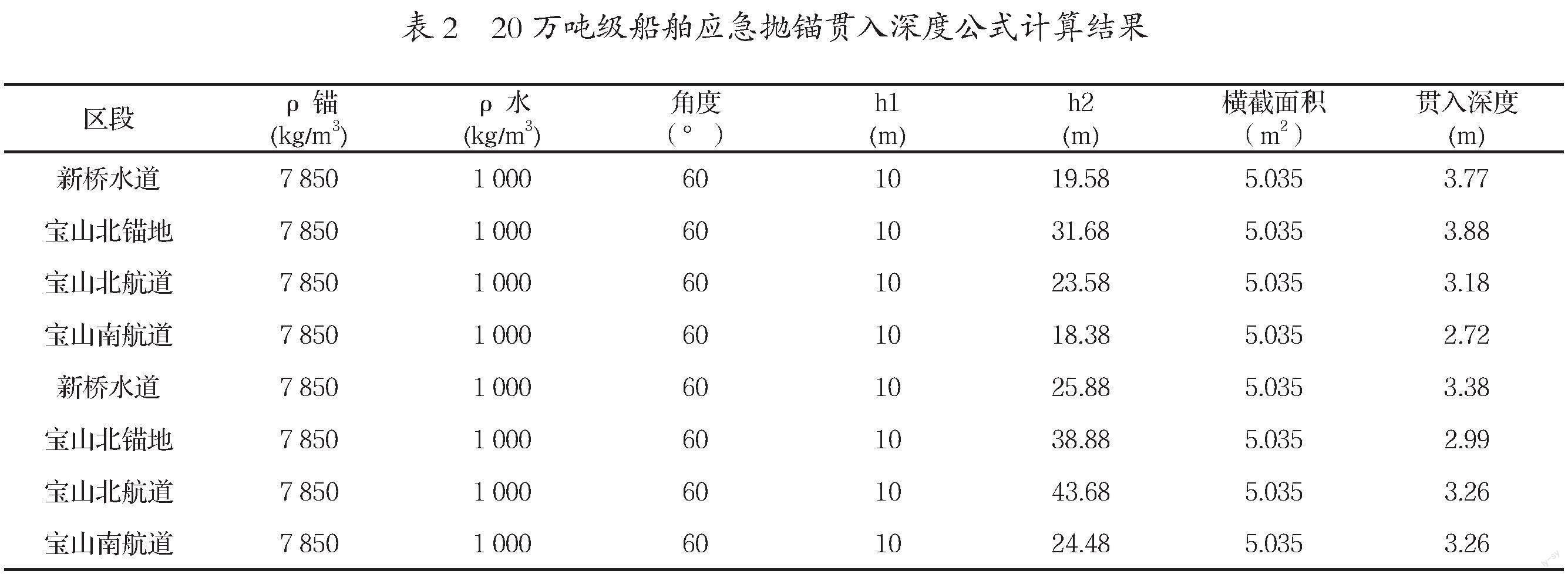
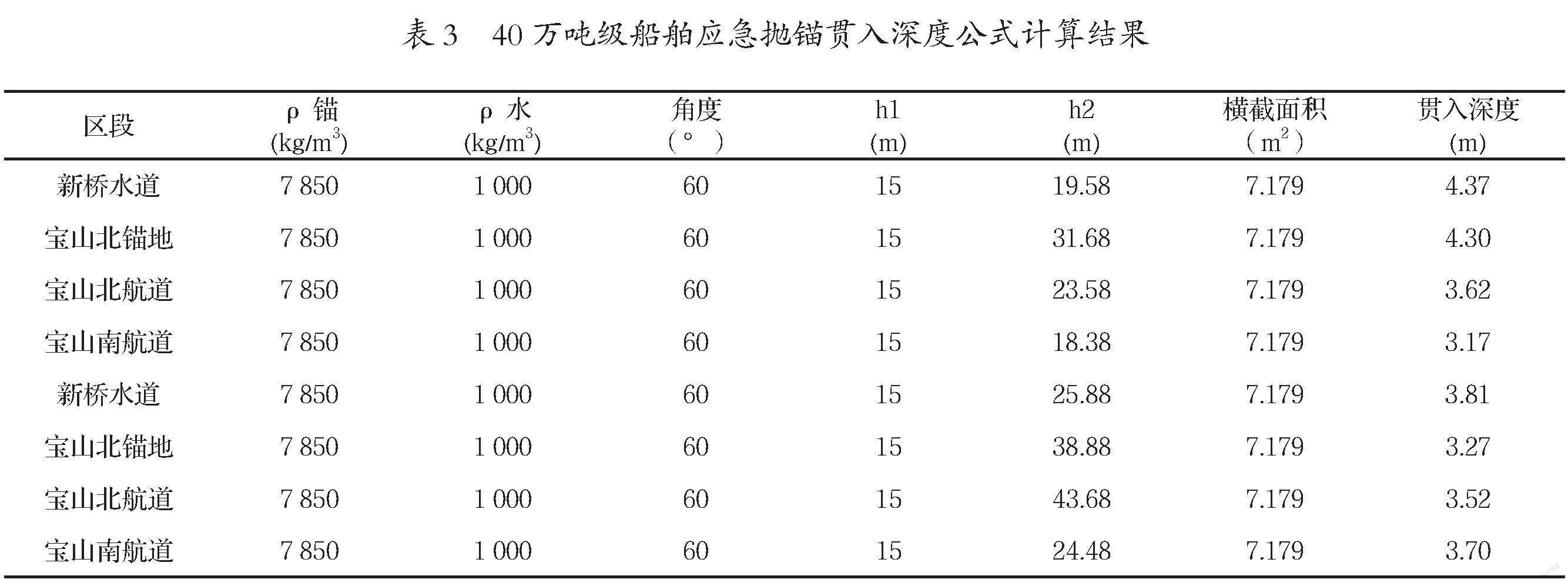
基于Young公式计算得到了隧道工程区域现状河床船舶应急抛锚贯入深度见表1—表3。

通过常规理论计算公式的分析可以发现，现状河床隧道工程区域3.5万吨级代表船舶应急抛锚最大贯入深度约3.33 m，20万吨级代表船舶最大贯入深度约3.88 m，40万吨级校核船舶最大贯入深度约4.37 m。

公式法计算成果受不变土壤系数、横截面积等因素的限制，首先在发生贯入时土壤的竖向推力和横向推力均在发生变化，始终不变将使结果偏小，不能反映最不利工况计算；第二是横截面积不变，实际情况中，不同角度的贯入，不同接触面积的贯入均会产生不同的深度。因此，采用常规的理论计算公式还存在不足之处，下面将采用有限元CEL大变形计算方法对应急抛锚贯入深度进行模拟，其中将充分考虑以上两方面的因素。

2.4  CEL大变形分析法计算成果

（1）几何模型

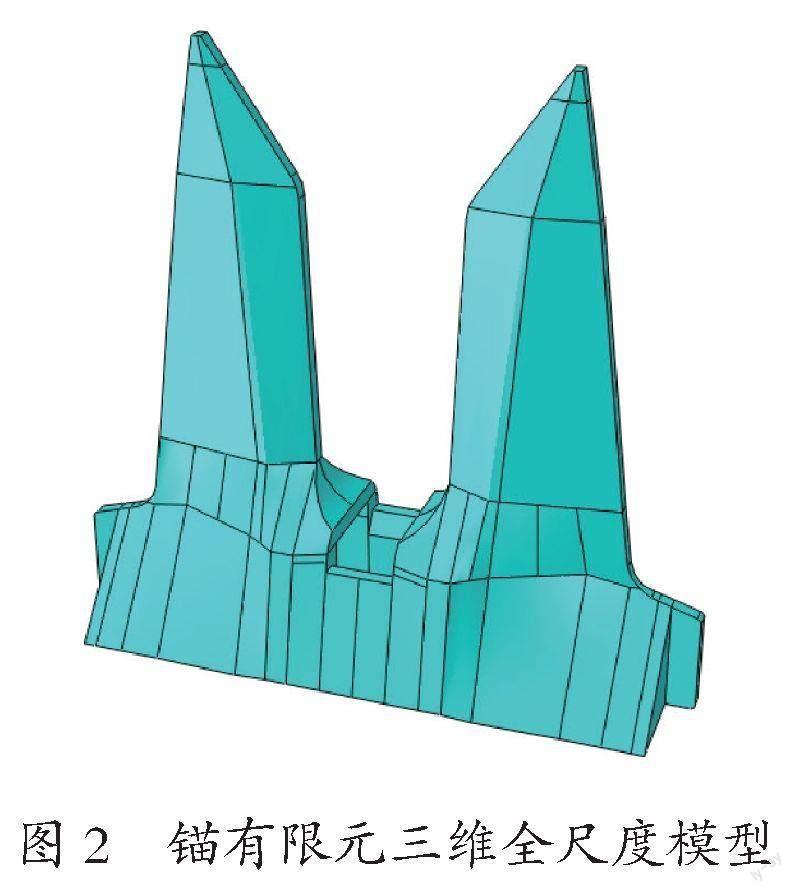
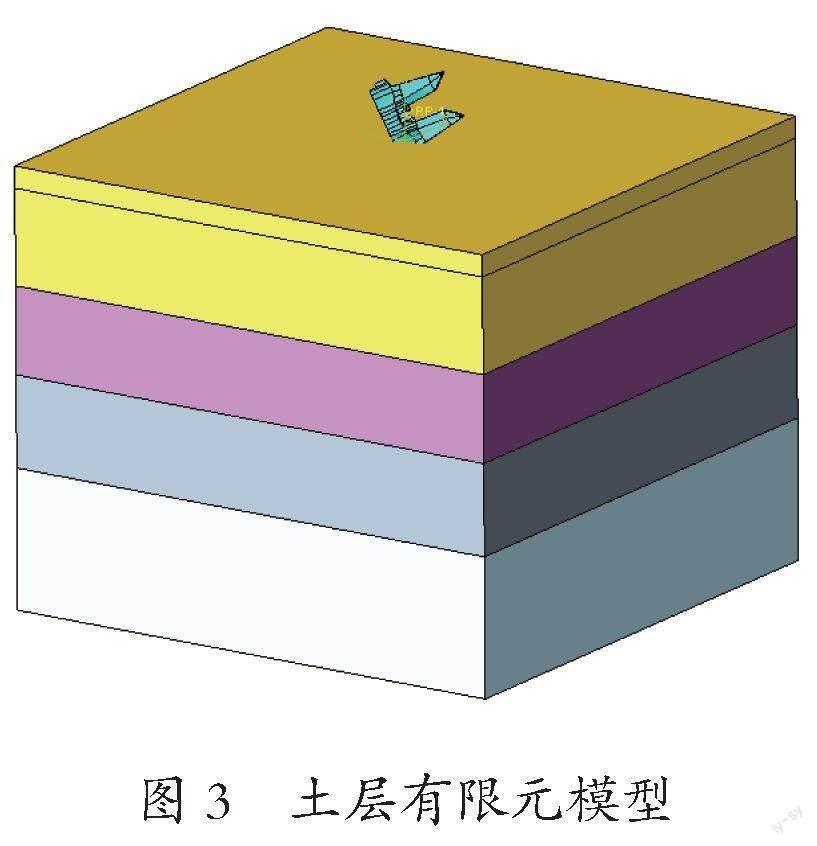
根据确定的锚的类型、尺寸和重量，建立了锚的有限元三维全尺度模型，如图2所示，并结合河床地层的组成建立了土层的有限元三维全尺度模型，范围为10 m×10 m（长×宽），深度按地层组成，抛锚区段的土层三维模型，如图3所示，其余区段的模型类似建模，此处不再一一列出。

（2）材料本构模型及边界条件

选取Mohr-Coulomb模型作为土层的本构模型。本项目中由于河床刚度和锚的刚度相差较大，因此计算时不考虑锚的变形，将其设定为刚体。土層欧拉体取10 m×10 m（长×宽），深度按实际地勘的土层厚度，侧部自由面约束相应法线方向的速度为0，底部约束竖向速度为0。土层欧拉体和船锚拉格朗日体之间采用接触算法，即法相正压力，切向摩擦力，正压力根据土层力学性质时得到，摩擦系数取0.25。

（3）地应力平衡

地应力是存在于底层中的未受工程扰动的天然应力，也称岩体的初始应力、绝对应力或原岩应力，广义上也指地球体内的应力，在该应力的作用下，岩体仍然保持零位移的状态，若不考虑地应力，直接给岩体施加重力，岩体将产生较大位移量，并伴随着大的应力状态，这与岩体的初始状态不符，因此在模拟时必须使模型首先达到地应力平衡。

（4）网格及求解方法

在船舶抛锚有限元模型建立过程中，采用八节点欧拉单元EC3D8R 模拟土壤，采用八节点拉格朗日单元C3D8R模拟锚，并将其定义为约束于参考点的刚体。其中模拟土层的EC3D8R欧拉单元数为272 484个，模拟锚的C3D4拉格朗日单元个数为183 552个。采用三维单元模拟土壤，分别选取对应于8倍锚爪宽度与厚度及8倍锚杆高度的范围作为计算区域，以减小边界效应对计算结果的影响。同时对落锚区域土壤网格进行局部加密。

（5）船锚触底贯入姿态

有限元CEL方法中加入了正向、侧向和斜向贯入的工况，充分验证了接触面积对贯入深度的影响。在应急抛锚时，由于船锚将受到水浮力的影响，其接触河床时的姿态无法判别，正向、侧向和斜向贯入的可能性均存在，因此找出其在各种姿态下的最大贯入深度是有必要的。

（6）计算成果

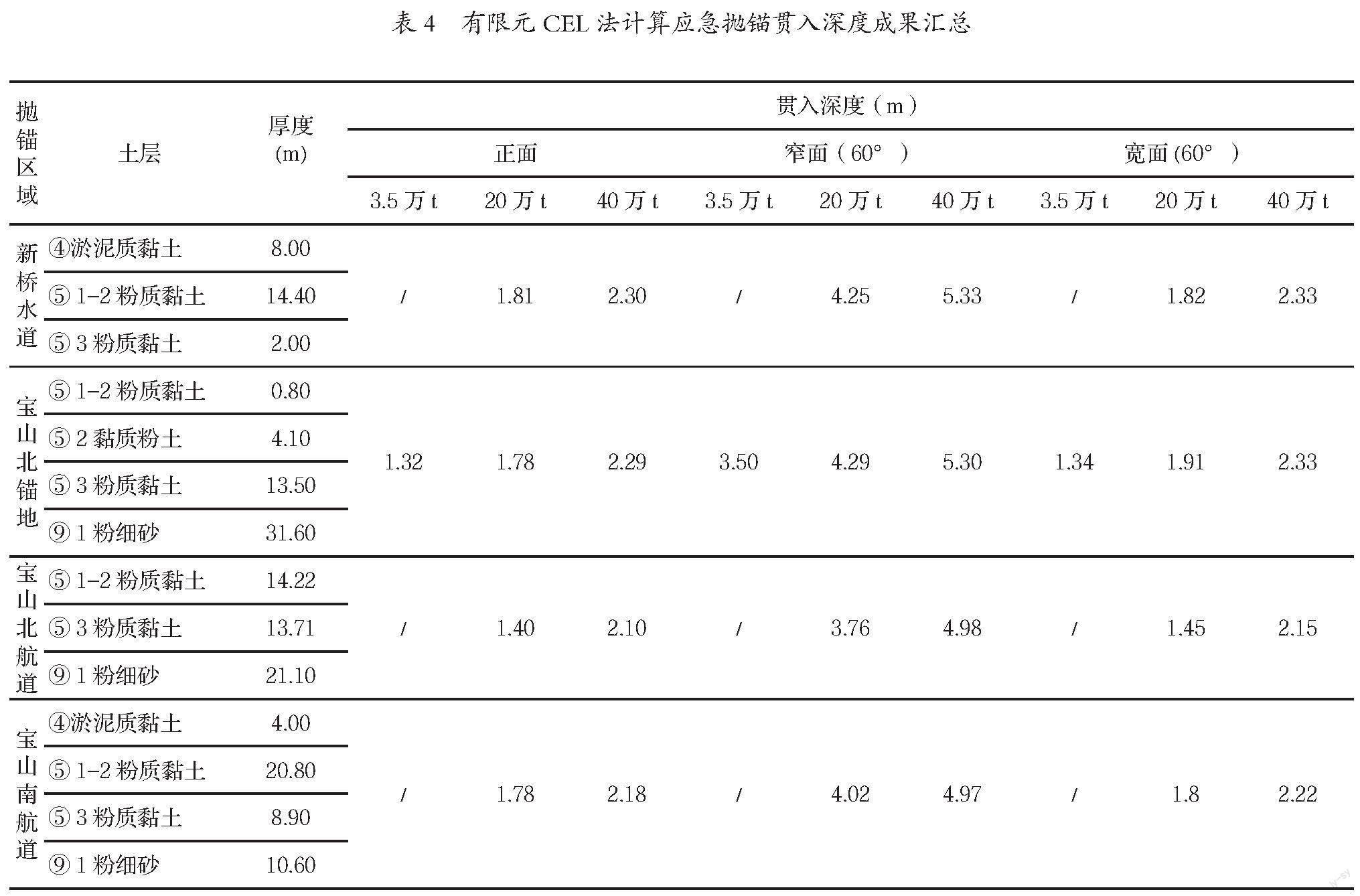
本次研究利用有限元 CEL大变形分析法得到了隧道工程区域现状河床船舶应急抛锚贯入深度如计算成果见表4。

2.5 CEL 公式法与有限元CEL计算成果对比

从表1-表4计算结果可以看出：在20万吨级船舶13.35 t船锚贯入角度60°时，常规公式法计算的不同工程区域最大贯入深度在2.72～3.88 m之间，有限元CEL分析法计算的不同工程区域贯入深度在3.76～4.29 m之间；在40万吨级船舶18.8 t船锚贯入角度60°时，常规公式法计算的不同工程区域最大贯入深度在3.27～4.37 m之间，有限元CEL分析法计算的不同工程区域贯入深度在4.97～5.33 m之间。

总的看来，有限元CEL大变形计算方法得到的结果要大于常规公式法计算结果，尤其是在船锚斜向窄面贯入时，主要原因是常规公式法无法充分考虑横截面积和土层刚度的变化，计算结果一般相对偏小。

3 结 论

本文应用常规公式和有限元CEL大变形分析法，研究了代表船型和船锚在工程水域的应急抛锚贯入深度，主要结论如下：

1）相比于常规公式计算法，有限元CEL大变形法计算的结果相对较大，尤其是在船锚斜向窄面（60°）贯入的工况。

2）常规公式法的计算结果受不变土壤系数、横截面积等因素的限制，无法考虑贯入过程中土壤的竖向推力和横向推力的变化，计算结果一般相对偏小。

3）有限元CEL大变形计算方法考虑多层土壤刚度以及土壤刚度随土层变形增加后的折减，能提供精度相对较高的计算结果。

4）土层组成相对单一地区可采用常规公式法。

5）针对地层组成多变的地区建议采用计算过程更加客观、计算精度较高的有限元 CEL 方法。

参考文献

[1] 刘欢，冯梅芳，张文海．抛锚作业撞击海底管道的影响分析[J]．石油工程建设，2012， 38（1）：21-23+84.

[2] 李学东．船锚触底贯穿量计算方法[J]．中国航海，2016， 39（1）：85-87.

[3] 王懿．基于CEL 的船舶抛锚入泥深度分析[J]．石油机械，2014， 42（12）：44-47.