A New Scheme of the ARA Transform for Solving Fractional-Order Waves-Like Equations Involving Variable Coefficients

Yu-Ming Chu,Sobia Sultana,Shazia Karim,Saima Rashidand Mohammed Shaaf Alharthi

1Department of Mathematics,Huzhou University,Huzhou,313000,China

2Department of Mathematics,Imam Mohammad Ibn Saud Islamic University,Riyadh,11461,Saudi Arabia

3Department of Basic Sciences and Humanities,UET Lahore,Faisalabad Campus,54800,Pakistan

4Department of Mathematics,Government College University,Faisalabad,38000,Pakistan

5Department of Mathematics and Statistics,College of Science,Taif University,P.O.Box 11099,Taif,21944,Saudi Arabia

ABSTRACT

The goal of this research is to develop a new,simplified analytical method known as the ARA-residue power series method for obtaining exact-approximate solutions employing Caputo type fractional partial differential equations(PDEs)with variable coefficient.ARA-transform is a robust and highly flexible generalization that unifies several existing transforms.The key concept behind this method is to create approximate series outcomes by implementing the ARA-transform and Taylor’s expansion.The process of finding approximations for dynamical fractional-order PDEs is challenging,but the ARA-residual power series technique magnifies this challenge by articulating the solution in a series pattern and then determining the series coefficients by employing the residual component and the limit at infinity concepts.This approach is effective and useful for solving a massive class of fractional-order PDEs.Five appealing implementations are taken into consideration to demonstrate the effectiveness of the projected technique in creating solitary series findings for the governing equations with variable coefficients.Additionally,several visualizations are drawn for different fractional-order values.Besides that,the estimated findings by the proposed technique are in close agreement with the exact outcomes.Finally,statistical analyses further validate the efficacy,dependability and steady interconnectivity of the suggested ARA-residue power series approach.

KEYWORDS

ARA-transform;Caputo fractional derivative;residue-power series method;analytical solutions;statistical analysis

1 Introduction

Several real-life occurrences in thermodynamics,molecular biology,operations research,and other disciplines of materials research can be lucratively modelled using fractional derivatives [1–6].The principal motivation behind this is that realistic modelling of a core challenge requires not only the precise moment but also the preceding sequential schedule,which can be efficiently accomplished by utilizing fractional calculus[7,8].However,numerous applied science researchers have concentrated on fractional partial differential equations(PDEs)in designing procedures for interaction problems and discussing physical phenomena.Aside from that,estimated and analytical strategies for FDE solutions have been investigated [9,10].The subject of fractional initial value problems (IVPs) has captured the attention of academic researchers because it has the functionality of describing several capabilities of real-life manifestations within a more believable methodology than conventional PDEs.Many accomplishments have been attributed to the assumption of strategy presence and consistency in the fractional IVP framework[11].For additional scientific articles on fractional ordinary and PDEs emerging in various fields of scientific research,see[12–14].

In a given situation,the level of flexibility of the nonlinear system in contemporary calculus(such as conventional calculus) is greater than that of the local differential equations operator.Authors[15,16] encompass the following applications of computation.As a consequence,intellectuals place an elevated significance on the investigation of non-integer order differentiation and integration.Geometrically,the arbitrarily defined order derivatives,which are predominantly predefined integrals,describe the complete function’s concentration,or the entire global integration variety [17,18].The practise of academics has greatly boosted the efficiency of differential equations as well as quantitative and quantifiable scientific studies.It is worth noting that the following derivative operators were developed using conclusive essential methodologies.It is a well-established fact that there is currently no underlying solution to this problem.Consequently,the power law kernel has multiple interpretations.The Caputo fractional-order derivative (CFD) [19] is perhaps the most appealing underlying conceptualization.Dynamical formulae are notorious for being hard to address quantitatively or precisely.As a result,computational intelligence methodologies for evaluating the foregoing formulas have been constructed.Numerous intellectuals have mainly investigated computational perspectives to investigate fractional PDE under CFD[20,21].

Furthermore,owing to the quantitative intricacies of the fractional operators involved,figuring out the numerical method for fractional IVP processes can be occasionally challenging.In this context,computational and analytical strategies have been created and energized in order to explore the outcomes of various types of linear/nonlinear fractional IVP mechanisms.To reference a couple different ones: the Adomian decomposition method,Legendre polynomial,Lie symmetry analysis,Haar wavelet method,spectral collocation method,homotopy perturbation method,homotopy analysis transform method,reproducing kernel Hilbert space method,Bernoulli polynomials,B-spline functions,Chebyshev polynomials and the residue power series method,see[22–24].

In 2013,Omar Abu Arqub,a Jordanian mathematician [25],invented the residual power series method (RPSM).However,RPSM is an analytical procedure for tackling ordinary,partial,and fuzzy DEs,as well as fractional-order integro-DEs,which correlates with the Taylor’s series having the residual error function.It offers linear and nonlinear DE series strategies in the context of convergence series.For its inaugural moment,RPSM was used to develop solutions to fuzzy DEs in 2013.Arqub et al.[26] applied an efficient technique for addressing the solution of higher-order IVP.Arqub et al.[27]used the RPSM to consider numerous findings for dynamical fractional-order boundary value problems.El-Ajou et al.[28] expounded the novel recursive approach RPSM for establishing the solutions of the nonlinear fractional KdV-Burgers model.Later on,this dynamical scheme merged with several integral transforms to make it more comprehensive.It is a useful metaheuristic algorithm because it applies with the help of closed-form functional information.In the scenario of nonlinear challenges,obtaining a solution in closed form is unattainable,and determining the series coefficients is a tough challenge.To address the shortcomings of the classic PSM,an optimized version of the PSM is introduced that treats the coefficient values as transmogrified operations that pursue a set of regulations and are ascertained by recurrence connections.For more details on RPSM,see[29–31].

In 1780,the French mathematician and physicist P.S.Laplace [32,33] proposed the integral transform.In 1822,J.Fourier [34] invented the Fourier transform.Laplace and Fourier transforms are the cornerstone of operations and maintenance interpretation,a strand of mathematical concepts with enormously potent implementations not just in mathematical modeling but also in different scientific fields such as thermodynamics,technology,cosmology,and so forth.This research is based on the implementation of the ARA Ts (ARA Ts),an innovative integral transform,introduced by Saadeh et al.[35].This transform is an influential and multi-functional generalization that consolidates several configurations of the conventional Laplace transform,including the Sumudu transform [36],the Elzaki transform [37],the Natural transform [38],the Yang transform [39] and the Shehu transform[40].

Numerous publications have been written to explain dynamic processes that can be induced and propagated in a variety of concentrations and configurations.The majority of academics have concentrated on minimizing the fundamental formulae of varying concentration models to evolution problems in the pattern of PDES such as the Swift-Hohenberg model (KdV) equation,Burger equation,Black-Scholes model,Boussinesq equation and so on[41–44].

Another development of the RPSM is assembled in this article by acclimating the ARA Ts[35,45]to the RPSM technique[25,26].In this article,the new framework,ARA-residual power series method(ARARPSM),is used to effectively resolve fractional-order PDEs.Furthermore,the detailed explanation of the nonlinear fractional-order PDEs is outlined below:

· The ARARPSM is an efficacious approach and a novel method for obtaining numerical approximations to dynamical fractional PDEs in series pattern.The series coefficients can be ascertained quickly by employing the notion of limit at ∞,which also helps in saving time and resources when compared to earlier traditional methods.

· Five problems are analyzed statistically to identify the reliability and robustness of the suggested technique.Furthermore,analytical findings are also compared with the existing results and are in agreement with the exact findings and several other techniques.

· Diagrammatically,relevance is indeed discovered for multiple fractional-order derivative attributes and the statistical performances of the mean absolute deviation,mean deviation,Theil’s inequality coefficients,and semi-interquartile range.Hence,the methodology is accurate,easy to employ,not influenced by supercomputing iterations of inconsistencies,and doesn’t necessitate an enormous amount of memory storage or time.

· This technique,unlike the conventional power series technique,somehow doesn’t entail identifying the coefficient values of the commensurate terms or the application of a recursion connection.The suggested restriction concept-based methodology shows series coefficients but not fractional derivatives,similar to the RPSM.Unlike RPSM,which also demands numerous computations to quantify multiple fractional derivatives during the completion of the task successfully,only a very few computations are required to evaluate the coefficients.

2 Preliminaries

This section provides a number of interpretations,characteristics,and some helpful findings that form the foundation of the novel methodology.The ARA Ts is derived using the classic Laplace integral.In order to simplify the method for solving ordinary and partial DEs in the temporal domain,Saadeh et al.[35]proposed the ARA Ts in 2020.ARA is the identifier of the proposed transform;the term is not an acronym.It has some interesting properties,such as the ability to generate multiple transforms by varying the significance of the index m,which was also initiated in[45],a duality with the Laplace transform,and the ability to navigate the singularity at time zero.

Definition 2.1.([22])Forδ＞0,the Caputo derivative of the mappingΨ(u,t)is described as

whereJsignifies an interval and Jδtis the time-fractional Riemann-Liouville integral operator orderδ＞0 stated as

Definition 2.2.([35])The ARA Ts of order m of the continuous mappingΨ(u,t)on the intervalJ×[0,∞)for t,is stated by

In the assertions that follow,we list a few ARA Ts ation fundamentals[35]that are crucial to our studies.

Suppose that there are two continuous mappingsΨ(u,t) and(u,t) defined onJ×[0,∞) for which the ARA Ts exists,then we have

Theorem 2.3.([25]) Assume there is a mappingΨ(u,t) with fractional power series (FPS)representation at time t=0,is defined as follows:

For continuous mappingsΨ(u,t) andDtmδΨ(u,t) defined onJ×[0,∞),then the coefficients(u)have the following formulation:

Theorem 2.4.([46])Suppose there is a continuous mappingΨ(u,t)defined onJ×[0,α]for which the ARA Ts for the variable t occurs and is expressed by the FPS form

Then

Remark 1.(a)Theℓthtruncated series of the series interpretation(1)is stated as follows:

(b)For the ARA Ts of order two of the mappingΨ(u,t)has the series interpretations(1),then the ARA Ts of order one can be written as follows:

and theℓthtruncated series is stated as follows:

(c)The inverse of the ARA Ts of order two for the FPS(1)is presented as follows:

Theorem 2.5.([46])Assume that there is a continuous mappingΨ(u,t)defined onJ×[0,α]for which the ARA Ts for the variable t holds.Also,suppose thatG1has the subsequent series formulation:

whereCm(u)=DmδtΨ(u,0).

3 Configuring Series Findings of FPDEs

In this section,the new framework,ARARPSM,is used to effectively resolve fractional-order PDEs of the form:

subject to the initial settings

whereϒusignifies the nonlinear term relative to u of orderr1,whileDtδdenotes the CFD of orderδandΨ(u,t)is the known function depending on variable u and t,respectively.

This part explains the ARA-RPS approach to addressing time-fractional PDEs.The proposed method relies on Taylor’s expansion to generate solitary solutions after applying the ARA Ts to the governing formulation.

Taking the initial value problem(IVP)(7)and(8),we implement the ARARPSM.

Apply the ARA Ts of order twoG2on both sides of the equation with respect to the variable t on(7)

In view of assertion(vi)and the initial conditions(8),then(9)reduces to

Suppose that the respective series conceptions correspond to the ARA-RPS solution of formula(9)has the following form:

and

Making the use of assertion(vii),we have

or accordingly

Now,assertion(v)provides that

Employing assertion(iv),we attain

Assertions(ii)and(vii)lead to

Therefore,the ARA-RPS findings of(10)has the series formulations:

and theℓthtruncated series expansion of(15)and(16)have the following interpretations:

To determine the parameter estimates of series developments in (17) and (18),we describe the ARA-residual component of(10),as shown

and the truncatedℓthresidue function is

Multiplying both sides of (18) by sℓδ+1,ℓ=2,3,...and applying the limit as s∞will enable you to identify the coefficientsm(u),m ≥2 in the series expansion(20).After that,we haveℓ=2,3,...

The ARA-RPS solution can be found by releasing the evidence below:

(a1)G2Res(u,s)=0,u ∈J,s＞0,

In order to achieve the solution of the IVP(7)and(8)in the feature space,the achieved coefficientsm(u) are supplemented in the series findings (12),and then the inverse ARA Ts of order twoG-12is used.

4 Test Examples

Here,we take into consideration three well-known and significant time fractional PDEs with varying coefficients challenges in order to illustrate the effectiveness and appropriateness of ARARPSM.

Example 1.Assume the subsequent nonlinear time fractional(1+1)wave like equation[47]:

whereδ∈(0,1],u ∈R and t ≥0 supplemented with initial conditions

Proof.Implementing the ARA Ts of order twoG2on(21),we have

It follows that

After simplification,(24)reduces to

Suppose that the ARA-RPS result of(25)has the subsequent series expression:

and theℓthtruncated series of the expansion(26)and(27)are

Conducting product both sides of(29)by s and applying the limit as s∞,yields

In view of the following assumption,we have

and the initial settings mentioned in (22),we deduce that0(u)=Ψ(u,0).Therefore,the series expression stated in(29)reduces to

Therefore,we have

It follows that

Considering assertion(v)provides that

Making the use of assertion(iv),gives

Making the use of assertion(ii)and(vii)lead us

Therefore,the ARA-RPS findings of(25)has the subsequent series formulations:

and theℓthtruncated series of the expansions(31)and(32)have the formulation

Furthermore,we classify the ARA-residue function of(25),then

and theℓthARA-residual mapping of(35)is

Utilizing the fact that

In order to evaluate the second unknown coefficient2(u)by inserting the second truncated seriesinto the second ARA-residual functionG2Res2(s)to find

Plugging

in(38)and simple computations yield

whereφ=0,φ=andψ=After simplification and solvingRes2(u,s)=0 for2(u),we have

Revisiting the analogous process,we can evaluate the coefficients of the series(26)as follows:

Hence,the seventh approximate solution of(26)is

Applying the inverse ARA TsG2-1on (38),we attain the seventh-order approximate solution in the original space which takes the form

For integer-order solution,the approximated solution(39)reduces to

It is worth noting that the integer-order solution (40) coincides with the result proposed by Khalouta et al.[47].

Example 2.Assume the subsequent nonlinear time fractional wave-like equation[47]:

whereδ∈(0,1],u ∈R and t ≥0 supplemented with initial conditions

Proof.Implementing the ARA Ts of order twoG2on(41),we have

It follows that

After simplification,(44)reduces to

Suppose that the ARA-RPS result of(45)has the subsequent series expression:

Here,the expansions in(46)ℓthtruncated series have the relatively similar reasoning as in Example 1 and result in the formation

Introducing theℓthARA-residual function of(44),we have

Conducting product on both sides of(48)by sℓδ+1,ℓ=2,3,...and applying limit as s∞to attain the coefficientsm(u)in the series expansion(46)as follows:

Plugging the coefficients in the series expansion ofwe acquire the seventh ARAapproximate finding

Using the inverse ARA Ts of order twoG2-1on(49),we arrive at the seventh approximation in the original space,to attain

For integer-order solution,the approximated solution of(50)reduces to

It is worth noting that the integer-order solution (51) coincides with the result proposed by Khalouta et al.[47].

Example 3.Assume the subsequent nonlinear time-fractional(2+1)-heat equation[48]:

whereδ∈(0,1],u,v ∈R2and t ≥0 supplemented with initial conditions

Proof.Implementing the ARA Ts of order twoG2on(52),we have

It follows that

After simplification,(55)reduces to

Suppose that the ARA-RPS result of(56)has the subsequent series expression:

Here,the expansions in(57)ℓthtruncated series have the relatively similar reasoning as in Example 1 and result in the formation

Introducing theℓthARA-residual function of(57),we have

Conducting product on both sides of(59)by sℓδ+1,ℓ=2,3,...and applying limit as s∞to attain the coefficientsm(u)in the series expansion(57)as follows:

Plugging the coefficients in the series expansion ofwe acquire the seventh ARAapproximate finding

Using the inverse ARA Ts of order twoG2-1on(60),we arrive at the seventh approximation in the original space,to attain

For integer-order solution,the approximated solution of(61)reduces to

It is worth noting that the integer-order solution (62) coincides with the result proposed by Khan et al.[48].

Example 4.Assume the subsequent nonlinear time-fractional(3+1)wave-like equation[48,49]:

whereδ∈(0,1],u,v,w ∈R3and t ≥0 supplemented with initial conditions

Proof.Implementing the ARA Ts of order twoG2on(63),we have

It follows that

After simplification,(66)reduces to

Suppose that the ARA-RPS result of(67)has the subsequent series expression:

Here,the expansions in(68)ℓthtruncated series have the relatively similar reasoning as in Example 1 and result in the formation

Introducing theℓthARA-residual function of(67),we have

Conducting product on both sides of(70)by sℓδ+1,ℓ=2,3,...and applying limit as s∞to attain the coefficientsm(u)in the series expansion(68)as follows:

Plugging the coefficients in the series expansion ofwe acquire the seventh ARAapproximate finding

Using the inverse ARA Ts of order twoG2-1on(71),we arrive at the seventh approximation in the original space,to attain

For integer-order solution,the approximated solution of(72)reduces to

It is worth noting that the integer-order solution(73)coincides with the result proposed by[48,49].

Example 5.Assume the subsequent 2D nonlinear time-fractional wave-like equation[47]:

whereδ∈(0,1],u,v ∈R2and t ≥0 supplemented with initial conditions

Proof.Implementing the ARA Ts of order twoG2on(74),we have

It follows that

After simplification,(77)reduces to

Suppose that the ARA-RPS result of(78)has the subsequent series expression:

Here,the expansions in(79)ℓthtruncated series have the relatively similar reasoning as in Example 1 and result in the formation

Introducing theℓthARA-residual function of(79),we have

Conducting product on both sides of(81)by sℓδ+1,ℓ=2,3,...and applying limit as s∞to attain the coefficientsm(u)in the series expansion(79)as follows:

Plugging the coefficients in the series expansion ofwe acquire the seventh ARAapproximate finding

Using the inverse ARA Ts of order twoG2-1on(82),we arrive at the seventh approximation in the original space,to attain

For integer-order solution,the approximated solution of(83)reduces to

It is worth noting that the integer-order solution (84) coincides with the result proposed by Khalouta et al.[47].

5 Numerical Simulation and Performance Techniques

Here,the consequences of the approximate and exact solutions to the approaches presented in Examples 1–5 are evaluated graphically and numerically in this portion.In the context of an infinite fractional power series,it is critical to supply the approximation inconsistencies of the estimated solution provided by ARARPSM.To illustrate the precision and competence of ARARPSM,we used the residual,mean absolute deviation (MAD):MADTΨ(u,t)=Thei l’s inequality coefficient (TIC):TICTΨ(u,t)=variance adjusted for (VAF):VAFTΨ(u,t)=×100,EVAFΨ(u,t)=and semi-interquartile range(SIR):S.I.R=-×(Q1-Q3),whereQ1represents the 1st-quartile andQ3denotes the 3rdquartile,alongside their global depictions.

The approximate results produced using the suggested procedure and the accurate solving Examples 1–5 are compared in Figs.1–5a via a two-dimensional plot.From Figs.1–5a,it can be seen that the analytical seventh-order solutions atδ=0.45,0.55,0.65,0.75,0.85,0.95,and 1.0 congregate to the actual solutions atδ=1.Moreover,the presented strategy’s authenticity and appropriateness are confirmed by the fact that the seventh-order approximations atδ=0.1 interplay also with actual findings atδ=1.0.The potency of the suggested procedure is validated by the Tables 1–4,which show that the approximations are very close to the exact solutions.

Figure 1 : Graphical illustrations for Example 1.(a) Two-dimensional plots for various values of fractional-order in comparison with the exact solution.(b) Histogram plots on the mean,meandeviation,semi-interquartile range and standard deviation

Figure 2 : Graphical illustrations for Example 2.(a) Two-dimensional plots for various values of fractional-order in comparison with the exact solution.(b) Histogram plots on the mean,meandeviation,semi-interquartile range and standard deviation

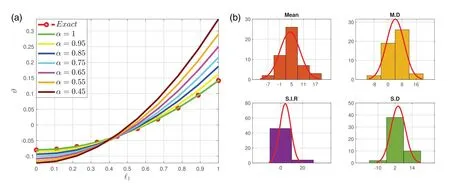
Figure 4 : Graphical illustrations for Example 4.(a) Two-dimensional plots for various values of fractional-order in comparison with the exact solution.(b) Histogram plots on the mean,meandeviation,semi-interquartile range and standard deviation

Figs.1–5b show the visual display of the statistical efficiency interventions along with their analysis on histograms for the results of the ARARPSM for the proposed dynamical systems.However,the ideal outcomes are depicted by exact and approximated values are discovered around 10-05-10-04,whereas the worst findings are represented in form of mean 10-04-1000,that are encountered around 10-04-1000.Achievements for M.D,S.I.R.,and SD are discovered around 10-08-10-05,respectively.The effectiveness of the ARARPSM,which is based on statistical formulation and solves the system dynamics in Examples 1–5,can clearly be seen to be valuable and worthwhile.For the dynamical framework Examples 1–5,indicating the wave-like and heat models,key parameters on the computation of global operators,such as MAD,EVAF,and T.I.C for numerous implementations analysis of the suggested ARARPSM are reported in Table 5.Hence,the MED terms of global TIC,MAD and EVAF physical quantities reside 10-7-10-8,10-9-10-10,and 10-9-10-10,respectively,whilst the global S.I.R formula of TIC,MAD and EVAF reside 10-5-10-6,10-9-10-10,and 10-9-10-10,respectively for Examples 1–5 dynamical framework.The correlation has proven that the indicated method and [29,47–49] produce the same results,demonstrating the efficiency and dependability of the ARARPSM.

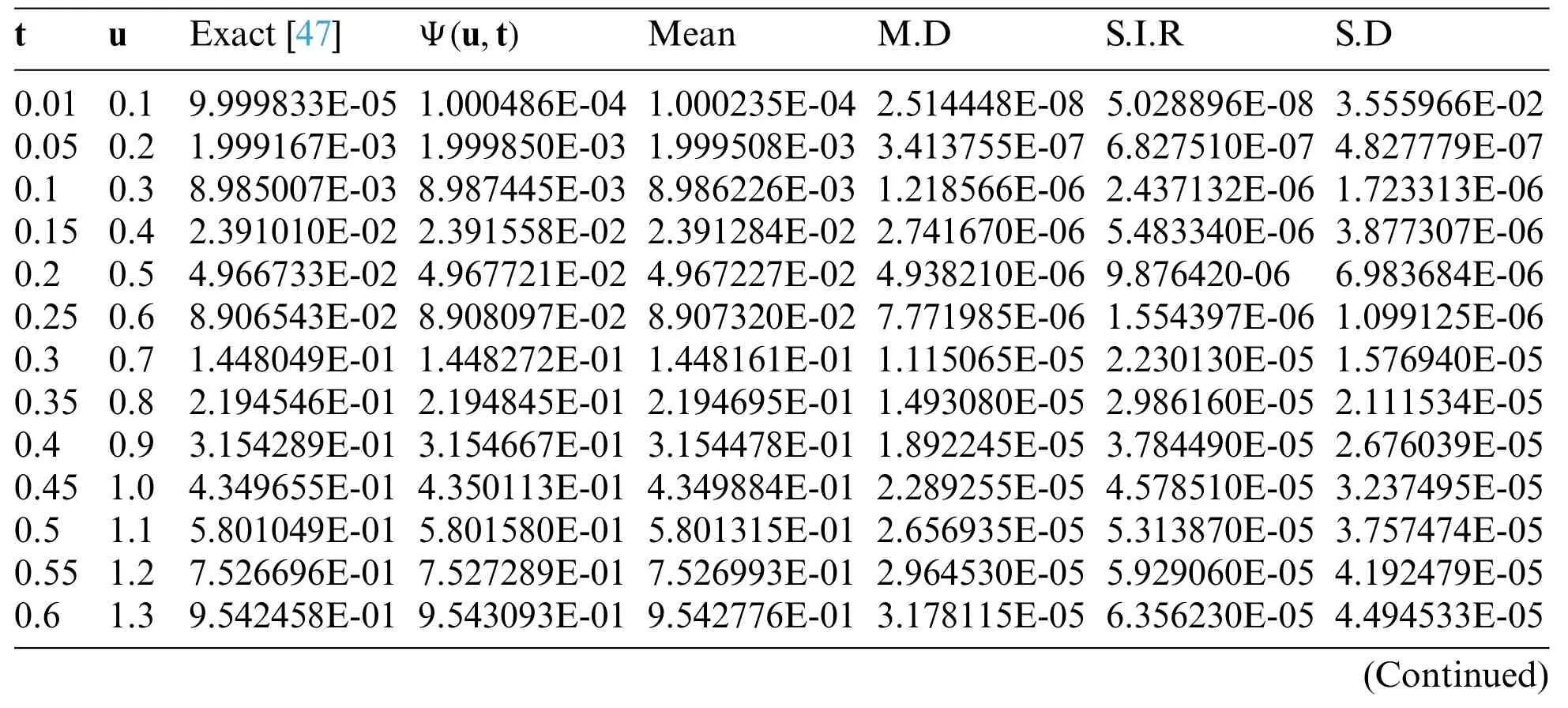
Table 1 :Comparison of statistical data analysis presentations of the time-fractional nonlinear(1+1)wave-like system in Example 1 that depend on the fractional-order and averages such as mean,mean deviation,semi-inter quartile range,and standard deviation with different values of t,u and the results proposed by[47]

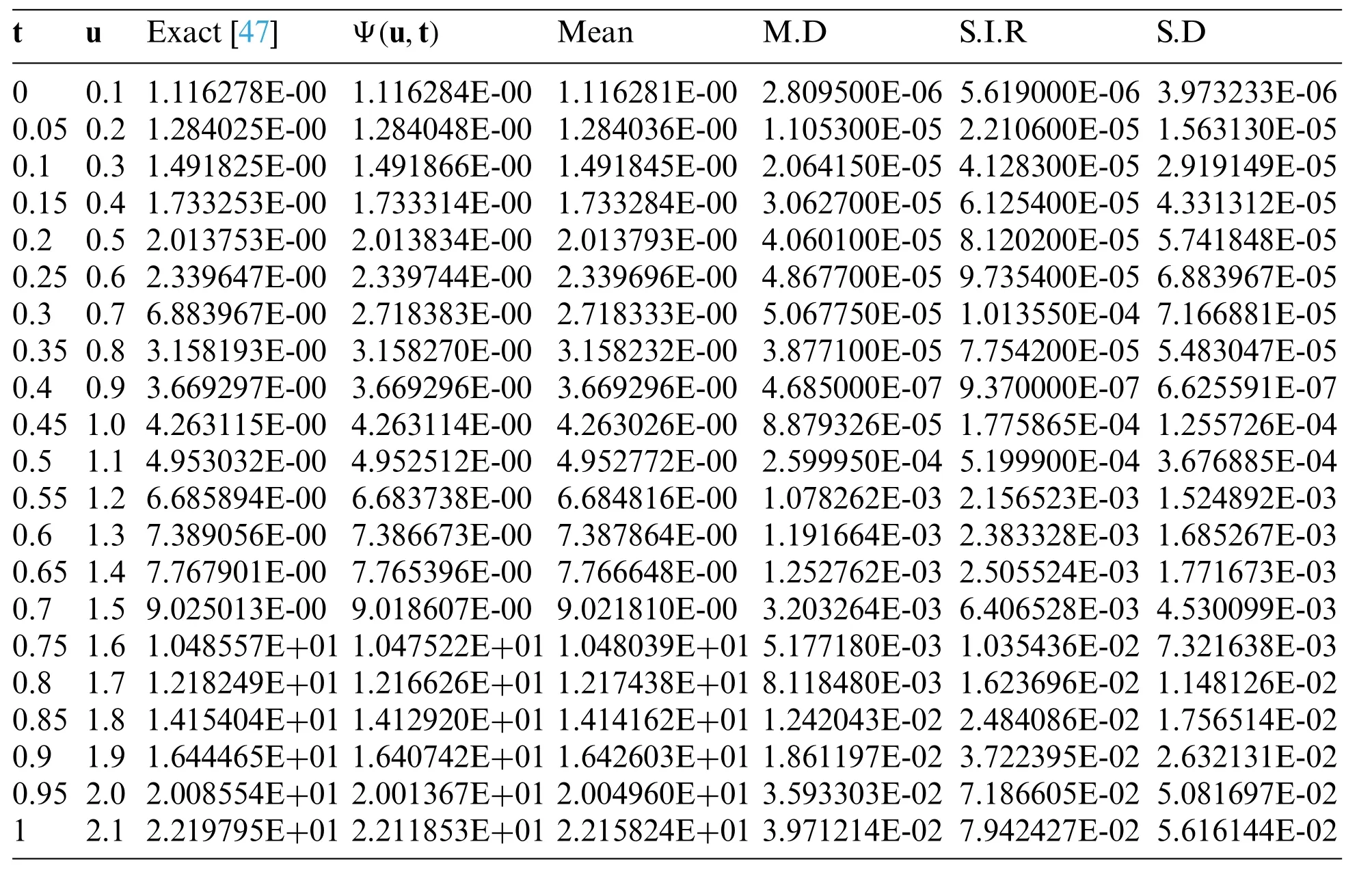
Table 2 :Comparison of statistical data analysis presentations of the time-fractional nonlinear wavelike system in Example 2 that depend on the fractional-order and averages such as mean,mean deviation,semi-inter quartile range,and standard deviation with different values of t,u and the results proposed by[47]

Table 3 : Comparison of statistical data analysis presentations of the time-fractional nonlinear (2+1) heat system in Example 3 that depend on the fractional-order and averages such as mean,mean deviation,semi-interquartile range,and standard deviation with different values of t,u and the results proposed by[48]

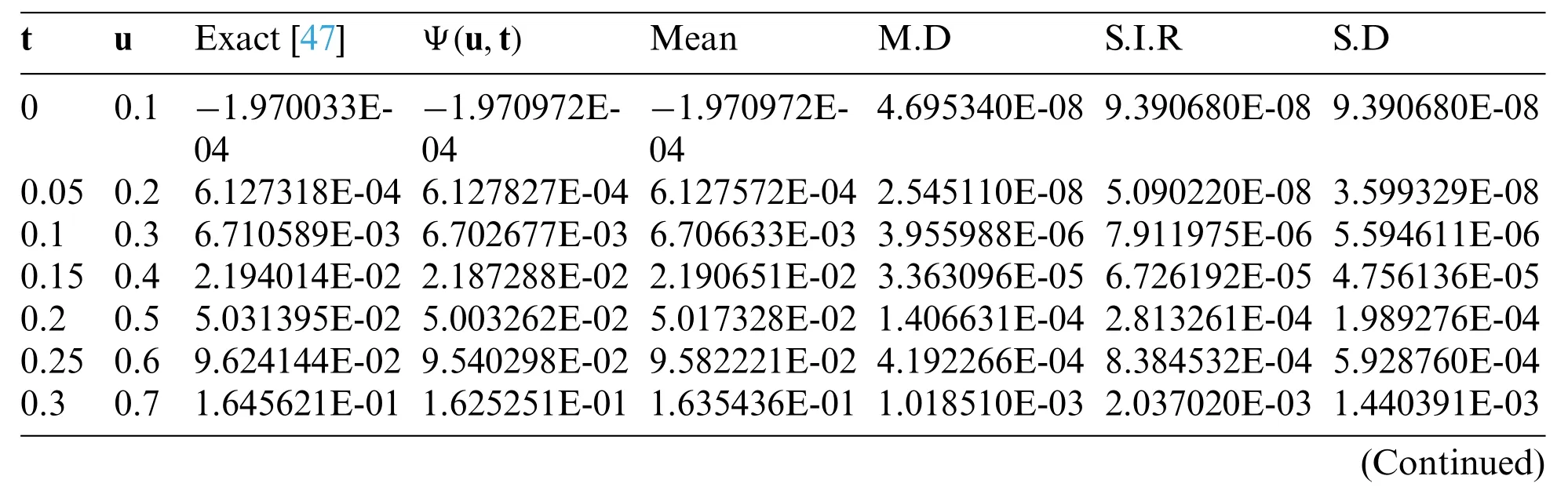
Table 4 :Comparison of statistical data analysis presentations of the time-fractional nonlinear(3+1)wave-like system in Example 4 that depend on the fractional-order and averages such as mean,mean deviation,semi-inter quartile range,and standard deviation with different values of t,u with v=w=0.1 and the results proposed by[48,49]

Table 5 :Comparison of statistical data analysis presentations of the time-fractional nonlinear wavelike system in Example 5 that depend on the fractional-order and averages such as mean,mean deviation,semi-inter quartile range,and standard deviation with different values of t,u with v=0.2 and the results proposed by[47]

Figure 5 : Graphical illustrations for Example 5.(a) Two-dimensional plots for various values of fractional-order in comparison with the exact solution.(b) Histogram plots on the mean,meandeviation,semi-interquartile range and standard deviation

The accuracy,exactness,and efficacy of the interconnected supercomputing algorithms of ARARPSMA for tackling the nonlinear wave-likeand heat-like systems are further indicated by standard measures such as G-TIC,G-MAD,and G-EVAF that are similar to their optimal setting.

Eventually,the major aspects of the ARA-PSM are as follows,as shown by the numerical,graphically and statistical outcomes: The suggested approach is a methodical,potent,and essential component for fractional-order PDEs estimated and exact solutions.The resilience of the mechanism lies in the fact that the presented strategy requires very few estimations than established computational models and is therefore more precise and cost-effective.In comparison to the variational iteration mechanism and the Adomian decomposition technique,the envisaged technique has the opportunity that it can help address computational complexity avoiding the He’s polynomials or Adomian polynomials.The proposed method is founded on a latest iteration of Taylor’s series that yields a convergent series as a solution.When determining the coefficient values for a succession such as the RPSM,the fractional derivatives must be calculated every time.We only require to perform a handful calculations to obtain the coefficients because ARARPSM only necessitates the idea of an infinite threshold.The relatively high level of exactness has been affirmed by the statistical analysis.To lesser estimations and iterative process actions,we came to the conclusion that the envisaged methodology is a practical and effective approach for tackling some categories of fractional-order PDEs.

6 Conclusion

In this paper,we presented a novel methodology for addressing fractional-order PDEs with variable coefficients in the context of a Caputo fractional derivative employing the ARA Ts and RPSM.Using the ARARPSM,we were able to address several dynamical fractional PDEs as well as illustrate a novel algorithm regarding them.Statistical or mathematical outcomes serve as evidence of the ARARPSM’s effectiveness.Complex nonlinear systems’objective measurements for Examples 1–5 statistical data analysis comparison have been provided in Table 6,which shows how the measure of dispersion has a significant impact on the proposed findings.These graphs and tables show that the ARARPSM’s approximations and the corresponding exact solutions are in good accordance with each other.Additionally,the MAD,TIC and EVAF formulation significance levels confirm the effectiveness of tackling the multidimensional fractional-order PDEs.Its accuracy and value are verified by assertions made utilizing statistical identifiers for various independent implementations employing the suggested ARARPSM predicted on the mean,mean deviation,S.I.R and S.D infiltrators.The error estimates for the projected framework range from 10-6to 10-9.The supremacy and efficacy of the comprehensive simulation for ARARPSM addressing the fractional PDES are also revealed by global measures such as G-TIC,G-MAD,and G-EVAF that are connected to their simultaneous optimization.The most important aspect of this procedure is that there are no minor or major tangible parameterized assumptions in the concern.Finally,it is applicable to both tenuous and powerfully multidimensional challenges,tackling several of the underlying limitations of classical variational methods.Based on the consequences obtained,we deduced that our proposed methodology is easy to execute,reliable,versatile and convenient.In the future,the algorithmic ARARPSM functionalities will be capable of tackling epidemiological research[16],complex nonlinear PDES[31,44]and fluidflow problems[50].

Acknowledgement: The researchers would like to acknowledge the Deanship of Scientific Research,Taif University for funding this work.

Funding Statement:The authors received no specific funding for this study.

Author Contributions:All authors read and approved the final manuscript.

Availability of Data and Materials:No data were used to support this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.