基于CKF-SLAM改进的无人水下航行器动态目标跟踪算法研究

都立立,邢传玺,万志良,李聪颖

(云南民族大学 电气信息工程学院,云南 昆明 650500)

在水下侦察领域,对动态目标进行跟踪是至关重要的研究课题.传统动态目标跟踪技术需要将实时数据与已知先验数据进行匹配才能实现,但在实际匹配过程中容易导致大幅偏差.文中可在无先验信息[1]的情况下,即在未知水下环境中,UUV动态目标跟踪在完成对自身位置定位与周围环境建图[2]的同时,探测估计动态目标的轨迹与位姿,整个运动过程中一直对动态目标进行跟踪.前者为SLAM问题,后者为目标跟踪问题[3].

目前在动态目标跟踪的问题上,主要集中在基于卡尔曼滤波类[4]方法.扩展卡尔曼滤波(extended Kalman filter,EKF)[5]SLAM算法,是一种最小均方差估计方法,将非线性系统利用泰勒级数一阶展开线性化,再进行线性卡尔曼滤波.EKF-SLAM算法简单易于实现并且在未知环境特征点较少时,UUV实际轨迹可以逼近理想的轨迹,但当未知环境中的特征点增加时,UUV实际轨迹和理想轨迹偏差较大,因此该算法只适合应用在环境特征点少的小区域环境.无迹卡尔曼滤波(unscented Kalman filter,UKF)[6]SLAM算法,该算法利用高斯随机变量来近似表达状态分布,用一组确定性采样得到的Sigma点来逼近,提高变量的平均值和方差,精度逼近二阶泰勒.UKF-SLAM算法在精度上有所提高,计算复杂度上因无须计算雅克比矩阵,因此更容易实现,但同样不适用于庞大复杂的环境.容积卡尔曼滤波(cubature Kalman filter,CKF)[7]SLAM算法,该算法是在三阶球面-容积变换规则下,提取容积样本点集,用来描述后验状态变量的统计特征,并由先验状态估计平均值和方差.CKF-SLAM算法的容积样本点集的权重比非负,保证在计算高斯积分时滤波性能和数值稳定,但也存在算法实时性不高、计算量大以及在面对动态目标物跟踪精度较低的问题.

基于以上内容,提出平方根容积卡尔曼滤波SLAM的UUV动态目标跟踪算法.该算法将UUV自身位姿、特征地图的估计和目标位姿三者相互耦合构成一个整体,确保了各个状态之间的关联性,并且随机函数的均值和方差采用容积准则下数值积分法计算,平方根因子对系统进行更新.结果表明,提高了UUV在未知水下环境对自身定位与动态目标跟踪能力.

1 同步定位地图构建和动态目标跟踪问题描述

1.1 SLAM问题的概率描述

UUV在水下环境实现同步定位与建图需要明确2个问题：首先是机器人在什么地方,即定位;其次是机器人周围环境是什么,即建图.两者的完成需要提取并组合侧扫声呐获取的未知环境信息和UUV内部的里程计和IMU单元获取的自身位姿信息,在移动的同时完成环境地图的构建并且持续的对自身的位置的预测、优化和更新[8].图1为SLAM系统结构框图.

图1 SLAM系统结构框图

UUV运动模型、观测模型为

(1)

Zk=H(Xk)+δk.

(2)

则SLAM数学描述为

(3)

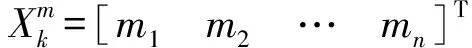
(4)

(5)

1.2 同步定位地图构建和动态目标跟踪问题描述

在未知环境中,运动状态下的UUV识别到目标物并进行跟踪,整个过程需要将UUV自身位姿、环境地图特征的估计和目标位姿[9]3者建立对应关系.因此要建立UUV和目标物各自的运动方程和观测方程,运动模型负责预测系统的状态,观测模型则根据地图特征点观测信息和目标物观测信息对系统状态进行更新.图2为UUV动态目标跟踪的系统框图.

该系统包含运动模型和观测模型[9].系统运动模型为

(6)

Zk=H(Xk)+δk.

(7)

图2 UUV动态目标跟踪系统框图

因此用概率估计来描述同步定位地图构建与动态目标跟踪问题为

(8)

(9)

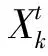
2 无人水下航行器动态目标跟踪算法

2.1 平方根容积卡尔曼滤波SLAM算法

该算法对CKF算法中计算复杂的部分进行改进,利用3阶容积准则选取m个相同权值的容积点[10]来近似计算,再利用数值积分法计算非线性方程模型的后验状态估计平均值和方差,并对协方差矩阵的平方根因子进行更新[10],减少了计算量,提高了系统的运行效率和计算结果的精度.

利用三阶容积准则计算高斯加权积分

(10)

(11)

整个算法分为预测阶段和更新阶段,图3为SRCKF-SLAM算法框图.

2.2 基于平方根容积卡尔曼滤波SLAM的无人水下航行器动态目标跟踪算法

该算法流程图如图4所示,处理过程分为3步：预测、数据关联和更新[11].预测阶段将误差协方差矩阵分解,计算容积点信息矩阵和先验概率估计,并对当前时刻系统状态和误差协方差矩阵的平方根因子预测[12],最终推算UUV和目标的位姿信息.数据关联包含3种关系：外部传感器单元获取的信息和UUV自身传感器单元获取数据[13]之间关系;UUV自身位姿状态和环境地图特征之间关系;环境地图特征数据之间的关系.同时数据关联阶段解决两方面问题：分别计算出UUV和目标的观测值,并和其实际观测值比较;筛选和剔除可能存在的伪观测值.更新阶段是在观测信息通过数据关联环节后计算观测向量后验概率和更新系统状态信息、误差协方差平方根因子[14].

图3 SRCKF-SLAM算法框图

图4 SRCKF-SLAM目标跟踪算法流程图

根据上述分析可得该算法的简要步骤为：

step 1 前一时刻到当前时刻为例,乔列斯基分解误差协方差阵Pk-1得

(12)

step 2 求解容积点矩阵[15]和其经过状态方程的容积点、再预测系统状态

(13)

式中,(i=1,2,…,m,m=2n).

(14)

(15)

step 3 UUV位姿预测和误差协方差矩阵的平方根因子预测

(16)

(17)

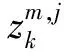
(18)

(19)

式中,mi表示探测到的环境特征;Rm和Rt表示误差信息矩阵;Zmi(k|k-1)和Zt(k|k-1)表示观测数据值;C(Zmi(k|k-1),Zmi(k|k-1))和C(Zt(k|k-1),Zt(k|k-1))表示观测数据值对应的误差信息矩阵;查χ2表获取γ.

step 5 再进行观测更新

(20)

(21)

step 6 计算卡尔曼增益矩阵Wk

(22)

(23)

(24)

(25)

(26)

step 7 更新系统状态信息矩阵、误差协方差平方根因子[17]

(27)

(28)

3 仿真实验及分析

3.1 仿真环境及参数设置

仿真环境1 使用AMD Ryzen 5 4600H with Radeon Graphics处理器,3.00 GHz 主频,16 GB 的RAM计算机,目标初始位置设为xp=[0,0,0,0],循环次数N=200,蒙特卡洛次数MC=300,滤波器个数为1,系统初始状态的方差和均值为P_0=diag([1×105,10,1×105,10]),x=[100,15,100,15],量测模型设置为sigma_r(1)=100,sigma_b(1)=80×e-3,这里仅说明了在二维平面的参数.UUV速度和控制速度分别为 3 m/s、0.3 m/s,转角误差为 2 rad,轮间距为 4 m.

仿真环境2 使用AMD Ryzen 5 4600 H with Radeon Graphics处理器,3.00 GHz 主频,16 GB 的RAM计算机,在开源仿真平台上,建立UUV目标跟踪仿真实验空间,目标从坐标(0,0)开始,沿确定的轨迹运行,UUV参数设置和仿真环境一相同,在整个仿真实验过程中UUV在完成同步定位与地图构建的同时对目标保持追踪状态.

对改进的SRCKF-SLAM-OT算法在以上2种仿真平台中仿真,UUV完成自身定位和对环境信息建图的同时,对动态目标一直保持跟踪状态,同时也和UKF-SLAM-OT、CKF-SLAM-OT这2种算法做了对比,比较这3种算法在定位精度和目标跟踪能力的差异程度.

3.2 仿真结果及性能分析

在2种仿真环境中,应用改进的SRCKF-SLAM-OT算法实现对动态目标跟踪实验,与目标实际路径进行比较、计算均方根误差进一步分析算法的性能,算法仿真结果如图5、6所示.

仿真结果表明,在降低计算复杂度和优化改进得到的SRCKF-SLAM-OT算法对目标物的跟踪轨迹基本吻合,反映出该算法实时性高和对目标物轨迹估计精度很高,但随着维度升高特征点采样数增多,算法估计路径和动态目标实际轨迹偏差会增大.

(a)路径跟踪(二维) (b)路径跟踪(三维) (c)RMS位置分析(二维)

(d)RMS位置分析(三维) (e)RMS速率分析(二维) (f)RMS速率分析(二维)图5 仿真环境1跟踪轨迹和均方根误差

(a)跟踪轨迹 (b)均方根误差分析图6 仿真环境2跟踪轨迹和均方根误差

3.3 3种算法对比分析

在仿真平台中,对SRCKF-SLAM-OT、UKF-SLAM-OT和CKF-SLAM-OT 3种算法分别在二维平面和三维空间中仿真,得到动态目标真实路径和3种算法目标估计路径,如图7、8所示.

由图可以看到实直线轨迹、虚线轨迹、双画线轨迹和点画线轨迹分别表示目标物真实轨迹、UKF、CKF和SRCKF算法目标估计轨迹.无论在二维平面还是三维空间中,3种算法的轨迹从设置的初始位置开始,均朝目标物运动方向进行跟踪,UKF的动态目标跟踪轨迹和实际轨迹的偏差[18]最大,其次是CKF的动态目标跟踪轨迹的偏差,而SRCKF算法动态目标跟踪轨迹与目标真实轨迹基本吻合,表明了该算法提高了UUV对动态目标物的跟踪能力.

(a)三种算法跟踪结果 (b)局部放大图图7 3种算法动态目标跟踪结果(二维)

(a)三种算法三维跟踪轨迹 (b)局部放大图图8 3种算法动态目标跟踪结果(三维)

(1) 定位与跟踪误差分析

在仿真平台中,对SRCKF-SLAM-OT、UKF-SLAM-OT和CKF-SLAM-OT 3种算法分别在二维平面和三维空间中进行目标在x和y方向的误差对比分析,如图9所示.

(a)目标在x方向误差对比(二维) (b)目标在y方向误差对比(二维)

(c)目标在x方向误差对比(三维) (d)目标在x方向误差对比(三维)图9 在x、y方向误差对比

由图可以看到无论在二维平面还是三维空间中,在x方向和y方向上均有SRCKF-SLAM-OT算法误差最小,其次是CKF-SLAM-OT算法误差,UKF-SLAM-OT算法误差[19]最大.表明了采用改进的SRCKF-SLAM-OT算法,提高了UUV自身定位精度和对动态目标跟踪能力.

(2) 均方根误差分析

在仿真平台中,对SRCKF-SLAM-OT、UKF-SLAM-OT和CKF-SLAM-OT 3种算法分别在二维平面和三维空间中,计算位置均方根和速度均方根来评价三种算法的估计效果,如图10所示.

(29)

(30)

由图可以看出无论在二维平面还是三维空间中,位置均方根误差和速度均方根误差[20]均有SRCKF-SLAM-OT算法均方根误差最小,其次是CKF-SLAM-OT算法均方根误差,UKF-SLAM-OT算法均方根误差最大.表明了采用改进的SRCKF-SLAM-OT算法明显提升了对动态目标估计的精度.

(a)位置均方根误差分析(二维) (b)速度均方根误差分析(二维)

(c) 速度均方根误差分析(三维) (d) 位置均方根误差分析(三维)图10 位置、速度的均方根误差对比

4 结语

为解决容积卡尔曼滤波SLAM算法存在的算法实时性不高、计算量大以及对动态目标物跟踪精度较低的问题,提出SRCKF-SLAM的无人水下航行器动态目标跟踪算法.该算法将UUV、环境地图特征和动态目标物三者构成一个整体,更具体的是对UUV位姿的估计、环境地图特征的估计和目标位姿的估计这三者互相耦合.建立UUV与动态目标各自的运动模型和观测模型,得到的信息经过预测阶段、数据关联阶段和更新阶段,并在更新阶段传递系统协方差矩阵的平方根因子.在3种算法跟踪轨迹仿真、定位与跟踪误差分析和均方根误差分析结果中,一致表明采用SRCKF-SLAM-OT算法,减小了计算复杂度,提高了UUV自身定位精度和动态目标跟踪能力,在水下侦察领域应用意义巨大.

改进的SRCKF-SLAM-OT算法在随着系统维度的升高,对目标估计轨迹与目标实际轨迹偏差增大的问题,将是今后研究的重点.