无穷时间不确定线性二次最优控制的乐观值模型
陈越奋, 郑 重
(1. 南京工业职业技术大学 公共基础课部, 江苏 南京 210023; 2. 信阳师范大学 数学与统计学院, 河南 信阳 464000)
0 引言
最优控制模型在组合投资[1]、生物系统[2]等领域中都有重要的应用。近年来,基于不确定性理论[3]的最优控制模型,在理论和应用上越来越受到学者们的重视。2010年,ZHU[4]首次提出了不确定最优控制的期望值模型,随后,CHEN等[5]研究了不确定随机最优控制问题,LU等[6]研究了分数阶不确定最优控制模型等。
乐观值准则反映的是以一定置信水平α的评价标准,优化不确定目标的乐观值的情况,能够很好地解释一些实际问题,这在工程技术和社会生活领域都具有重要的意义。例如,当学生的考试成绩出现了两极分化现象时,考察置信水平90%的学生考试成绩在70分以上,比仅考虑全班的平均分数更有价值。2013年,SHENG等[7]研究了乐观值准则下的有限时间不确定最优控制模型。本文在乐观值准则下,讨论具有折扣因子的无穷时间不确定线性二次最优控制模型。
1 预备知识
下面给出关于不确定性理论的一些基本概念。设Γ是一个非空集合,L是Γ上的σ-代数,称每一个Λ∈L为一个事件。
定义1[3]如果σ-代数上的集函数M满足:(1)(正规性)对全集Γ,M{Γ}=1;(2)(自对偶性)对任意的事件Λ,M{Λ}+M{Λc}=1;(3) (次可数可加性) 对任意可数的事件序列{Λi},有
则称M为不确定测度。此时,称(Γ,L,M)为一个不确定空间。
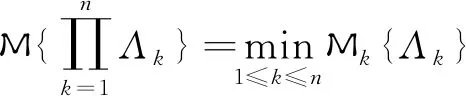
定义2[8]LIU过程Ct是指满足下面三个条件的不确定过程:(1)C0=0,几乎所有的轨道Lipschitz连续;(2)Ct具有独立稳态增量;(3) 对于时间t,增量Cs+t-Cs是一个具有期望值为0和方差为t2的正态不确定变量,其不确定分布是
(1)
定义3[3]假设ξ是不确定变量,且α∈(0,1],那么
ξsup(α)=sup{r|M{ξ≥r}≥α}
称为ξ的α-乐观值;
ξinf(α)=inf{r|M{ξ≤r}≥α}
称为ξ的α-悲观值。
定理1[9]假设ξ和η是不确定变量,且α∈(0,1],则有
1) 如果λ≥0,那么(λξ)sup(α)=λξsup(α),且(λξ)inf(α)=λξinf(α);
2) 如果λ<0,那么(λξ)sup(α)=λξinf(α),且(λξ)inf(α)=λξsup(α);
3) 如果ξ和η是独立的,那么
(ξ+η)sup(α)=ξsup(α)+ηsup(α),
(ξ+η)inf(α)=ξinf(α)+ηinf(α)。
2 不确定系统最优控制的乐观值模型
2.1 有限时间最优控制的乐观值模型
对于任意的0 (2) 式中: 定理2[7]假设J(t,x)在[0,T]×Rn上二次可微,则 -Jt(t,x)= (3) 式中:Jt(t,x)是函数J(t,x)在t处的偏导数,∇xJ(t,x)是函数J(t,x)在x处的梯度,且‖·‖1表示向量的1-范数,即对p=(p1,p2,…,pn), 考虑具有折扣因子的无穷时间不确定最优控制的乐观值模型: (4) 式中:ρ>0是折扣因子,其他变量同模型(2)。 下面利用不确定最优控制乐观值模型的最优性方程(3),给出具有折扣因子的无穷时间最优控制乐观值模型的最优性方程。 ∇xJ(t,x)τb(t,x,u)+Jt(t,x)+ (5) 式中:Jt(t,x)是函数J(t,x)对t的偏导数,∇xJ(t,x)是函数J(t,x)对x的梯度。 证明在t=0时刻,目标函数的现值为V(t,x)=e-ρtJ(t,x),可得 ∇xV=e-ρt∇xJ(t,x)。 将上式代入乐观值模型的最优性方程(3),即是 ρe-ρtJ(t,x)-e-ρtJt(t,x)= 进一步可得, (6) 将式(6)两端除以e-ρt并移项,可得乐观值模型的最优性方程(5)。证毕。 下面利用最优性方程(5),给出具有折扣因子的无穷时间线性二次最优控制的乐观值模型。 考虑以下具有折扣因子的无穷时间不确定线性二次最优控制的乐观值模型: (7) 式中:ρ>0是折扣因子,x(t)是状态变量,u(t)是控制变量,Ct是LIU过程,且x(0)=x0是初始状态。下面给出两个基本假设。 假设1 假设参数α(t),β(t),γ(t),δ(t),σ(t),η(t),F(t),G(t),G-1(t),H(t),L(t),M(t),N(t)是[0,∞)上的连续有界函数。 假设2 假设值函数J(0,x0)是[0,∞)×R上的二次可微向量函数,且F(t)≥0,G(t)>0。 定理4 在假设1和假设2的条件下,u*(t)是无穷时间线性二次最优控制乐观值模型(7)最优控制的充分必要条件是 (8) 式中:x是状态向量xt在t时刻与最优控制u*(t)对应的状态。函数Jx(t,x)=P(t)x(t)+Q(t),P(t)满足微分方程 (9) Q(t)满足微分方程 (10) 进一步地,乐观值模型(7)的最优值为 (11) 式中 (12) 证明(必要性) 由最优性方程(5),可得 H(t)x(t)u(t)+L(t)x(t)+M(t)u(t)+ Jx(t,x)[α(t)x(t)+β(t)u(t)+γ(t)]+ (13) 令 U(u)=F(t)x2(t)+G(t)u2(t)+H(t)x(t)u(t)+ Jx(t,x)[α(t)x(t)+β(t)u(t)+γ(t)]+ (14) 由于 此时u*(t)是模型(7)的最优控制,即 将式(14)代入式(13),可得 ρJ(t,x)=F(t)x2(t)+G(t)(u*(t))2+ H(t)x(t)u*(t)+L(t)x(t)+ Jx(t,x)[α(t)x(t)+β(t)u*(t)+γ(t)]+ σ(t)u*(t)+η(t)]|, (15) 将式(15)两边关于x求导,可得 Jxx(t,x)[α(t)x(t)+β(t)u*(t)+γ(t)]+ σ(t)u*(t)+η(t)]+ (16) 根据式(14)并结合式(16),可得 H(t)u*(t)-L(t)-Jx(t,x)α(t)- Jxx(t,x)[α(t)x(t)+β(t)u*(t)+γ(t)]+ σ(t)u*(t)+η(t)]+Jx(t,x)δ(t)|, (17) 此时令 λ(t)=Jx(t,x)。 (18) 因为J(t,x)是线性二次最优控制模型(7)的值函数,构造 λ(t)=P(t)x(t)+Q(t)。 (19) 将式(18)两边关于t求导,可得 (20) 将式(17)和式(18)代入式(20),可得 H(t)u*(t)-L(t)- P(t)[α(t)x(t)+β(t)u*(t)+γ(t)]- [P(t)x(t)+Q(t)]α(t)- (21) 将式(14)代入式(21),可得 ρQ(t)-P(t)γ(t)-Q(t)α(t)- (22) 另一方面,对式(19)两边关于t求导,可得 (23) 由式(22)和式(23),分别可得 求解上面的方程,可得P(t)和Q(t)的表达式,进而可知u*(t)是线性二次最优控制模型的最优控制。 (充分性)假设u*(t),P(t)和Q(t)分别满足式(8)、式(9)和式(10),下面证明u*(t)是最优控制。 根据最优性方程(5)可知,u*(t)满足方程: Jt(t,x)-ρJ(t,x)+F(t)x2(t)+ G(t)(u*(t))2+H(t)x(t)u*(t)+ L(t)x(t)+M(t)u*(t)+N(t)+ Jx(t,x)[α(t)x(t)+β(t)u*(t)+γ(t)]+ σ(t)u*(t)+η(t)]|=0。 (24) 因为值函数J(t,x)是二阶可微的,可设 进而有 {ρQ(t)-P(t)γ(t)-Q(t)α(t)-L(t)- 比较上述方程的两边,分别可以得到式(9)、式(10)和式(12)。 因此,可知u*(t)是方程(24)的解。由于目标函数是凸函数,方程(24)产生极小值,即u*(t)是乐观值模型的最优控制,从而得到模型(7)的最优值为 证毕。 下面将无穷时间不确定线性二次最优控制的乐观值模型应用到不确定环境下的广告投放问题。假设某商场希望以某一个置信水平α投放广告,获得最大的利润。为了建立数学模型,使用以下符号: α:给定的置信水平,且α∈(0,1]。 xt:时刻t的市场份额,且xt∈[0,1]; ρ:非负折扣利润率; Ct:假设投放的广告量服从典范Liu过程; x0:初始市场水平值; ut:时刻t投放的广告量,且ut≥0; r:正常数(r>0); δ:正常数(δ>0); v:对应于x=1的最大销售收入,vx表示xt∈[0,1]的收入函数; σ:常数扩散系数,且σ≥0。 不确定环境下的广告投放模型如下: (25) 定理5 假设J(0,x0)为不确定广告投放问题的利润函数,则J(0,x0)满足以下微分方程: 其中a由下式给出 证明由问题可知Jx(0,x)≥0。根据最优性方程(5),可得 (26) 对式(26)右端关于u求导,并令其为0,可得 (27) 将式(27)代入式(26)可得方程 (28) 假设上述解具有形式J(0,x0)=ax+b(a>0,b>0),那么Jx(0,x0)=a。将这些表达式代入式(28),可得下面方程 (r2a2+4aδ-4v+4ρa)xt+4ρb- (29) 从而可以得到最优性条件 r2a2+(4δ+4ρ)a-4v=0, (30) (31) 上述方程(30)和(31)的解(取值J(0,x0)≥0)为 进而得到最优的广告投放量 (32) 以及商场的最大利润J(0,x0)=axt+b。证毕。 研究了一类具有折扣因子的无穷时间不确定线性二次最优控制的乐观值模型。首先推导出无穷时间最优控制乐观值模型一般情形的最优性方程,然后利用不确定最优控制的最优性方程,得到了模型的最优控制,可以从约束微分方程解出。最后作为应用,利用最优性方程研究了一个不确定广告投放问题。本文中假设状态权矩阵是半正定的,控制权矩阵是正定的,下一步将考虑该模型的状态权矩阵和控制权矩阵均是不定的情形。
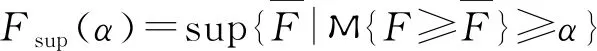

2.2 无穷时间不确定最优控制的乐观值模型
2.3 无穷时间不确定最优控制乐观值模型的最优性方程
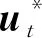
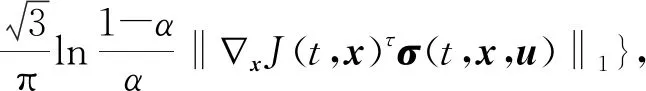
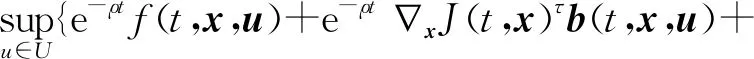

3 具有折扣因子的无穷时间不确定线性二次最优控制的乐观值模型
3.1 线性二次最优控制乐观值模型

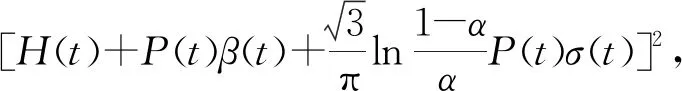
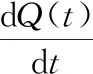
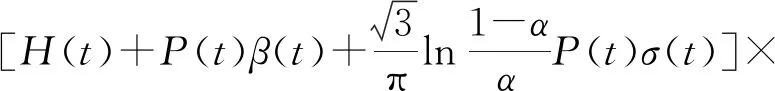
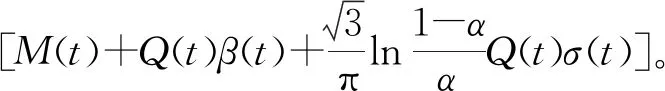
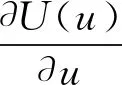
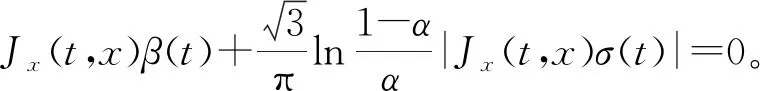
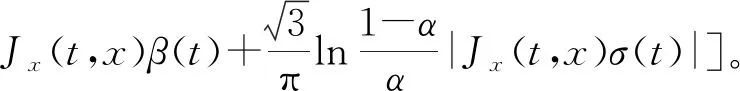
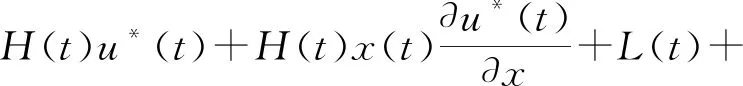

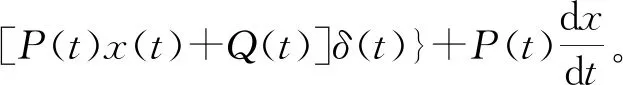
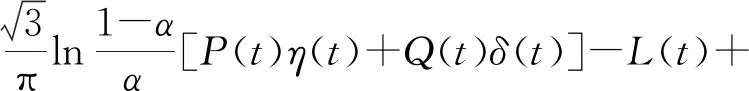
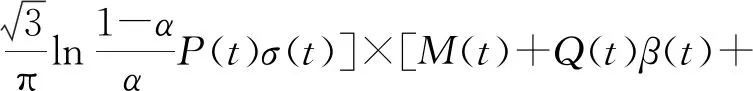

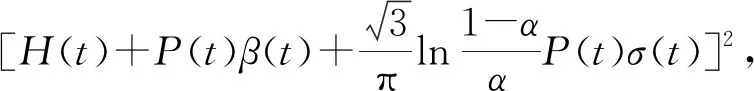
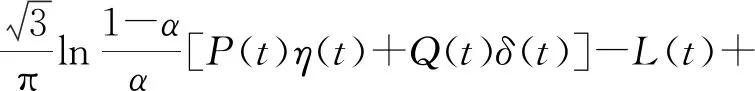
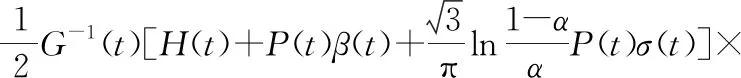
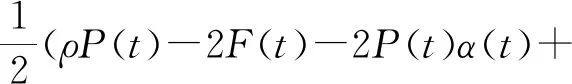

3.2 不确定环境下广告投放问题的应用

4 结束语

