导数及应用求解中的“误区警示”
侯有岐
(汉中市四○五学校,陕西 汉中 723312)
导数是研究函数的重要工具,在历年高考中都占据着重要的地位,而且这部分知识既有难度较大的填空题,也有计算繁琐的解答题.由于学生对一些概念理解不透、审题不严、考虑不周或忽视结论成立的条件等产生思维混乱,导致求解失误.本文对导数及应用求解中的常见误区分类例析,剖析其出错的原因,并给出警示,希望能引起同学们的高度重视.
1 对导数的定义理解不到位致错
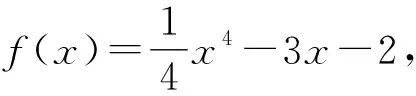
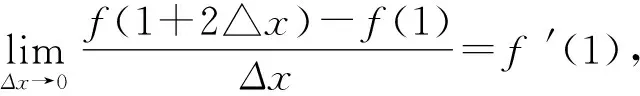
所以f′(1)=-2.
剖析在导数定义中,增量△x的形式是多种多样的,但无论如何变化,其实质是分子中x的增量与分母中x的增量必须一致,否则必须通过一些恰当的变形使之一致.本例分子中x的增量为2Δx(即1+2Δx-1=2Δx),而分母中x增量为Δx[1].
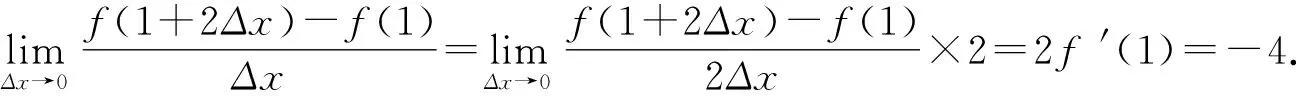
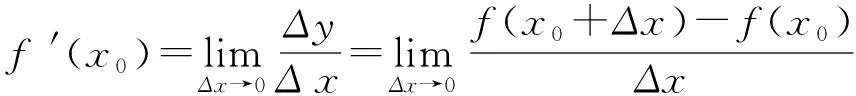
2 忽视函数的定义域致错
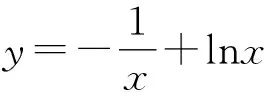
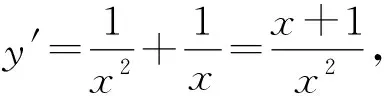
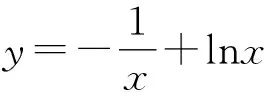
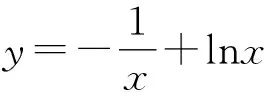
警示解决函数类问题一定要养成“定义域优先”的习惯,否则很容易造成解题错误.
3 复合函数的求导不彻底致错
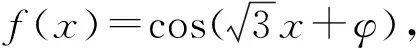
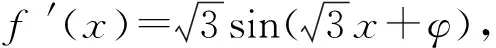
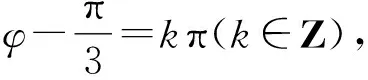
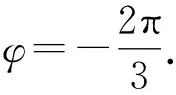
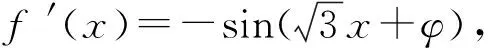
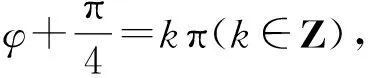
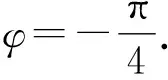
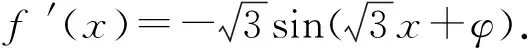
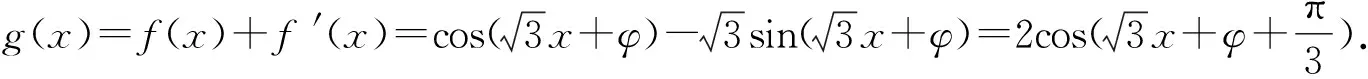
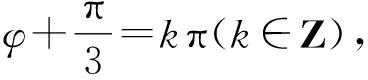
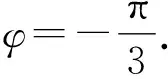
警示复合函数求导时,选择中间变量是关键,必须正确分析复合函数的复合层次,然后从外向里逐层求导,求导后,要把中间变量转换成自变量的函数.出错原因往往是由于在复合函数求导时,复合过程划分不彻底产生的.
4 混淆“过某点”的切线与在“某点处”的切线
例4 求过点A(2,-2),且与曲线f(x)=3x-x3相切的直线方程.
错解经检验点A(2,-2)在曲线f(x)上,求导得f′(x)=3-3x2,所以切线的斜率为f′(x)=-9,故切线方程为y+2=-9(x-2),即9x+y-16=0.
剖析错解混淆了“过某点”与“在某点”处的切线的概念,尽管点A在曲线上,但题目要求的是“过”点A的切线,因此应考虑A(2,-2)是切点和不是切点两种情况,所以用“切点待定法”求解.
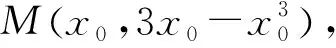
则在点M处的切线方程为
因为点A(2,-2)在切线上,将点A(2,-2)代入得
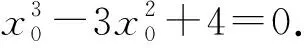
即(x0+1)(x0-2)2=0.
解得x0=-1或x0=2.
所以切线方程为y=-2或9x+y-16=0.
警示(1)曲线的切线不一定和曲线只有一个交点;(2)“在”某一点的切线和“过”某一点的切线是两个不同的概念;(3)“在”某一点的切线若有则只有一条,而“过”某一点的切线往往不只是一条,一般用“切点待定法”求解,如本题.
5 混淆“导数为0”与“有极值”的逻辑关系
例5已知函数f(x)=x3+3mx2+nx+m2在x=-1处取得极值0,则m+n=( ).
A. 4 B. 11 C. 4或11 D. 3或9
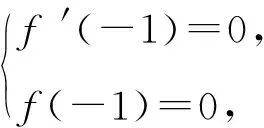
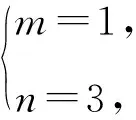
故m+n=4或11.故选C.
剖析错解对“导数为0”与“有极值”的逻辑关系分辨不清,把“极值点”等同于“导数的零点”,没有把求出的m,n值代入检验.事实上,f′(x)=0的点只是可导函数f(x)极值点的必要不充分条件.
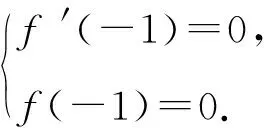
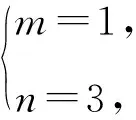
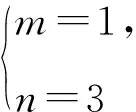
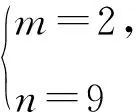
令f′(x)>0,得x<-3或x>-1;
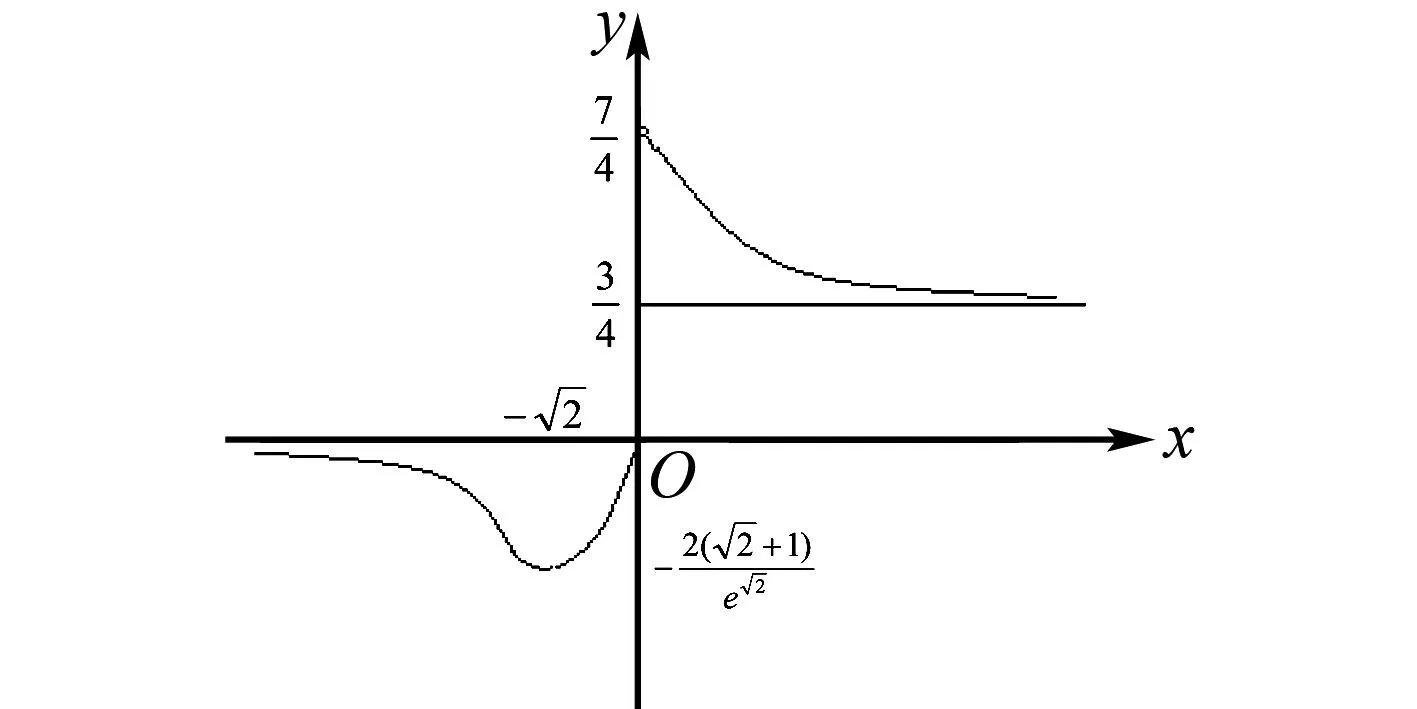
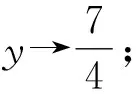
令f′(x)<0,得-3 所以f(x)在(-∞,-3),(-1,+∞)上单调递增,在(-3,-1)上单调递减,符合题意. 则m+n=2+9=11.故选B. 警示f′(x0)=0是可导函数f(x)在点x0处取得极值的必要不充分条件,导数为0的点只是可导函数存在极值的可疑点,若它的两侧导数异号,它才是函数的极值点;若它的两侧导数同号,则不为极值点,所以在求得导数为0的点后,还要进行检验,否则容易出错. 例6 已知函数f(x)=-x3+ax2+4x(a∈R),若f(x)在区间(0,2)上是单调递增的,求实数a的取值范围. 错解因为f(x)=-x3+ax2+4x(a∈R), 所以f′(x)=-3x2+2ax+4. 由于f(x)在区间(0,2)上单调递增, 所以有f′(x)>0在(0,2)上恒成立. 所以g(x)在(0,2)上单调递增. 故实数a的取值范围为(2,+∞). 剖析错误之处就是忽视了f′(x)=0的情况.事实上,当f′(x)在某个区间内的个别点处为零,其余点处为正(或负)时,f(x)在这个区间上仍然是单调递增(或递减)函数,故应令f′(x)≥0在(0,2)上恒成立. 正解因为f(x)=-x3+ax2+4x(a∈R), 所以f′(x)=-3x2+2ax+4. 由于f(x)在区间(0,2)上单调递增,所以有f′(x)≥0在(0,2)上恒成立. 所以g(x)在(0,2)上单调递增. 故实数a的取值范围为[2,+∞). 警示由函数的单调性、极值等问题求解参数的取值范围是高考命题的一个重点.解决此类问题的关键在于正确理解单调性、极值的概念和其求解、判断的方法.要注意以下细节问题: (1)f′(x)>0(f′(x)<0)(x∈(a,b))是f(x)在(a,b)上单调递增(减)的充分不必要条件.实际上,可导函数f(x)在(a,b)上为单调递增(减)函数的充要条件为:对于任意x∈(a,b),有f′(x)≥0(f′(x)≤0)且f′(x)在(a,b)的任意子区间上都不恒为0.因而这类题求出参数范围后,应对“=”成立的值进行检验,看是否符合题意;(2)解题中对“恒成立、能成立、恰成立”等概念区分不清也易致错. 当x=2时,f′(x)不存在,因此,f(x)在x=2处不可导. 所以f(x)无极值. 剖析在确定极值时,只讨论满足f′(x)=0的点x0附近导数的符号变化情况是不全面的,在导数不存在的点处也可能存在极值[2]. 当x=2时,f′(x)不存在,因此,f(x)在x=2处不可导. 但当x<2时,f′(x)>0;当x>2时,f′(x)<0,且函数f(x)在x=2处有定义. 所以f(x)在点x=2处取得极大值,且极大值为1. 警示可导函数的极值点一定是其导数为零的点;反之,导数为零的点不一定是该函数的极值点.因此,导数为零的点仅是该点为极值点的必要条件,其充分条件是这点两侧的导数异号.另外,使f′(x)无意义的点也要讨论,因为不可导点也可能是极值点. 错解f′(x)=x3+bx2-(2+a)x+2a,由f′(1)=0,得b=1-a. 所以g′(x)=x3+bx2-(a-1)x-a=x3+(1-a)x2-(a-1)x-a=(x-a)(x2+x+1). 因为x2+x+1>0,所以,当x 所以a-6<2a-3≤a,即-3 故所求a的取值范围为(-3,3]. 剖析上述解法的错误之处是没有充分挖掘题目的隐含条件a≠1,造成扩大a的取值范围的情况.事实上,由f′(1)=0,得b=1-a,此时,f′(x)=x3+(1-a)x2-(2+a)x+2a=(x-1)(x+2)(x-a),当a=1时,f′(x)=(x-1)2(x+2),函数f(x)在x=1处没有极值. 正解f′(x)=x3+bx2-(2+a)x+2a,由f′(1)=0,得b=1-a. 所以f′(x)=x3+(1-a)x2-(2+a)x+2a=(x-1)(x+2)(x-a). 如果a=1,那么x=1就只是使导函数值为0的点而非极值点,故b=1-a且a≠1. g′(x)=x3+bx2-(a-1)x-a=x3+(1-a)x2-(a-1)x-a=(x-a)(x2+x+1). 因为x2+x+1>0,所以,当x 所以a-6<2a-3≤a,即-3 综上可知,a的取值范围为(-3,1)∪(1,3]. 警示研究函数的极值与其导函数的关系时,求出f′(x)的零点后,要判断导函数在零点两侧的函数值符号.若符号相反,则该零点是可导函数f(x)的极值点;若符号相同,则不是极值点.解本题时易忽视a≠1.因此,题目中的隐含条件能否挖掘彻底、利用是否充分,往往是我们成功解题的关键. A.a∈(-∞,-3] B.a=-3 C.a=3 D.a∈(-∞,3] 则a≤-3.故选D. 剖析混淆函数的“单调区间是”与函数“在区间上单调”的区别致误. 警示在解决与函数的单调性有关的问题时要注意下列几个概念的区别:“在区间上单调”指该区间是函数相应单调区间的子区间;“单调区间是”指该区间就是函数的相应最大单调区间;“存在单调区间”指该区间内有相应单调性,也可能有别的单调性,即该区间内可能既有增区间,也有减区间. 错解设g(x)=(2x-x2)ex,则 g′(x)=(2-x2)ex. 剖析上述解法的错误之处是数形结合思想使用中图象失真致错,想当然地认为,在g(x)=(2x-x2)ex中,当x→-∞时,y→+∞,而没有充分验证,犯了思维定式的错误. 正解设g(x)=(2x-x2)ex,则 g′(x)=(2-x2)ex. 当x→-∞时,y→0且x<0时,y=g(x)=(2x-x2)ex<0. 图1 例10正解 除了上述几类典型的易错问题以外,常见的还有忽视函数的定义域、构造原函数不当、错把f′(x0)当成关于x的变量函数、忽视切点在曲线上的隐含条件致错等,由于篇幅所限,在此不作赘述.总之,学习中要认真总结,多加思考,明确易混易错问题的类型,弄清致错根源,防患于未然.6 混淆“导数值的正负”与“函数增减性”的逻辑关系
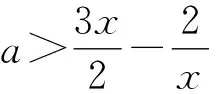
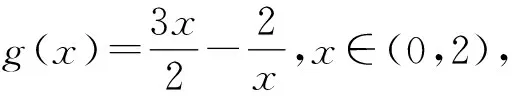
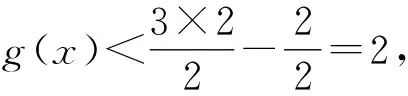
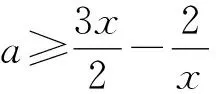
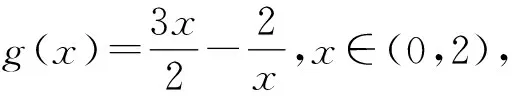
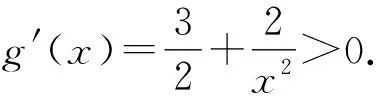
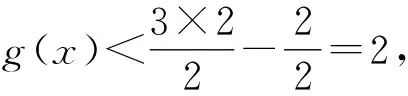
7 误认为函数的极值只能在导数为零的点处取得

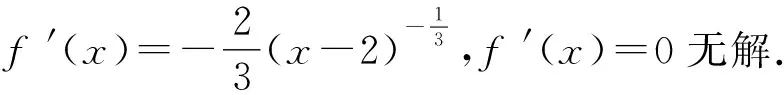
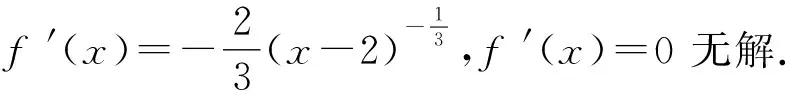
8 隐含条件利用不充分致错
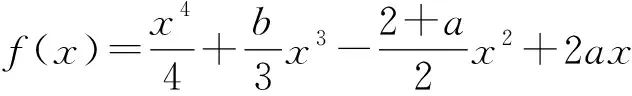
9 混淆函数的“单调区间是”与函数“在区间上单调”致错
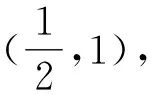
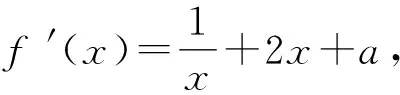
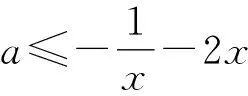
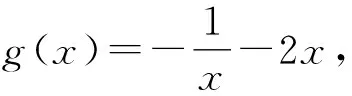
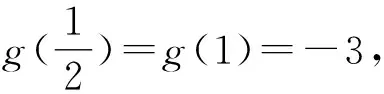
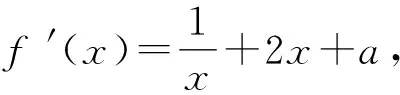
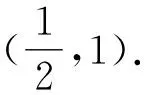
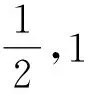
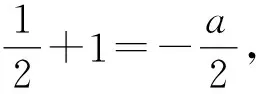
10 数形结合思想使用中图象失真致错
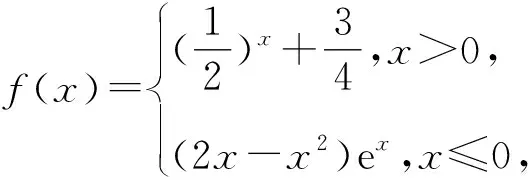
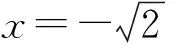
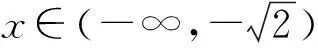
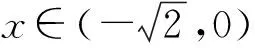
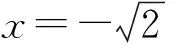
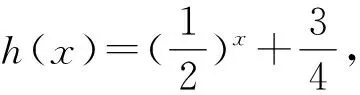
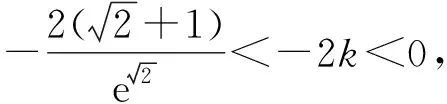
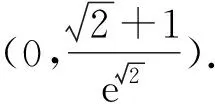
11 结束语

