Abel公式在数学竞赛中的应用
李鸿昌
(北京师范大学贵阳附属中学,贵州 贵阳 550081)
Abel公式本身是一个恒等式,它源自大学的“数学分析”课程,在高等数学中有着广泛的应用. 例如,通过Abel公式,可以证明用来判断级数收敛的Abel判别法和Dirichlet判别法.另外,因为Abel公式只涉及两个实数组,而且方法是初等的,所以学生容易理解并接受[1]. 许多与求和相关的竞赛试题,都有Abel公式背景.若能熟练掌握Abel公式,则可看透问题的本质,迅速解决问题.
1 Abel公式
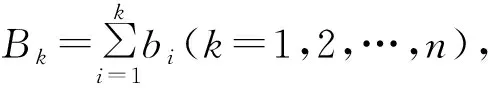
可简记为
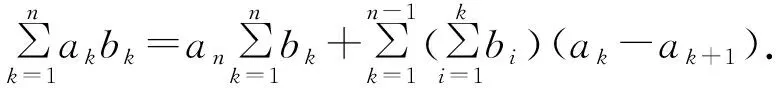
证明因为b1=B1,bn=Bn,bk=Bk-Bk-1(k=2,3,…,n-1),所以(a1-a2)B1+(a2-a3)B2+…+(an-1-an)Bn-1+anBn=B1a1+(B2-B1)a2+…+(Bn-Bn-1)an=a1b1+a2b2+…+anbn.
2 如何使用Abel公式
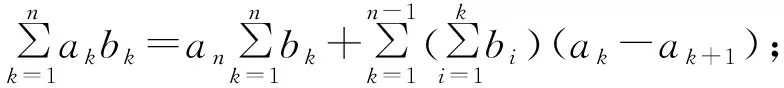
3 Abel公式在竞赛试题中的应用
3.1 在代数不等式中的应用
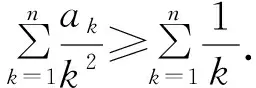
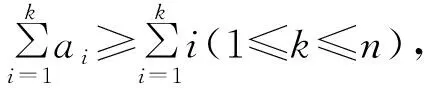
由Abel公式,得
点评上式倒数第二步是逆用Abel公式.
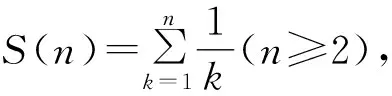
证明由Abel公式,得
=nS(n).
我们将其推广,可得到一般性命题:
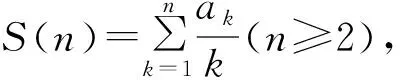
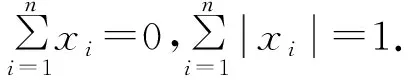
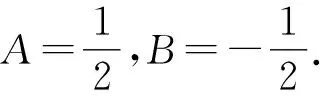
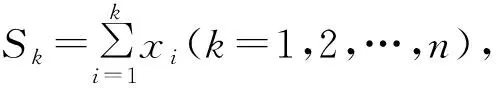
于是,由Abel公式,得
我们将其推广,可得到一般性命题:
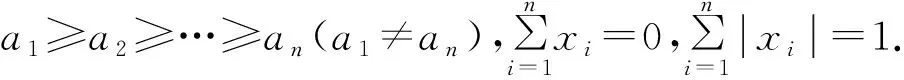

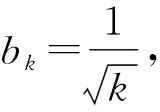
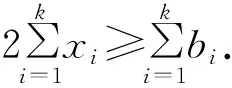
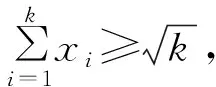
这个不等式显然成立,因为
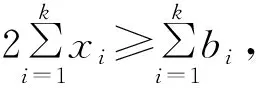
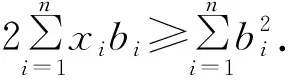

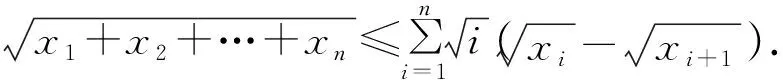
证明由题设,可知
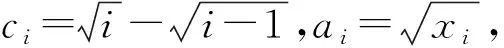

a1c1+a2c2+…+ancn≥a1b1+a2b2+…+anbn.
由均值不等式,对k=1,2,…,n,有
又因为ak≥ak+1(k=1,2,…,n),所以由Abel公式,得
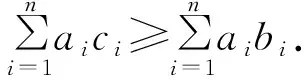
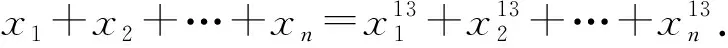
证明由Abel公式,得到
因为y1 应用Abel公式,可得 因此,由Abel公式得 再进一步推广,可得: 当n=1时,结论显然成立. 假设对于1≤k≤n-1,有Ak≤[kx],则由Abel公式,得 所以,由归纳假设及[x]+[y]≤[x+y],有 =n[nx], 故An≤[nx]. Abel公式可导出一系列有价值的命题,而且也为数学奥林匹克的命题提供了理论依据.从上文的案例来看,不难发现有许多的奥林匹克竞赛试题的命题背景均与Abel公式有关. 应用Abel公式,可以较好地解决一些较复杂的、带有约束条件的、涉及数列求和的不等式问题,而这些问题用其他方法是不易解决的.通过学习Abel公式,可让学生熟悉求和符号∑的用法,培养学生的恒等变形能力与数学抽象素养,提高运算效率与解题能力,尤其是解决竞赛中的不等式问题.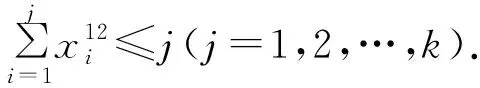
3.2 在三角不等式中的应用
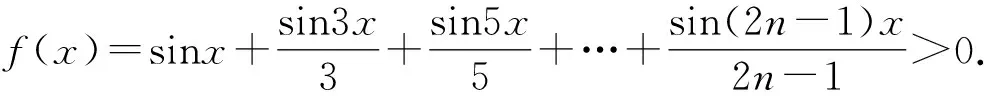
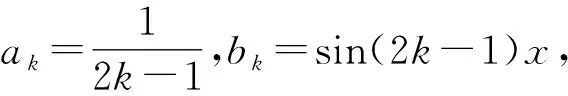
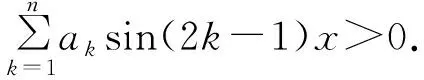
3.3 与数学归纳法结合的妙用
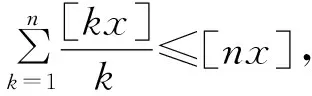
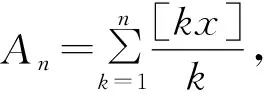
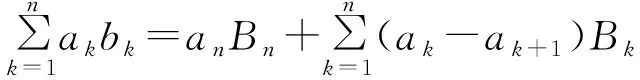
4 结束语

