利用泰勒公式进行编题

马晓娟

(银川市第二中学,宁夏 银川 750001)

泰勒公式的主要作用是用多项式逼近函数和近似计算. 由泰勒公式可以得到诸多的不等式,近几年的高考导数题常以这些不等式为背景,或者利用这些不等式可以快速解决部分高考导数题.

1 泰勒公式

若函数f(x)在点x0存在n阶导数,则有

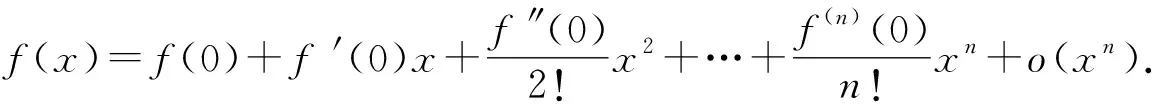
2 常用不等式

由泰勒公式,我们得到以下常用不等式.

(2)对数函数:ln(1+x)≤x.

3 利用泰勒公式编拟试题

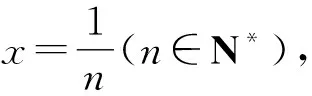
试题1已知函数f(x)=plnx+(p-1)x2+1.

(1)讨论函数f(x)的单调性;

(2)当p=1时,f(x)≤kx恒成立,求实数k的取值范围;

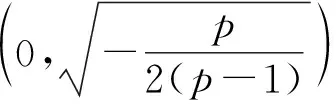
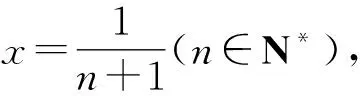
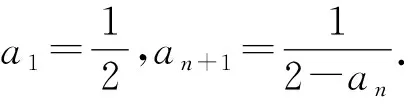
(1)求证:f(x)≤-1;

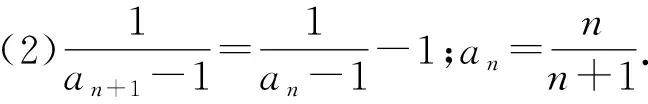
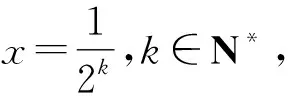
试题3 已知函数f(x)=x-1-alnx.

(1)若f(x)≥0,求a的值;

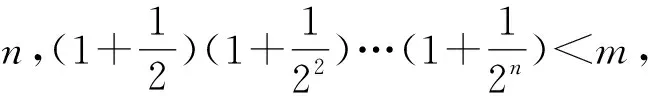
答案(1)a=1;(2)m=3.

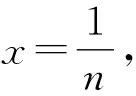
试题4 已知函数f(x)=eax-x-1,其中a>0.

(1)若f(x)≥0恒成立,求a的值;

答案(1)a=1.

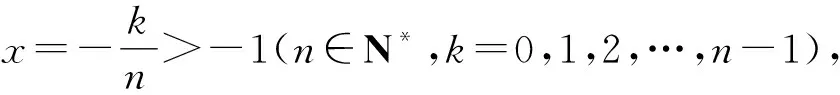
分别取k=n-1,n-2,…,1,0,累加得

试题5 已知函数f(x)=ex-ax-1(a>0,e是自然对数的底数).

(1)求函数f(x)的最小值;

(2)若f(x)≥0对任意的x∈R恒成立,求实数a的值;

答案(1)f(x)的最小值为f(lna)=elna-alna-1=a-alna-1;(2)a=1.

编题6 由泰勒公式,有

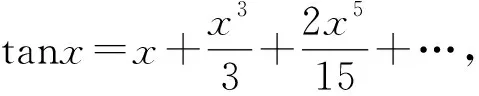
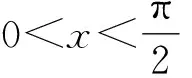
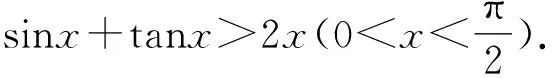
试题6证明:

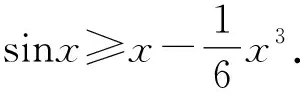
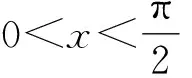
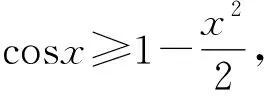
引入参数a,可知当a≥1时eax≥ex,所以此时sinx-cosx≤eax-2恒成立.

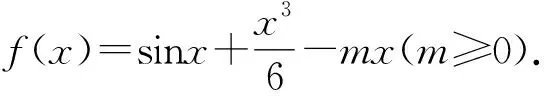
(1)若f(x)在[0,+∞)上单调递增,求实数m的取值范围;

(2)当a≥1时,∀x∈[0,+∞)不等式sinx-cosx≤eax-2是否恒成立?并说明理由.

4 结束语

作为教师,对试题的研究应该有五重境界.境界一,能一题多解;境界二,能多题一解;境界三,能将试题进行变式与推广;境界四,能洞悉试题背景;境界五,能自己编题. 最近几年的高考压轴题都具有高等数学背景[3],这要求一线教师不仅要熟悉一定的高等数学知识,而且还要能将高等数学知识进行初等化处理,然后进行编题.