深度思考探本质 拓展变式提能力

杨媛媛 田万华

(湖北省赤壁市第一中学,湖北 赤壁 437300)

圆锥曲线是代数和几何的交汇,往往是数与形的结合,以及动点与定点的结合问题.特别是在定点、定值问题中有很好的体现.而且,很多试题背后都隐藏着一般性结论.在教学中,教师需要深度思考问题本质,变式拓展提高学生的能力.

1 试题呈现

(1)求椭圆E的标准方程;

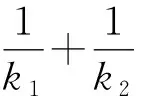
2 试题解析

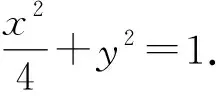
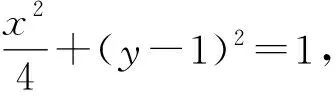
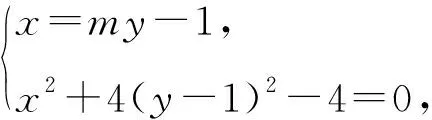
(m2+4)y2-(2m+8)y+1=0.

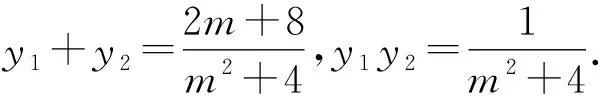
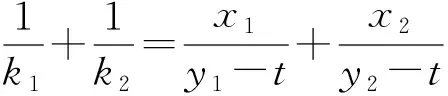
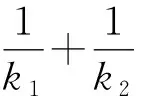
3 拓展探究

思考1 本题中本质上为两个定点、一个定值问题,是否隐藏着某种定点或定值的模型.结合本题定点T(0,-1)恰好是椭圆的下顶点,因此,笔者首先提出以下问题:

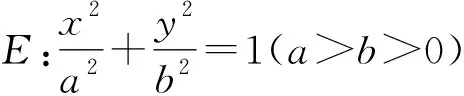
因为b2x2+a2y2-a2b2=0,

所以b2x2+a2(y+b)2-2a2b(y+b)=0.

所以b2x2+a2(y+b)2-2a2b(y+b)·[mx+n(y+b)]=0.

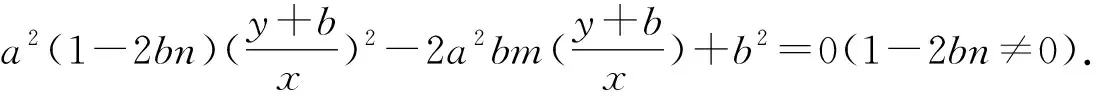
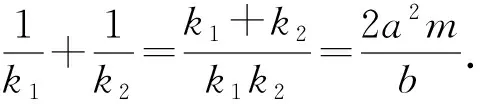
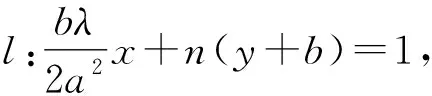
当换成其他顶点时,同理可证直线l过定点,因此得到以下性质:

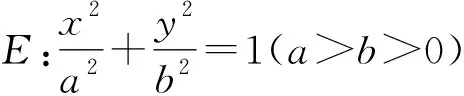
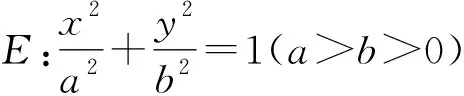
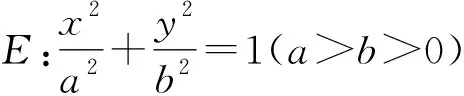
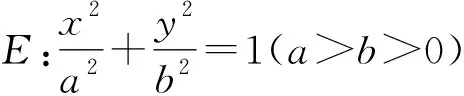
思考2 通过以上的探究,当定点取椭圆的顶点时,模型中的直线均过定点.如果定点取椭圆上的任意一点时,模型中的直线是否也过定点?因此,笔者提出以下问题:

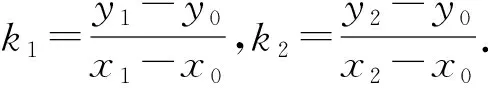
所以b2(x-x0)2+a2(y-y0)2+2b2x0(x-x0)+2a2y0(y-y0)=0.所以b2(x-x0)2+a2(y-y0)2+2b2x0(x-x0)[m(x-x0)+n(y-y0)]+2a2y0(y-y0)[m(x-x0)+n(y-y0)]=0.

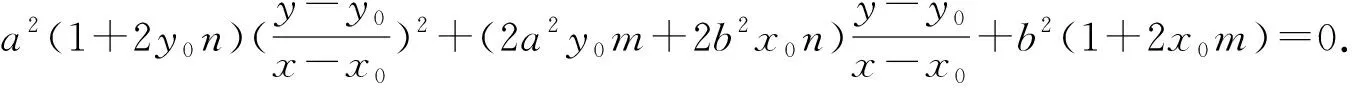
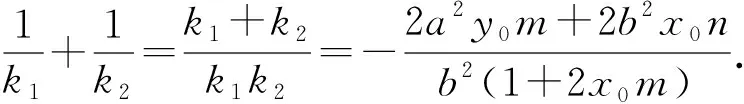
所以2m[b2x0(x-x0)-b2λx0(y-y0)-a2y0(y-y0)]=b2λ(y-y0)+2b2x0.

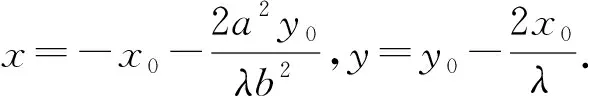
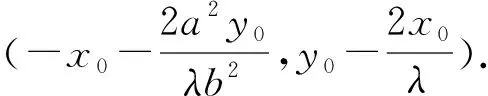
前文中的四条性质是它的特殊情况,由于此一般性结论的形式比较复杂,求解的计算量也较大,所以试题常结合前四条性质进行考查[1].

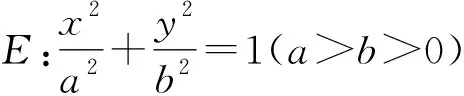
4 试题变式

基于上述性质,可将2023届武汉市九月调研考试21题做如下变式进行考查,也可结合双曲线、抛物线进行类似的考查.

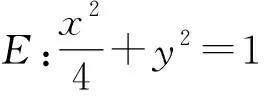
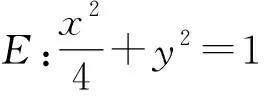
5 结束语

“掌握数学本质,启发思考,改进教学”是高中数学课程的基本理念.教学过程中,面对各式各样的试题,教师要善于展开解题探究和归纳总结,通过问题探究、拓展变式加深学生对数学知识的理解,形成良好的认知结构,促进模型的构建和方法的掌握.这样的教学过程,不仅有利于促进学生迁移能力的形成和发展,还有利于发散性思维能力的培养和提高.