一道联考题的解法探讨和拓展研究

黄尚鹏

(湖北省监利市实验高级中学,湖北 监利 433300)

图1 例题图

(1)小球对斜面的压力大小;

(2)水平面对斜面的支持力大小;

(3)斜面体的加速度大小;

1 对原题的分析与解答

首先判断系统在水平恒力F的作用下小球没有脱离斜面.

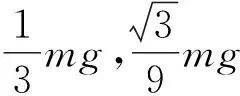
如图2所示,设斜面的加速度为a′,水平向右为正方向,小球相对斜面的加速度为a相,沿斜面向上为正方向.

图2 斜面与小球加速度方向

方法一根据小球和斜面在垂直于斜面方向的加速度分量相等求解

方法二用加速度矢量图求解

如图3所示,画加速度矢量图,根据绝对加速度=相对加速度+牵连加速度,得小球的加速度a0=a相+a′,再对小球的加速度沿水平方向和竖直方向正交分解,得a0=ax+ay

图3 加速度矢量图 图4 小球受力分析图

根据加速度矢量图,由几何关系,得

①

对斜面受力分析,由牛顿第二定律,得

②

对小球受力分析如图4所示,沿水平方向和竖直方向正交分解,由牛顿第二定律,得

沿水平方向:

③

沿竖直方向:

④

联立①②③④,解得

方法三用非惯性系和惯性力求解

如图5所示,小球的加速度是a相和a′的合成,沿水平方向和竖直方向正交分解,得

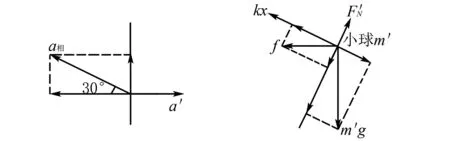
图5 小球加速度正交分解 图6 小球受力分析图

以向左为正方向,小球的水平方向加速度为

ax=a相cos30°-a′

①

以向上为正方向,小球的竖直方向加速度为

ay=a相sin30°

②

系统在水平方向合外力为零,由牛顿第二定律,得

③

在斜面参照系(非惯性系)中研究小球的运动,在非惯性系中应用牛顿第二定律研究物体的运动时,物体除受真实力作用外还受惯性力作用,对小球受力分析如图6所示,惯性力f的方向与斜面的加速度a′的方向相反,惯性力f的大小为

f=m′a′

④

对小球沿斜面方向,由牛顿第二定律,得

⑤

垂直于斜面方向,由平衡条件,得

⑥

联立①②③④⑤⑥解得

小球的加速度大小为

显然,以上三种解法得出的答案完全相同!

点评本题是2021年12月湖北省荆州市六县市高三联考的一道选择题,原选择题中命题者加了一个附加条件:撤去力F的瞬间,假设斜面对小球的支持力不变.通过本文的分析与解答可知这个附加条件是错误的,故原题具有科学性错误,导致没有正确选项,但本题去掉这个附加条件后虽然可以求解,但难度很大.在本文给出的三种解法中,严格来说,只有方法一是高考范围内的解法,方法二和方法三是竞赛解法,因此本题对原题改编后是一道非常不错的竞赛题.方法一巧妙抓住“小球和斜面在垂直于斜面方向的加速度分量相等”这一特征求解,属于特殊快捷解法,要求考生要有敏锐的洞察力,一般考生难以想到;方法二巧妙利用加速度矢量图建立小球的加速度分量和斜面的加速度之间的关系,增加了方程个数,从而使问题顺利解决,属于竞赛中的常规解法;方法三巧妙选斜面为参照系,灵活运用相对运动加速度合成规律,并在非惯性系中引入惯性力求解,属于高观点解法.虽然用非惯性的观点能使某些复杂的动力学问题简化,从而可以比较圆满地解决一些问题,但要特别注意,在非惯性系中引入的惯性力与真实力不同,惯性力不是物体与物体间的相互作用,它没有施力物体,因而也没有反作用力,惯性力是为了解决问题的方便而人为地引入的假想的力.

2 对原题的拓展研究

拓展在撤去力F后,试求t时刻弹簧的伸长量x(t)和斜面体向右的加速度a′(t).

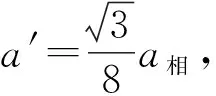
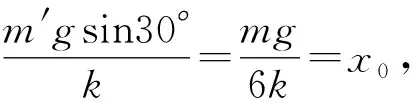
再令X=x-x0,X即为偏离平衡位置的位移(注意:a相与X方向相反)

小球相对斜面的振动方程为

故t时刻弹簧的伸长量

⑦

斜面体向右的加速度

⑧

由⑦可知,弹簧的原长位置是小球振动的最大负位移处,故弹簧一直处于伸长状态[1].

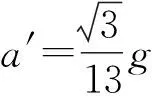
点评拓展部分我们巧妙选斜面(非惯性系)为参照系,论证得出小球相对斜面做简谐运动,从而使问题顺利解决.简谐运动是一种很重要的物理模型,在中学物理竞赛中有极其广泛的应用.建立简谐运动模型,我们不但可以计算振动的周期或频率,而且还可以求解物体的运动规律.

3 结束语

综上,运用“建立简谐运动模型求解物体的运动规律” 这一重要方法解决问题的关键是论证物体做简谐运动,解决问题的基础是确定物体振动的平衡位置、振幅和角频率并能根据初始条件正确书写振动方程[2].运用这种方法不仅丰富了处理物理问题的手段,拓展了我们的思维,还为高中阶段的后续学习奠定了思维基础.因此,对于参加物理竞赛的学生,应当深刻领会这一方法并能熟练应用.