三角形的解析性质与运用

傅建民

(陕西咸阳渭城中学,陕西 咸阳 712000)

解三角形是大家非常熟悉的问题,常用正弦定理与余弦定理.本文试图从代数的角度来理解三角形,得到了三角形的解析性质,从而为解三角形开辟了新的途径.

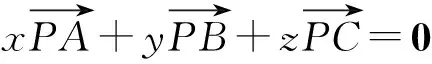
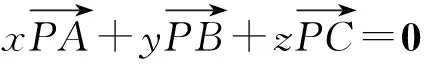
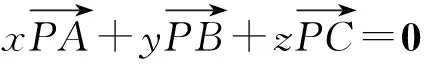
1 点的向量坐标

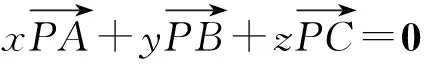
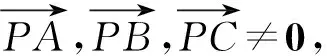
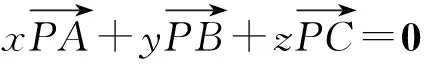
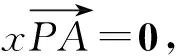
同理x′,y′,z′中至多一个为0,因此三对数x与x′,y与y′,z与z′当中至少有一对均非零,不妨设z与z′均非零,则存在一个非零常数k0∈R,使得k0z=z′.

我们知道点P不可能同时在三角形的三条边所在的直线上,所以我们不妨假设点P不在边AB所在的直线上.

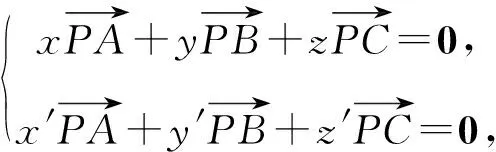
两式相减,得

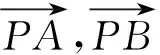
所以k0x-x′=0,k0y-y′=0.

即k0x=x′,k0y=y′.

又k0z=z′,故(x,y,z)与(x′,y′,z′)为同类解.这与假设(x,y,z)与(x′,y′,z′)是不同类解矛盾.

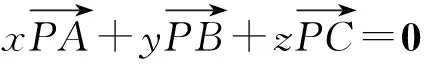
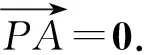
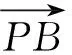
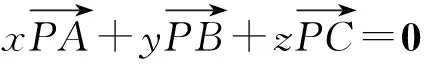
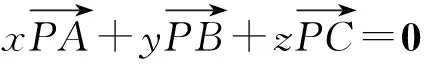
首先我们证明其中的x+y+z≠0.

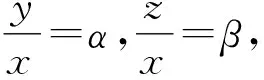
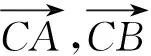
设A(x1,y1),B(x2,y2),C(x3,y3),O为原点,则

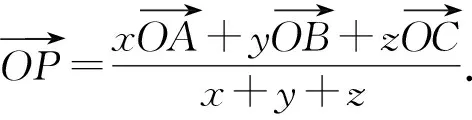
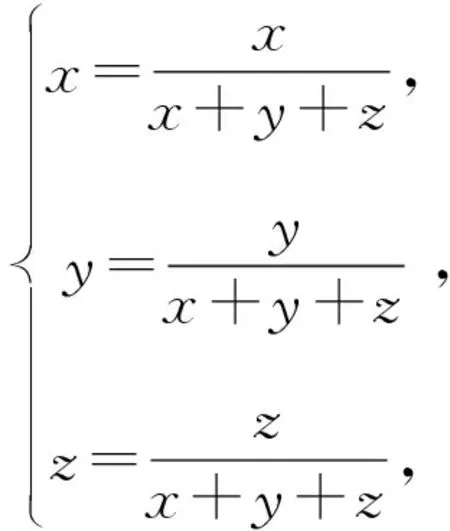
故点P坐标是(xx1+yx2+zx3,xy1+yy2+zy3).

若点P在直线l:Ax+By+C=0上,

则A(xx1+yx2+zx3)+B(xy1+yy2+zy3)+C=0.

又x+y+z=1,

所以x(Ax1+By1+C)+y(Ax2+By2+C)+z(Ax3+By3+C)=0.

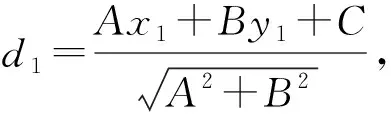
则xd1+yd2+zd3=0

即xd1+yd2+zd3=0.

由此我们得到下面结论:

注d1,d2,d3可正、可负、可零,在l同侧取同号,异侧取异号.

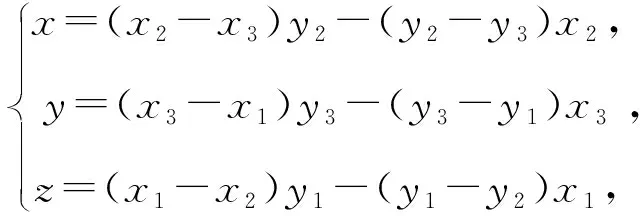
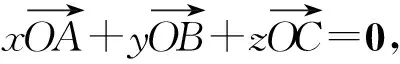
注当x=0时,点O在直线BC上;当y=0时,点O在直线CA上;当z=0时,点O在直线AB上.因为点O不可能同时在直线BC,CA,AB上,所以x,y,z不全为0.

现在的问题是:其中的x,y,z是否具有几何意义呢?

我们知道直线BC的方程是:(x2-x3)y-(y2-y3)x=(x2-x3)y2-(y2-y3)x2.

点O到直线BC的距离

当点O不在直线BC上时,△BOC的面积

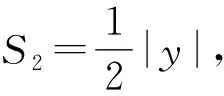
下面我们换一个思路,化简x,y,z,有

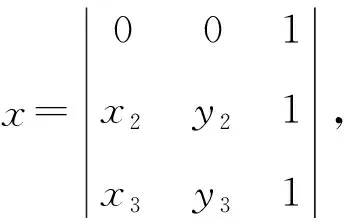
当O→B→C→O为逆时针时,x为正;

当O→C→A→O为逆时针时,y为正;

当O→A→B→O为逆时针时,z为正.

所以当x,y,z同号时,点O位于△ABC的内部,反之亦然.

此时当A→B→C→A为逆时针时,x,y,z同正;当A→B→C→A为顺时针时,x,y,z同负.

当x,y,z不同号时,点O位于△ABC的外部,反之亦然.

同时有:|x|∶|y|∶|z|=S1∶S2∶S3.

其中S1,S2,S3分别是△BOC,△AOC,△AOB的面积.

于是我们有结论:

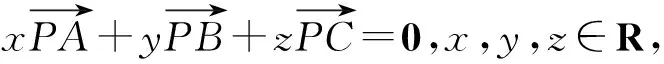
有了前面的预备知识,我们容易得到下面结论:

定理2 设点I,O,O*,H,G分别为△ABC的内心、外心、与边BC相切的旁心、垂心(不与点A,B,C重合)、重心,则

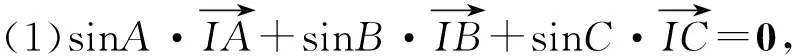
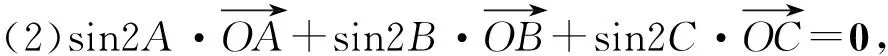
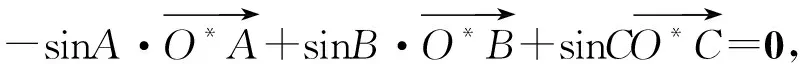
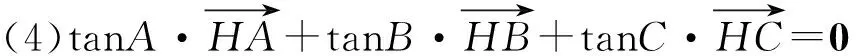
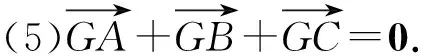
2 重要结论

结合定理1的推论1与定理2,我们得到结论:

设点I,O,O*,H,G分别为△ABC的内心、外心、与边BC相切的旁心、垂心(不与点A,B,C重合)、重心,顶点A,B,C到直线l的距离分别为|d1|,|d2|,|d3|.

(1)若内心I在直线l上,则d1sinA+d2sinB+d3sinC=0,反之亦然;

(2)若外心O在直线l上,则d1sin2A+d2sin2B+d3sin2C=0,反之亦然;

(3)若旁心O*在直线l上,则-d1sinA+d2sinB+d3sinC=0,反之亦然;

(4)若垂心H在直线l上,则d1tanA+d2tanB+d3tanC=0,反之亦然,此时△ABC是非直角三角形;

(5)若重心G在直线l上,则d1+d2+d3=0,反之亦然.

注d1,d2,d3可正、可负、可零,在l同侧取同号,异侧取异号.

3 应用

例1(2020届河北省石家庄市第二中学高三下学期教学质量检测数学试题第16题)在平面直角坐标系下,三角形的三个顶点分别为A(1,0),B(0,2),C(m,n),位于动直线l:y=k(x-1)的两侧,其中一侧有一个点,点到直线l的距离记为d1,另一侧有两个点,两个点到直线l的距离之和记为d2.若无论直线怎么变化,总有d1=d2,则m+n=____.

解析因为无论直线l怎么变化,总有d1=d2,根据上述结论(5),我们知道直线l恒过△ABC的重心,又动直线l:y=k(x-1)恒过定点(1, 0),故△ABC的重心为定点(1, 0).

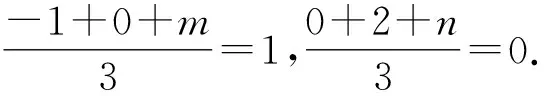
解得m=4,n=-2.

所以m+n=2.

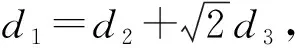
解析根据三角形的顶点坐标,我们知道△ABC是等腰直角三角形.

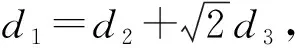
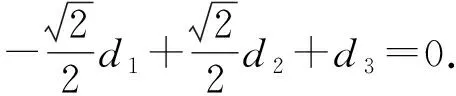
所以-d1sinA+d2sinB+d3sinC=0.

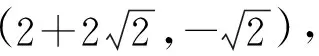
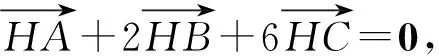
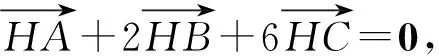
因为点H是△ABC的垂心,所以

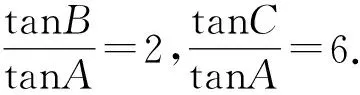
由tan(B+C)=-tanA,得

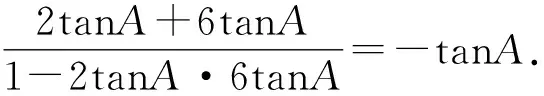
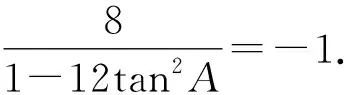
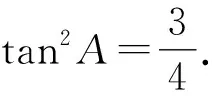
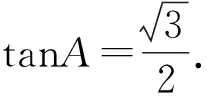
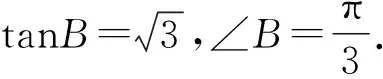
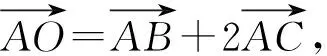
解析假设∠ABC是直角,则外心O是AC的中点.

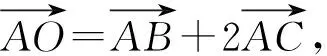
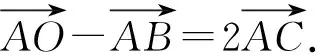
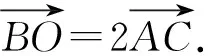
所以三点A,B,C共线,这与题设矛盾.

所以∠ABC非直角,故sin2B≠0.

因为点O为△ABC的外心,

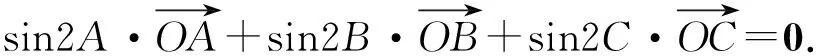
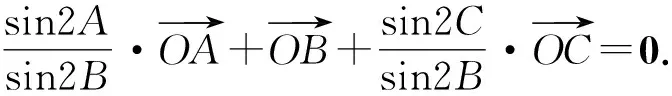
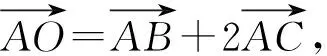
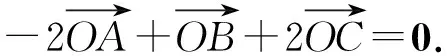
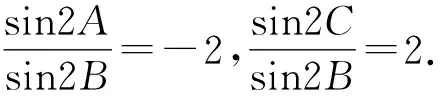
从而有sin2A=-sin2C.

解得2A-2C=π或2C-2A=π.

当2A-2C=π时,2B=2π-(2A+2C)=2π-[(π+2C)+2C]=π-4C,

因为sin2C=2sin2B=2sin(π-4C)=2sin4C,

所以sin2C=4sin2Ccos2C.

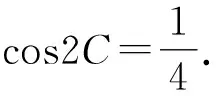
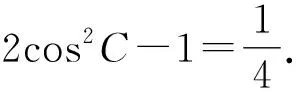
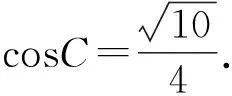
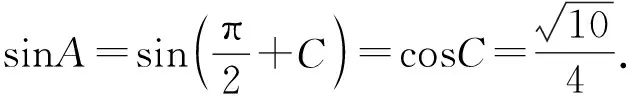
当2C-2A=π时,2B=2π-(2A+2C)=2π-[(2C-π)+2C]=3π-4C,

因为sin2C=2sin2B=2sin(3π-4C)=2sin4C,

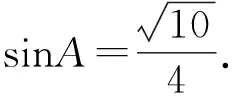
4 结束语

对于几何问题,张景中先生基于点几何提出两种思路[1]:思路一就是将一个个点求出来,再考虑几何关系,与解析法相比,无需将点转化为坐标,只需求出点与点之间的关系,这样一来,点几何计算相对简明,几何意义也更明确;思路二就是表示出已知与结论,并建立恒等式以揭示已知和结论之间的关系.