探究圆锥曲线中的一类斜率之和问题

高继浩

(四川省名山中学,四川 雅安 625100)

圆锥曲线含有丰富的性质,近年来,各类定点、定线、定值问题频频出现在高考、大型模考等各类考试题中,其中很多试题背后都隐藏着深刻的背景.圆锥曲线定值问题中,十分常见的一类便是斜率定值问题,本文对一道圆锥曲线斜率定值问题进行多次推广,并类比到双曲线和抛物线中,最后给出对偶变式,有利于我们看清问题的本质.

1 试题呈现

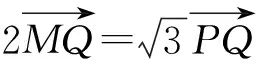
(1)求动点M的轨迹方程E;

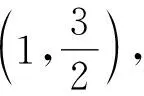
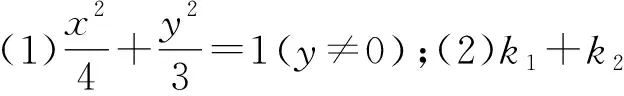
2 推广探究

将试题第(2)问进行一般化推广得到:

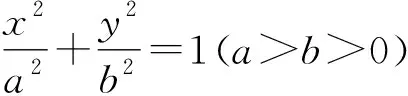
若点N不在椭圆上,k1+k2还是定值吗?于是将命题1进一步推广为:

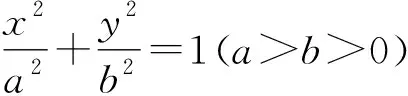
若点N的横坐标不为c,还有相应的定值吗?于是得到:

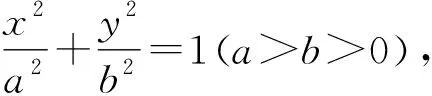
证明若直线AB的斜率为0,则

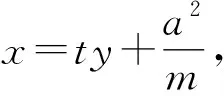
设A(x1,y1),B(x2,y2),则

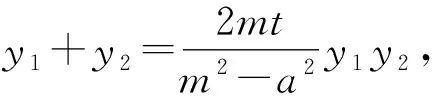
综上,命题得证.

3 类比探究

将命题3引申到双曲线中,得到:

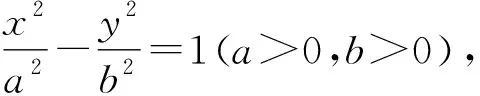
命题4的证明与命题3类似,略.

类比到抛物线中,得到:

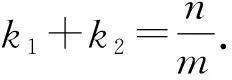
证明显然直线AB的斜率不为0,设其方程为x=ty-m,与抛物线方程联立,消去x得

y2-2pty+2pm=0.

设A(x1,y1),B(x2,y2),则

y1+y2=2pt,y1y2=2pm.

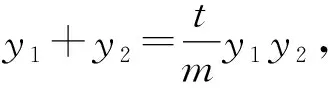
4 对偶探究

受文[1][2]启发,将命题3、命题4中点T的位置改为在y轴上[1-2],得到:

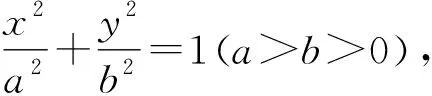
证明若直线AB的斜率不存在,则

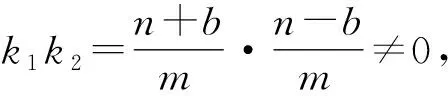
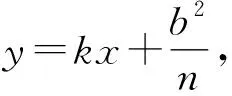
设A(x1,y1),B(x2,y2),则

即a2b2k2+(n2-b2)(a2k2+b2)>0,且

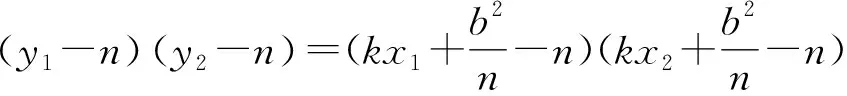
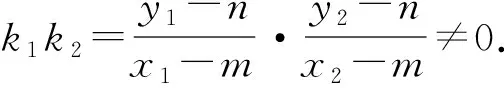
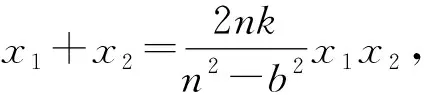
综上,命题得证.

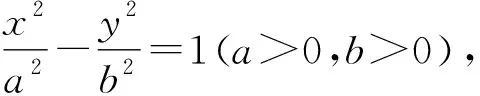
命题7的证明与命题6类似,略.

5 结束语

在平时的教学中,我们应该对圆锥曲线中的典型问题进行探究、拓展、变式,实现对一类问题的深度学习,达到触类旁通的效果.