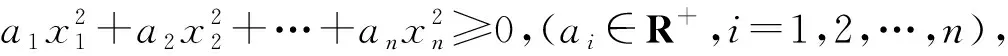从代数恒等式到代数不等式

胡 坚

(江苏省淮安市金湖县第二中学,江苏 淮安 211600)

1 从代数恒等式到常用不等式

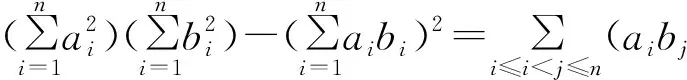
点评这就是从拉格朗日(Lagrange)恒等式到柯西(Cauchy)不等式.

例2 设a,b>0,由a3+b3-ab(a+b)=(a+b)(a-b)2,得到a3+b3≥a2b+ab2.

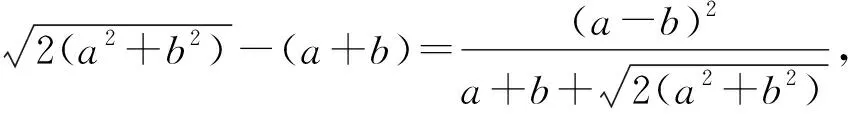
点评这就是不等式2(a2+b2)≥(a+b)2,用此不等式可以速解2014年浙江考题:

设实数a,b,c满足a+b+c=0,a2+b2+c2=1,则c的最大值是____.

我们还可以将此不等式推广到三次方或者三元、n元的情况.

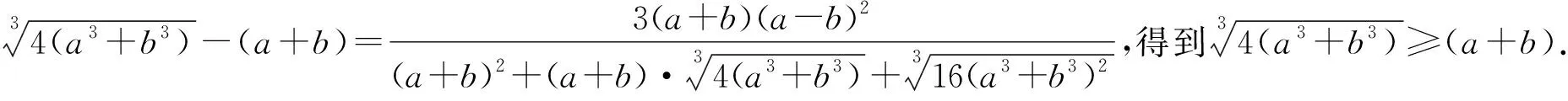
即4(a3+b3)≥(a+b)3.

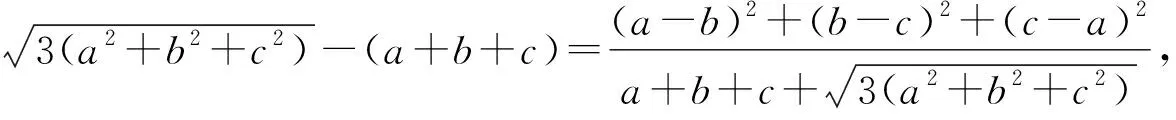
即3(a2+b2+c2)≥(a+b+c)2.

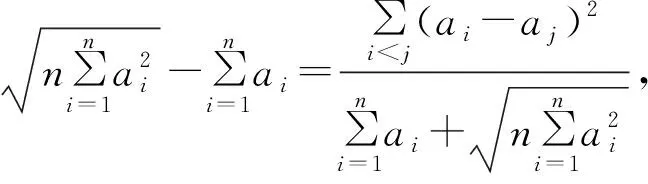
2 从恒等式的角度证明不等式

例7A,B,C为△ABC的内角,求证:对任意的x,y,z,有x2+y2+z2-2xycosC-2yzcosA-2xzcosB≥0.

证明x2+y2+z2-2xycosC-2yzcosA-2xzcosB=(x-ycosC-zcosB)2+(ysinC-zsinB)2,

所以欲证不等式成立.

点评还可以将条件“A,B,C为△ABC的内角”弱化为“A+B+C=(2n+1)π”. 若条件改为“A+B+C=2nπ”,则有x2+y2+z2+2xycosC+2yzcosA+2xzcosB≥0[1].

例9 证明:对任意的正实数x,y,有

证明因为(x2+2yz)[x(y+z)+y2+z2]2-[x2(y+z)+y2(z+x)+z2(x+y)]2=2x(y+z)(y2+z2)+2y4-y3z+2y2z2-yz3+2z4=2x(y+z)(y2+z2)+(y-z)2(y2+yz+z2)+(y2+z2)2>0,

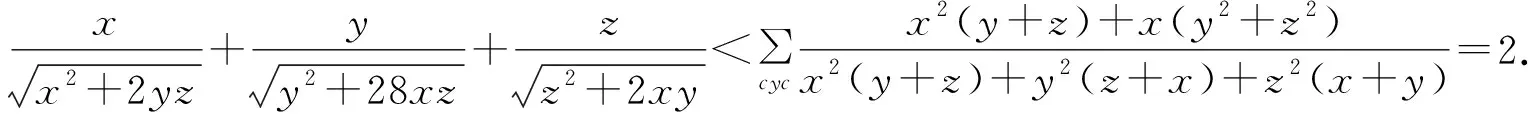
例10 (2017年清华大学自主招生试题)已知实数x,y满足5x2-y2-4xy=5,则2x2+y2的最小值是____.

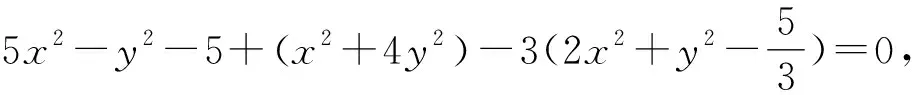
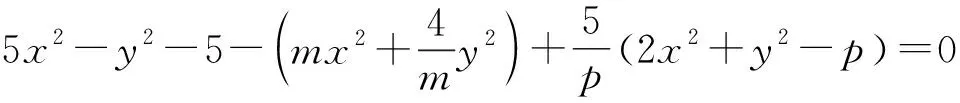
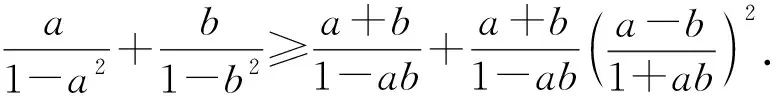
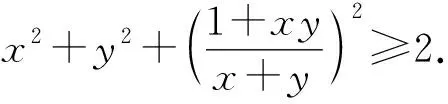
例13已知正数x,y,z,证明:x2+xy2+xyz2≥4xyz-4.

所以x2+xy2+xyz2≥4xyz-4.

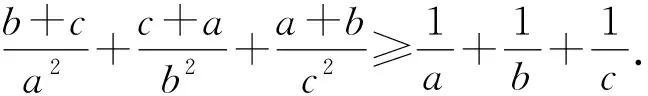
=(a3b2+a2b3+b3c2+b2c3+a3c2+a2c3-a2b2c-a2bc2-ab2c2)/(a2b2c2),

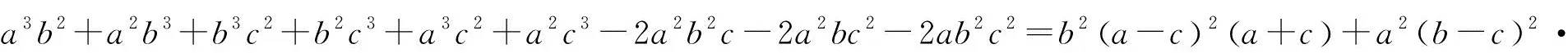
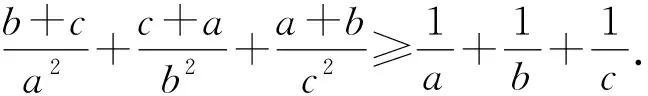
例15 已知a,b,c,d∈R+,abcd=1,求证:

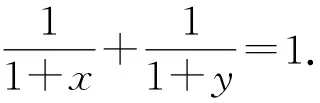
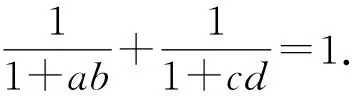
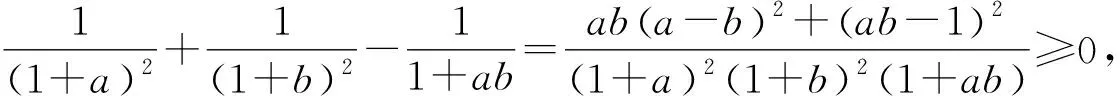
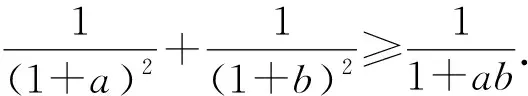
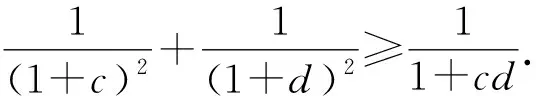
两式相加可知原不等式得证[2].

3 SOS定理的介绍

在前文,笔者提到,可以把欲证不等式化为

这就是平方和(SOS)方法的基本思想.

SOS定理考虑表达式S=f(a,b,c)=Sc(a-b)2+Sb(c-a)2+Sa(b-a)2,其中Sa,Sb,Sc是关于变量a,b,c的表达式,则如果下列条件中至少有一个成立,那么不等式S≥0成立.

(1)Sa≥0,Sb≥0,Sc≥0;

(2)a≥b≥c且Sb≥0,Sb+Sa≥0,Sb+Sc≥0;

(3)a≥b≥c且Sa≥0,Sc≥0,Sa+2Sb≥0,Sc+2Sb≥0;

(4)a≥b≥c且Sb≥0,Sc≥0,a2Sb+b2Sa≥0;

(5)a≥b≥c是某三角形的三条边,且Sa≥0,Sb≥0,b2Sb+c2Sc≥0;

(6)Sa+Sb+Sc≥0且SaSb+SbSc+ScSa≥0

4 结束语