泰勒公式在高考数学中的应用探索
鲁 灏
(深圳中学,广东 深圳 518001)
泰勒公式是高等数学中的一个重要知识内容,其中心思想是将x=x0处具有n阶导数的函数f(x)近似为一个x-x0的n阶多项式函数.通过泰勒多项式,我们可以将指数函数、对数函数、三角函数等与初等函数联系起来,了解函数在x0的某邻域内的各类性质[1].
近年的高考试题中也频繁出现具有高等数学知识背景的试题,因此在高中数学命题、解题的过程中,探讨泰勒公式等高等数学知识的应用,可以帮助教师打开命题思路,优化解题方法,拓展学生视野.
1 泰勒级数
若函数f(x)在区间D上有定义,且n+1阶导数存在,x,x0∈D,则有:
(a)
这里Rn(x-x0)n为拉格朗日余项.如果在(a)式中去掉Rn(x-x0)n,那么在x0附近f(x)可用(a)式右边的多项式来近似代替.如果函数f(x)在x=x0处存在任意阶的导数,我们称下列形式的级数为函数f(x)在x0处的泰勒级数:
(b)
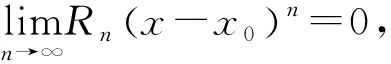
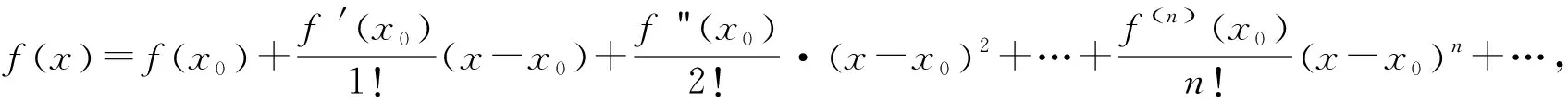
(c)
特别地,如果x0=0,(c)式可以写成下面形式,称为麦克劳林级数:
通过上述定理,我们可以得到许多常用函数在x=0处的泰勒展开式:

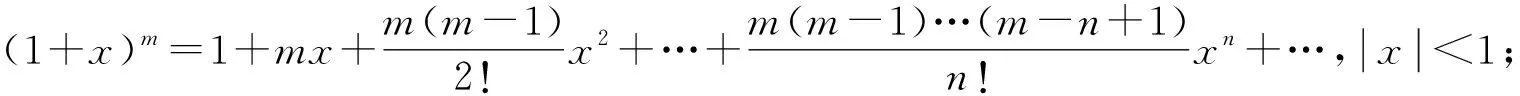
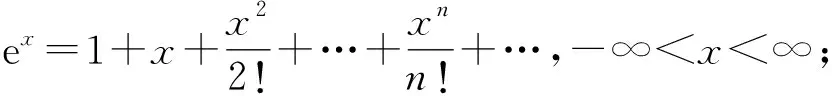
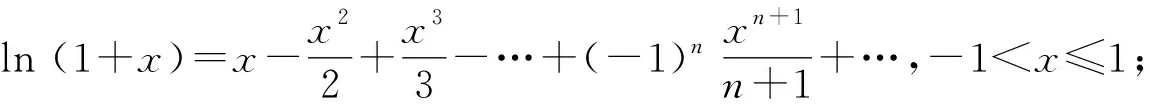
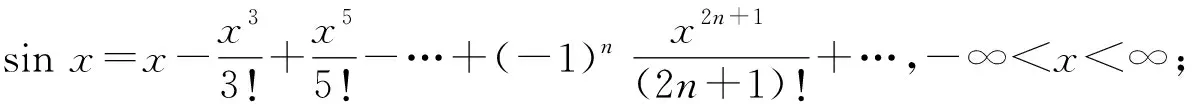
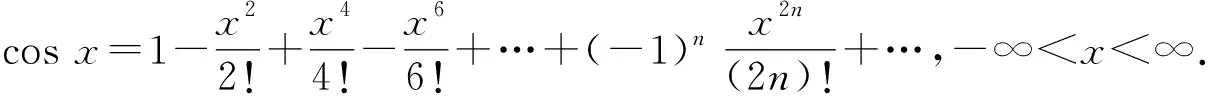
在使用泰勒展开式时需要注意函数是否存在任意阶导数,还需要注意泰勒级数的收敛区间.基于①-⑥式,可以通过变量代换、四则运算或逐项求导、逐项求积等方法,间接地求得其他函数的幂级数展开形式.如:

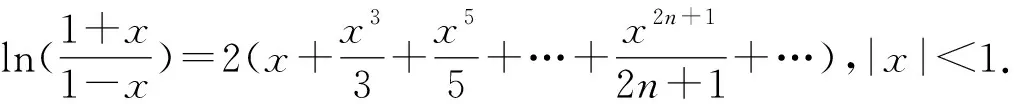
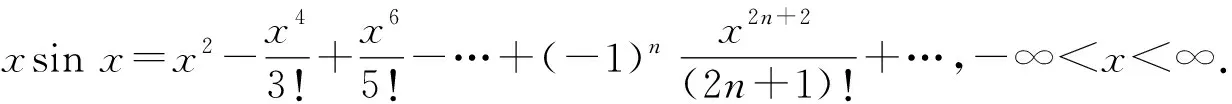
2 高考中泰勒公式的应用
2.1 比较函数值大小
在近年的高考试题中,比较数值大小的选择题较多.常规的解法是构造函数,通过讨论函数的单调性解题,但耗费的时间往往较多,这一类题目如果利用泰勒公式就能迎刃而解.
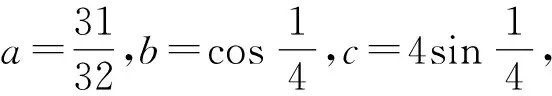
A.c>b>aB.b>a>c
C.a>b>cD.a>c>b
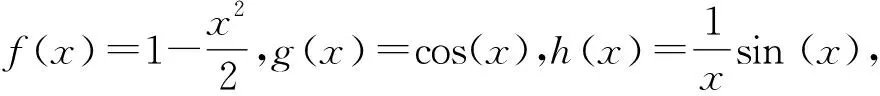
将函数g(x)与h(x)在x=0处展开:
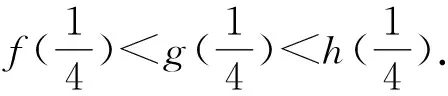
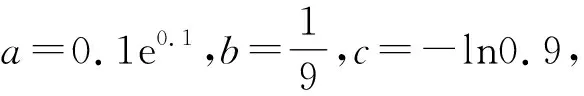
A.a C.c 将函数f(x),g(x)与h(x)在x=0处展开: 易得h(0.1) 类似地,由⑤⑥式,x>0时,可得: A.a C.b 解析由a=2ln(1.01)=ln(1.020 1)>ln(1.02)=b,可知答案为选项B或C,需比较a与c大小.利用②式、④式构造的不等式,可得: 即0.019 9≤a≤0.019 906; 即0.019 8≤c≤0.019 804. 同样可以得到a>c. 例4(2023年新课标Ⅱ卷第22题) (1)证明:当0 (2)已知函数f(x)=cos(ax)-ln (1-x2),若x=0是f(x)的极大值点,求a的取值范围. f′(x)=(2-a2)x+R3(x)3, 计算f′(0)=(2-a2)0+R3(0)3=0. 本文利用泰勒展开式,展现了泰勒函数在处理比较大小、构造不等式、分析函数局部性质这一类题目的高效性.简化了计算过程,也为编制、解答此类题目提供了新的思路.高考的命题成员往往有大学教师,因此,其命题往往是从高等数学的角度出发编制题目.高中数学教师在日常教学中也应多从“高观点”视角出发,联系高等数学与中学数学,注重题目背后蕴含的数学知识的本质.
2.2 构造不等式
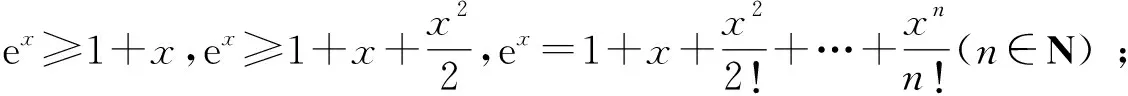
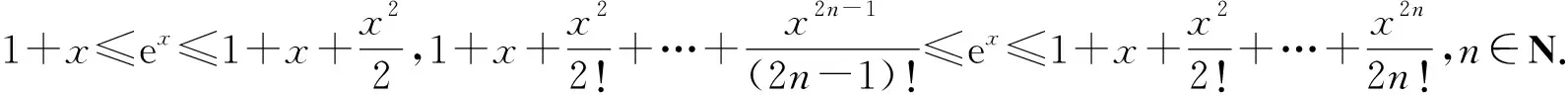
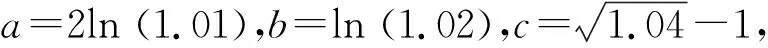
2.3 分析函数的局部性质
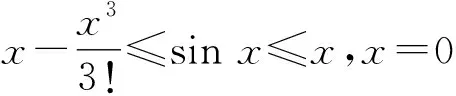
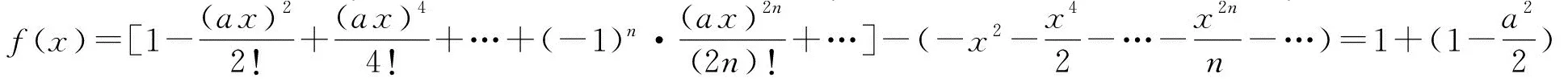
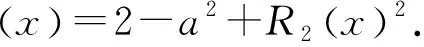

3 结束语

