多视角证明2022年全国甲卷不等式试题
董 强
(西安市第八十五中学,陕西 西安 710061)
高考数学中的最后一道解答题是选修4-5“不等式选讲”的内容,一般难度不大,属于和“极坐标与参数方程”试题二选一的选做题,多考查不等式的证明和求值,主要涉及基本不等式、柯西不等式等.
1 试题呈现
试题(2022年全国甲卷第23题)已知a,b,c均为正数,且a2+b2+4c2=3.
证明:(1)a+b+2c≤3;
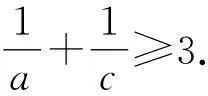
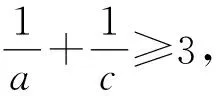
2 试题解析
2.1 第(1)问解析
视角1 构造柯西不等式或基本不等式.
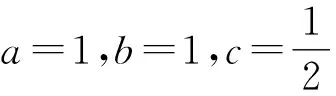
证法2(构造基本不等式)
因为a2+b2+4c2=3,所以6=a2+b2+4c2+3=(a2+1)+(b2+1)+(4c2+1)≥2a+2b+4c.
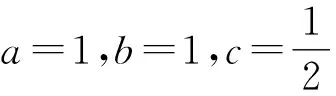
点睛柯西不等式是证明三元及以上不等式的首选方法,巧妙配凑柯西不等式的形式是证明的基础.基本不等式在证明不等式时需要特别注意取等号的条件,尤其是多次使用基本不等式后等号成立的条件应为多个等号成立的共同要求.
视角2利用分析法或作差比较法.
证法3(分析法)因为a,b,c均为正数,且a2+b2+4c2=3,所以要证a+b+2c≤3,只需要证(a+b+2c)2≤9.
即证a2+b2+4c2+2ab+4bc+4ac≤9.
亦即2ab+4bc+4ac≤6.
故只要证2ab+4bc+4ac≤2a2+2b2+8c2.
此式等价于(a-b)2+(a-2c)2+(b-2c)2≥0,上式显然成立,因此,a+b+2c≤3成立.
证法4(作差法)因为a,b,c均为正数,且a2+b2+4c2=3,所以3(a2+b2+4c2)-(a+b+2c)2=2a2+2b2+8c2-2ab-4ac-4bc=(a-b)2+(a-2c)2+(b-2c)2≥0.
结合条件并移项,得(a+b+2c)2≤9.
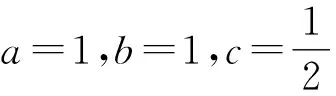
点睛对一些不等式证明的试题,如果正面证明思路不明显,可以考虑利用分析法从待证结论出发,逐步寻求使得结论成立的充分条件,这样逆向思考和倒推,往往会找到证明的突破口.有了分析法的基础,其实就可以巧妙地利用已知条件通过作差法证明不等式了.
2.2 第(2)问解析
视角1构造函数,利用函数单调性.
证法1(直接化归与转化)
因为a2+b2+4c2=3,b=2c,
所以a2+8c2=3.
又因为a>0,
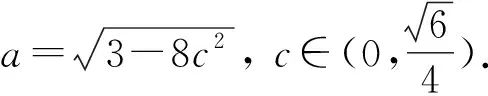

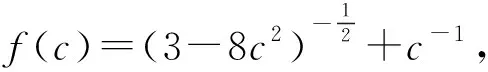
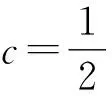
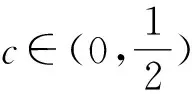
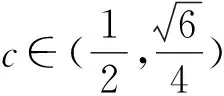
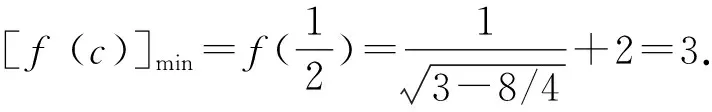
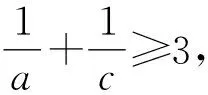
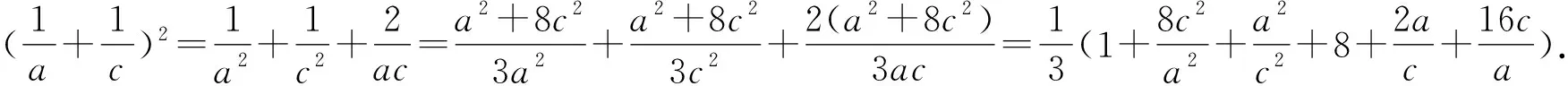
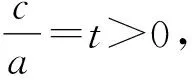
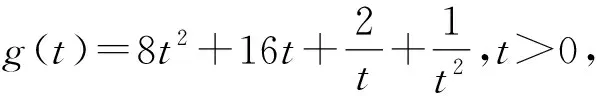
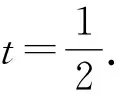
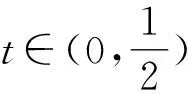
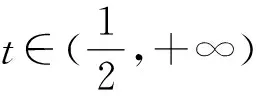
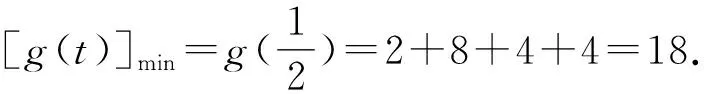
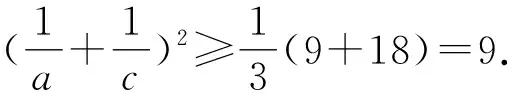
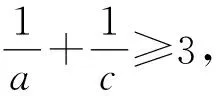
点睛在证明不等式的过程中,如遇到构造定值不方便,基本不等式或柯西不等式的形式等不容易配凑,则可以考虑化归与转化,将问题转化为一元函数问题,利用导数研究所构造函数的单调性,最终实现不等式的证明.
视角2 三角换元,利用赫尔德不等式或权方和不等式.
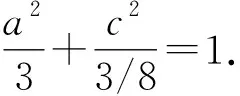
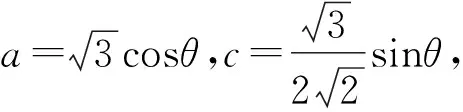
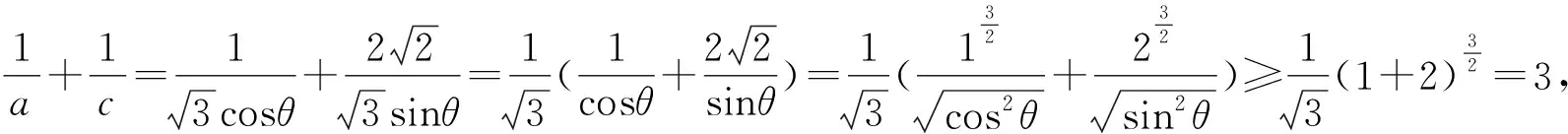
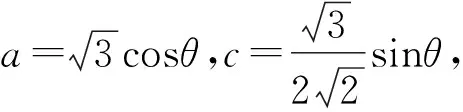
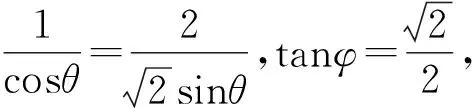
视角3巧妙构造,利用基本不等式.
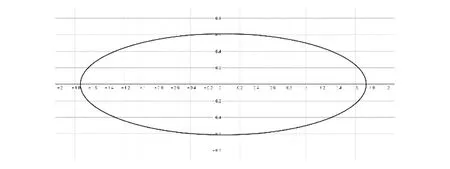
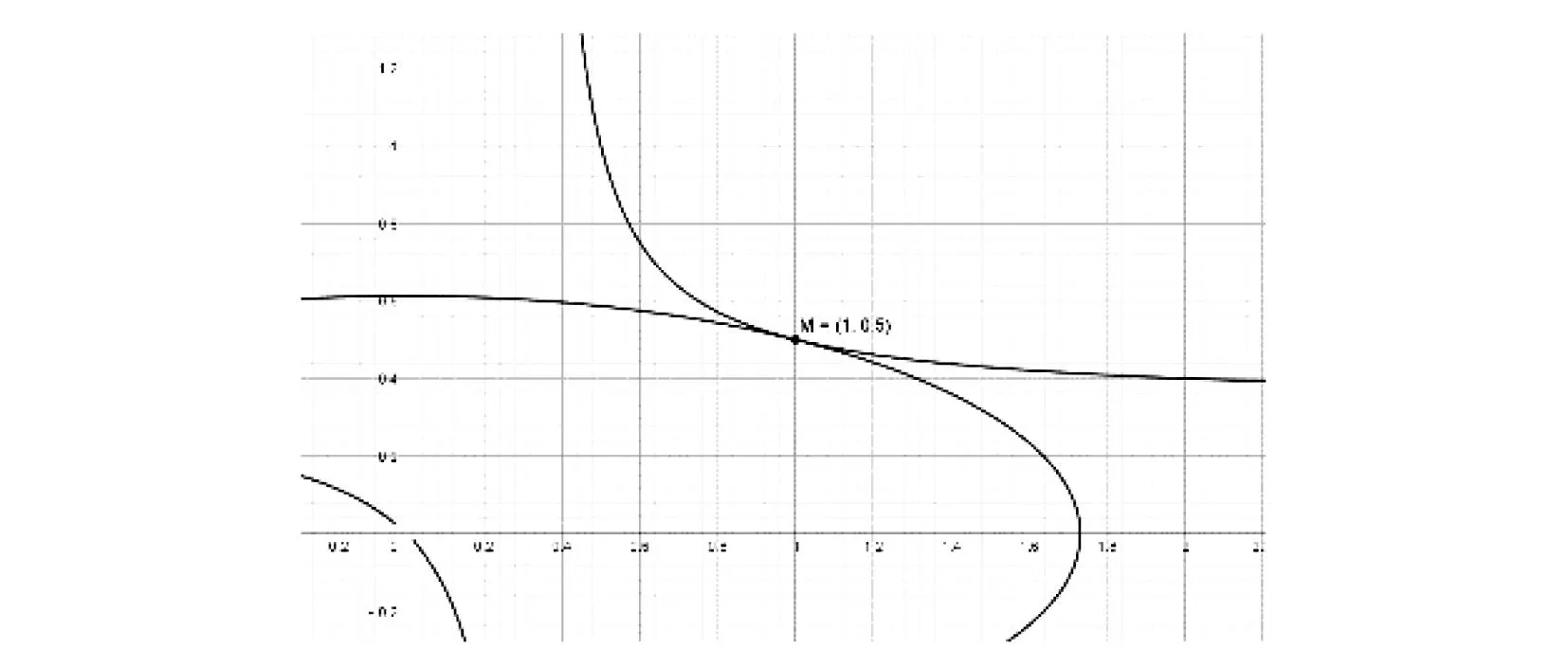
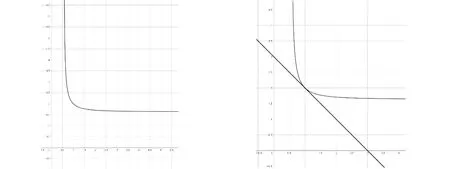
证法5(二元基本不等式)由(1)知a+b+2c≤3,因为a,b,c均为正数,b=2c,所以0 视角4 数形结合,充分利用信息技术. 图1 借用椭圆求最值 图2 取等号时的情形 图3 曲线在第一象限的图象 图4 取最小值时的情形 令z=x+y,则y=-x+z,z是直线系y=-x+z在y轴上的截距.由线性规划知识易知,当直线y=-x+z经过曲线拐点(1,2)时,z取得最小值3. 信息技术可以将复杂问题简单化,抽象问题形象化.通过Geogebra、几何画板等工具能快速画出一些曲线所表示的图形,结合图形,利用代数式表达的几何意义及线性规划等知识,可以实现对问题的简化处理.需要指出的是,信息技术在求具体数值的时候可能存在读数的误差,这与理论证明还是存在一定的差别,不过信息技术能为问题解决提供一条积极的思路[3].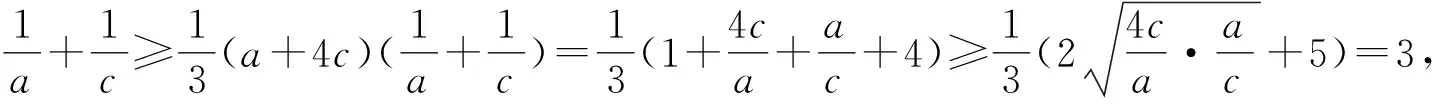
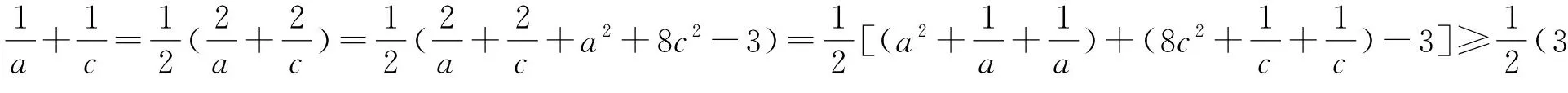
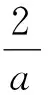
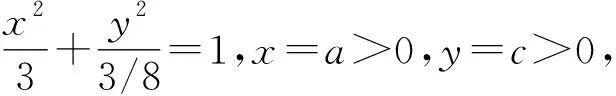
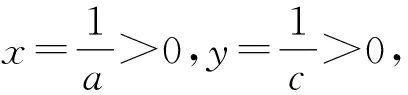
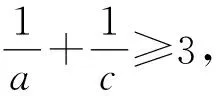
3 结束语

