一道2022年高中数学联赛题的深入探究

王东海

(安徽省肥东县城关中学,安徽 合肥 231600)

在竞赛解题教学活动中,教师不应局限于对题目的具体解答和低水平重复训练,而应引导学生对问题进行深层次的探究及引申,充分挖掘题目的内涵和外延,使学生能够用更高的观点去看待问题.

1 试题呈现

题目(2022年新疆赛区高中数学联赛10题)如图1,已知△ABC内接于抛物线E:x2=y,且边AB,AC所在的直线分别与抛物线M:y2=4x相切,F为抛物线M的焦点.

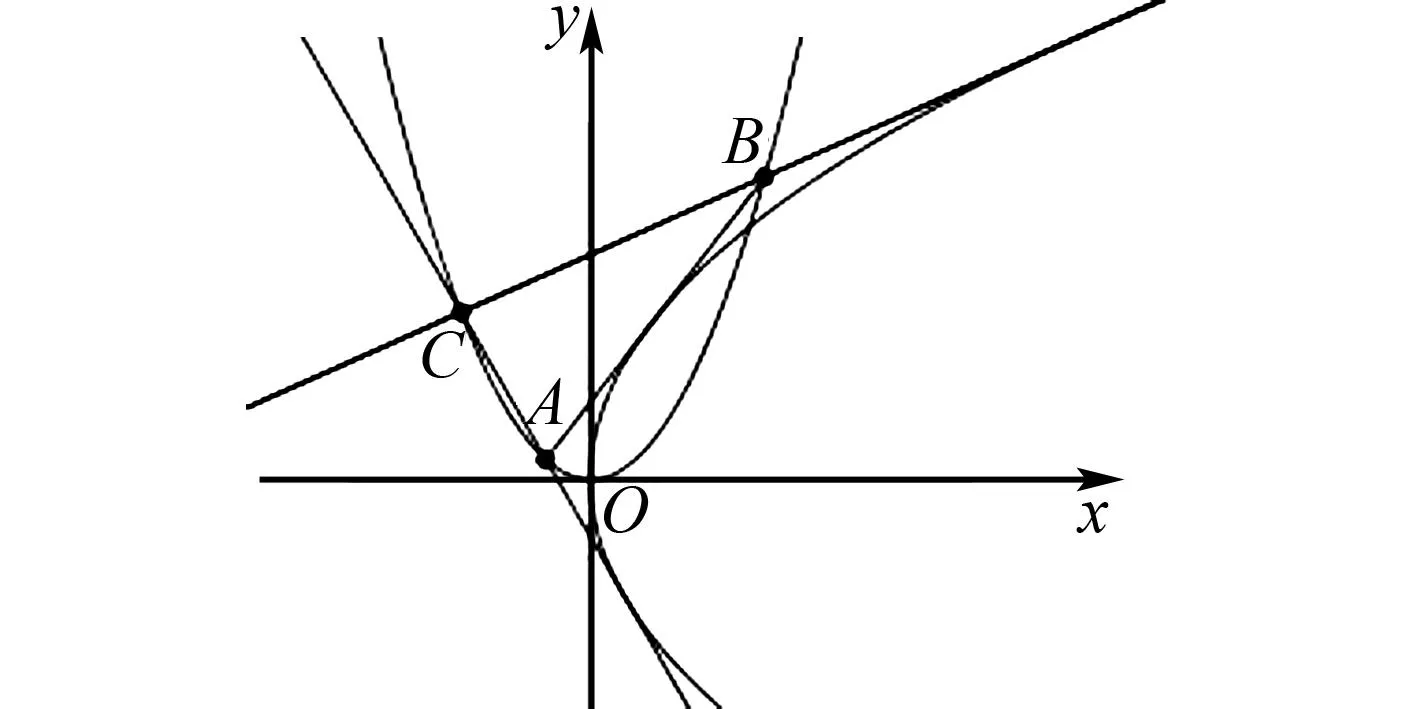
图1 2022年新疆赛区高中数学联赛10题

求证:边BC所在直线与抛物线M相切.

分析与圆锥曲线的切线有关的问题,是近年来数学联赛和高考中圆锥曲线部分比较常见的一类题型,其实质还是考查直线与圆锥曲线的位置关系,只是条件比较特殊,形式比较新颖,解法更加多样.我们可以采取多种方法来处理相切问题.

2 解法探究

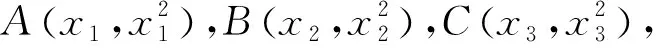
即(x1+x2)x-y-x1x2=0.

代入y2=4x并整理,得

(x1+x2)y2-4y-4x1x2=0.

因直线AB与y2=4x相切,故

△=16+16x1x2(x1+x2)=0.

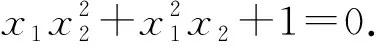
①

同理由直线AC与y2=4x相切,得

②

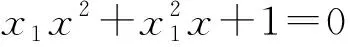
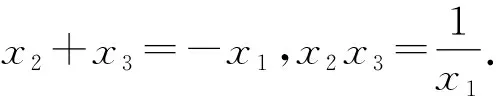
同理直线BC方程与y2=4x联立可得

(x2+x3)y2-4y-4x2x3=0.

所以△=16+16x2x3(x2+x3)

所以BC与抛物线M:y2=4x相切.

解析2前面解题步骤同解析1,由直线AB,AC与y2=4x相切,可得

①

②

①-②式,得

x1(x2-x3)-(x3-x2)·(x2+x3)=0.

又根据题意知B,C的横坐标不相同,即x2≠x3, 从而得x2+x3=-x1.

又①×x3-②×x2,得

(x3-x2)+x1x2x3(x2-x3)=0.

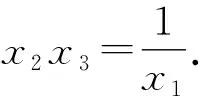
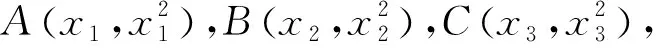
从而由切线的斜率构建等式

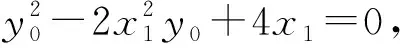
③

④

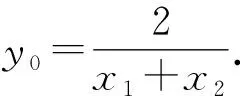
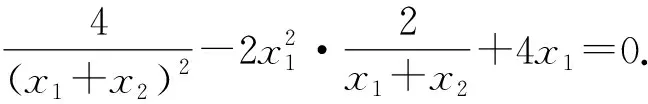
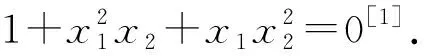
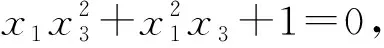
3 推广探究

波利亚曾说:“没有任何一个题目是彻底完成了的,总还会有些事情可以做[2].”细品解题过程和结论,笔者发现解答结论耐人寻味,值得探究.于是笔者思考,对于y2=4x结论成立,那么对于一般性y2=2px是否成立?如果x2=y变为一般性的x2=2py呢?另外,背景的圆锥曲线换成椭圆、双曲线、圆,是否仍有类似的结论呢?基于以上思考,笔者探究得到如下结论.

结论1 已知△ABC内接于抛物线E:x2=y,且边AB,AC所在的直线分别与抛物线M:y2=2px相切,则边BC所在直线与抛物线M也相切.

结论2 已知△ABC内接于抛物线E:x2=2p1y,且边AB,AC所在的直线分别与抛物线M:y2=2p2x相切,则BC所在直线与抛物线M也相切.(结论1是结论2的特殊情况,仅证结论2)

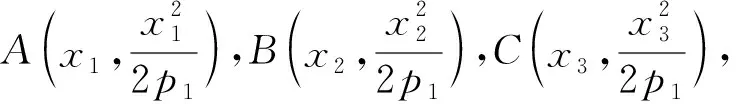
(x1+x2)x-2p1y-x1x2=0.

联立抛物线y2=2p2x消去x,得

(x1+x2)y2-4p1p2y-2p2x1x2=0.

因直线AB与M:y2=2p2x相切,故

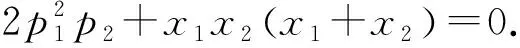
⑤

同理由直线AC与y2=2p2x相切可得

⑥

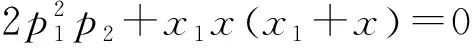
又直线BC方程为(x3+x2)x-2p1y-x3x2=0,代入y2=2p2x,得

(x3+x2)y2-4p1p2y-2p2x3x2=0.

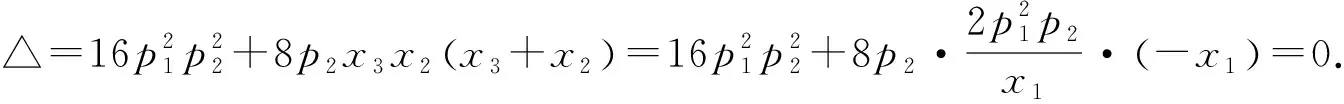
所以直线BC与抛物线M也相切.

若进一步将M:y2=2p2x变为更一般的y2=2p2(x+x0),另外,再将本题中的两条抛物线推广到两个椭圆、两条双曲线、两个圆,那么本题结论是否仍然成立呢?考虑到运算量的关系,这里不再一一推导,感兴趣的读者可用GGB软件进行探讨.综合考虑运算量以及高考和数学联赛中出现的频繁程度,我们选取一个圆锥曲线和一个圆进行探究,即能否找到内接于圆锥曲线且外切于圆的三角形?

如果,这里圆锥曲线选择抛物线y2=2px(p>0),那么抛物线内的所有圆是否都具有该性质?显然当抛物线上的三个点固定时,则它的内切圆是唯一的,只要改变圆的圆心和半径,以上性质将不复存在.也就是说,满足预想结论的圆的圆心与半径是有一定的制约关系的.为了便与计算,我们考虑动圆圆心在x轴上的情形,经过探究与证明得到以下结论:

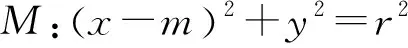
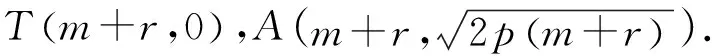
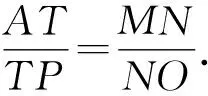
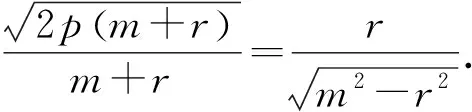
整理,得r2+2pr-2pm=0,

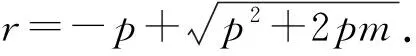
下证一般性:

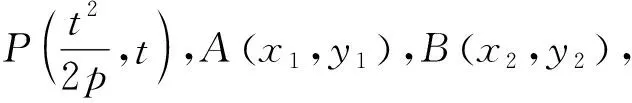
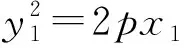
2px-(y1+t)y+ty1=0.

再由直线PA与圆M相切,得

化简,得(t2-r2)x1+(4mpt-2r2t)y1+4m2t2-4p2r2-t2r2=0.

⑦

同理,直线PB与⊙M相切得

(t2-r2)x1+(4mpt-2r2t)y2+4m2t2-4p2r2-t2r2=0.

⑧

从而点A,B在直线(t2-r2)x+(4mpt-2r2t)y+4m2t2-4p2r2-t2r2=0上.

即为AB的方程.此时点M到直线AB的距离

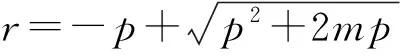
故AB与⊙M相切.

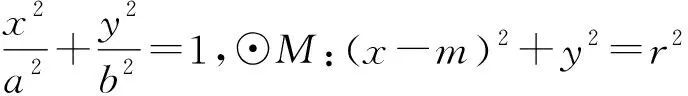
证明先证特殊情况,如图3,当点P与椭圆左顶点重合时,根据对称性知AB⊥x轴,垂足为点T,设PA与圆M相切的切点为N,从而MN⊥PA.

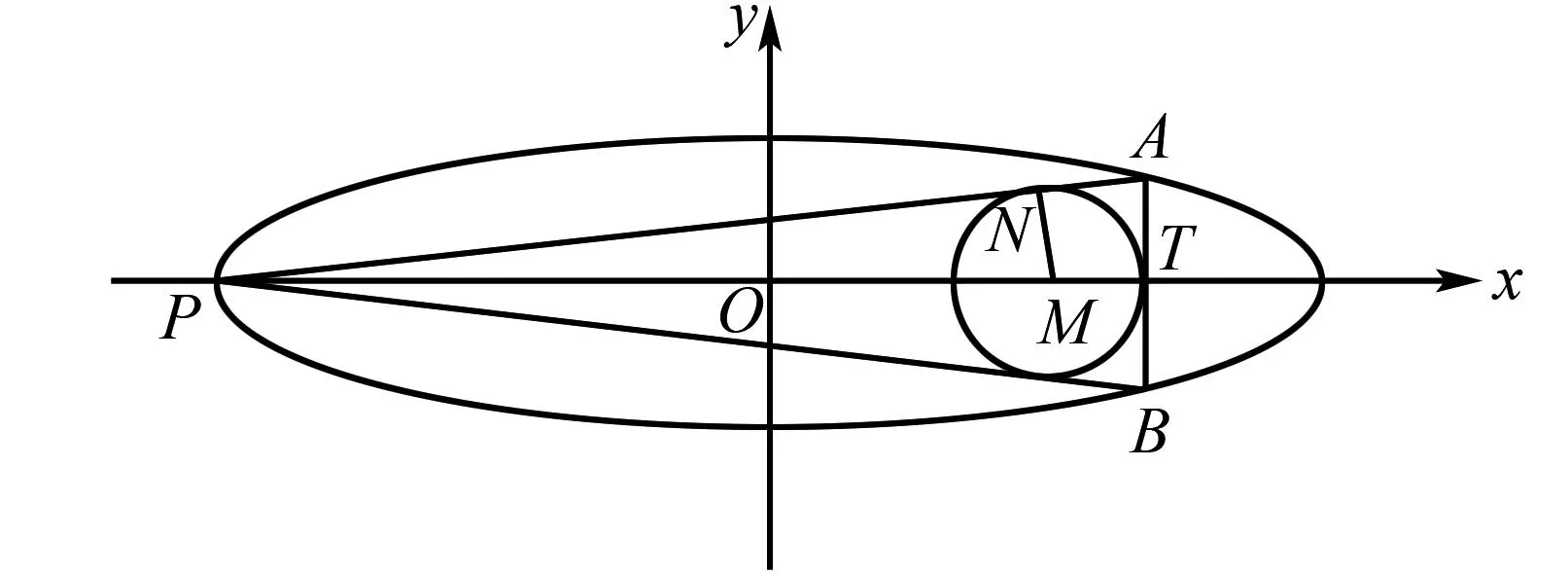
图3 结论4解析图

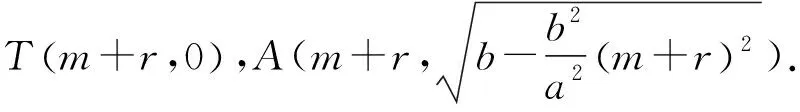
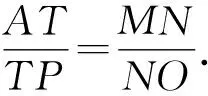
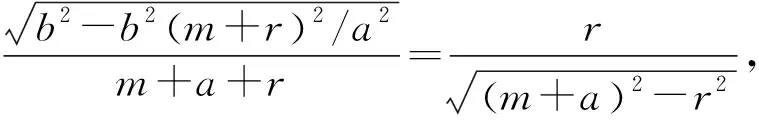
两边平方并去分母可解得

对于一般性的证明,其方法与结论3抛物线相同,但计算过程极其冗长,这里略去.

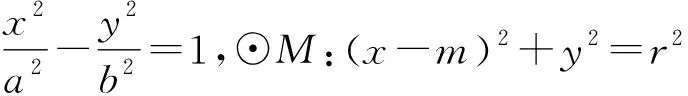
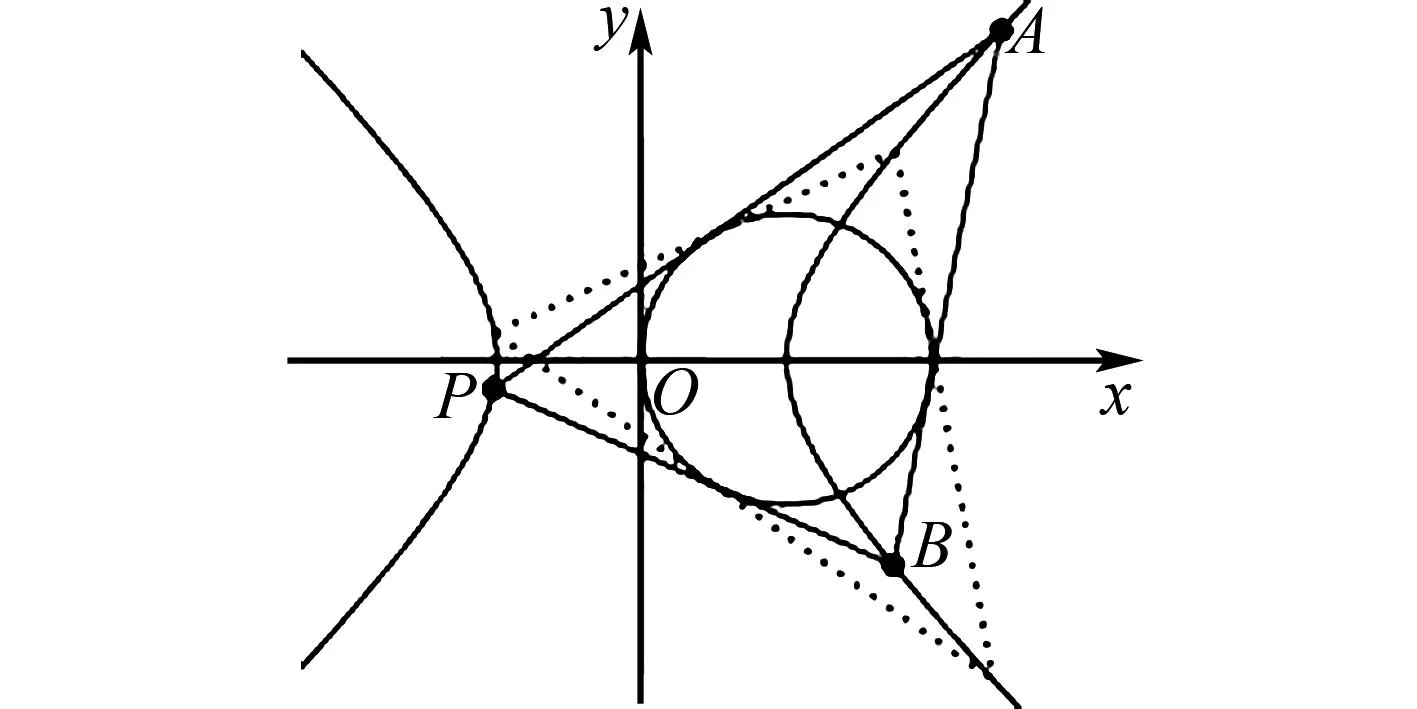
图4 结论5图

4 结束语

这道联赛题中,△ABC外接于抛物线x2=y,又内切于y2=4x,我们把这样的图形结构称为彭赛列闭合.彭赛列闭合定理是1822年法国数学家彭赛列在其出版的著作中给出的,并且给出了严谨的证明.他认为,平面上给定两条圆锥曲线,若存在一封闭多边形外切于其中一条圆锥曲线且内接于另一条圆锥曲线,则此封闭多边形内接的圆锥曲线上每一个点都是满足这样(切、内外接)性质的封闭多边形的顶点,且所有满足此性质的封闭多边形的边数相同.彭赛列闭合定理展示了基于圆锥曲线关系上的一种“群结构”关系——“彭赛列结构”,表示为:有一个满足一种结构的关系存在,则所有满足这种结构的关系都存在.如果从形象化的角度来理解,彭赛列闭合相当于一只跳蚤从外圆锥曲线某点出发,每次沿着向内圆锥曲线作出的一条切线跳到外圆锥曲线上的一个新起点,经过N次跳跃后回到了起点,形成了路径闭合,且跳蚤的路径是否闭合和它的起始位置无关.

另外,本道联赛题考查的内接于抛物线且外切于另一条抛物线的三角形问题,以及拓展中探讨的圆锥曲线的内接三角形的内切圆问题,都是属于“彭赛列闭合定理”的特殊情况.考试中如果提前了解了彭赛列闭合定理,则能为解题指明方向.