谈2023年福建省检第21题的一题多解及拓展延伸

唐 洵

(福建省福清第三中学 ,福建 福清 350000)

题1(福建省2023届高中毕业班适应性练习21)已知圆A1:(x+1)2+y2=16,直线l1过点A2(1,0)且与圆A1交于点B,C,BC中点为D,过A2C中点E且平行于A1D的直线交A1C于点P,记点P的轨迹为Γ.

(1)求Γ的方程;

(2)坐标原点O关于A1,A2的对称点分别为B1,B2,点A1,A2关于直线y=x的对称点分别为C1,C2,过点A1的直线l2与Γ交于点M,N,直线B1M,B2N相交于点Q.请从下列结论中,选择一个正确的结论并给予证明.

①△QB1C1的面积是定值;

②△QB1B2的面积是定值;

③△QC1C2的面积是定值.

1 解法探究

1.1 第(1)问解析

解析(1)作出图形如图1所示,由题意得,A1(-1,0),A2(1,0).

图1 第(1)问解析示意图

因为D为BC中点,

所以A1D⊥BC.

即A1D⊥A2C.

因为PE∥A1D,

所以PE⊥A2C.

因为E为A2C的中点,

所以|PA2|=|PC|.

所以|PA1|+|PA2|=|PA1|+|PC|=|A1C|=4>|A1A2|.

所以点P的轨迹Γ是以A1,A2为焦点的椭圆(左、右顶点除外).

注由于第(1)问较为简单,仅给出参考答案如上;在求解第(2)问之前,先作图2.

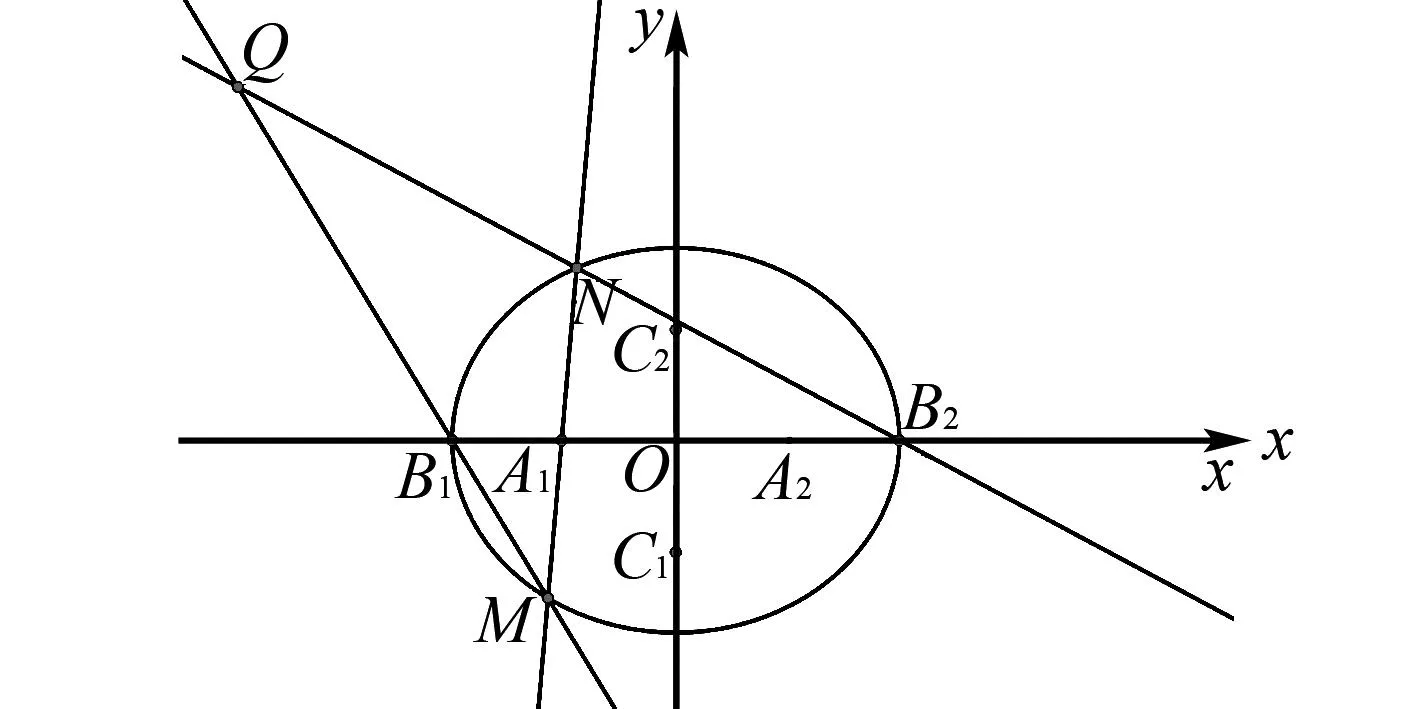
图2 第(2)问示意图

1.2 第(2)问解析

(2)结论③正确;下证:△QC1C2的面积是定值.依题意,B1(-2,0),B2(2,0),C1(0,-1),C2(0,1).

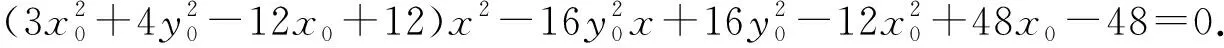
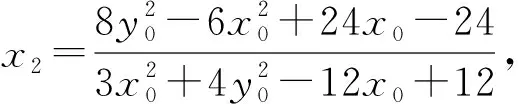
将x1,y1代入上式整理,得

则x0=-4.

故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

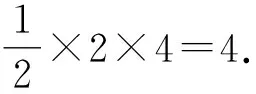
整理,得(3m2+4)y2-6my-9=0,

△=36m2+36(3m2+4)=144(1+m2)>0.

设M(x1,y1),N(x2,y2),则

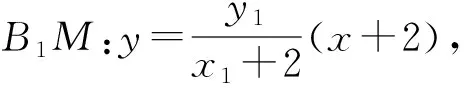
=-4,

故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

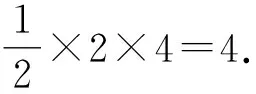
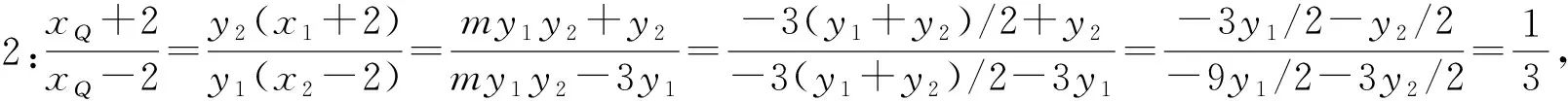
解得xQ=-4,故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

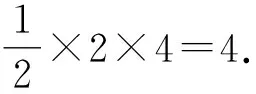
解法3(平移齐次化[2])设Q(x0,y0),直线MN:x+my+1=0(m≠0),

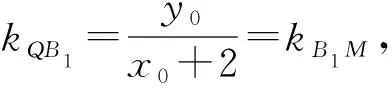
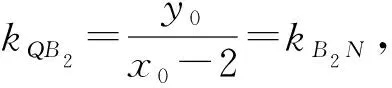
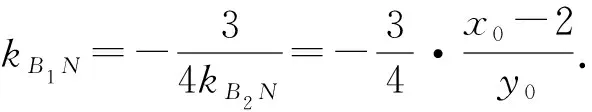
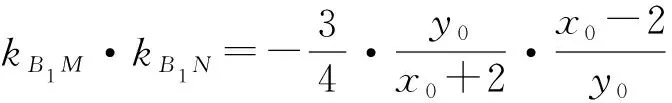
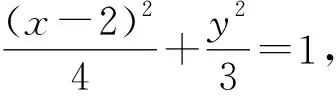
而直线MN的方程向右平移两个单位后得到x+my=1,则3x2-12x(x+my)+4y2=0.

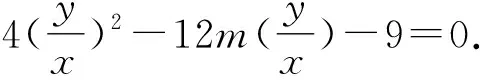
故kB1M,kB1N可以看作是上述方程的两根.

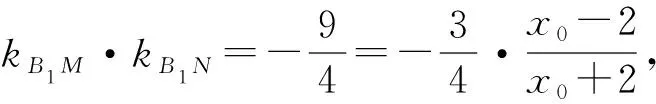
解得x0=-4.

故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

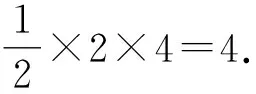
解法4 (斜率双用)设Q(x0,y0),M(x1,y1),N(x2,y2),直线B1Q的斜率

①

直线B2Q的斜率

②

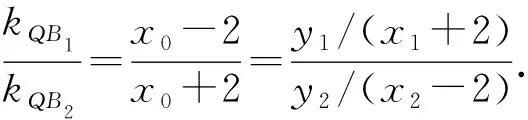
x2y1-2y1=λx1y2+2λy2.

③

由椭圆的第三定义可知,

④

⑤

将①代入④,得

⑥

将②代入⑤,得

⑦

整理,得x1y2-2y2=λx2y1+2λy1.

⑧

③-⑧,得

(λ+1)(x2y1-x1y2)=(2λ-2)(y2-y1).

⑨

而M,A1,N三点共线,得

即x2y1-x1y2=y2-y1.

⑩

联立⑨⑩,解得λ=3,

解得x0=-4,故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

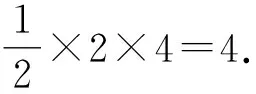
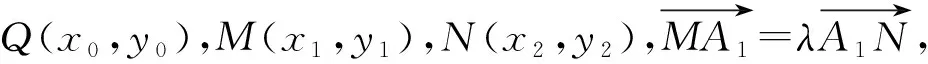
两式相减,得

=1-λ2.

整理,得x1-λx2=4λ-4.

而x1+λx2=-1-λ,

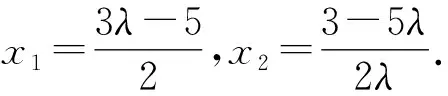
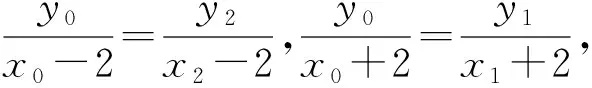
两式相除,得

解得x0=-4.

故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

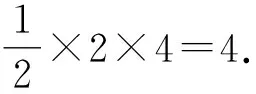
解法6 (二次曲线系) 设直线B1M:k1x-y+2k1=0,直线B2N:k2x-y-2k2=0,直线B1B2:y=0,直线MN:x-my+1=0,则过M,N,B1,B2四点的二次曲线系方程为(k1x-y+2k1)(k2x-y-2k2)+λy(x-my+1)=0.

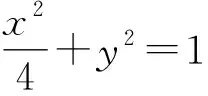
两式相减,得x=-4.

故点Q在直线x=-4上.

所以点Q到C1C2的距离d=4.

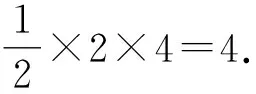
2 拓展延伸

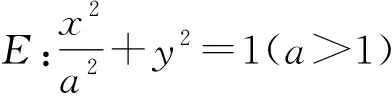
(1)求椭圆E的方程;

(2)证明:直线CD过定点.

通过对比不难发现,题1与题2有着异曲同工之妙,综合两个问题,我们可以得到如下结论:

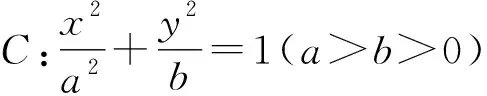
证明设直线AM:k1x-y+ak1=0,直线BN:k2x-y-ak2=0,直线B1B2:y=0,直线MN:x-my-t=0,则过M,N,B1,B2四点的二次曲线系方程为(k1x-y+ak1)(k2x-y-ak2)+λy(x-my-t)=0.

展开得k1k2x2+(1-λm)y2+(λ-k1-k2)xy+(-λt-ak1+ak2)y-a2k1k2=0.

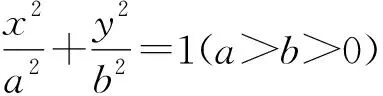
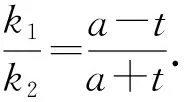
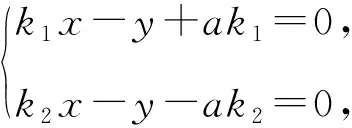
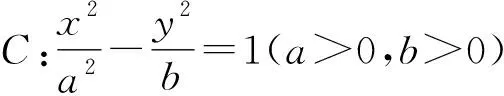
3 结束语

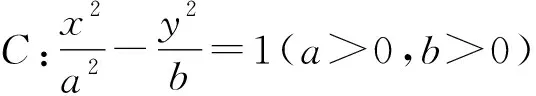
结论2、3、4的证明与结论1类似,这里不再赘述;对于焦点在y轴上的椭圆,也有类似结论,有兴趣的读者可以自行归纳整理.

进一步剖析结论的背景,可以看出两个问题出自“极点极线定理”: