例析曲线的公切线问题的求解策略
张秋珍
(北京大学附属中学莆田学校,福建 莆田 351100)
曲线的公切线问题是高考和质检试题的热点问题,如2016年高考新课标Ⅱ卷理16、2019年高考全国Ⅱ卷理20、2022年高考全国甲卷文20等.本文从福建省2023届高中毕业班适应性练习卷压轴题谈起,从多角度进行剖析,并拓展归纳公切线问题的常见类型,探析并总结其求解策略.
1 题目呈现
题目(福建省2023届高中毕业班适应性练习第22题)已知函数f(x)=(x+a)ex,a∈R.
(1)讨论f(x)在(0,+∞)的单调性;
(2)是否存在a,x0,x1,且x0≠x1,使曲线y=f(x)在x=x0和x=x1处有相同的切线?请证明你的结论.
2 解法赏析
2.1 第(1)问解析
解析当a<-1时,f(x)在区间(0,-a-1)单调递减,在区间(-a-1,+∞)单调递增;
当a≥-1时,f(x)在区间(0,+∞)单调递增.
2.2 第(2)问解析
解法1不存在a,x0,x1,且x0≠x1,使得曲线y=f(x)在x=x0和x=x1处有相同的切线.
证明如下:假设存在满足条件的a,x0,x1,
因为f(x)在(x0,f(x0))处的切线方程为
y-f(x0)=f′(x0)(x-x0),
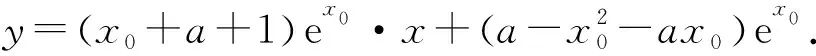
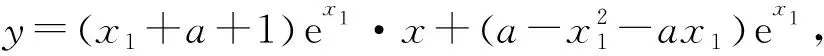
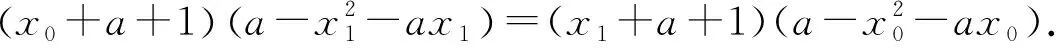
所以(x0+a+1)(x1+a+1)=1.
由(x0+a+1)ex0=(x1+a+1)ex1两边同乘以ea+1,得(x0+a+1)ex0+a+1=(x1+a+1)ex1+a+1.
令t0=x0+a+1,t1=x1+a+1,则
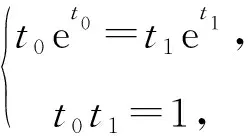

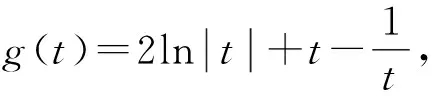
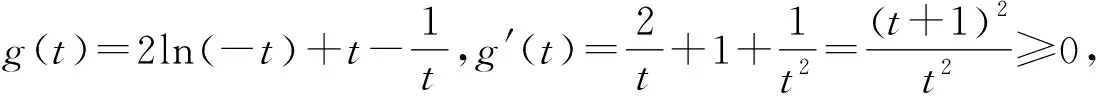
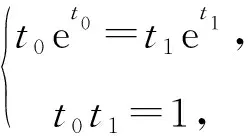
故不存在a,x0,x1且x0≠x1,使曲线y=f(x)在x=x0和x=x1处有相同的切线[1].
解法2假设存在满足条件的a,x0,x1,因为f(x)在(x0,f(x0))处的切线方程为
y-f(x0)=f′(x0)(x-x0),
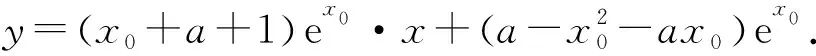
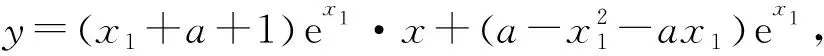
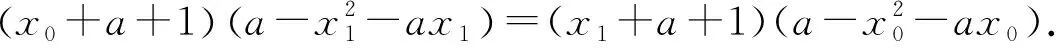
所以(x0+a+1)(x1+a+1)=1.
由(x0+a+1)ex0=(x1+a+1)ex1两边同乘以ea+1,得(x0+a+1)ex0+a+1=(x1+a+1)ex1+a+1.
令t0=x0+a+1,t1=x1+a+1,
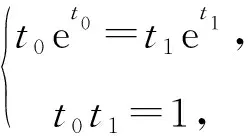
令h(t)=tet,则h(t0)=h(t1),且t0≠t1.
由(1)知,当t>-1时,h(t)单调递增,当t<-1时,h(t)单调递减,又当t>0时,h(t)>0,当t<0时,h(t)<0,所以若t0,t1存在,不妨设t1<-1 以下证明 所以g(x)在(1,+∞)上单调递减. 所以当x>1时,g(x) 所以(-t0)·(-t1)<1,与t0t1=1矛盾. 故不存在a,x0,x1且x0≠x1,使得曲线y=f(x)在x=x0和x=x1处有相同的切线. 例1已知函数f(x)=ex-ax+b,g(x)=x2-x,若曲线y=f(x)和y=g(x)在公共点A(1,0)处的切线相同,则a,b的值分别为____. 例2已知函数f(x)=lnx,g(x)=x2-x+2.证明:恰有两条直线与函数f(x),g(x)的图象都相切. 由g(x)=x2-x+2可得g′(x)=2x-1. 当0 所以F(x)在(0,1)上有一个零点,则F(x)在(0,+∞)上有且只有两个零点,故得证. 例3已和函数f(x)=lnx与g(x)=xa(x>0,a≠0),若存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线,则实数a的取值范围是____. 设直线l为曲线g(x)=xa(x>0,a≠0)在点(x2,g(x2))处的切线,g′(x)=axa-1, 因为x1>0,x2>0, 记h(x)=lnx-xa(a>0且a≠1),则 一般地,两个函数和的图象的公切线问题,常采用设各自的切点分别为(x1,f(x1)) ,(x2,g(x2)),再写出各自的切线方程,比较系数建立方程组,并求解方程组的方法处理.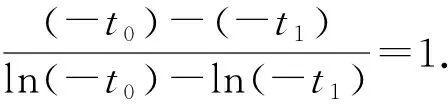
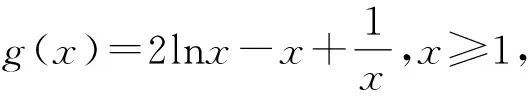
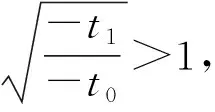
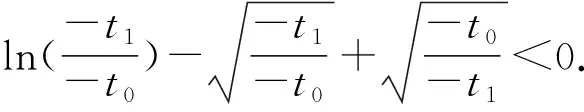
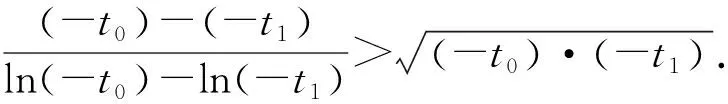
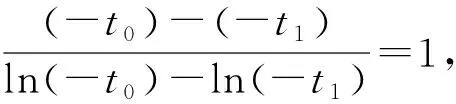
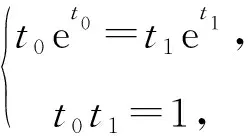
3 常见类型
3.1 求两个函数在公共点处的公切线与条数(接触型相切)
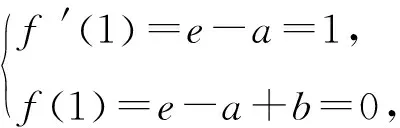
3.2 求两个函数(非接触型)相切的公切线与条数
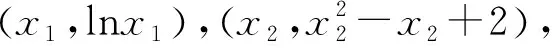
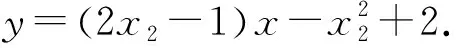

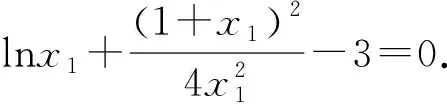

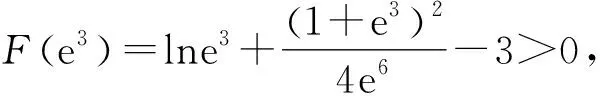

3.3 已知公切线的条数求参数范围
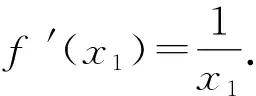
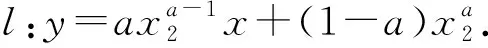
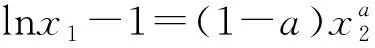
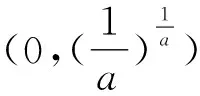


4 结束语

