一道不等式题的17种证法

李保强

(山东省郓城第一中学,山东 菏泽 274700)

不等式证明题技巧性都比较强.在日常的竞赛课教学中,教师可以引导学生从多种角度来解决,从而发散学生的数学思维,提高学生的解题能力.

1 竞赛模拟试题

题目已知a>0,b>0,a3+b3=2.证明:a+b≤2.

该题题干简短精炼,内涵却很丰富. 从各种角度对该题进行探究,不仅可以掌握不等式证明的方法和技巧,而且还可以领略其蕴含的数学思想方法.

2 证法探究

角度1 利用常见不等式.

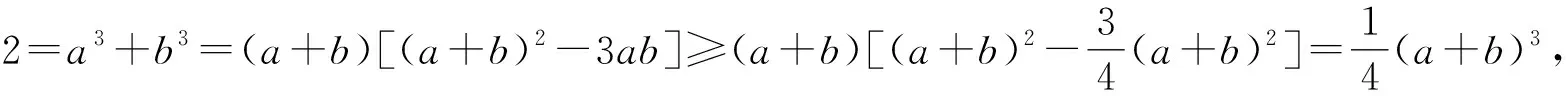
所以(a+b)3≤8,即a+b≤2.

所以(a+b)3≤8,即a+b≤2.

证法3由(a-b)(a2-b2)≥0,得

a3+b3≥ab2+a2b.

所以(a+b)3=a3+b3+3(a2b+ab2)≤a3+b3+3(a3+b3)=4(a3+b3)=8.

故a+b≤2.

证法4 因为a>0,b>0,所以

a+b≤2(a+b)3≤8

因为(a-b)(a2-b2)≥0显然成立,

所以a+b≤2成立[1].

证法5易知等号成立的条件是a=b=1.

构造均值不等式:

两式相加,得a3+b3+4≥3(a+b).

所以a+b≤2.

证法6 由柯西不等式,有

(a+b)(a3+b3)≥(a2+b2)2.

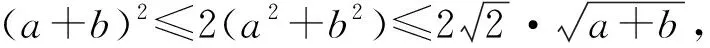
两边平方,得(a+b)4≤8(a+b).

即(a+b)3≤8.所以a+b≤2.

角度2 构造“一元二次方程”.

证法7设a,b是方程x2-mx+n=0的两正根,则a+b=m,ab=n.

由a3+b3=(a+b)[(a+b)2-3ab]=2,

得m(m2-3n)=2.

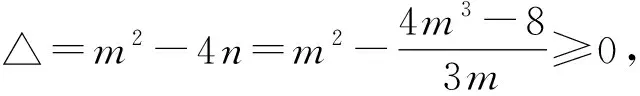
解得m≤2.

所以a+b≤2.

角度3 利用反证法.

证法8假设a+b>2,则a>2-b.

两边同时立方,得

a3>(2-b)3=8-12b+6b2-b3.

即8-12b+6b2-(a3+b3)<0.

即6b2-12b+6<0.

即(b-1)2<0,这是不可能的,因此a+b≤2.

角度4 利用函数的性质.

证法9 设h(x)=x3,如图1,易知h(x)是(0,+∞)上的凸函数.

图1 三次函数的凸性

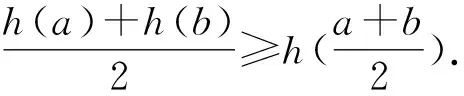
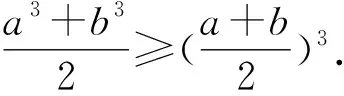
因此a+b≤2.

证法10不妨设a≤b,由a3+b3=2,知

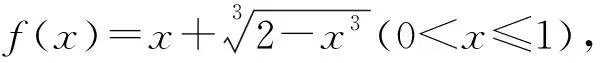
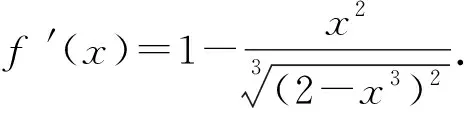
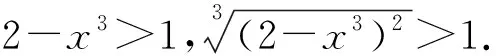
所以f′(x)>0,因此f(x)在(0,1]上单调递增.

所以f(x)≤f(1)=2.

所以a+b≤2[2].

角度5 构造等差数列.

证法11由a3+b3=2知a3,1,b3成等差数列,不妨设a≤b,则公差d=1-a3=b3-1≥0.

下面比较1-a,b-1的大小.

即 1-a≥b-1,所以a+b≤2.

角度6利用三角代换.

证法12设a+b=m,又a>0,b>0,令

a=mcos2θ,b=msin2θ,

代入条件a3+b3=2,得

所以m≤2,即a+b≤2.

角度7 构造向量.

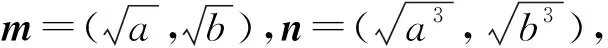
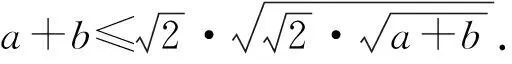
故a+b≤2.

角度8利用二项式定理.

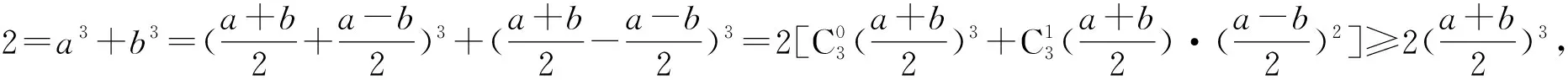
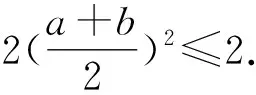
角度9利用解析几何思想.

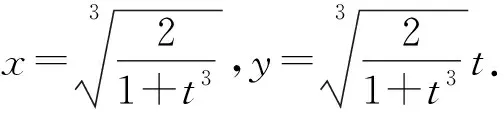
图2 曲线与直线

由图可知符合x3+y3=2的点都在满足x+y≤2的区域内.

设M={(x,y)|x+y≤2,x>0,y>0},

N={(x,y)|x3+y3=2,x>0,y>0},

如图2,可知N⊆M,因此a3+b3=2.

所以a+b≤2.

点评通过几何画板作出直线与曲线的图象,利用数形结合思想可知,∀(x,y)∈N,则(x,y)∈M,即a3+b3=2,即a+b≤2.从而使学生的数学思维从直观想象到逻辑推理,培养了学生直观想象和逻辑推理的核心素养[3].

角度10利用幂平均不等式.

证法16 由幂平均不等式

(其中xi>0,i=1,2,…,n,α<β),得

即a+b≤2.

点评由此可知,本题的背景是“幂平均不等式”,取α=1,β=3,n=2即得到本题的结论. 利用幂平均不等式,还可以得到本题的变式与推广.

角度11 构造恒等式.

3 结束语

这是一道可以有效训练学生数学思维的好题.通过探究这一道题,不仅可以复习基本不等式、柯西不等式,而且可以将基本不等式、柯西不等式、三角代换、构造向量、函数的单调性与凹凸性、幂平均不等式等常用方法联系起来.同时还可以复习韦达定理、判别式法、三角函数、平面向量、数列、函数、二项式定理、解析几何等内容.我们通过一道题就把高中数学的核心内容进行了串联,帮助学生构建了知识体系框架与脉络.