一道高考真题的解法探究与教学思考

曲 娜

(云南民族中学,云南 昆明 650221)

2023年高考数学全国卷落实党的二十大精神,全面贯彻党的教育方针,落实立德树人根本任务,促进学生德智体美劳全面发展;反映新时代基础教育课程理念,落实考试评价改革、高中育人方式改革等相关要求,全面考查数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析的核心素养,体现基础性、综合性、应用性和创新性的考查要求,突出理性思维,发挥数学学科在人才选拔中的重要作用.

1 题目呈现

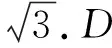
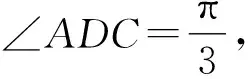
(2)若b2+c2=8,求b,c.

本题主要考查学生的逻辑推理和数学运算等数学学科核心素养,突出基础性要求,彰显综合性要求,蕴含中国高考评价体系四翼的要求,促进高中教学与义务教育阶段学习的有效衔接,同时也促进考教衔接.本题主要从正余弦定理、平面向量、平面几何、经典的几何定理等几个角度来进行分析,从而发现很多不同解法及其蕴含的数学思想.

2 题目解析

2.1 第(1)问解析

解法1 在△ABC中,S△ABC=S△ABD+S△ACD,即

解得a=4.

在△ABD中,利用余弦定理可知

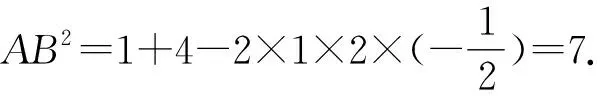
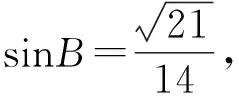
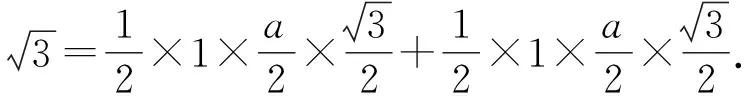
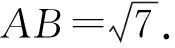
再利用余弦定理变式解得,

解法3 (余弦定理+面积公式)

在△ABC中,S△ABC=S△ABD+S△ACD,即

解得a=4.

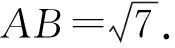
在△ABC中,再利用面积公式

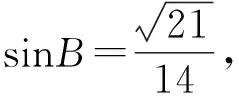
解法4(三次余弦定理)

在△ABC中,S△ABC=S△ABD+S△ACD,即

解得a=4.

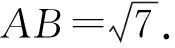
在△ACD中,利用余弦定理可知

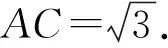
在△ABC中,利用余弦定理变式解得

解法5(二次余弦定理+正弦定理)

在△ABC中,S△ABC=S△ABD+S△ACD,即

解得a=4.

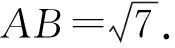
在△ACD中,利用余弦定理可知

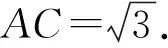
在△ABC中,利用正弦定理可知

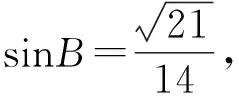
解法6(面积公式+两角和的正切公式)

在△ABC中,S△ABC=S△ABD+S△ACD,即

解得a=4.

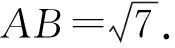
在△ACD中,利用余弦定理可知

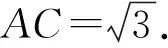
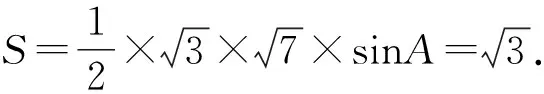
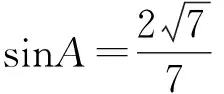
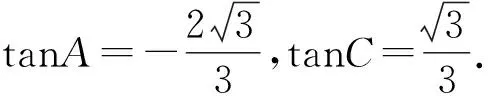
利用两角和的正切公式解得

2.2 第(2)问解析

解法1 (面积公式+平行四边形法则)

利用面积公式解得

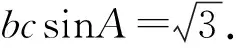
①

两边平方,得

4=b2+c2+2×b×c×cosA.

整理,得bccosA=-2.

②

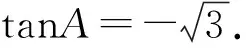
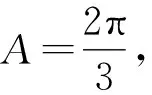
再由已知b2+c2=8,解得b=c=2.

解法2(中线长定理+面积公式)

由中线长定理可知,b2+c2=2(AD2+BD2).

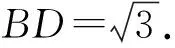
在△ABC中,S△ABC=S△ABD+S△ACD,

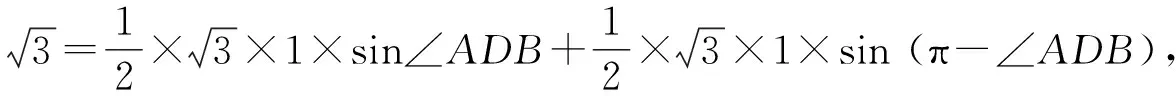
即AD⊥BC,底边中线也是底边高线.

所以△ABC是等腰三角形.

解得b=c=2.

解法3(中线长定理+面积公式+余弦定理)

由中线长定理可知,b2+c2=2(AD2+BD2).

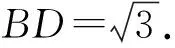
利用面积公式解得,

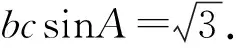
在△ABC中,由余弦定理可知

12=b2+c2-2×b×c×cosA.

解得bccosA=-2.

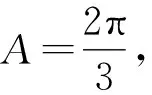
再由已知b2+c2=8解得b=c=2.

解法4(中线长定理+面积公式)

由中线长定理可知,b2+c2=2(AD2+BD2).

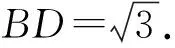
解法5(中线长定理+余弦定理+面积公式)

由中线长定理可知,b2+c2=2(AD2+BD2).

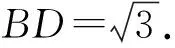
在△ACD中,由余弦定理可知,

③

在△ABC中,由面积公式解得

整理,得bsinC=1.

④

3 结束语

通过研究高考真题发现,我们在教学中应该多做微探究,让数学本质理解得更透彻.在课程标准指导下要重视教材,多练变式,让学生思维更生动,适当记忆经典定理、公式,多总结,让知识更系统.正所谓知其然还要知其所以然,刷百题不如吃透一题,高考改革万变不离其宗,这个宗就是对基础知识和基本概念的深入理解和灵活掌握,这就要求我们能够寻根溯源,抓住问题的本质.引导我们备课更加注重思维能力和思想方法的渗透,不能死记公式,而是关注学生,引导学生自主学习、合作探究,真正掌握知识,学会灵活运用,不断提高自身的思维能力[1].