2023年新高考Ⅰ卷第22题的五种解法
卢会玉
(西北师范大学附属中学,甘肃 兰州 730070)
自新高考施行以来,有很多学生吐槽数学题通常都是“满纸的不超纲,但就是不正常说话!”不难发现,命题者是想通过改变固定的命题模式,指导教师和学生实现两个转变:从解题到解决问题的转变;从死板的刷题到培养思维的转变[1].这是在大力推行核心素养的背景下进行的一次具有革命性的变化!2023年新高考Ⅰ卷第22题让我们再一次感受到了数学思维训练的重要性,下文从三角函数、直线的参数方程等五种不同的角度对该题进行了解析.
1 试题呈现
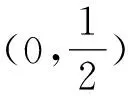
(1)求W的方程;
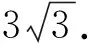
2 试题解析
2.1 第(1)问解析
解析设动点P(x,y),则由题意可得
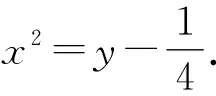
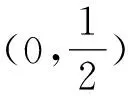
2.2 第(2)问解析
解法1 (利用三角函数和放缩法解题)不妨设A,B,D在W上,显然矩形ABCD每条边所在直线的斜率都存在.因为此时AB⊥AD,则设AB的倾斜角为θ,所以AD的倾斜角为90°+θ.

由抛物线和矩形的对称性,不妨设0<θ≤45°.
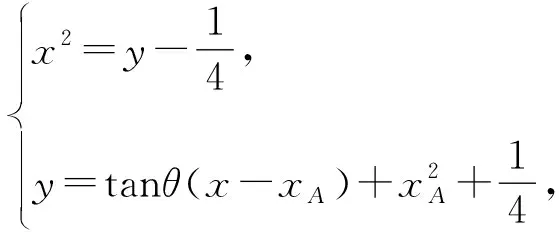
所以xA+xB=tanθ.则xB=tanθ-xA.
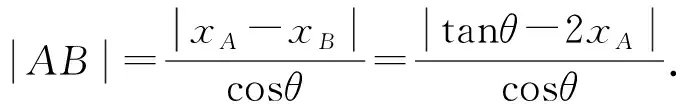
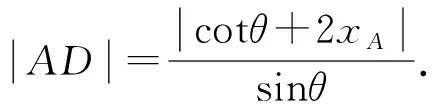
所以矩形ABCD的周长为
因为0<θ≤45°,所以0 解法2(利用直线参数方程和放缩法解题)不妨设A,B,D在W上,显然矩形ABCD每条边所在直线的斜率都存在. 因为此时AB⊥AD,则设AB的倾斜角为θ,所以AD的倾斜角为90°+θ. 直线AD的参数方程为 t2cos2θ+t(2mcosθ-sinθ)=0. 以下同解法1. 解法3(利用常规根与系数关系和放缩法解题)不妨设A,B,D在W上,显然矩形ABCD每条边所在直线的斜率都存在. 所以xA+xB=k,则xB=k-xA, 所以矩形ABCD的周长为 又由抛物线和矩形的对称性可知,-1≤k≤1,k≠0,不妨使0 又根据|a|+|b|≥|a+b|(当且仅当ab≥0时取等号), 解法4(利用常规根与系数关系和分段函数解题)不妨设A,B,D在W上,显然矩形ABCD每条边所在直线的斜率都存在. 设直线AB的方程为y=kx+m, Δ=k2+4m-1>0, 所以xA+xB=k,则xB=k-xA, 由抛物线和矩形的对称性可知,-1≤k≤1,k≠0,不妨使0 以下同解法3. 即(x1-x2)(x1-x3)+(y1-y2)(y1-y3)=0. 所以1+(x1+x2)(x1+x3)=0. 即(x1+x2)(x1+x3)=-1. 所以矩形ABCD的周长为 因为(x1+x2)(x1+x3)=-1, 所以不妨设(x1+x2)2≤(x1+x3)2, 所以2(|AB|+|AD|) 当且仅当x2+x3=2x1时取等号. 又根据|a|+|b|≥|a-b|(当且仅当ab≤0时取等号), 令m=x1+x2,由(x1+x2)(x1+x3)=-1,可不妨设m∈(0,1], 以下同解法3. 不难发现,以上五种方法有一个共同的特点,就是都利用了不等式性质进行了放缩运算,达到了减少变量的目的,最后基本都变换为一个利用函数单调性求最值的问题. 所以,遇到思维量较大的题目,我们一定要有明确的目标,有的放矢.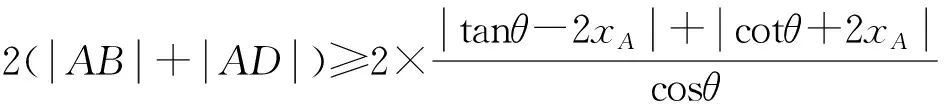
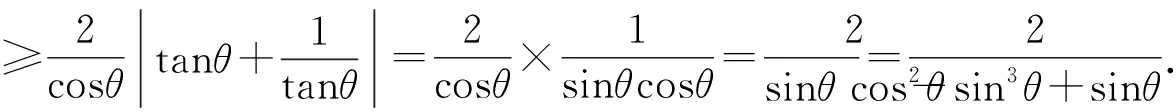
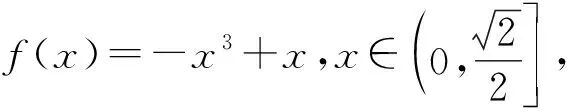
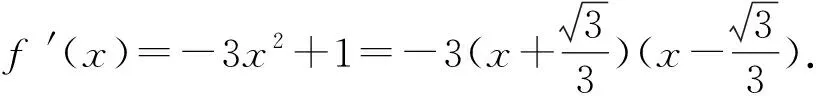
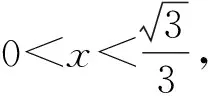
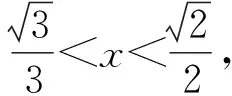
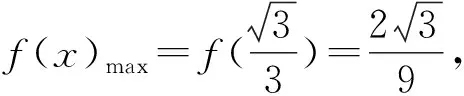
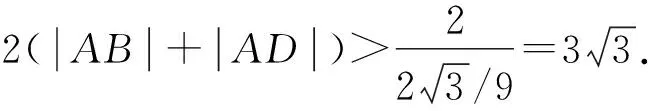
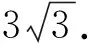
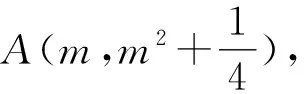
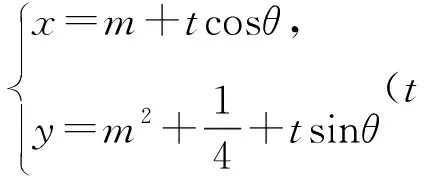
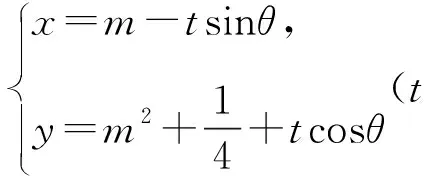
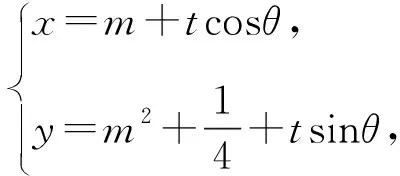
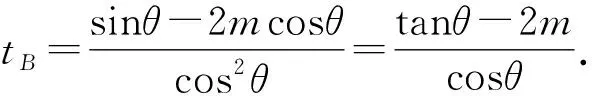
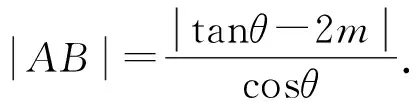
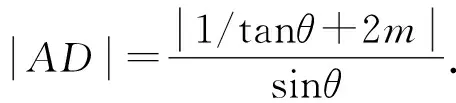
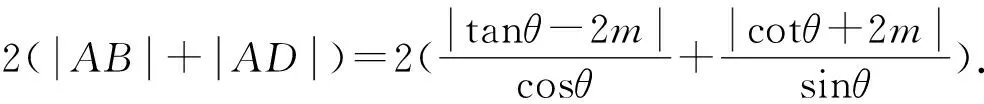
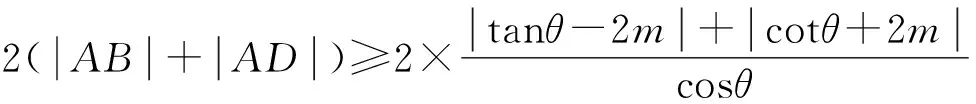
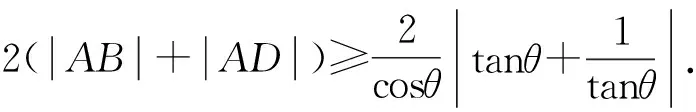
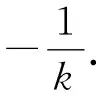

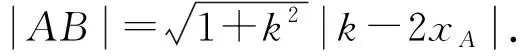
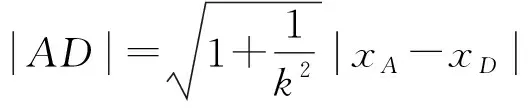
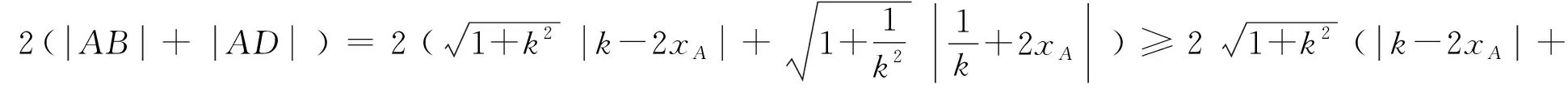
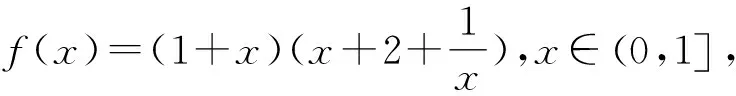
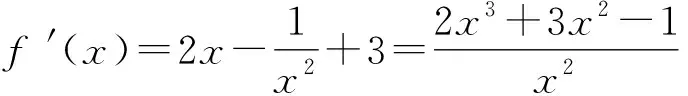
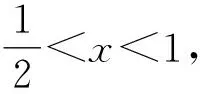
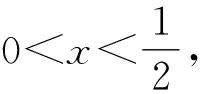
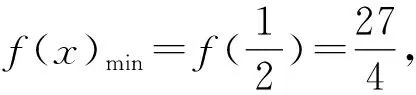
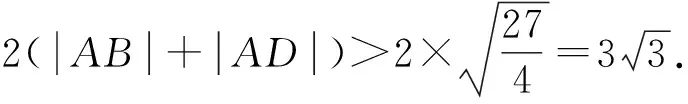
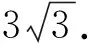
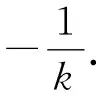
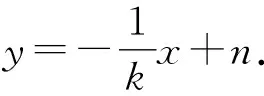
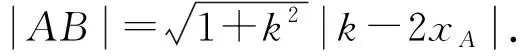
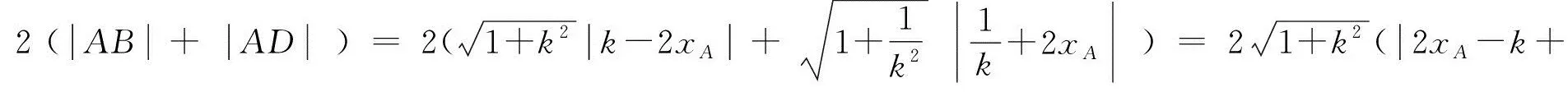
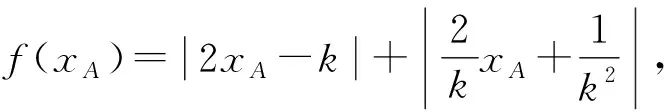
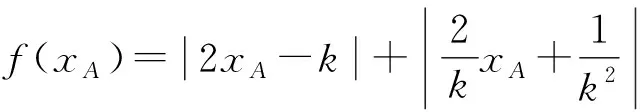
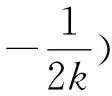
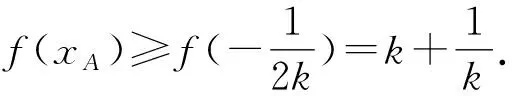
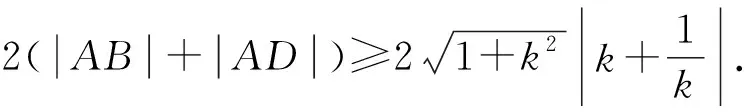
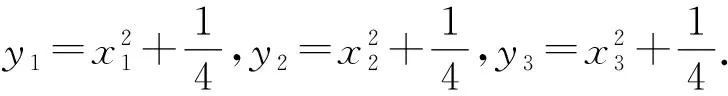
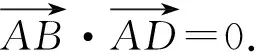
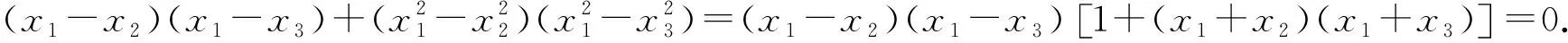
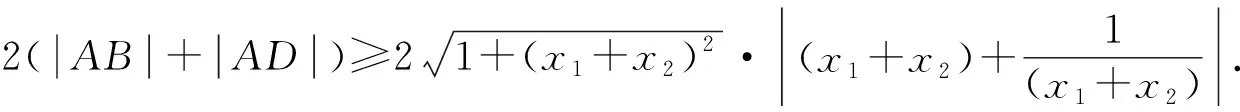
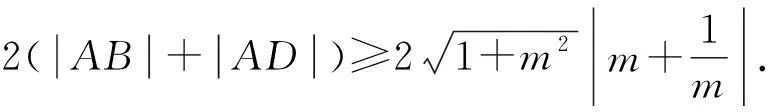
3 结束语

