多方视角觅答案 登高望远探背景
——探究2022年高考北京卷第20题
林国红
(广东省佛山市乐从中学,广东 佛山 528315)
题目呈现(2022年高考北京卷第20题)已知函数f(x)=exln(1+x).
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(3)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
由于问题(1)与(2)较为简单,只给出答案,本文主要对问题(3)进行探究.
1 问题(1)与(2)的答案
故f′(0)=e0(ln1+1)=1.
故曲线y=f(x)在点(0,0)处的切线方程为y=x.
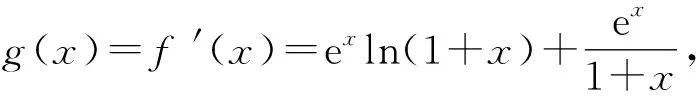
因为x≥0,
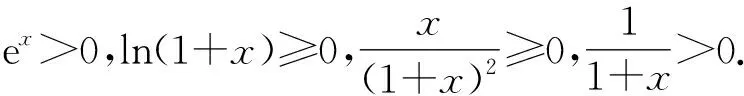
从而可得g′(x)>0.
所以g(x)在[0,+∞)上的单调递增.
2 问题(3)的证法探究
视角1直接作差,构造差函数.
证法1 设t∈(0,+∞),令h(x)=f(x+t)-f(x)(x≥0),则
h(x)=ex+tln(1+x+t)-exln(1+x),
当x≥0时,由(1),可知
所以f(x)在[0,+∞)上单调递增.
因为t∈(0,+∞),x≥0,
所以x+t>x.
从而可得f(x+t)>f(x).
即ex+tln(1+x+t)>exln(1+x).
故ex+tln(1+x+t)-exln(1+x)>0.
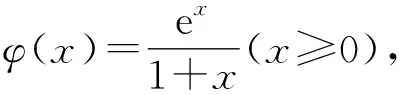
所以φ(x)在[0,+∞)上单调递增.
因为t∈(0,+∞),x≥0,
所以x+t>x.
从而可得φ(x+t)>φ(x).
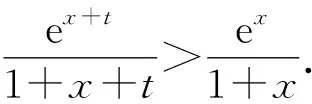
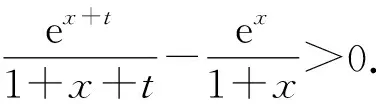
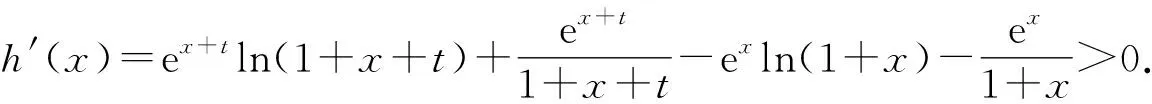
故h(x)在[0,+∞)上单调递增.
因为s∈(0,+∞),
所以h(s)>h(0).
即f(s+t)-f(s)>f(t)-f(0),且f(0)=0.
所以f(s+t)-f(s)>f(t).
即f(s+t)>f(s)+f(t).
证法2 令h(x)=f(x+t)-f(x)(x≥0),则
h′(x)=f′(x+t)-f′(x).
由(2)可知,
g(x)=f′(x)在[0,+∞)上单调递增.
由于s,t∈(0,+∞),x≥0,则
x+t>x.
从而可得f′(x+t)>f′(x).
即h′(x)>0.
所以h(x)在(0,+∞)上单调递增.
于是h(s)>h(0).
即f(s+t)-f(s)>f(0+t)-f(0),且f(0)=0.
所以f(s+t)-f(s)>f(t).
即f(s+t)>f(s)+f(t).
评注一般来说,证明函数不等式f(x)>g(x)恒成立,可设F(x)=f(x)-g(x),则f(x)>g(x)恒成立F(x)>0恒成立,作差法是证明不等式成立的最常规做法,思路自然.证法1作差后,通过探究具体函数的单调性来证明,运算量较大;证法2则利用问题(2)的结论来证明,证明过程简洁.
视角2 放缩法.
证法3 (利用ex>1+x放缩)因为f(x)=exln(1+x),s,t∈(0,+∞).
要证明f(s+t)>f(s)+f(t),即证明
es+tln(1+s+t)>esln(1+s)+etln(1+t).
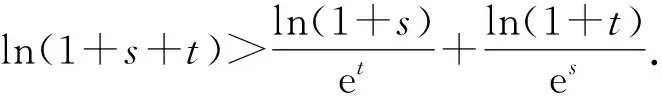
因为ex>1+x(x>0),
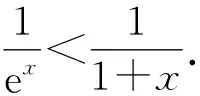
故只需证明
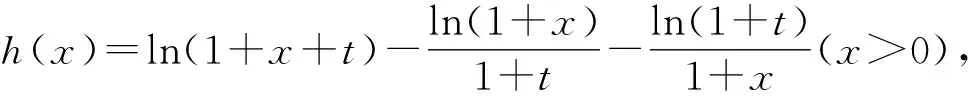
所以h(x)在(0,+∞)上单调递增.
故h(s)>h(0)=ln(1+t)-ln(1+t)=0.
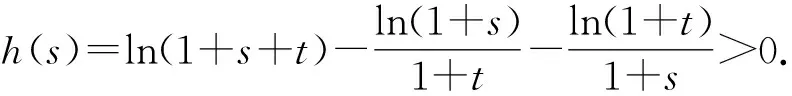
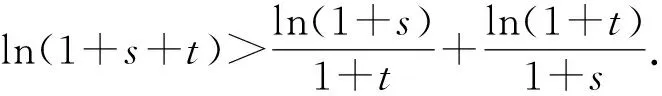
所以f(s+t)>f(s)+f(t).
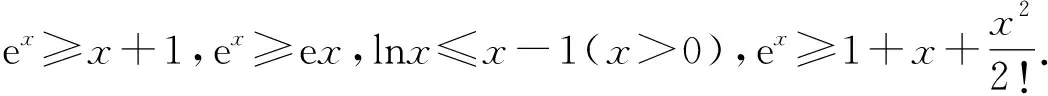
视角3 更换主元法.
证法4 令h(s)=f(s+t)-f(s)-f(t)(s>0),则
h′(s)=f′(s+t)-f′(s)=g(s+t)-g(s).
由(2)可知,g(x)在[0,+∞)上单调递增.
由于s,t∈(0,+∞),则s+t>s.
从而可得g(s+t)>g(s).
即h′(s)>0.
所以h(s)在(0,+∞)上单调递增.
于是h(s)>h(0),且f(0)=0.
从而h(0)=f(t)-f(0)-f(t)=0.
故h(s)=f(s+t)-f(s)-f(t)>0.
所以f(s+t)>f(s)+f(t).
评注“横看成岭侧成峰,远近高低各不同.”同一事物从不同角度看,会有不同的认识.由于问题涉及两个变量,且两个变量彼此独立,所以可以把其中一个变量看作未知数(确立为主元),另一个先固定,从而转化为单变量问题.这样能排除参数间的干扰,简化问题结构,可以化繁为简,化难为易,使求解过程更加简捷[1].
视角4高观点.
证法5 由s,t∈(0,+∞),不妨设0 由拉格朗日中值定理,可得∃ξ∈(s,s+t),有 ∃η∈(0,t),有 由(2)可知,g(x)=f′(x)在[0,+∞)上单调递增,且f(0)=0. 因为ξ>η, 所以f′(ξ)>f′(η). 于是f(s+t)-f(s)>f(t). 所以f(s+t)>f(s)+f(t). 评注拉格朗日中值定理不在高中的学习范围内,学生不需要掌握,但其解题思路新颖,过程简捷,能体现试题本质内涵,值得学习. 问题(3)中的二元不等式f(s+t)>f(s)+f(t)在形式上十分优美,自然的想法是:什么样的函数f(x)在满足s,t∈(0,+∞)时,有f(s+t)>f(s)+f(t)?问题(3)的命题背景是什么? 由s,t∈(0,+∞),不妨设0 作出函数f(x)=exln(1+x)的图象(如图1),作直线AB,CD.由图1可知,直线AB,CD的倾斜角均为锐角,且直线CD的倾斜角大于直线AB的倾斜角,即kCD>kAB. 图1 f(x)=exln(1+x)的图象 事实上,由证法5,可得 因为ξ>η,所以f′(ξ)>f′(η). 从而kCD>kAB. 显然kCD>kAB正是试题的几何背景. 从问题(1)可知,函数f(x)=exln(1+x)在[0,+∞)上单调递增;由问题(2)可知,g′(x)>0,即f″(x)>0,所以可得函数f(x)=exln(1+x)在[0,+∞)是下凸函数,且单调递增. 那么,是不是单调递增的下凸函数f(x)都有性质:当s,t∈(0,+∞)时,有f(s+t)>f(s)+f(t)? 答案是肯定的,下面给出更一般的结论. 定义函数f(x)在区间D内有定义,若对于任意的x1,x2∈D和任意的0<λ<1,恒有 λf(x1)+(1-λ)f(x2) >f[λx1+(1-λ)x2], ① 则称f(x)在区间D内是下凸函数,简称下凸.若上述不等式反向恒成立,则称f(x)在区间D内是上凸函数,简称上凸. 性质若f(x)在区间D内是下凸函数,x1,x,x2∈D且x1 ② 证明在下凸函数的定义中,若x1 λx1+(1-λ)x2=x, 则λf(x1)+(1-λ)f(x2)>f(x), (1)由λf(x1)+(1-λ)f(x2)>f(x),得 λf(x1)-λf(x2)>f(x)-f(x2). 即λ[f(x2)-f(x1)] 注意到x1 (2)由λf(x1)+(1-λ)f(x2)>f(x),得 -(1-λ)f(x1)+(1-λ)f(x2)>f(x)-f(x1). 即(1-λ)[f(x2)-f(x1)]>f(x)-f(x1). 注意到x1 综合(1)(2),可得 证明(1)当t=s时,不等式r (2)当t≠s时,由r 由t 评注函数凹凸性是函数的一种特殊性质,其相关知识十分丰富.以函数凹凸性为背景的题目屡见不鲜,这些试题情景新颖,能考查学生的创新能力和潜在的数学素质,常作为压轴题出现,这也表明:高等数学的相关理论是命制一些具有创新力与区分度的高考试题的重要来源[3].虽然在高中课本中没有这方面的内容,但若能多了解一些函数凹凸性的相关理论知识,可以“登高望远”,开拓思维,养成对试题背后的内在关系分析与思考的习惯,便于找到问题的本质内涵,确定解题方向,寻找简捷的解题途径. 高考试题是精心之作,每年的高考题在命题角度、题型、难度等方面都进行了充分考量,是知识、能力和思想方法的载体,大多都蕴含着深刻的背景、丰富的数学思想.近年来,高考的命题者通过挖掘高等数学中的一些素材来命制高考试题,此类试题也逐渐引起大家的关注[4].但这并不意味着要将过多的高等数学知识下放到中学,加重中学的负担,应该是站在高观点的角度看待问题,将研究的问题引向深入,探索隐藏在题目背后的奥秘,挖掘题目的真正内涵,能够找到解决这个问题与解决其他问题在思维上的共性.这样,我们才能领会到试题命制的深刻背景,才能跳出题海,真正做到触类旁通,举一反三.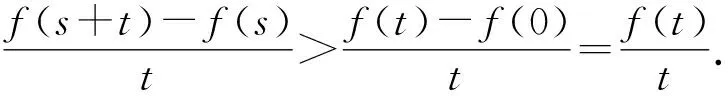
3 问题(3)的命题背景探析
3.1 几何背景
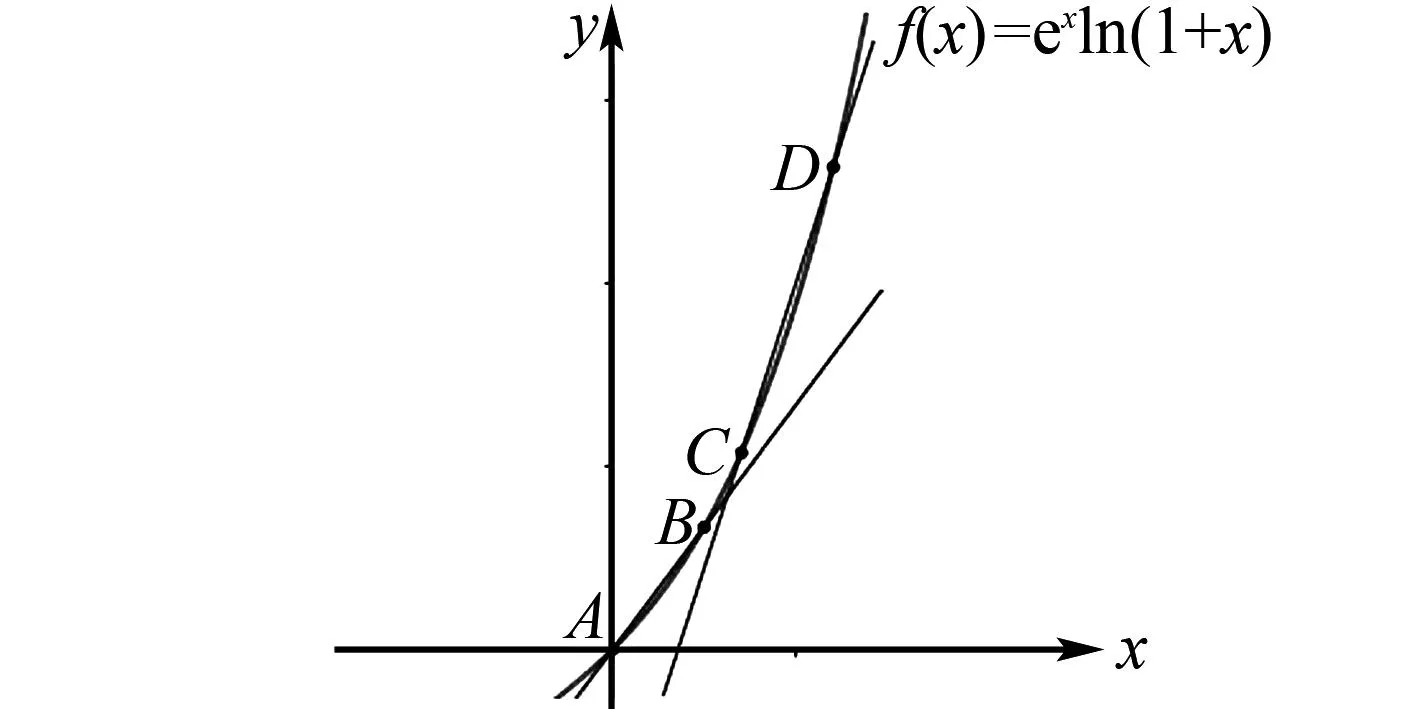
3.2 高等数学背景
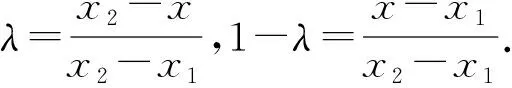
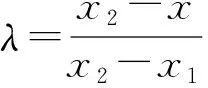

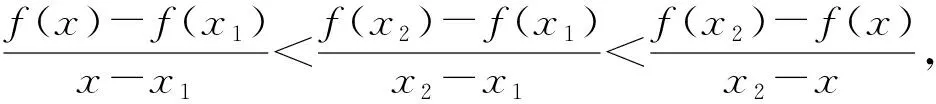
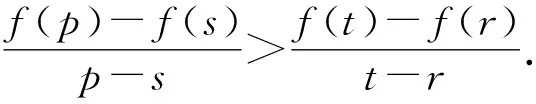
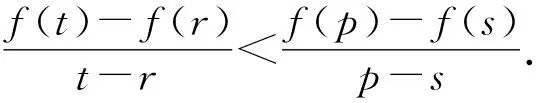
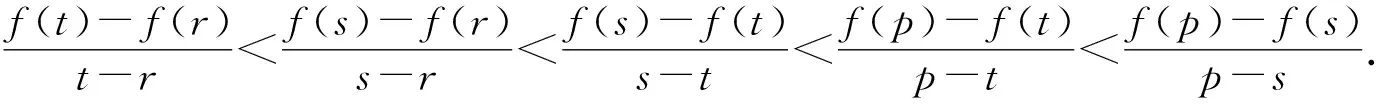
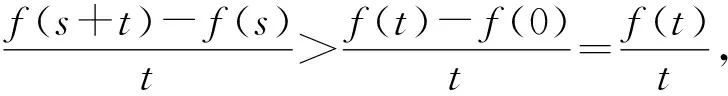
4 结束语

