用伸缩变换突破高考难题

李昌成

(新疆乌鲁木齐市第八中学,新疆 乌鲁木齐 830002)

圆锥曲线是高中数学的重要内容之一,所有学生在这一内容上都投入了很大的精力.每年高考的圆锥曲线解答题运算量都很大,考生普遍得分率很低.对这一现象,我们都在思考是否有解决的办法.我们可否将教材上的圆、椭圆、坐标变换这三个内容整合在一起,以坐标变换为纽带将圆的特有性质应用于有关椭圆的考题中?坐标变换(这里主要研究伸缩变换)是仿射几何的范畴,为了解题需要,高中数学教学应达到什么程度?或者说,应补充哪些理论知识?

1 理论准备

我们通过教学实践研究发现,在教材现有知识的基础上稍微拓展一下理论就可以应用伸缩变换解题,尤其是突破一些高考的难题,大有裨益.

引理1 伸缩变换前后,共线点依然共线.

引理2 伸缩变换前后,平行线依然平行,相交线依然相交,直线和曲线的位置关系不变.

引理3 伸缩变换前后,共线(平行)的线段长度比不变.

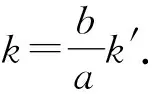
引理5伸缩变换前后,封闭图形的面积满足S=abS′.

2 应用伸缩变换解题

题型1 证明直线过定点(三点共线).

(1)求E的方程;

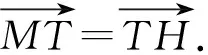
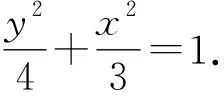
下面应用伸缩变换解答(2).

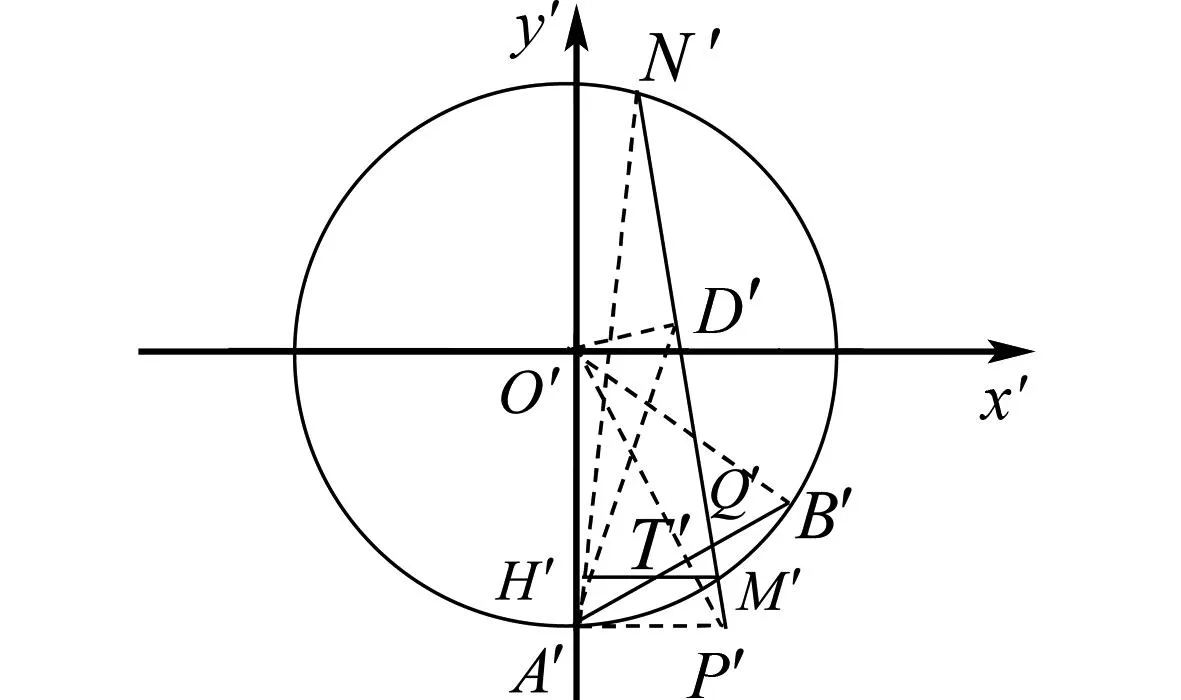
图1 例1解析示意图

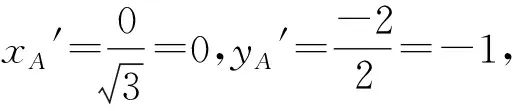
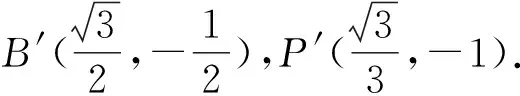
设M′N′与A′B′相交于点Q′,连接A′P′,A′N′,O′P′,O′B′.过点O′作O′D′⊥M′N′于点D′,连接A′D′,由两点间距离公式易得

|A′B′|=|OA′|=|OB′|=1.

所以ΔO′A′B′是正三角形.

结合图1,猜想N′,H′,A′共线,也就是N′H′过定点A′.下面证明猜想.

要证明N′,H′,A′共线,只需证明

①

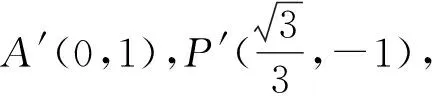
而M′T′∥x轴,因此A′P′∥M′T′.

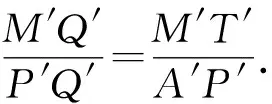
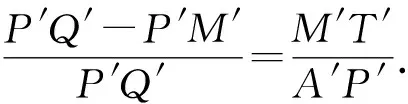
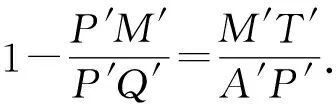
②

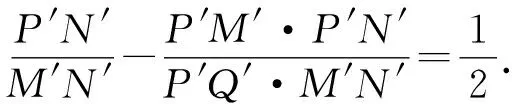
③

因为A′P′是圆O′的切线,

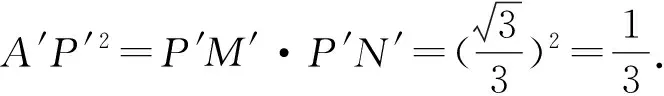
④

⑤

因为A′P′⊥O′A′,O′D′⊥M′N′,

所以O′,A′,P′,D′四点共圆.

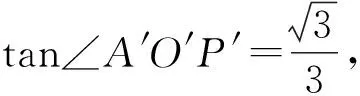
于是∠O′D′A′=∠O′P′A′=60°.

而∠A′D′P′=90°-∠O′D′A′=30°,

∠Q′A′P′=90°-∠O′A′B′=30°,

所以∠A′D′P′=∠Q′A′P′.

因此ΔA′D′P′∽ΔQ′A′P′.

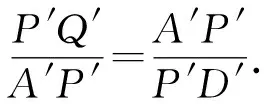
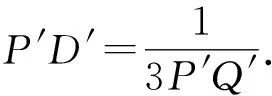
⑥

⑦

结合投影和垂径定理,⑦成立.

所以猜想成立.

因此,直线H′N′过定点(0,-1).

由引理1得,直线HN过定点(0,-2).

评注用传统方法解答此题运算量非常大,有兴趣的同仁可以试做一下,在高考有限的时间内考生难以完成.伸缩变换解法几乎没有运算,全程只有逻辑推理,思路清晰,解题耗时较少,正确率也高.

题型2 证明存在性问题

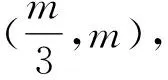
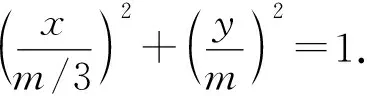
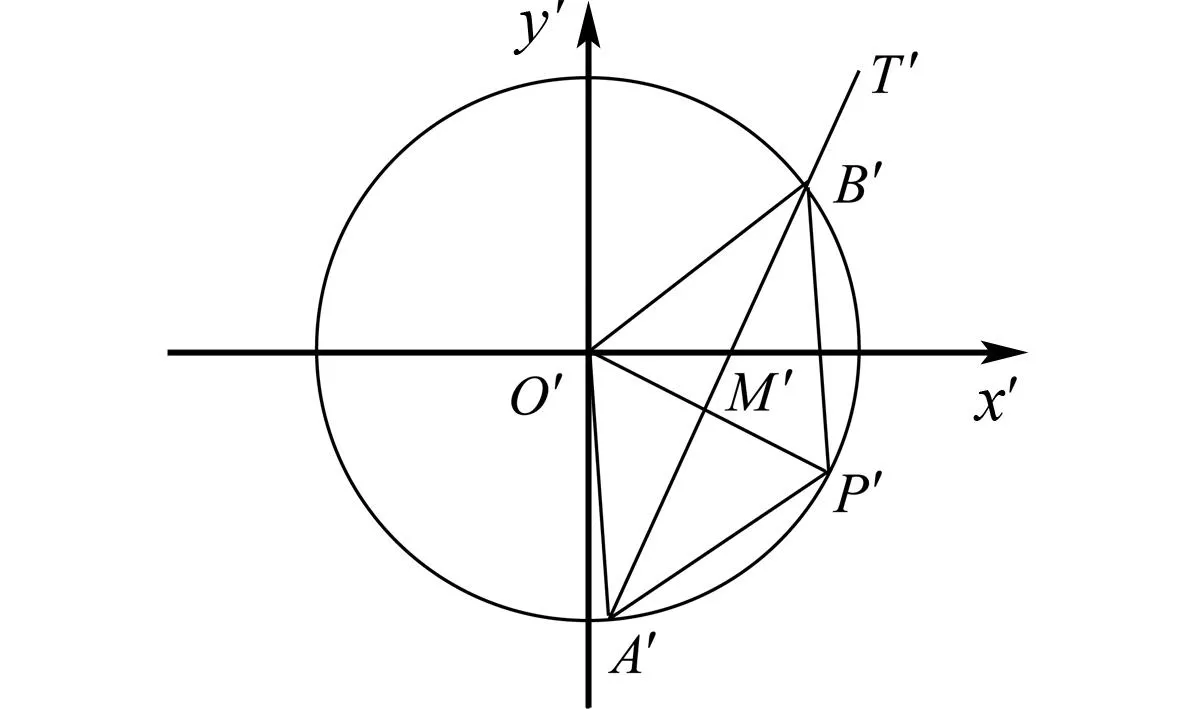
图2 例2解析示意图

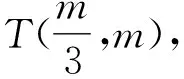
记直线l在伸缩变换前后的斜率分别为k,k′.则直线l′的点斜式方程为y′=k′(x′-1)+1.

由引理2知,四边形O′A′P′B′是平行四边形,进而结合圆的性质可判断其为菱形.

所以△O′A′P′是边长为1的正三角形.

所以O′M′⊥A′B′.

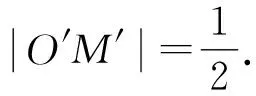
将y′=k′(x′-1)+1变形为k′x′-y′-k′+1=0,

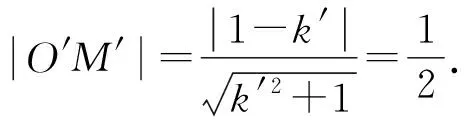
评注本例通过伸缩变换后得到的四边形非常特殊,这为后续计算提供了方便.如果按照常规办法求解,一定不可避开大量的字母运算,甚至解题思路受阻,不知如何应用平行四边形这个条件.

题型3 证明垂直.

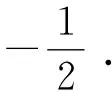
(1)求C的方程,并说明C是什么曲线;

(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为点E,连接QE并延长交C于点G.证明△PQG是直角三角形[2].

下面应用伸缩变换解答(2).

图3 例3解析示意图

设P′(s,t),由引理1结合单位圆性质知Q′(-s,-t),E′(s,0).

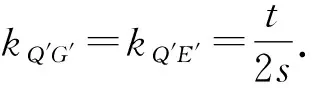
在圆O′中,PQ是直径,所以P′G′⊥Q′G′.

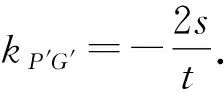
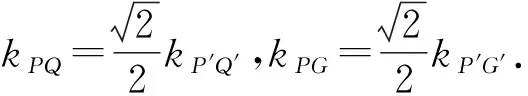
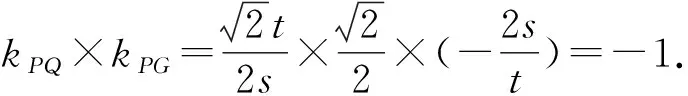
于是PQ⊥PG.

所以ΔPQG是直角三角形.

评注本题通过伸缩变换后,借助直径所对圆周角为直角巧妙地证明了问题,省去了判断直角顶点的麻烦,可谓一箭双雕.事实上,用传统办法证明不仅运算量大,而且很难一次性找准直角顶点.

题型4 求(最)值.

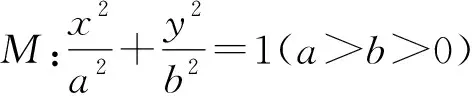
(1)求M的方程;

(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.

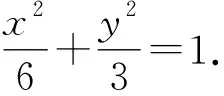
下面应用伸缩变换解答(2).

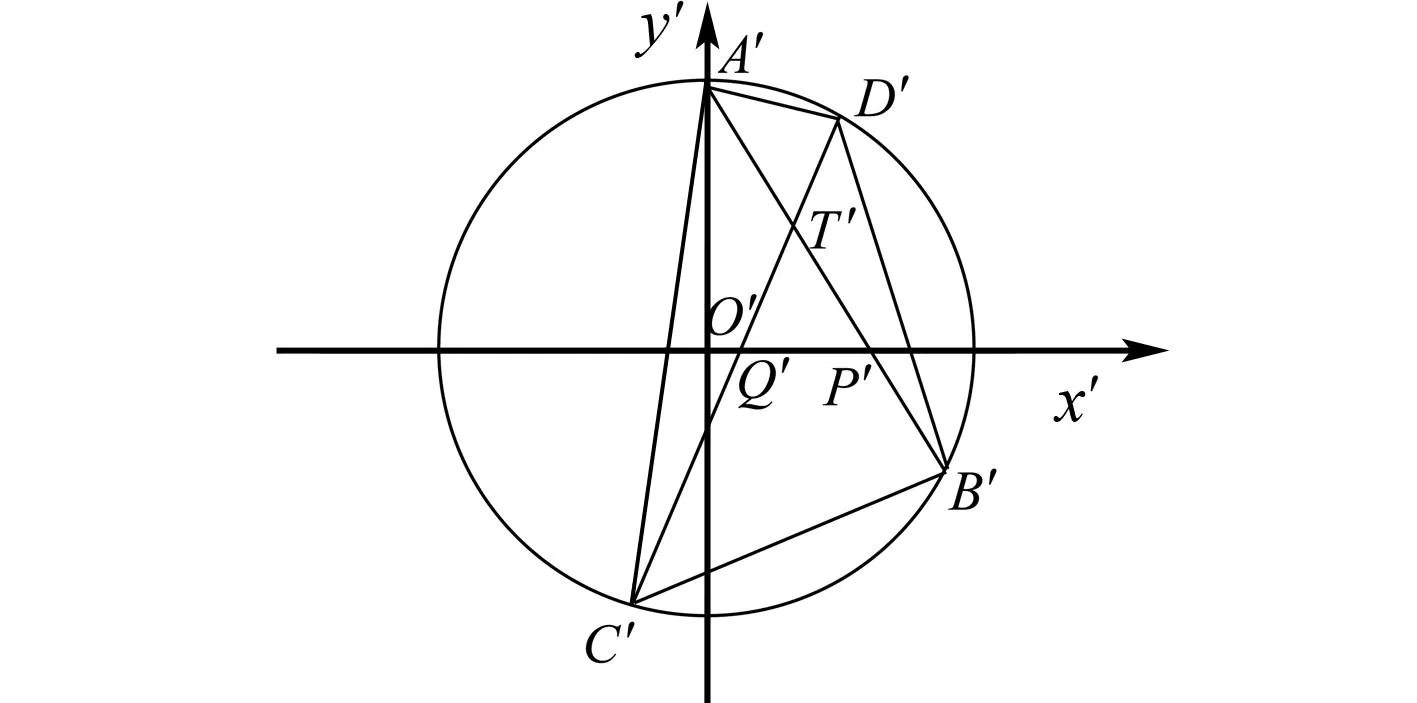
图4 例4解析示意图

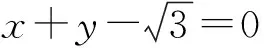
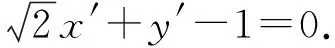
根据已知,可设直线CD的方程为x-y+t=0,

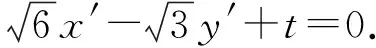
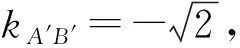
所以直线A′B′的倾斜角为π-α.

设A′B′,C′D′与x轴分别交于P′,Q′,A′B′与C′D′交于点T′,那么∠T′Q′P′=∠T′P′Q′=α.

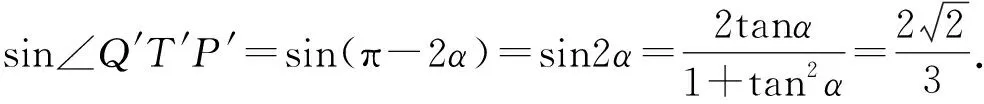
在圆O′中,由垂径定理易得

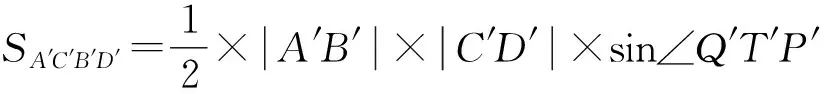
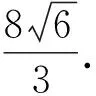
评注通过伸缩变换得到的四边形内包含的等腰三角形为构造面积函数作了铺垫,圆的特性使面积函数关系简单,这样处理最值问题非常方便.在推理中夹杂着少量运算,这种解题充满着思辨性.

3 结束语

利用伸缩变换,结合单位圆的特性解题非常方便.我们在教学中可以利用大单元教学理论对教材知识进行合理整合,根据解题需要对相关知识进行适当拓展,这样不仅可以优化学生的知识结构,还可以拓广学生的解题思维,增加解题方法,提高解题准确率.