完善数学知识体系 培养数学核心素养——2021年广东省中考数学第25题难点分析及教学启示

武也文

(江苏省南京市第六十六中学,江苏 南京 210037)

二次函数是初中数学的重要内容,是历年中考热点问题,承载着一定的选拔性功能,对学生而言具有一定的难度.在2023年中考第一轮复习时,笔者借助2021年广东省中考数学第25题,帮助学生梳理二次函数的知识,建构完备的知识体系,提升学生的数学核心素养．

1 试题呈现

已知二次函数y=ax2+bx+c的图象过点(-1,0),且对任意实数x,都有4x-12≤ax2+bx+c≤2x2-8x+6．

(1)求该二次函数的解析式;

(2)若(1)中二次函数图象与x轴的正半轴交点为A,与y轴交点为C.点M是(1)中二次函数图象上的动点．问在x轴上是否存在点N,使以A、C、M、N为顶点的四边形是平行四边形．若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.

本题主要考查一次函数、二次函数的图象与性质、函数与方程、不等式之间的联系等数学核心知识及函数思想、方程思想、转化思想、数形结合思想、分类思想等重要的数学思想方法,需要学生具有完备的数学知识体系,对学生的数学核心素养要求较高．

2 试题的思路突破及难点分析

2.1 思路突破

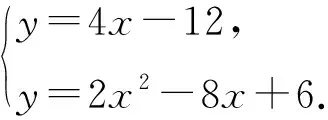
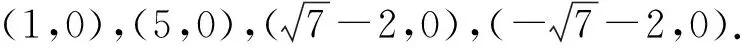
2.2 难点分析

本题是一道压轴题,主要考查学生对初中代数核心知识的综合运用能力．虽然本题的题干简洁,学生读起来一目了然,但是题型新颖且起点较高,学生不知如何解决问题．以下从该题的主要难点给出几点反思．

难点之一:一般来说,压轴题中的问题是按照从易到难的过程来设置的,但本题的问题(1)既是本题的亮点,也是本题的难点.许多学生做不出这道题,就是没有弄清楚题目中的条件应该如何使用,如何转换成有效信息．问题(1)求该二次函数的解析式,学生最常用的方法是待定系数法,但函数y=ax2+bx+c有三个系数未知,题目中的条件只给了一个已知点(-1,0),直接用待定系数法不能解决这个问题,怎么办?

难点之二:考查一次函数、二次函数、不等式和方程等数学知识之间的内在联系,并借助函数图象分析、解决问题的能力．问题(1)对于学生而言从“4x-12≤ax2+bx+c≤2x2-8x+6”这个连续不等式,或许不难想到三个函数:y1=4x-12,y2=2x2-8x+6,y3=ax2+bx+c．但条件中的两个“≤”有什么作用,怎么使用呢?这就要求学生必须借助函数的图象来分析问题,通过画示意图发现函数y1=4x-12,y2=2x2-8x+6的图象只有一个交点(3,0),如图1所示;根据 “4x-12≤ax2+bx+c≤2x2-8x+6”这个条件,y2=2x2-8x+6的图象在y1=4x-12的图象的上方且这两个图象有交点,并且y3=ax2+bx+c的图象在y2=2x2-8x+6的图象的下方且这两个图象也有交点,不难画出三个函数图象有且只有一个交点(3,0)．做到这一步,得到了y3=ax2+bx+c图象上的第二个点的坐标．由点(-1,0),(3,0)在函数y3=ax2+bx+c的图象上,只能得到系数b、c与a之间的数量关系,即b=-2a,c=-3a,从而把函数y3=ax2+bx+c写成y3=ax2-2ax-3a,问题仍没有解决．

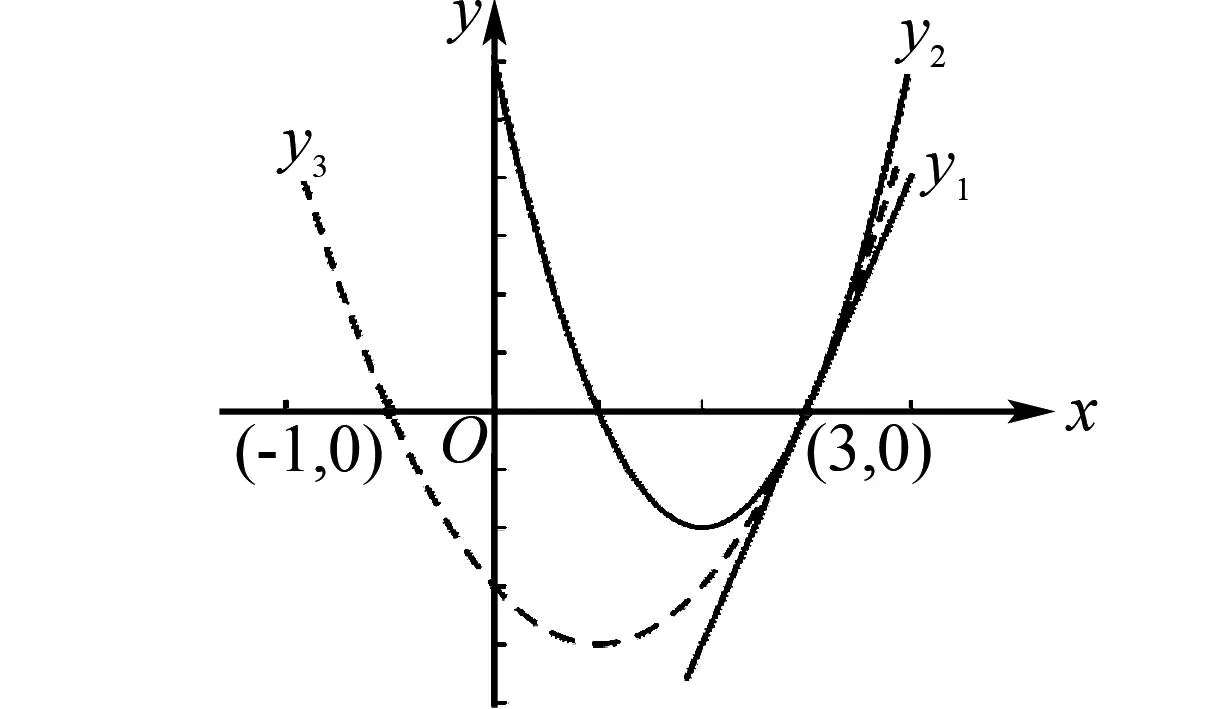
图1 问题(1)图

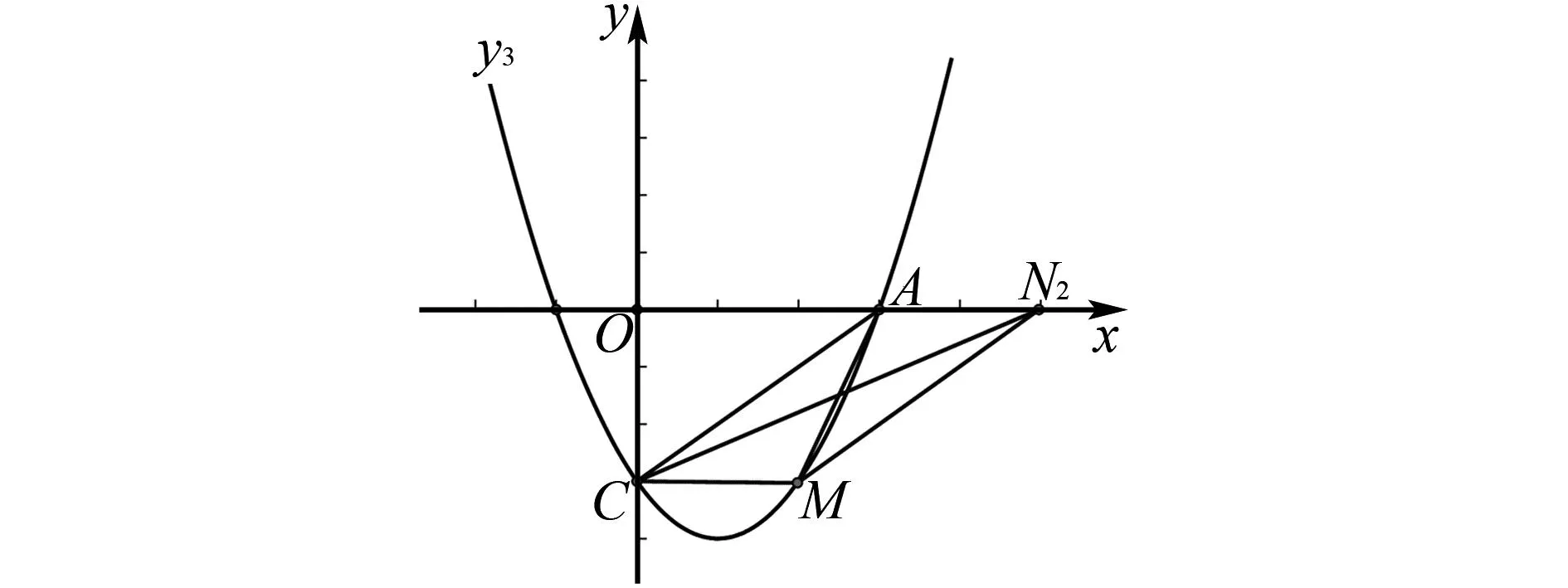
图2 点N在x轴正半轴且在在点A的左边,点M在x轴下方

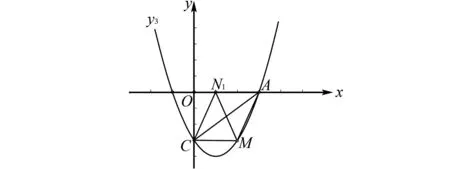
图3 点N在x轴正半轴且在点A 的右边,点M在x轴下方

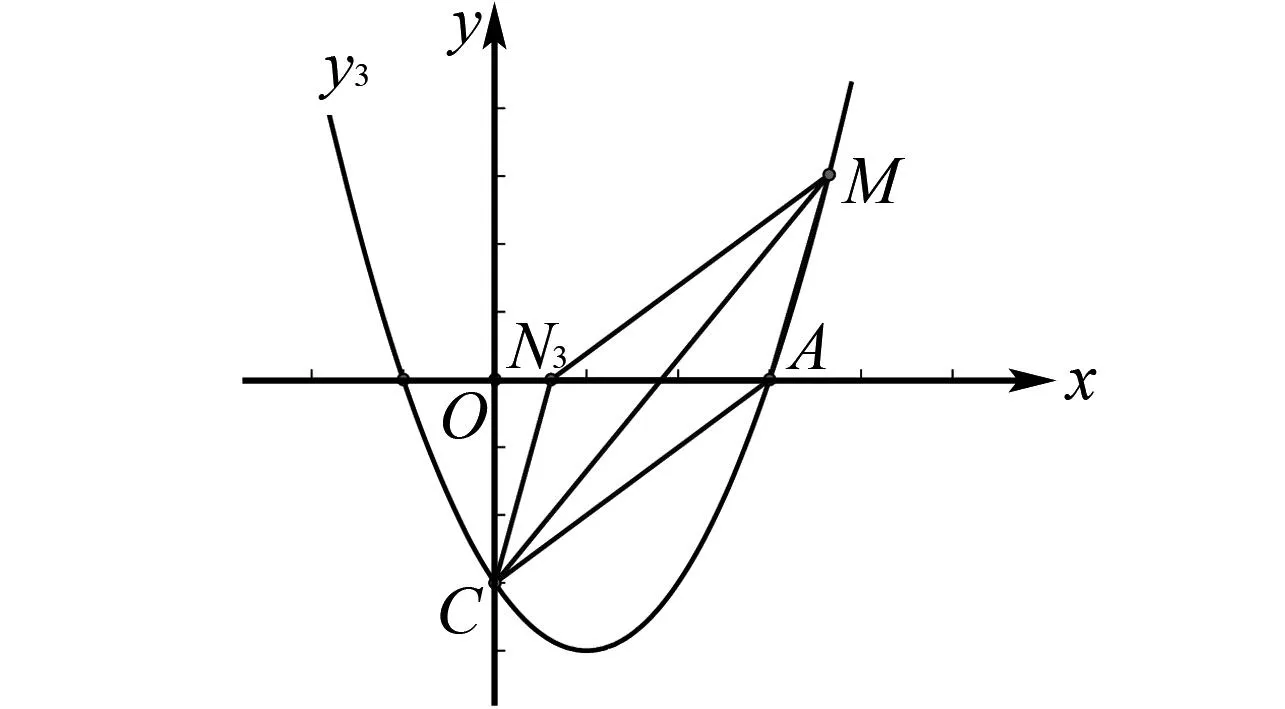
图4 点N在x轴正半轴且在在点A的右边,点M在x轴上方

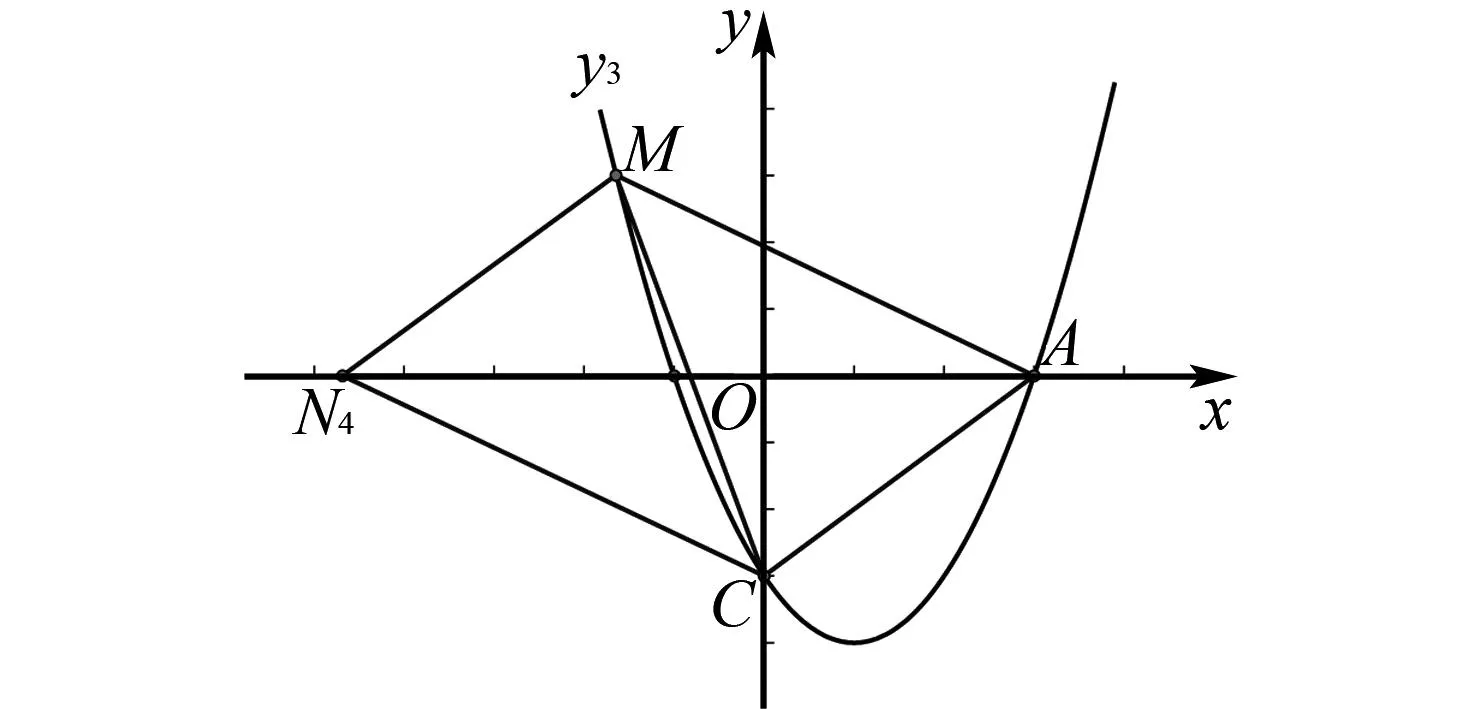
图5 点N在x轴负半轴,点M在x轴上方

难点之三:考查学生对于函数交点个数与方程根的个数之间的关系的理解,以及运用一元二次方程根的判别式判别方程实数根的情况．由函数y1=4x-12,y2=2x2-8x+6的图象只有一个交点(3,0),得到方程ax2-2ax-3a=4x-12,且这个方程只有一个解．再逆运用一元二次方程根的判别式b2-4ac=0,解得a=1,得出函数的解析式为y3=ax2+bx+c,问题才得以解决．

难点之四:问题(2)是一个常见的几何分类问题,难点在于如何合理制定分类的标准．理解平行四边形的判定方法,制定合理的分类标准,使问题解决不重不漏．

3 教学启示

3.1 完善数学知识体系,提升解题能力

在中考复习的课堂教学中,教师不仅要引导学生复习巩固函数基础知识、基本方法,更要唤起学生学习函数知识的经历,知道函数知识点在初中代数知识体系中所处的地位、作用以及与方程(组)、不等式等“点状”知识点之间的联系和区别,帮助他们构建初中代数知识体系．在教学中,教师为了让学生构建初中代数知识体系,可以借助知识框图、思维导图等可视化的思维方式引导学生,把所学知识点在知识体系中的位置清晰地呈现出来,使学生形成稳固的认知结构,力争让学生的初中代数知识、解题的思想方法融会贯通,进而培养学生解决综合问题的能力．

3.2 培养核心素养,理解核心知识

《义务教育数学课程标准(2022年版)》指出,数学素养是现代社会每一个公民应当具备的基本素养[1].数学课程要培养的学生核心素养主要包括以下三个方面:会用数学的眼光观察现实世界;会用数学的思维思考现实世界;会用数学的语言表达现实世界.核心素养具有整体性、一致性和阶段性,在不同阶段具有不同表现,小学阶段侧重对经验的感悟,初中阶段侧重对概念的理解.初中阶段,核心素养主要表现为:抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、应用意识、创新意识．

本题考查的初中数学核心知识有:一次函数、二次函数的图象与性质,函数与方程、不等式之间的联系,平行四边形的判定．

问题(1)通过“4x-12≤ax2+bx+c≤2x2-8x+6”这个连续不等式,联想到这是三个函数之间的数量关系,进而从抽象的数量关系,转化为直观的函数图象,研究三个函数的图象不难发现它都相交于同一个点(3,0),体现了对数学抽象、直观想象的考查．最后运用函数与方程的内在联系,根的判别式值为0的数学核心知识,需要学生解含有字母a的一元二次方程,体现了逻辑推理、数学运算的考查[2]．

问题(2)是近几年来数学中考命题的一个热点——动态几何题．点M是二次函数图象上的动点,导致以A、C、M、N为顶点的平行四边形的形状、位置不能确定,这时就要分类讨论．本题分类的依据是平行四边形的判定定理．学生在解题时能否想到分类讨论,取决于学生对相关概念、定义、定理的理解是否透彻,在日常的学习过程中,要经历分类讨论的过程,从而积累解决分类讨论问题的经验．因此教师要努力地使学生掌握分类思想方法,要求教师认真钻研教材,研究中考试题,有意识地为学生感悟分类思想创设问题情境、组织学习活动[3]．

4 结束语

完善数学知识体系和培养数学核心素养是相辅相成的．只有掌握了扎实的数学知识,才能更好地运用数学思维解决实际问题;只有具备了较高的数学核心素养,才能更好地理解和掌握数学知识．因此,教师在教学过程中应注重数学知识与核心素养的融合,为学生的发展打下坚实的基础．