基于直角坐标法的V-2RPa⊥R⊕2RSS 并联机构正逆解分析

邵国为

（常州纺织服装职业技术学院， 江苏常州 213016）

0 引言

近几年， 学者们对四自由度或五自由度并联机构进行了大量的结构综合研究，并确定了其运动的可行性。众所周知， 具有SchÖnflies 运动的机器人 （也称为SCARA运动或3T1R 运动）可用于各种工业任务，如取放、装配、包装和喷漆等。 但相对于三平移的Delta 机构[1-4]要更加的复杂，而相较于六自由度并联机器人，随着3T1R 型并联机构运动学等分析支链数的减少， 并联机构的工作空间增大，奇异构型减少。 因此有必要对3T1R 型并联机构进行理论研究。

Delta 并联机构构型综合后，相关学者对其位置求解问题展开了广泛的研究[5-7]。 已知Delta 型并联机构输入，求输出的问题的解决方法（正解）有两种：解析法和数字法。 Romdhane[8]采用解析方法，对一类3 自由度机构的正解进行了计算， 并得出了输入与输出之间的位置关系方程。 赵杰等[9]运用几何和向量代数的方法，实现Delta 机构运动学正解的快速、直观的推导，避免了并联机构运动学多正解选择的难题。 张利敏[10]对其进行了深入研究，并给出了相应的运动学模型。 对于一些较为复杂的并联机构，其正解通常是不能得到的，所以常用的算法是牛顿迭代算法，但是这些算法得到的结果并不包括全部的结果，选择起来也很麻烦。

在3T1R 并联机构的运动分析方面，Mahboubkhah[11]等提出了一种可用于加工的高刚度并联机构。 Wu 等[12]采用几何投影法，同时运用闭环矢量法对具有3T1R 运动的4PPa-2PaR 并联机构进行瞬时运动分析。Li 等[13]利用组态演绎法设计了一种创新的3T1R 并联机构，并对其位置进行了深入分析。 Zhang 等[14]提出了一种通用的解决方案，用于求解3T1R 过约束并联机构雅可比矩阵和约束海塞矩阵的统一公式。

本文提出一种基于方位特征集的V-2RPa⊥R⊕2RSS并联机构运动学分析设计方法。 在此基础上，利用一维搜寻法，构建一种只有1 个虚拟变量的方位一致性模型，基于直角坐标法， 从而方便地给出了该正解的一个解析式，并给出了逆解求解结果来证明该正解的正确性。这为优化并联机构的参数以及研发原型机提供了一些理论支持。

1 机构结构分析

1.1 机构描述

参照图1，该机械装置包含了一个运动平台1 （位于图1 底部方框内） ，一个静止平台0，两个RSS 支臂和两个V 型方位布置的混合支臂V-2RPa⊥R。 两个混合支臂均是由四个球状（球副）连接点（Sa，Sb，Sc，Sd）形成的一个平行四边形组成，我们称之为Pa 部分（即“parallel”）。

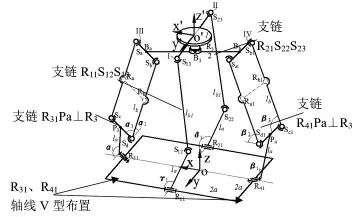
图1 V-2RPa⊥R⊕2RSS 并联机构及位置求解模型

两个由（Ra、Rb）的组成的杆安装在Pa 部件中平行四边形结构中间位置，平台1 上R3的轴必须与静平台0 垂直，从而得到3T1R 输出的混合支链V-2RPa⊥R。 静止平台0 上的4 个驱动副R11｜｜R21、R31⊥R41，其中，R31与R41呈V 型布置。 动平台1 能够进行三移动和绕R3 轴线旋转（3T1R）运动。

1.2 计算耦合度κ

（1）确定混合支链HSOC1及其约束度△1。

由文献[15]，HSOC1有两种选择方案：

①若选V-2RPa⊥R 支链构成HSOC1，即

HSOC1{R31｜｜P（4s）-P（4s）-R（4s）-P（4s）-P（4s）-R（4s）｜｜R41⊥R3-S13-S12-R11-}

由文献[15]有

②若2RSS 构成SOC1，即

SOC1{-R11-S12-S13-S23-S22-R21-}

则

应选择方案①

（2）确定及其约束度

SOC2由支链R21S22S23组成，即

SOC2{-S23-S22-R21-}

由式（1）有

（3）由此可得

结构只包含一个BKC，其耦合程度为1，能够获得所有的数值解[15]。

2 位置分析

2.1 位置正解分析

2.1.1 坐标系建立及符号标注

V-2RPa⊥R⊕2RSS 并联机构的正解问题可表示为：给定主动杆的输入参数α1，β1，γ1，δ1， 求解末端执行件1（动平台1）的输出参数（x，y，z）（三平移）和γ（一转动）。

如图1 所示， 直角坐标系统O-XYZ 的OX 与OY 轴均位于静态台的中心位置，该系统的X 轴、Y 轴及Z 轴分别对应于一条固定的线段，且通过使用右手定律来定义Z 轴。动坐标系统O'-X'Y'Z'的原点设在了S13S23的中部，当动平台开始移动时，X'轴、Y'轴和Z'轴沿着相应的方向运动。

图2 为V-2RPa⊥R⊕2RSS 机构展开图，静态平台长度设定为2a，宽度2b，而（末端执行平台）动态平台1 是一个等腰直角三角形，其边长为2m2。

图2 V-2RPa⊥R⊕2RSS 并联机构展开图

动平台1 围绕旋转副R3的旋转角度是动平台1 的输出姿态角γ，可表示为S13O'与OX 轴的所夹锐角，逆时针取正。

设定R3与B3的连接长度为q1，Ba与Bb连接长度为l，初始位置时，Ba和Bb的连线与Sa和Sb的连线、Sa1和Sb1的连线的夹角均为φ，此时设定R11与S12的连线，R21与S22的连线长度均为la1，S12与S13的连线长度、S22与S23的连线长度均为lb1；R31与P3的连线长度、R41与P4的连线长度均为la，P3与Ba的连线长度、P4与Bb的连线长度均为lb。

根据图1 和图3，Ш 和Ⅳ分支的输入角分别为R31与P3的连线（la）与XOY 平面的夹角（α1）以及R41与P4的连线（lb）与XOY 平面的夹角 （β1）， 两个Pa 部分的平面分别与XOY 平面之间的夹角分别是α2，β2，Pa 部分的内夹角锐角分别为α3，β3，设定逆时针方向为正。

图3 III 支链与IV 支链的运动位置模型

I、 II 分支的主动输入角度是γ1，δ1，以相对于静坐标系OXY 的X、Y、Z轴线的角度来代表连接杆S13S12、S23S22在空间中的位置； 也就是γ2，γ3，γ4以及γ5，γ6，γ7的角度，见图4。

图4 I、II 支链计算模型

2.1.2 基于SOC 的位置建模分析

2.1.2.1 在△1＞0 的条件下对HSOC1的运动位置建模

（1）由HSOC1（III、IV）支链，分别可得O’坐标值

由式（1）、（2）可得，

β3为中间值，可以消除，首先令

从而得到

解方程可得：

（2）由第一条支链（I 支链），得到R11S12S13支链上球副S12、S13点的坐标为：

进一步，由S12与S13两点之间的长度等于lb1，有

A1sinγ+B1cosγ+C1=0其中，

令

解之有：

得到输出角（γ*）的函数表达式，同样也是一个关于α3*的函数

即γ*=f2（α3*）

2.1.2.2 在△2＜0 条件下的SOC2支链运动位置数学模型

由II 支链，得R21S22S23支链中的球副S22、S23点坐标为：

进一步，由S22与S23两点之间连线的长度等于S12与S13两点之间连线的长度，均为，建立其支链II 的位置方程，即

设定变量α3*在（0°，360°）范围内改变数值，在满足f（）=0 的情况下，即可求解对应α3的数值解，由式（2）、（4）、（5）即可求得动平台位置解o'（x，y，z）；代入式（7），即可求得动平台绕Z 轴旋转角度γ。

2.2 位置反解求解

V-2RPa⊥R⊕2RSS 并联机构的反解问题可描述为：给定动平台1（末端执行器）的位置、姿态参数（x，y，z）（三平移）和γ（一转动），求解主动杆相对于XOY 平面的输入角度参数α1，β1，γ1，δ1。

2.2.1 基于直角坐标法求V-2RPa⊥R⊕2RSS 机构中各位置坐标

由2.1.2 可知，

Ba点在静坐标下矢量方程

Ba点在静坐标下矢量方程

则S13的绝对坐标为：

即

同理可得R21S22S23支链中的球副S23的在静平台坐标系O-XYZ 下的坐标为：

2.2.2 建立位置方程

根据连杆约束条件可得：

2.2.3 求输入角α1，β1，γ1，δ1

由（14）式可得R31Pa⊥R3支链主动输入角α1：

其中，A1=2（z-q1）la

由式（15）可得R41Pa⊥R3支链主动输入角β1：

其中，A2=2（z-q1）la

由式（16）可得R11S12S13支链主动输入角γ1：

其中，A3=-2zla

由式（17）可得R21S22S23支链主动输入角δ1：

其中，A4=-2zla

当输出参数和已知时，α1，β1，γ1，δ1分别有两组解。 故位置逆解数为2×2×2×2=16， 因此，V-2RPa⊥R⊕2RSS 并联机构动平台可输出有16 种构型。

2.3 实例验算

2.3.1 正解算例

因V-2RPa⊥R⊕2RSS 机构与H4（I4R）均含有Pa 复杂支链，为便于后续性能对比，取与产业用H4 并联机构相同的尺寸，即，

令相应杆长尺寸数据为：la=375，lb=800，la1=375，lb1=880，a=400，b=400，m2=200； 其余还参数包括：l=350mm，q1=40mm，φ=45°。 对主动杆输入角进行赋值，

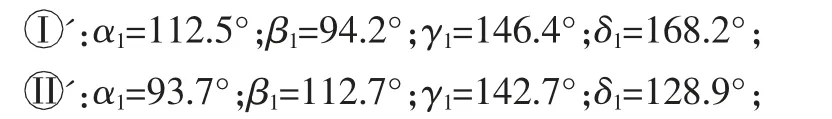
依据式（1）～式（9），通过使用一维搜寻方法[15]，可以从两组角度中得到V-2RPa⊥R⊕2RSS 机构末端执行器的四个位置，如表1 所示。

表1 V-2RPa⊥R⊕2RSS 并联机构的末端位置

2.3.2 逆解算例

3 样机CAD 建模

图5 展示了V-2RPa⊥R⊕2RSS 并联机构的虚拟样品设计总图，其中包括静态平台0、动态平台1、动态平台2、RSS 支链3、复杂支链（含Pa）4 和驱动系统5 这六个主要部分。

图5 V-2RPa⊥R⊕2RSS 并联机构的虚拟样机图

3.1 支链设计

V-2RPa⊥R⊕2RSS 并联机构由四条支链并联耦合而成， 为动平台传递运动、末端执行件承受载荷，支链的结构须在满足工况的前提下，质量尽量轻。 因此，四个支链中的主动臂和从动臂都使用了碳纤维编织管状结构， 这种结构具有轻量化、高强度和高模型等优点。RSS 支链与复杂支链（含Pa）的3D 结构如图6 所示。

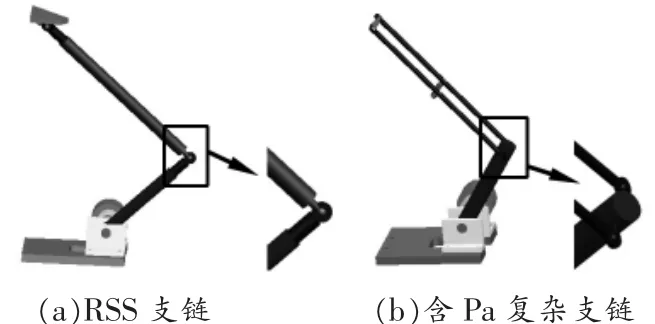
图6 支链结构图

3.2 动、静平台的设计

子动平台1和子动平台2是相互垂直并且通过转动副连接，进而实现V-2RPa⊥R⊕2RSS 并联机构末端的绕Z 轴的旋转运动，同时通过球关节（S13 或S23）分别连接两个RSS 支链，从而构成了可实现三平移一转动输出运动的V-2RPa⊥R⊕2RSS 机构的结构。同时，该并联机构的静平台0 安装有4 块电机安装板，4 台伺服电机，结构如图7 所示。

图7 静平台结构设计

4 结论

提出了一种四自由度V-2RPa⊥R⊕2RSS 并联机构， 结构比H4、I4R 机构更为简单、动平台装配结构更为容易。

利用一维搜索计算出了V-2RPa⊥R⊕2RSS 并联机构的耦合度，并得到四组机构末端位置数值解。进一步求解后，我们得出了机构位置反解的解析式。

这个结构设计简洁，为后期的动力学分析奠定了基础。